一種改進的多領導鯨魚優化算法

余賢星

(上海理工大學機械工程學院，上海 200093)

yvxianxing@163.com

1 引言(Introduction)

鯨魚優化算法的優越性有目共睹，因此該算法在優化問題上應用廣泛。但其存在收斂速度慢、收斂精度低、搜索能力不足的缺點，各種改進的鯨魚算法應運而生。其中改進方式有將兩種算法的優勢結合而成，也有通過其他策略。ZHANG等提出了一種基于聚集策略的混合鯨魚優化算法，將鯨魚優化算法和灰狼優化算法優勢結合。林杰等提出了一種基于混沌的正余弦鯨魚優化算法，加快了算法的收斂速度，避免了早熟，平衡了搜索與開發。郭啟程等提出了一種基于萊維飛行的鯨魚優化算法，用于解決無人機三維路徑規劃問題。董明明等為了解決現有輥道窯窯溫異常檢測存在的各種問題，提出了一種采用自適應反向學習策略和高斯變異算子的改進鯨魚優化算法。劉紫娟等提出了一種改進的離散鯨魚優化算法，用于應對復雜網絡社區發現的應用場景。朱誠提出了一種引用雙非線性收斂因子和強制驅散機制改進的鯨魚優化算法，能夠有效簡化路徑復雜度、降低機器人控制難度。

本文提出了一種改進的多領導鯨魚優化算法，該算法引入了多領導機制和萊維飛行機制。多領導機制是將初始種群均分為四個小種群，每個種群根據各自種群的最優位置進行迭代更新。每10 次迭代進行一次種群重組，有利于提高種群的多樣性，避免整個搜索過程陷入局部最優。萊維飛行機制是將每代的最優位置進行隨機擾動，有利于加快收斂，避免陷入局部最優。通過標準方程和現實生活問題進行驗證，表明了該算法的優越性。

2 鯨魚優化算法(Whale optimization algorithm)

2.1 圍捕獵物

座頭鯨能夠感知獵物的位置并發動攻擊。在一個最優位置不確定的搜索空間里，假設所有座頭鯨的最佳位置就是最優或者在最優位置旁邊。那么一旦確定最優的座頭鯨位置，其他鯨魚就會根據最優更新。更新公式如下：

2.2 泡泡網攻擊方式

座頭鯨沿著曲率半徑越來越小的螺旋線路徑向上游動，通過吐泡泡的方式，形成一堵氣墻，將獵物圍在一起最后捕殺。泡泡網攻擊模型中包含兩種方式：一種是收縮環繞，通過遞減的值，影響的范圍；另一種是螺旋更新，位置更新公式如下：

由于兩種更新方式同時發生，因此添加一個概率數，來決定具體使用哪一種更新方式。

2.3 搜尋獵物

收縮環繞更新中，目標鯨魚可能是最優位置鯨魚，這就是進行開發階段；也可能是其他任意鯨魚，這就是搜索階段。當進行到搜索階段時，鯨魚位置更新公式如下：

2.4 鯨魚算法的更新方式總結

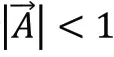
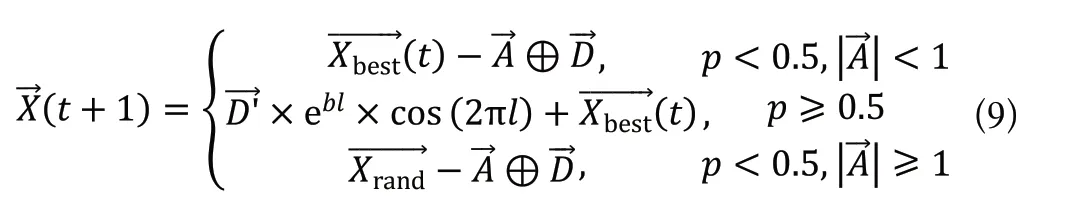
3 改進的鯨魚算法(Improved whale optimization algorithm)

3.1 多領導機制

該算法中引入多領導機制是為了提高種群的多樣性，避免搜索個體陷入局部最優。如圖1所示，初始化一個種群，將其均分為4 個小種群，每個種群對應各自的最優個體位置，每次迭代都根據各自種群的最優位置進行更新。每10 次迭代結束，就會進行一次種群間的信息交流，就是將各種群內的個體進行一次打亂重組，有利于擴大搜索范圍，避免陷入局部最優。

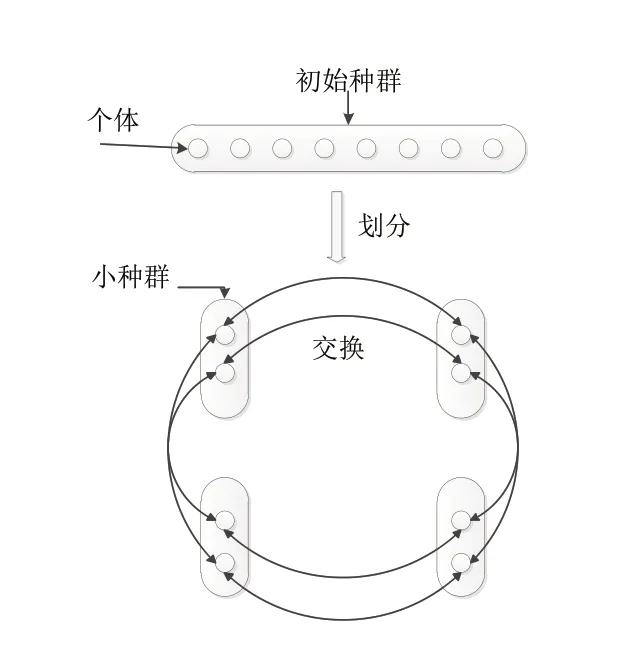
圖1 多種群機制Fig.1 Multi-population mechanism

3.2 萊維飛行機制

該算法引入了萊維飛行機制，為了將最優位置進行隨機擾動，加快收斂速度，避免陷入局部最優。更新公式如下：

其中，Γ 是Gamma函數。

3.3 算法流程

算法IWOA偽代碼如下所示。

4 標準方程測試(Benchmark functions test)

4.1 試驗設置

CEC2014標準函數是測試算法性能的重要實例。從中選取6 個標準函數，詳見表1，其中、、是單峰函數，、、是多峰函數。單峰函數只有一個全局最優解而沒有局部最優解，用來測試算法的開發性能，得到的最優解精度越高，表明算法具有更優的開發性能。多峰函數只有一個全局最優解卻含有多個局部最優解，而且隨著函數維度升高，優化復雜度越高，用來測試算法的搜索能力和開發能力。對于搜索能力不足的算法，在優化多峰函數時容易陷入局部最優。將該算法與其他先進的算法比較，其中包括粒子群算法(PSO)、灰狼優化算法(GWO)、鯨魚優化算法(WOA)、混合鯨魚灰狼優化算法(HWOAG)、提升的鯨魚優化算法(WOAmM)。對于這些算法中的參數設置，詳見表2。

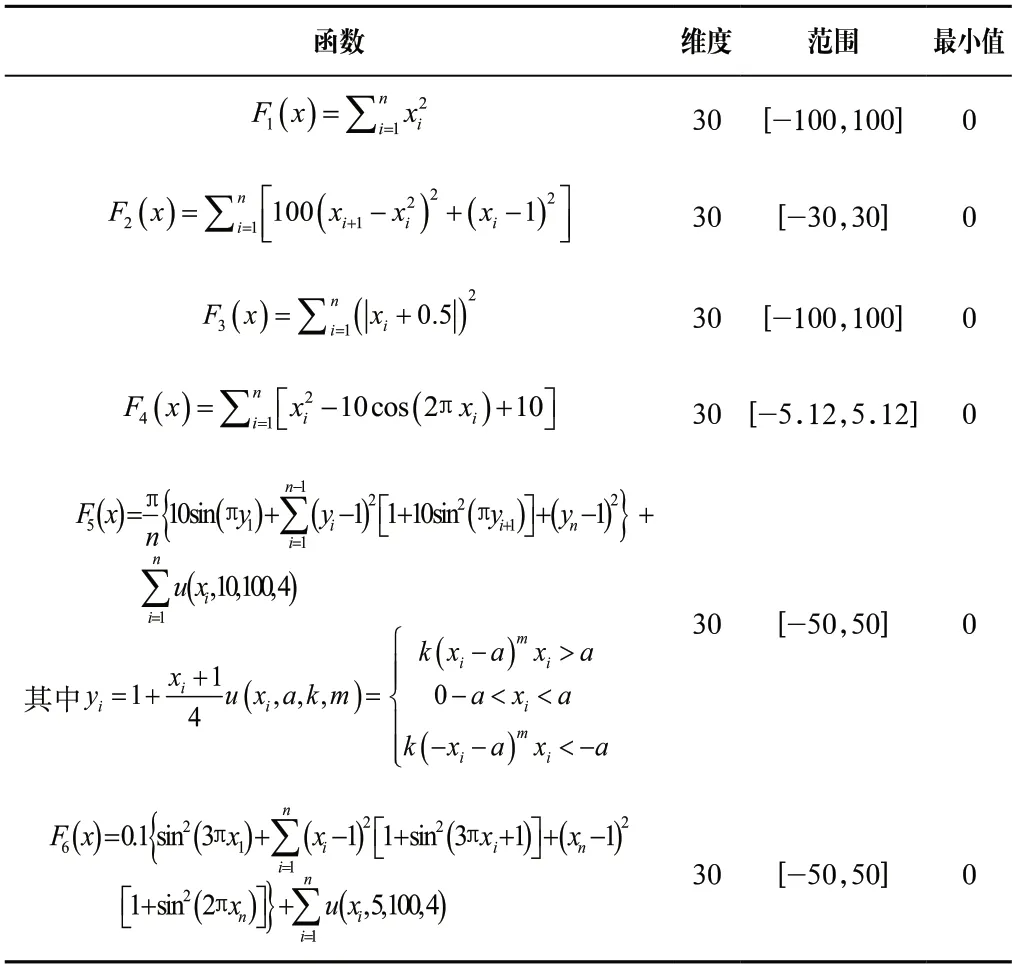
表1 6 個標準函數Tab.1 Six benchmark functions

表2 算法參數Tab.2 Algorithms parameters

4.2 測試結果

將所有的算法在32 個個體、500 次迭代次數、30 次運行次數的情況下，對30 維的標準函數進行測試，統計最優解的平均值和標準方差。平均值能夠直觀展示算法的效果，而標準方差能夠判斷算法的穩定性。優化結果對比詳見表3。

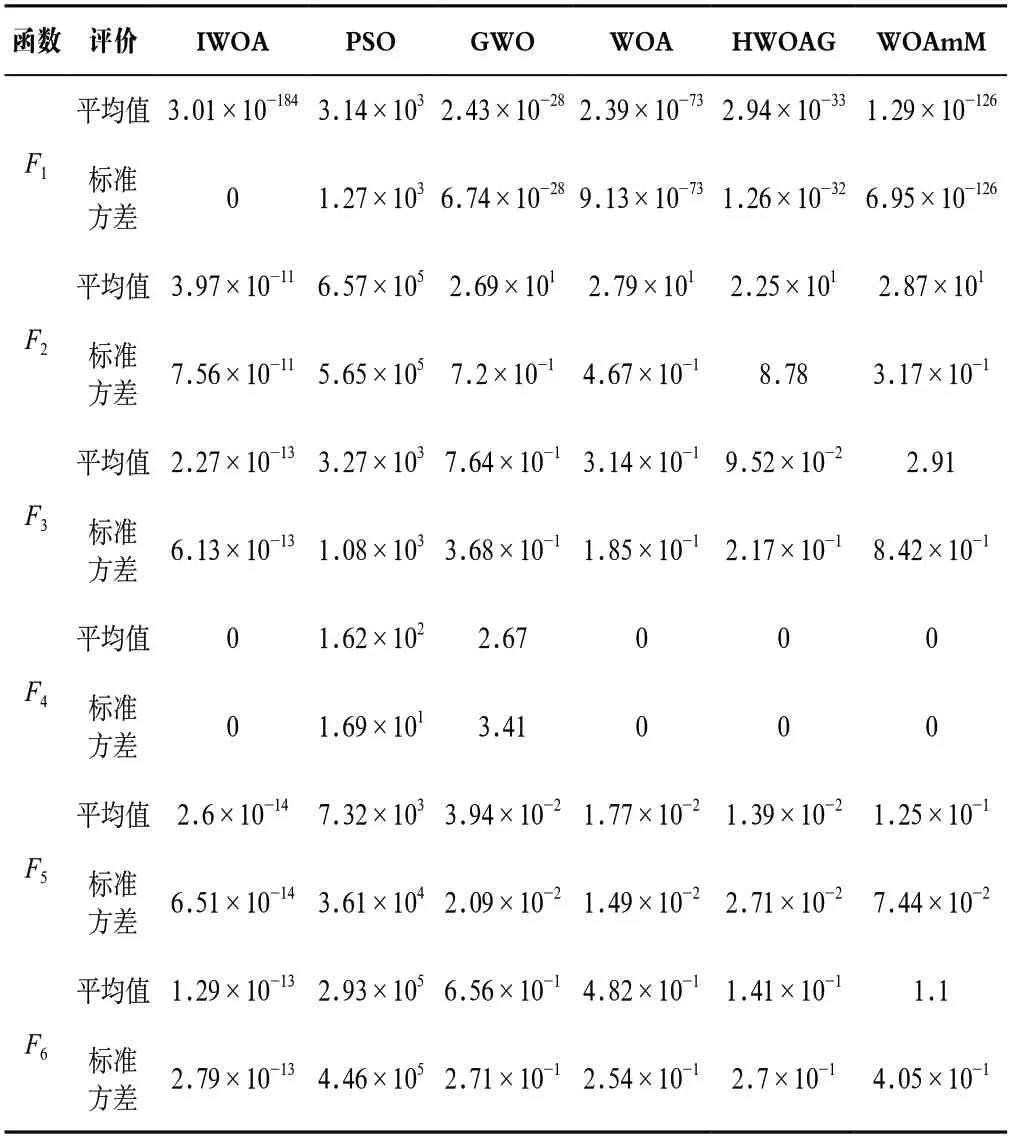
表3 6 個函數的對比結果(32 個個體，30 維)Tab.3 Comparison results of 6 benchmark functions(N=32，D=30)

從統計數據可以看出，在6 個測試函數中，相比于其他5個算法，該算法的優化結果最小。從平均值可以看出，該算法相比于其他幾個算法，收斂精度更高，而且在上取得了最小值0。從標準方差可以看出，該算法具有高穩定性。

4.3 收斂分析

收斂性是算法的一個重要衡量標準，收斂速度越快，算法效率越高。如圖2所示，對于單峰函數，所有算法都能快速收斂，相比于其他幾個算法，該算法具有很強的后期開發能力，最優解的精度高。對于多峰函數，該算法在迭代前期收斂比較慢，大部分個體用于搜索，接著就會有一個加速收斂的過程，算法對可能性大的區域進行搜索，這時候算法已經確定了最優解的大概位置，因此搜索個體會在最優位置周圍進行開發，最后收斂曲線放緩。而其他算法剛開始就快速收斂，當進行到搜索中后期的時候，最優解一直不變，停滯不前，此時算法已經陷入局部最優。其他算法開發能力不強，即使找到可能性大的區域，得到的最優解精度也不夠。如圖3所示，箱線圖也表明了算法的求解精度高而且穩定。

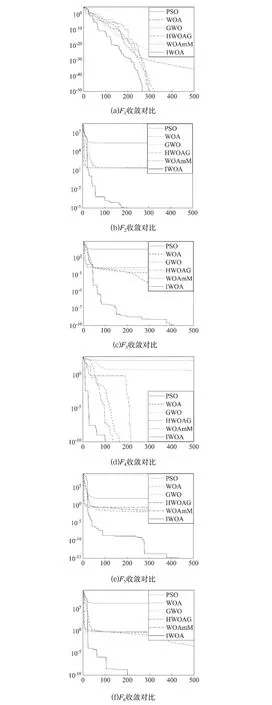
圖2 不同函數收斂曲線圖Fig.2 Convergence line graphs of different functions

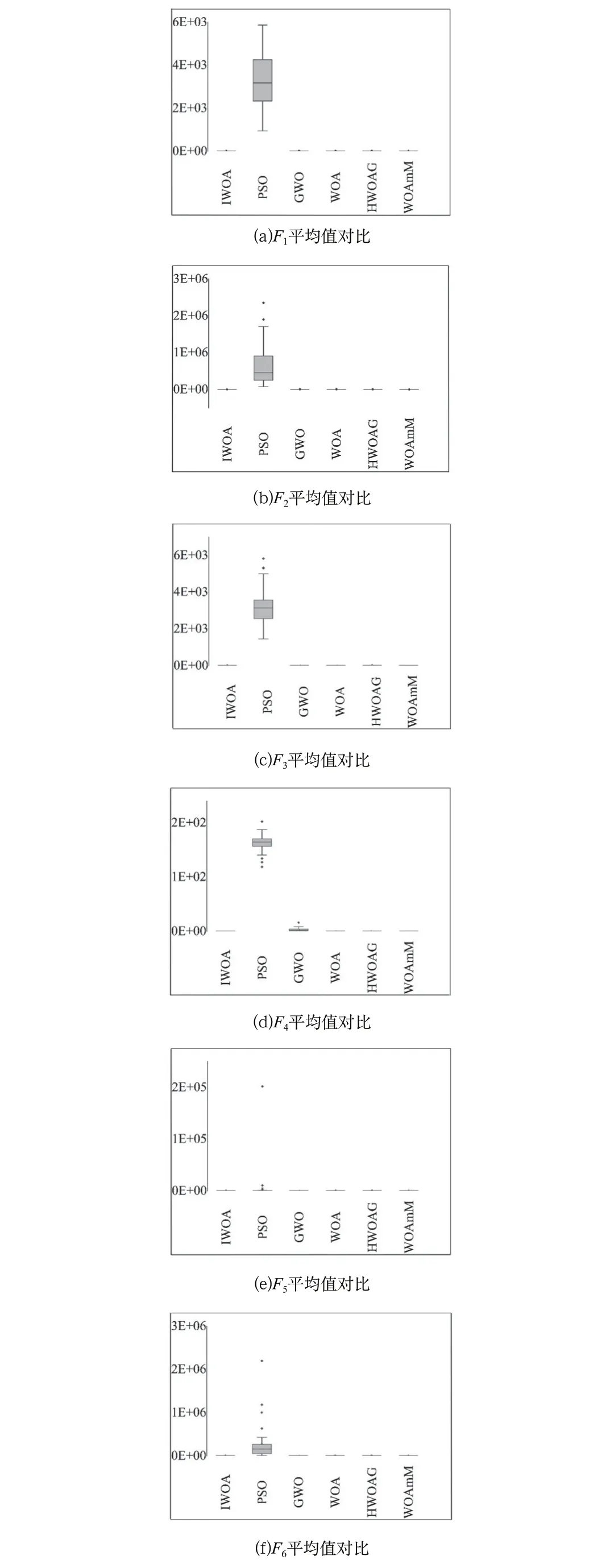
圖3 不同函數箱線圖Fig.3 Boxplots of different functions

5 工程優化問題測試(Engineering optimization problems test)

現實生活中有許多經典的多變量工程問題，被許多學者作為優化算法的測試實例。本文選取了三個約束問題，通過改進的多領導鯨魚優化算法進行優化，并與其他算法進行比較，其中部分優化結果來源于提升的鯨魚優化算法。以下是這三個問題的描述。

5.1 懸臂梁的設計問題

懸臂梁由五個等厚的空心方塊組成。梁在第一塊上有剛性支撐，在第五塊的自由端有一個垂直力作用。懸臂梁結構示意圖如圖4所示。這個問題需要最小化懸臂梁的重量，并且滿足開口端垂直位移上限的約束要求。、、、、(mm)分別表示五個空心方塊的長度。目標方程、約束條件和變量范圍如下。

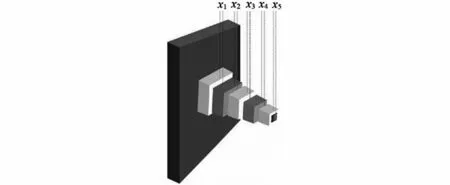
圖4 懸臂梁結構示意圖Fig.4 Cantilever beam structure figure

目標函數：

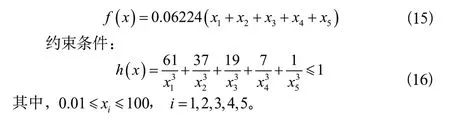
從表4中可以得出，在懸臂梁的設計問題中，該算法得到了最小值1.3365。相比于其他算法，值都略優。從結果可以看出，該算法的求解精度高，在最優值周圍區域，開發精度很高。雖然其他算法也得到了近似值，但由于其他算法精度不高，因此略顯劣勢。

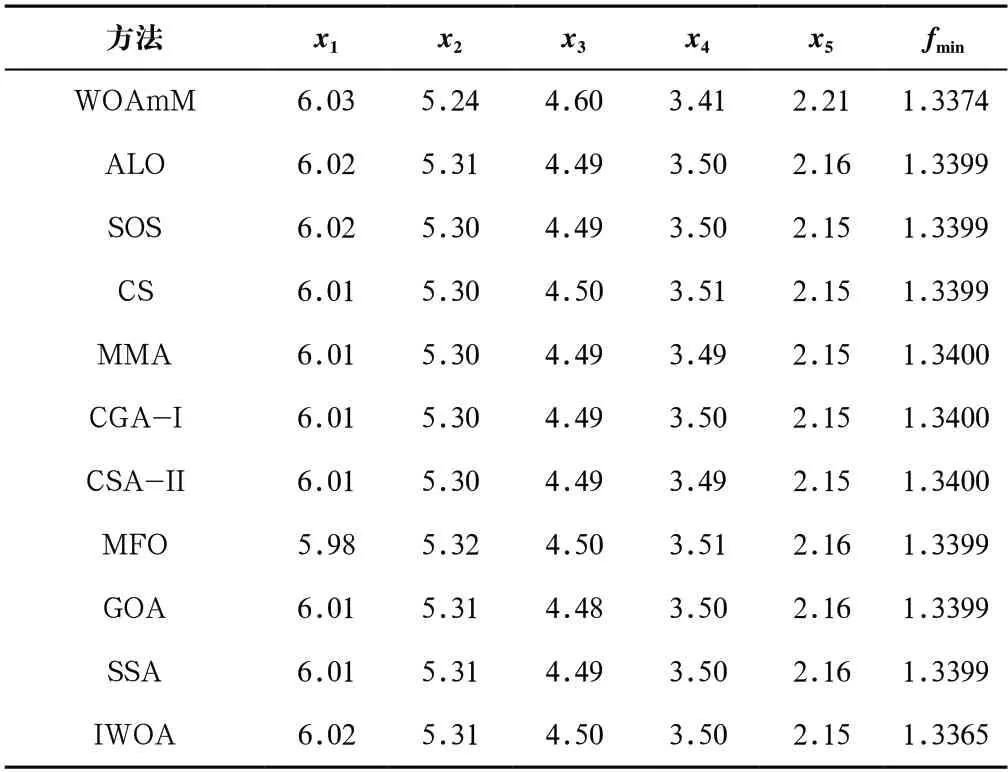
表4 懸臂梁設計問題的結果對比Tab.4 Comparison of results on cantilever beam design problem

5.2 三桿桁架設計問題

如圖5所示的三桿結構和受力情況下，在滿足彎曲、撓度、應力時最小化三桿桁架的體積，這個問題就是通過兩個變量、(cm)調整橫截面積。目標方程、約束條件和變量范圍如下。

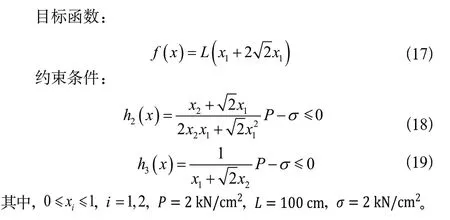
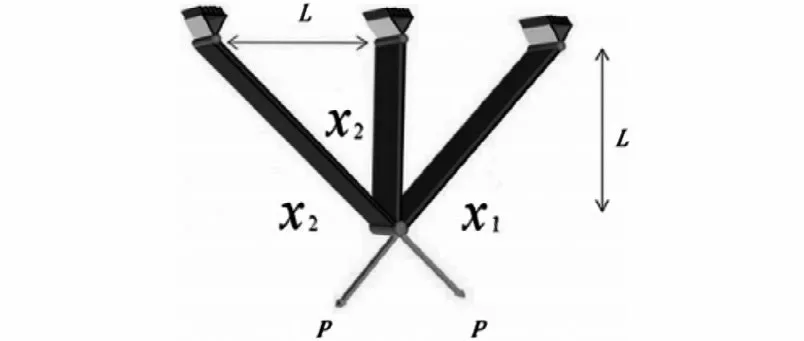
圖5 三桿桁架結構和受力示意圖Fig.5 Three-bar truss structure and force figure

從表5中可以看出，所有算法都得到了相同值，除了Ray&Sain，因此，在這個具有兩個變量的問題中，所有算法都到了最優值。說明了該算法在提升搜索能力的同時，也具有很強的開發能力。

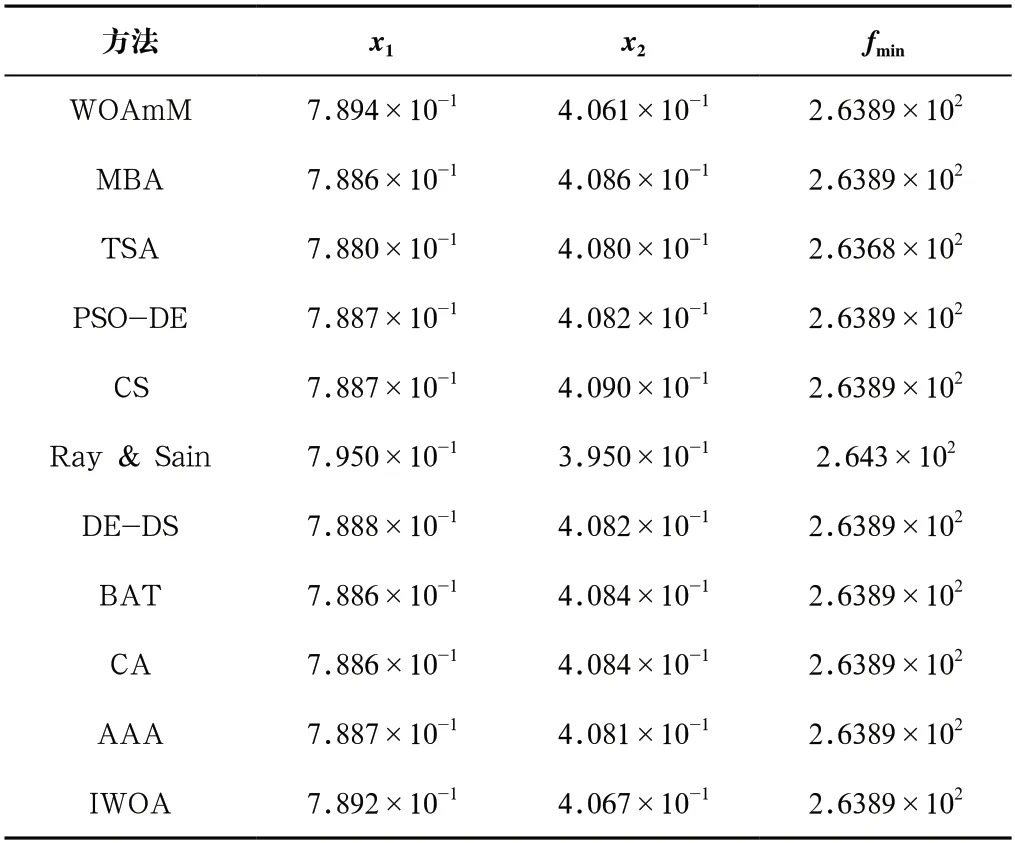
表5 三桿桁架設計問題的結果對比Tab.5 Comparison of results on the three-bar truss design problem

5.3 輸氣壓縮機設計問題

這是一個具有四個變量的機械設計問題，目標是確定變量的值，以便使用最低成本能每天傳輸1億立方米的天然氣系統。其中一個變量是壓縮機站的距離(m)，第二個是壓縮機的效率，第三個是管道的直徑(cm)，第四個是管道的速率(m/s)。目標方程、約束條件和變量范圍如下。

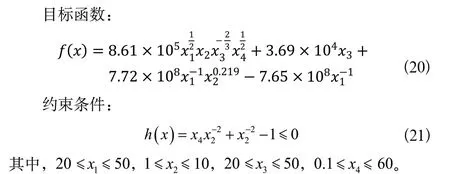
從表6中可以看出，該算法得到了最小值，且遠優于其他算法。該算法在搜索能力上有很大的提升，能避免陷入局部最優，很大提升了算法的優越性。其他算法都得到了近似值，說明其他算法陷入了局部最優解。而改進的多領導算法，因為萊維飛行和多領導機制，直接使算法跳出局部最優，向更優區域進行搜索開發。

表6 輸氣壓縮機設計問題的結果對比Tab.6 Comparison of results on gas transmission compressor design problem

6 結論(Conclusion)

本文提出了一種改進的多領導鯨魚優化算法。該算法引入了多領導機制，有利于提高種群的多樣性，防止陷入局部最優；引入萊維飛行機制，將最優個體進行隨機擾動，加快收斂速度，防止陷入局部最優。通過6 個標準函數進行測試，從平均值和標準方差可以看出，該算法在收斂精度和穩定性上，相比于其他算法有很大優越性。從收斂圖可以看出，該算法收斂速度快，收斂精度高。同樣在箱線圖中可以看出，該算法準確性高，無論是單峰函數還是多峰函數，都能準確判斷最優位置區域，并在最優位置周圍開發。通過三個工程優化實例進行驗證，該算法都能得到最優值。后續可以將該算法運用到其他機械設計問題中。