一種適用于間接學習結構的功率放大器線性化算法

張紅升 易勝宏 馬小東 衛中陽 楊虹

（重慶郵電大學光電工程學院,重慶 400065）

引 言

功率放大器(以下簡稱功放)作為數字通信系統中功耗最大的關鍵部分，其性能和特點備受學者們的關注與研究.作為典型的非線性器件，高性能功放容易產生電效應與熱效應[1]，從而導致其特有的記憶效應與非線性效應，當調制好的基帶信號具有較高的峰均比(peak to average power ratio,PAPR)和較大的帶寬時，這些效應會影響功放輸出信號的幅值和相位，產生更為嚴重的信號失真，體現在頻域上為諧波失真與交調失真，體現在時域上則是幅度失真與相位失真.由于這種失真的主要頻段距離主信道頻段很近，很難通過設計一個良好的帶通濾波器進行濾除[2]，所以包括功率回退法、模擬預失真法和數字預失真法等各種解決或減少功放失真的方法被提出，并已被廣泛應用在數字通信系統中.數字預失真的原理是，系統輸入的數字基帶信號經過一系列的非線性變換，達到與基帶信號通過功放后的輸出信號相反的幅度-相位特性.這一系列非線性變換實際上是對基帶信號的增益補償與相位對齊操作，稱為預失真，其原理如圖1 所示.x(n)為基帶信號，y(n)為經預失真處理后的信號.z(n)為功放輸出信號.可以看出，經過預失真處理后的輸入-輸出特性曲線是線性的，提高了功放的效率.

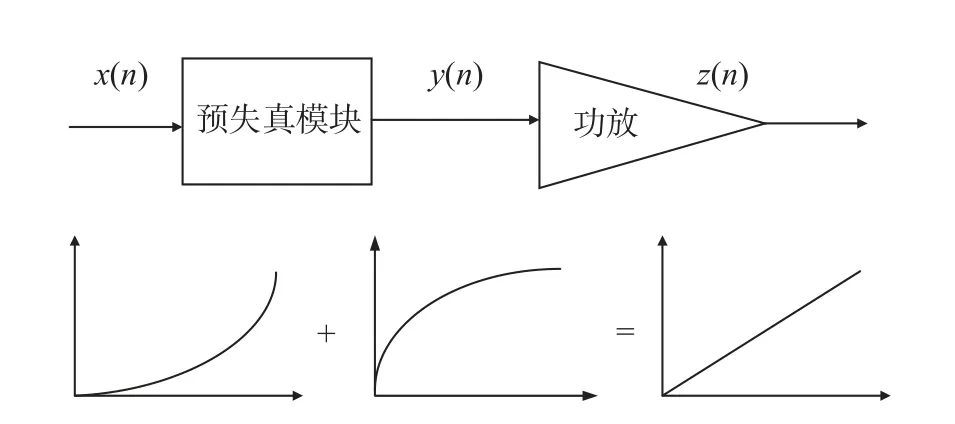
圖1 預失真原理圖Fig.1 Principles diagram of pre-distortion

近年來，為了提高預失真系統的穩定性和魯棒性，不斷有學者提出各種新的預失真系統結構，其中包括直接學習結構(direct learning architecture,DLA)、間接學習結構(indirect learning architecture,ILA)和直接識別結構(direct cognitive architecture,DCA)，其中，DLA 將代價函數(誤差)定義為原始輸入信號和輸出信號之差，再通過自適應訓練模塊使得輸出信號朝著純凈的輸入信號擬合，直至誤差最小化[3-4].其原理圖如圖2 所示.

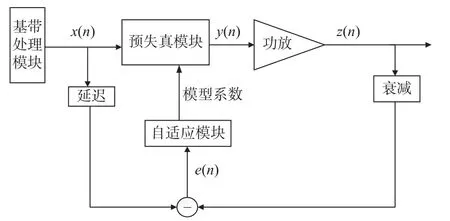
圖2 DLA 原理圖Fig.2 Principles diagram of DLA

ILA 是一種基于功放后置逆的學習結構[5]，其通過后失真模塊與預失真模塊之間的輸出誤差調節兩個模塊的參數.該結構可以直接使用全局最優擬合算法，比如最小二乘 (least aquare,LS)算法，擬合出預失真狀態最佳、輸出信號失真最小時的后失真與預失真系數，并迭代至后失真與預失真模塊中實現預失真操作，由于功放的非線性特性是緩慢變化的，故本系統不需要實時更新模型系數，降低了對硬件的要求，提升了系統穩定性，直接實現了開環預失真結構.其原理如圖3 所示.

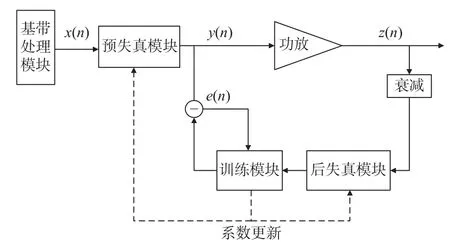
圖3 ILA 原理圖Fig.3 Principles diagram of ILA

為提高帶外抑制效果且簡化系統，馬岳林提出了直接識別與求逆結構(direct cognitive and inverse architecture,DCIA)[6]，其通過直接識別模塊，利用LS 算法，求出預失真模塊與功放數字模型相匹配的模型系數.該結構通過功放的輸入y(n)與 輸出z(n)，計算與功放輸出擬合度最佳時的模型參數，然后將參數復制給模型求逆模塊計算功放的逆模型參數.其原理圖如圖4.

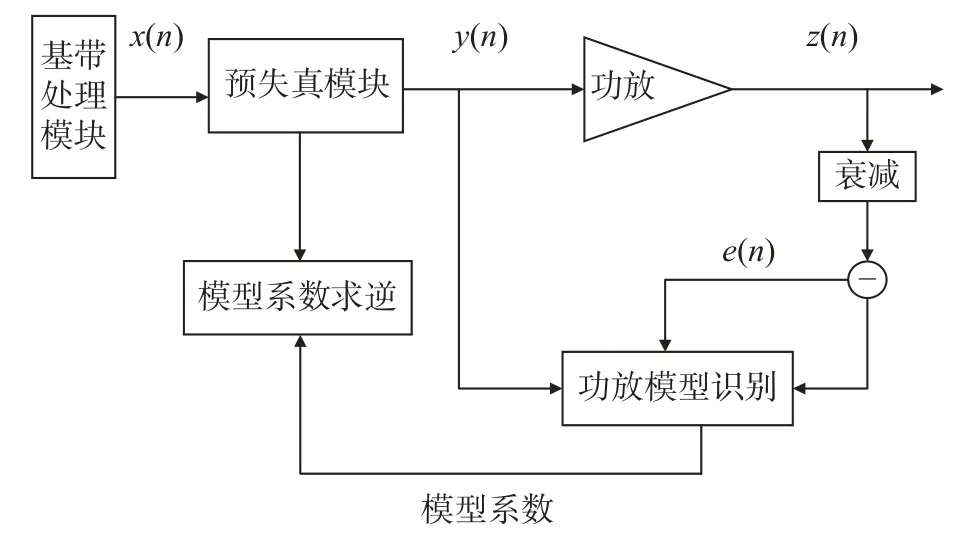
圖4 DCIA 原理圖Fig.4 Principles diagram of DCIA

本文通過對傳統的ILA 預失真進行改進，增加一個功率統計模塊，提出了一種基于ILA 的交叉信號訓練預失真算法.該算法將功放的輸出信號反饋至信號截取與功能功率計算模塊，該模塊實質上是一種可滑動的窗函數，截取輸入信號流并計算其功率之和，通過設置窗函數的長度N，可以計算出流動數據的平均功率.本文中，預失真與后失真模型均采用記憶多項式(memory polynomial,MP)模型實現對功放的行為擬合，新提出的算法將系統的反饋信號中大功率信號流與隨機信號流分別傳送進后失真模塊中進行數據處理，隨后將后失真模塊處理后的數據與預失真模塊處理后的數據同時送入自適應算法模塊中，通過LS 算法計算系統的預失真參數并分別分配到后失真與預失真模塊中，實現功放的線性化.本文采用PAPR 為9 dB 的LTE 信號通過在線測試平臺RF WebLab 對真實GaN 功放進行仿真[7]，與目前現有的順序數據流處理算法與大功率數據流處理算法相比，本文提出的交叉信號訓練預失真算法在信號主頻帶外的失真頻段優化了5 dB 左右，同時，基于大功率和隨機訓練交叉訓練算法的歸一化均方誤差(normalized mean square error,NMSE)分別比順序數據流處理算法與大功率數據流處理算法的NMSE小約1 dB 與0.6 dB，且迭代后的NMSE 均小于-23 dB.

1 預失真結構及算法創新

數字預失真系統的研究主要包括功放數字模型的選擇、預失真系統的研究和自適應算法的選擇等.數字預失真模型包括Volterra 模型、MP 模型、廣義MP 模型(general MP,GMP)和Wiener-Hammerstein模型等，目前在工程上應用得最多的模型則是MP，其復基帶模型的表達式如下：

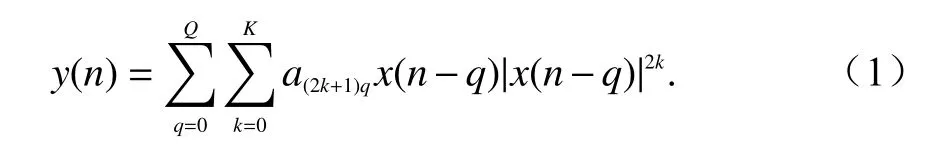
式中：y(n)為 預失真器的輸出信號；Q為記憶深度；K為非線性階數；x(n)為輸入的復基帶信號.MP 模型相較于傳統的Volterra 級數模型與GMP 模型，具有更低的復雜度、較好的擬合精度以及較易的硬件實現難度[8-9]，故本文采用MP 模型進行驗證.

考慮到普通ILA 的數據訓練算法具有較差的帶外抑制效果和不佳的收斂速度，本文根據上述模型和結構，提出了一種基于ILA 的交叉信號訓練預失真系統，系統的原理圖如圖5 所示.

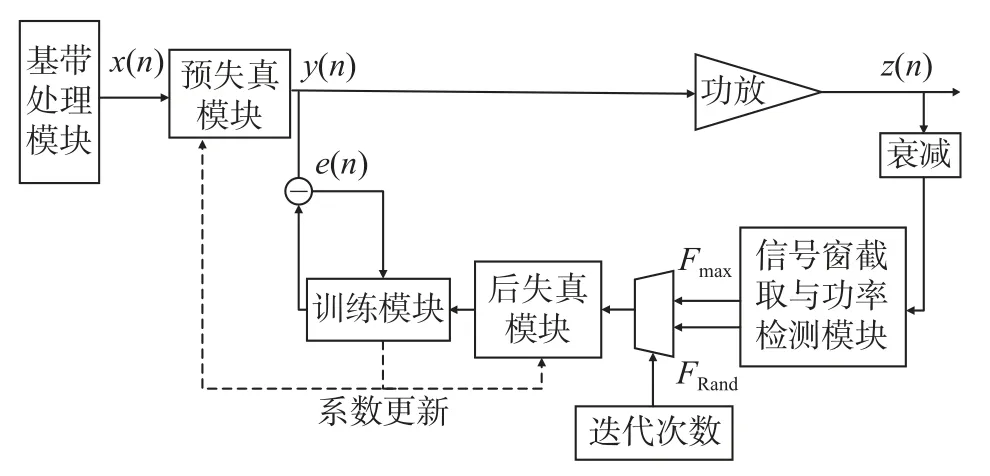
圖5 基于ILA 的交叉信號訓練預失真系統原理圖Fig.5 Cross-signal training pre-distortion structure based on ILA

如圖5 所示，基于該系統的訓練算法將功放的輸出信號反饋至信號截取與功能功率計算模塊，該模塊實質上是一種可滑動的窗函數.截取一定數量的輸入信號并計算其功率，表達式為

通過設置窗函數的長度N，可以計算出流動數據的平均功率.根據功放模型的表達式，功放輸出不僅與當前時刻的輸入有關，也與歷史輸入有關，更與輸入信號的幅度有直接關系，故當功率較大信號在通過功放時，會產生更為嚴重的非線性失真.在圖5 中，大功率數據流為Fmax.

根據圖6 所示，本文針對大功率數據段設計了滑動窗口和功率計算模塊，通過計算信號的平均功率確定大功率數據的區間，然后根據這個區間求取預失真器的參數.窗口長度為N時，平均功率為

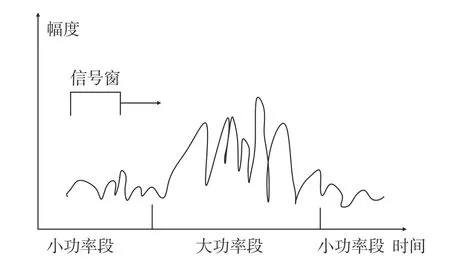
圖6 反饋信號時域參考圖Fig.6 Time domain reference diagram of the feedback signal

大功率信號的定義如下，在反饋信號經過衰減器后，需要篩選出大功率數據段，在本文中，大功率數據段的篩選是根據預失真系統中功放輸出信號的幅度所確定的.非線性系統中，功放的輸入信號中幅度最大的數據段會產生最大的失真，假設輸入的基帶信號數據長度為10 000，設置數據窗長度N為4 096.在第一次迭代計算時，算法會遍歷10 000 個功放輸出數據并截取相應的數據段.比如在處理第一個數據段時，會截取第1～4 096 個功放輸出的所有數據，同時計算出平均功率，以此類推，第2～4 097 個，…，第5 905～10 000 個.在截取完所有功放輸出數據后，比較得出其平均功率最大的數據段，送入自適應算法模塊中進行訓練.

接下來對LS 算法進行分析，LS 算法是對目標函數的一種擬合途徑[9]，根據黑盒系統的輸入輸出信號，估算出黑盒系統的參數與次方項，而預失真系統恰好就是與黑盒系統相類似的非線性系統，可以利用LS 算法估算出預失真器的系統參數[10-11].算法的步驟為：首先設置功放模型為MP 模型，根據模型和輸入y(n)以 及窗函數的長度N建立基底函數Y，公式為

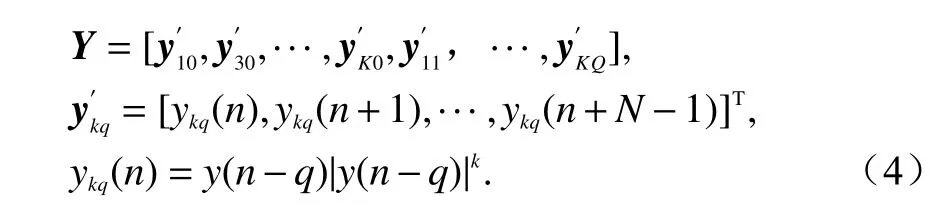
式中：ykq(n)為 MP 的核函數；Y為N×((K+1)×(Q+1))的矩陣，具體表達式為

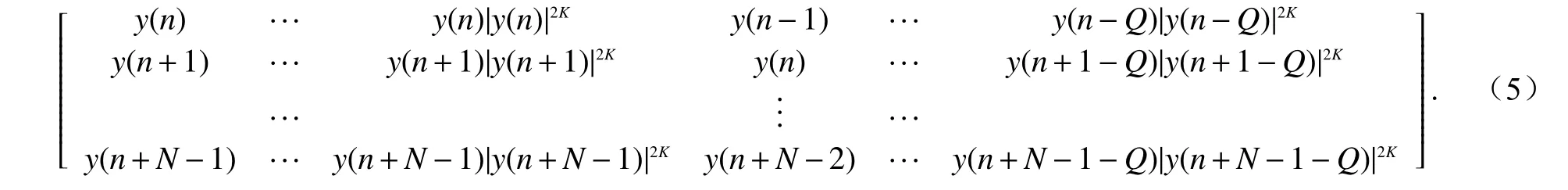
令模型參數A為

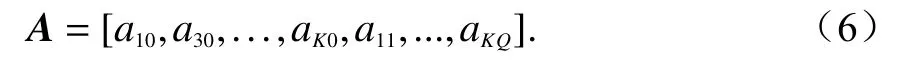
式中a為每個核函數項所對應的參數.輸出信號Z為

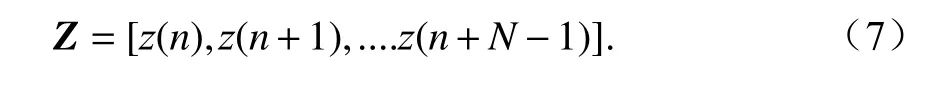
則有等式

故功放的輸入輸出可以看作是一組線性變換，且可以通過LS 算法直接求取功放模型的參數A：

經過滑動窗函數模塊所截取的數據段，在通過后失真模塊后，經過自適應算法模塊，通過式(8)計算出模型系數并復制到預失真模塊中，從而實現功放的線性化.目前，研究人員對ILA 的大功率信號訓練進行了研究[12-14]，根據每次信號窗采集到的信號平均功率，選取出最大功率的信號段送入訓練模塊中，對大功率數據段進行修正，帶外失真取得一定的優化[15-16].但是，僅僅利用大功率數據流來訓練預失真器的參數，并不能達到最好的效果，僅能將失真最大頻段的數據修正回來.故本文引入一種交替擬合的思想，即每經過一次的參數更新，更換一次窗函數截取方法.比如，第一次更新的基底函數為大功率信號，則第二次更新的基底函數為隨機截取的信號，如此反復直至更新至最低的誤差.圖5 中，Frand為隨機窗截取的數據流，同大功率信號段的截取方式相似，隨機信號段的截取方式是在窗函數經過了所有數據段后，隨機抽取一個數據段送入訓練模塊，對失真相對不嚴重的頻段進行一定程度上的修正.本文算法的具體形式如下所示：

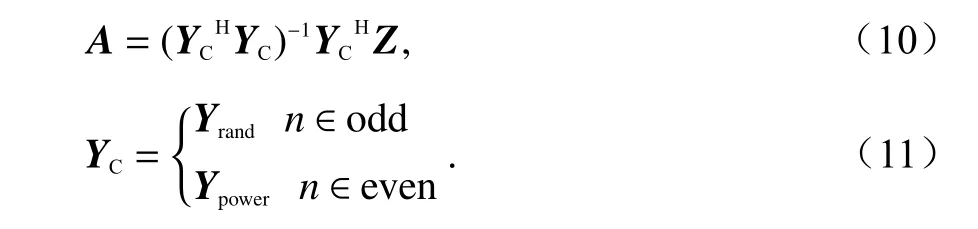
式中：Yrand為反饋信號隨機截取的窗函數的基底函數；Ypower為反饋信號大功率截取的窗函數的基底函數；n為迭代次數.本文擬合的輸出信號Z設置為預失真模塊的輸出信號y(n).在初始狀態時，預失真器的非線性項參數，除了a10之外全設置為0.故在第一次迭代時，基帶輸入信號x(n)和預失真器的輸出y(n)可以看作是等效的，即都是純凈的，未有失真的信號.根據上文的描述，交替迭代的自適應預失真算法流程如圖7 所示.可以看出，本算法在功放輸出的數據段中，分別通過窗函數篩選出功率最大的數據段與隨機數據段，并送入LS 算法模塊中進行訓練，每增加一次迭代次數，轉換一種輸入LS 算法模塊的數據段.

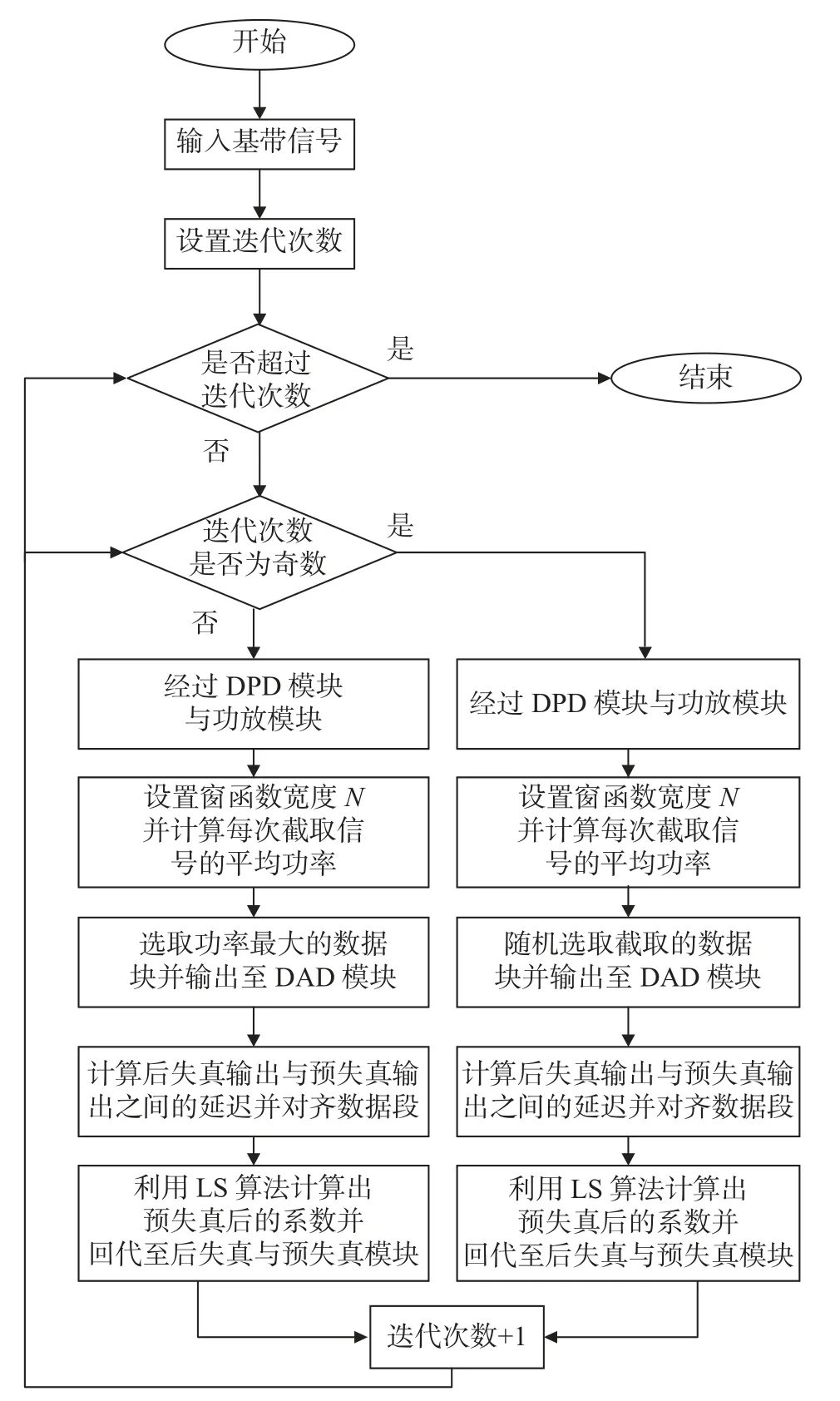
圖7 交替迭代的自適應預失真算法流程圖Fig.7 Flowchart of the alternating iterative adaptive Predistortion algorithm

2 系統仿真

設置輸入信號為LTE 信號，其PAPR 為9 dB，信號功率為0 dBm，信號帶寬為20 MHz，采樣率為245.76 MHz，采樣時間為1 ms，共有245 760 個采樣點.設置信號窗長度N為4 096 個采樣點，本系統的仿真平臺基于射頻在線測試平臺RF WebLab，該平臺的測試結果基于真實的GaN 功放，測試平臺實物如圖8 所示.

圖8 在線測試平臺實物圖Fig.8 Prototype of online test platform

利用MATLAB 搭建好仿真平臺，經過延時對齊、增益對齊等預處理后，接下來分別對順序數據流訓練、大功率數據流訓練和大功率與隨機數據流訓練三種模式的訓練結果進行對比，設置迭代次數為5，分別對原始信號功率譜、經過功放后的功率譜以及預失真系統的輸出頻譜進行仿真.設置MP 模型的記憶深度Q=3，非線性階數K=5.本文將所有功率譜的值均設置為小于0 dB，以便觀察及對比.

圖9(a)～(c)分別為采用順序訓練算法、大功率訓練算法、交叉訓練算法，即采用順序數據流、大功率數據流、大功率與隨機數據流訓練相結合的訓練結果.可以看出：經過5 次迭代后，采用大功率數據流訓練算法的帶外抑制效果在失真頻段相對于順序數據流訓練算法優化了2 dB 左右；而采用大功率訓練與隨機訓練相結合的模式，整體預失真效果改善了3 dB 左右，帶外抑制效果比大功率訓練算法與順序訓練算法都要好.

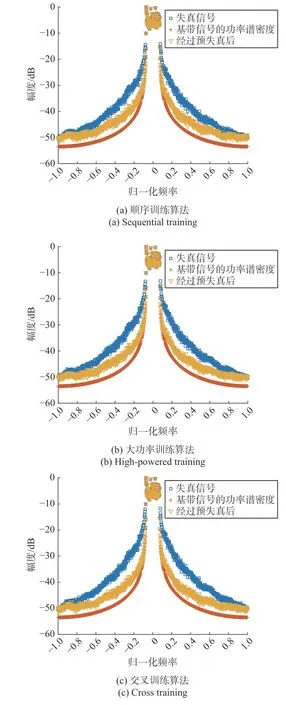
圖9 三種算法的訓練結果Fig.9 Training results of three algorithms

接下來對每次迭代后的NMSE 進行仿真與對比，NMSE 能夠判斷兩組信號的擬合度大小.在本文中用NMSE 衡量已調信號的失真情況，在采用不同預失真算法的情況下，NMSE 的值越小越好[17].

在本文算法中，同樣是利用數據窗對預失真器輸出y(n)與 后失真器輸出z1(n)兩組信號進行截取，設置窗寬度為N.并且對兩組數據進行歸一化處理，保證兩組信號值的變化范圍為[-1,1]，經過歸一化處理后，對NMSE 進行計算，其公式如下：

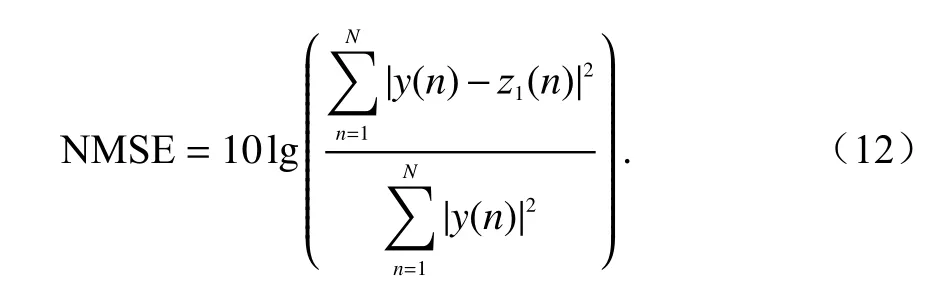
通過比較三種算法在每次迭代后的NMSE 大小，得出每種算法的功放線性化程度，三種算法NMSE 對比如圖10 所示.

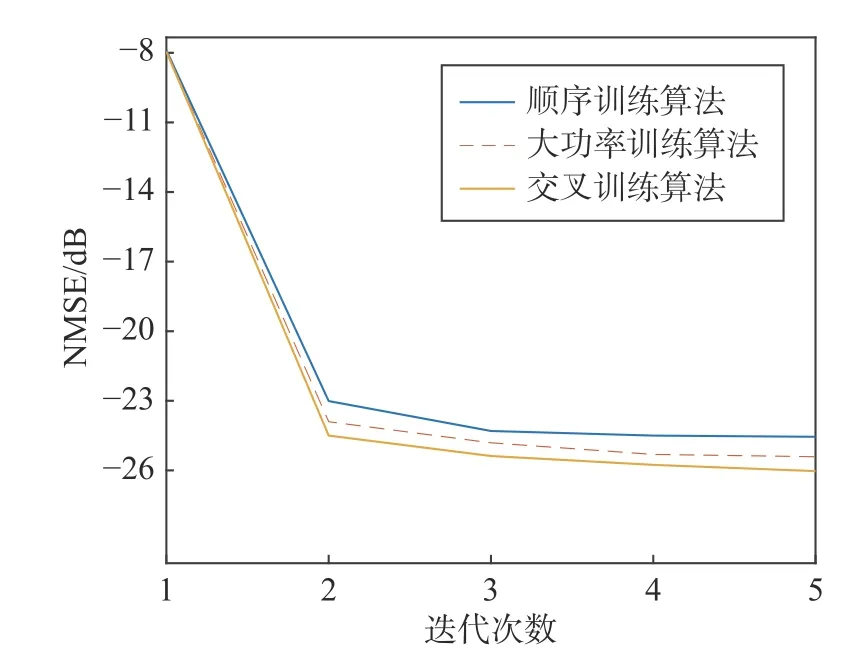
圖10 三種算法的NMSE 對比Fig.10 Comparison of NMSE among three algorithms

由圖10 可以看出：在第一次迭代時，三種算法的NMSE 相差無幾；在第二次迭代時，基于交叉訓練算法的NMSE 分別比順序訓練算法與大功率訓練算法的NMSE 小1 dB 與0.6 dB 左右，且迭代后的NMSE均小于-23 dB.采用本文算法，在接下來的幾次迭代后，系統的NMSE 維持在-25 dB 左右，均比順序訓練法與大功率訓練法低.

表1 為三種算法的性能對比.可以看出，本文所提算法經過5 次迭代后，系統的平均NMSE 分別比順序訓練法與大功率訓練法低了1 dB 與0.5 dB 左右，并且帶外抑制效果也分別比上述兩種算法低了5 dB 與2.5 dB 左右，具有較好的功放線性化效果.

表1 三種算法性能對比Tab.1 Performance comparison of three algorithms

3 結 論

本文所提出的基于ILA 的大功率與隨機信號交替迭代訓練算法比目前常用的順序信號迭代訓練算法和大功率信號迭代訓練算法的帶外抑制效果均有所提升.仿真結果表明，在采用PAPR 為9 dB 的LTE信號進行算法驗證時，新提出的大功率與隨機信號交替迭代算法對功放輸出信號的頻帶外失真頻段的抑制效果，相對于傳統的順序數據流處理算法與大功率數據流處理算法分別優化了5 dB 與2.5 dB 左右，并且在迭代5 次后，采用本算法后的平均NMSE分別比順序信號訓練迭代與大功率信號訓練迭代的NMSE 改善了1 dB 與0.6 dB 左右.