自動實現G1連續的組合曲線曲面構造方法
魏子華,嚴蘭蘭
(東華理工大學理學院,330013,南昌)
0 引言
Bézier方法是現代計算機輔助幾何設計(CAGD)中使用最廣的方法之一,它能夠受到如此廣泛的應用得益于自身的諸多良好性質,例如端點插值、對稱性、幾何不變性與仿射不變性、凸包性等,而它的諸多良好性質都歸功于Bernstein基函數優秀的代數性質。盡管Bézier方法有諸多便捷之處,但它在曲線曲面形狀調整方面仍然存在不足,要想調整曲線曲面的形狀就只有改變控制頂點的位置,這給計算帶來不便的同時還可能會違背設計者的意圖。另外,單一的Bézier曲線曲面要想表示較為復雜形狀就只能提高其次數,但由于Bézier方法具有整體控制卻缺乏局部調整的性質,任何局部的修改都會牽一發而動全身,所以在實際運用中Bézier曲線曲面的次數超過10次是禁忌的[1]。因此為了滿足工業生產對于描述復雜形狀的需求, 往往會采取Bézier曲線曲面組合拼接的方式, 拼接時需要考慮光滑度的問題。對于G1連續,除了需要滿足位置連續以外,還需要滿足3個控制頂點共線, 對此需要通過一定的計算來選取合適的控制頂點。相鄰曲線拼接若要滿足較高光滑度則需要滿足較為復雜的條件。
對于Bézier方法在曲線曲面形狀調整方面的不足,已有許多文獻提出了解決辦法,這類文獻大多是構造含參數的基函數,使其定義的曲線曲面具有類似Bézier曲線曲面的諸多良好性質,且能通過調整形狀參數值來調整曲線曲面的形狀。有的學者在代數多項式空間中對Bézier方法進行改進,例如,王海波等[2]由三次Bernstein基函數擴展定義了一種帶2個形狀參數的四次多項式基函數;Hu Guang等[3]由n次Bernstein基函數定義了帶n個形狀參數的n次多項式基函數(n≥2);李軍成等[4]利用遞推性質定義了帶2個形狀參數的n次曲線(n≥3),對同次Bézier方法進行了擴展;除此之外,文獻[5-7]都是在代數多項式空間上對Bézier方法進行改造。也有學者在非代數多項式空間中對Bézier方法進行改進,例如,張貴倉等[8]在三角函數空間定義了帶4個參數的三次多項式曲線;Hu Guang等[9]在雙曲函數空間定義了帶4個參數的四次多項式曲線曲面;TAN X W等[10]在三角函數空間定義了帶2個參數的五次多項式曲線;除此之外,文獻[11-14]也是在非代數多項式空間進行Bézier方法的擴展。還有學者同時在代數和非代數多項式空間對Bézier方法進行擴展,例如,王成偉[15]以三次Bernstein基函數和二次三角Bézier型曲線的基函數為工具構造了一組帶3個參數的三次基函數;Zhu Yuanpeng[16]等將代數多項式空間的三次Bernstein基函數與指數函數相結合, 構造了一組帶2個參數的三次基函數;拓明秀[17]等將代數多項式空間的三次Bernstein基函數和三角多項式空間的三次類Bernstein基函數相結合構造了一組帶3個形狀參數的三次基函數。從代數多項式空間進行Bézier方法擴展,計算簡單但不能很好地表示圓錐截線,在非代數多項式空間進行Bézier方法擴展,不便于計算但能更好地表示圓錐截線。
文獻[2-17]所定義的曲線曲面,不僅保留了Bézier曲線曲面的諸多良好性質,而且能夠在不改變控制頂點的前提下,通過調整形狀參數來達到改變曲線曲面形狀的目的。但這些文獻鮮有考慮拼接方法的難易性,其中的曲線曲面拼接往往需要較為復雜的條件以實現較高階的幾何連續性或者參數連續,在實現低階連續時也并未給出比Bézier方法更為簡便的拼接條件。
工業生產中對于光滑度要求較低的生活物品的制造,往往不需要高階連續,G1連續足以滿足需求。為了能在簡單條件下實現G1光滑拼接,這里定義了一類n(n≥2)次曲線,它們都可以在不改變控制頂點的情況下,通過改變參數值達到調整首、末端點位置的目的,當n≥4時還可以通過調整參數值自由調整曲線內部形狀。同時定義了對應的曲面,它們和曲線一樣,也可以通過調整形狀參數值達到調整形狀的目的。曲線拼接時,只需第1段曲線控制多邊形的最后一條邊與第2段曲線控制多邊形的第1條邊重合、且兩參數之和為1,即可實現G1連續,同理對應的曲面也可以在簡單的條件下實現G1光滑拼接。
1 基函數的構造及其性質
定義1:對于任意t∈[0,1],參數α,γ∈[0,1)、β∈(0,1],稱如下函數組為帶3個參數的n階Bernstein基函數,簡稱n階αβγ-B基。
當n=2時,稱t的二次多項式
(1)
為2階αβγ-B基;
當n=3時, 稱t的四次多項式
(2)
為3階αβγ-B基;值得注意的是,當n=3時t的三次多項式同樣存在,t的三次多項式為
由于n=3時的四次多項式更符合不同階αβγ-B基的構造方式,且能更精確地表示圖形,同時為在后文的證明及拼接不引發歧義,故n=3時都采用t的四次多項式。當n為偶數且n≥4時,稱t的n+1次多項式
(3)
為n階αβγ-B基;當n為奇數且n≥5時稱t的n+1次多項式
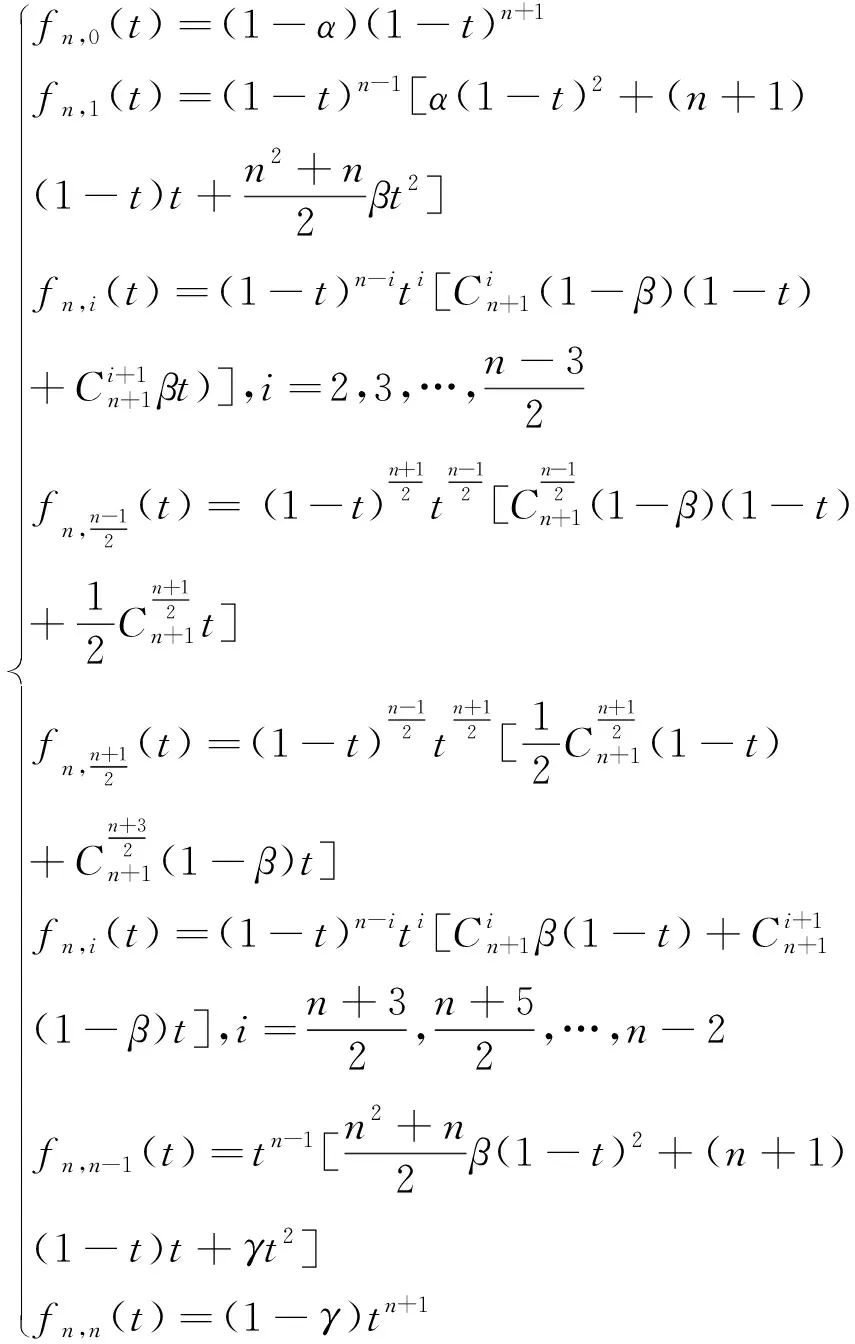
(4)
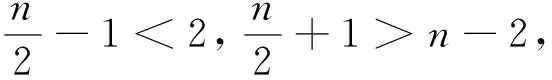
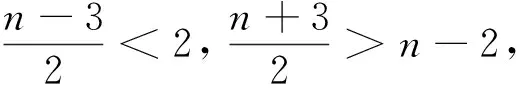
下面用Bernstein基函數來表示n階αβγ-B基,其中當n=2時
(5)
當n=3時
(6)
當n為偶數且n≥4時
(7)
當n為奇數且n≥5時
(8)
由定義容易得到αβγ-B基的如下性質。
1)非負性:當參數α,γ∈[0,1),β∈(0,1]時,對任意t∈[0,1]都有fn,i(t)≥0(n=2,3,4,…, 0≤i≤n)。
證明:由Bernstein基函數的非負性以及參數范圍容易得到式(5)~式(8)中fn,i(t)≥0(n=3,4,…,0≤i≤n)。
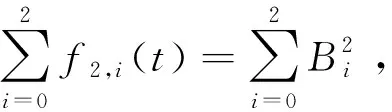
3)對稱性:對任意t∈[0,1],當α=γ時,有fn,i(t)=fn,n-i(1-t)。
證明:由式(5)~式(8)及Bernstein基函數的對稱性易知。
4)端點性質:對n=2,3,4,…,0≤i≤n,αβγ-B基在端點處的函數值如下
(9)
當n=2時αβγ-B基在端點處的一階導如下:
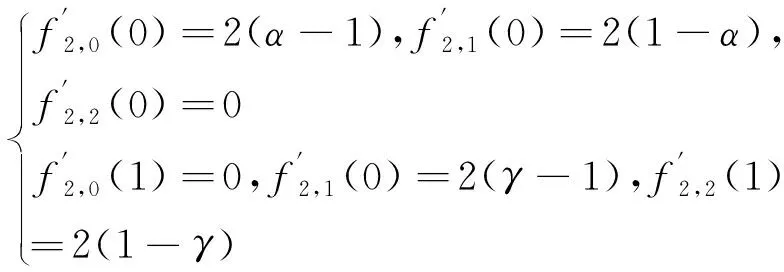
(10)
當n=3,4,…, 0≤i≤n時αβγ-B基在端點處的一階導如下:
(11)
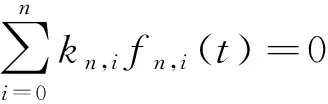
證明:假設
(12)
其中kn,i∈R。
①當n=2時,將式(5)代入式(12)中,整理得
由二次Bernstein基函數的線性無關性可知
k2,0(1-α)+k2,1α=0;k2,1=0;k2,1γ+k2,2(1-γ)=0
易得此方程組的解為k2,i=0(i=0,1,2)。
②當n=3時,將式(6)代入式(12)中,整理得
由四次Bernstein基函數的線性無關性可知
易求得此方程組的解為k3,i=0(i=0,1,2,3)。n≥4時同理可證。
2 曲線及其應用
2.1 曲線的定義及性質
定義2:給定n+1個控制頂點Pi∈d(d=2,3, 0≤i≤n,n≥2),參數α,γ∈[0,1),β∈(0,1], 對任意t∈[0,1],定義曲線
為n階αβγ-Bézier曲線。
αβγ-Bézier曲線具有如下性質。
1)端點性質:由αβγ-B基的端點性質,可以推出對于n=2,3,4,…,0≤i≤n,αβγ-Bézier曲線的端點位置如下
(13)
當n=2時,αβγ-Bézier曲線的端點導矢如下
(14)
當n=3,4,…, 0≤i≤n時,αβγ-Bézier曲線的端點導矢如下
(15)
2)幾何不變性:由αβγ-B基的規范性可知,αβγ-Bézier曲線的形狀不依賴坐標系的選取。
3)凸包性:由αβγ-B基的規范性和非負性可知,αβγ-Bézier曲線rn(t)恒位于由控制頂點Pi(0≤i≤n,n≥2)確定的凸包中。
4)形狀可調性:在不改變控制頂點位置的條件下,調整αβγ-B基中的任意參數值,都能改變αβγ-Bézier曲線的形狀,其中調整參數α會影響曲線的起點位置,調整參數β不會影響曲線起點和終點的位置但會改變曲線內部形狀,改變γ會影響曲線的終點位置(見圖1~圖3)。
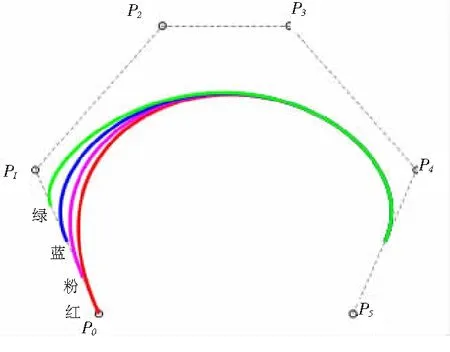
圖1 僅改變參數α
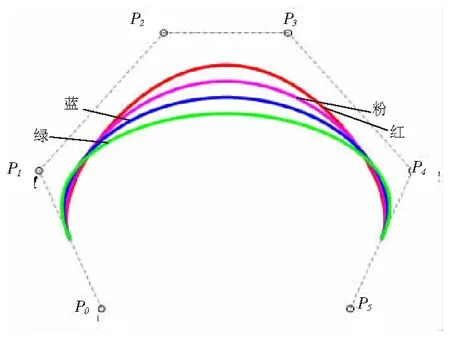
圖2 僅改變參數β
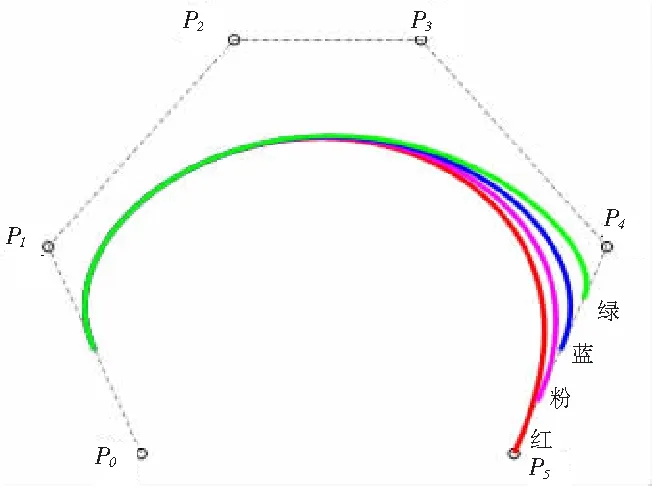
圖3 僅改變參數γ
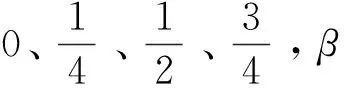
從圖1可以看出僅改變參數α時曲線的起點位置會發生改變,α越小起點越靠近首個控制頂點,當α=0時曲線首端與首個控制頂點重合;從圖2可以看出僅改變參數β時曲線的起點和終點位置不發生改變,但曲線形狀會改變;從圖3可以看出僅改變參數γ時曲線的終點位置會發生改變,γ越小終點越靠近最后一個控制頂點,當γ=0時曲線末端與最后一個控制頂點重合。
5)對稱性:由αβγ-B基的對稱性知,當α=γ時,控制頂點Pi(i=n,n-1,…,0;n≥2)和Pi(i=0,1,…,n;n≥2)定義的αβγ-Bézier曲線具有相同的形狀。由圖1~圖3易知。
2.2 曲線的G1拼接條件
由于G1連續條件對于曲線而言要求不高,在低階曲線上的適用性更強,故先討論所構造的低階曲線拼接條件。
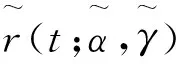
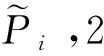
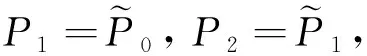
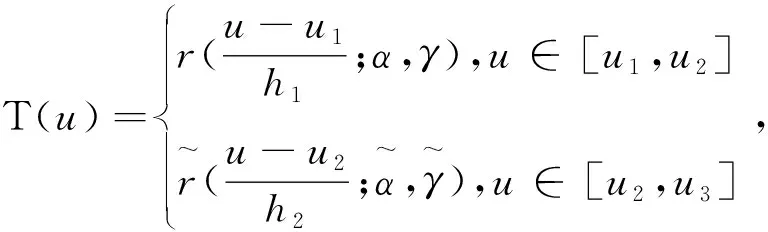
(16)
其中,h1=u2-u1,h2=u3-u2。
由式(13)、式(16)可知
(17)
由式(14)、式(15)及式(16)可知
(18)
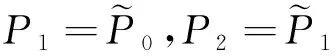
即滿足G1連續條件,故曲線T(u)在公共連接點處G1連續。雖然低次曲線G1連續拼接更有意義,但任意次曲線的G1連續拼接能為工業生產制造提供更多選擇,故下面討論任意次曲線的G1拼接條件。
設有m條大于等于二階的αβγ-Bézier曲線段
其中j表示曲線段的序號,第j條曲線的階用nj表示,Pj,i表示第j條曲線的第i+1個控制頂點,αj,βj,γj表示第j條曲線段的參數,其中二階和三階αβγ-Bézier曲線段中不含參數β,在運用時注意省略。j=1,2,…,m,0≤i≤nj,m≥2,nj≥2,t∈[0,1],αj,γj∈[0,1),βj∈(0,1]。
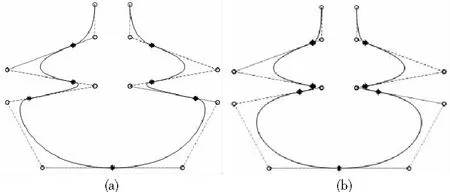
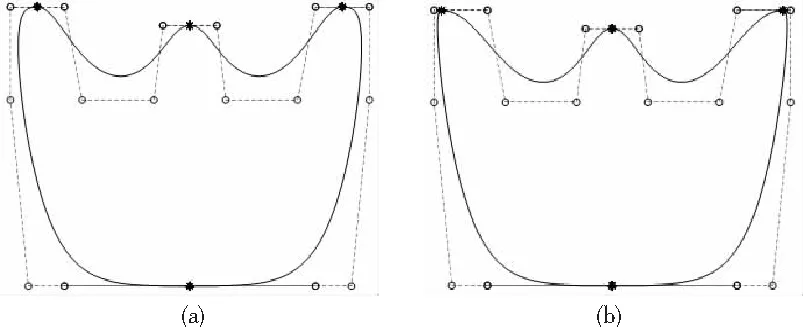
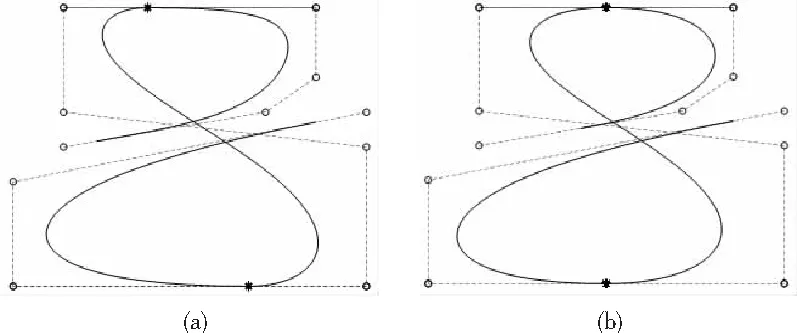
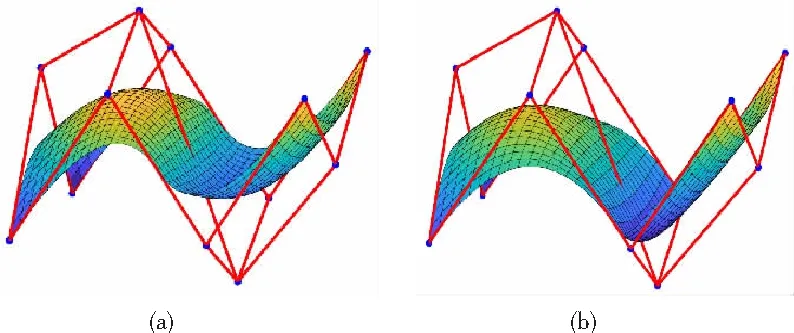
定理1:給定節點向量u1 (19) 其中hj=uj+1-uj,j=1,2,…,m。 若這m條曲線段的控制頂點和形狀參數滿足條件 (20) 則曲線R(u)在公共連接點處G1連續。 證明:由式(13)及式(19)可知 (21) 當nj-1=nj=2時,由式(14)及式(19)可知 (22) 當nj-1=2,nj≥3時,由式(14)、(15)及式(19)可知 (23) 當nj-1≥3,nj=2時, 式(14)、(15)及式(19)可知 (24) 當nj,nj-1≥3時,由式(15)及式(19)可知 (25) 要使曲線R(u)在公共連接點處G1連續,需滿足 (26) 給定m條大于等于二階的αβγ-Bézier曲線段,假設所要構造的組合曲線是由這m條曲線段組成的。由2.2節中約定的記號可知,組合曲線的首、末兩端控制頂點分別為P1,0和Pm,nm,每段曲線的內控制頂點為Pj,i(j=1,2,…,m, 0≤i≤nj),由定理1可知只要控制頂點滿足Pj-1,nj-1-1=Pj,0,Pj-1,nj-1=Pj,1,參數滿足αj=1-γj-1,組合曲線在公共連接點處就滿足G1連續,其中j=2,3,…,m。 注:要想構造封閉的組合曲線,除了滿足上述要求,還需滿足Pm,nm-1=P1,0,Pm,nm=P1,1,α1=1-γm,以此保證組合曲線首尾相接且在連接處G1連續。 圖4~圖6為用上述方法構造的組合曲線,其中空心圓點代表控制頂點,星號表示分段連接點。 圖4 插值于首、末端點的G1連續開曲線 圖5 G1連續閉曲線 圖6 未插值于首、末端點G1連續開曲線 由圖4~圖6可見不同次數的αβγ-Bézier曲線可以自由拼接,拼接時能夠在不改變控制頂點的前提下,通過改變其中的形狀參數局部調整曲線形狀。從圖4和圖6中可以看出組合αβγ-Bézier曲線可以插值于首、末端點,也可以不插值于首、末端點,這取決于第一段的參數α和最后一段的參數γ取何值。 眾所周知G1拼接涉及到第1段曲線的后2個控制頂點和第2段曲線的前2個控制頂點,G2拼接涉及到第1段曲線的后3個控制頂點和第2段曲線的前3個控制頂點。對于高階曲線而言G2連續是比G1連續更好的連續性選擇,但所需滿足的條件也隨之提高。下面將討論2條三階αβγ-Bézier曲線的G2連續拼接條件。 設有2條三階αβγ-Bézier曲線段 給定節點u1 (27) 其中,h1=u2-u1,h2=u3-u2。 給定定理1中的條件,由式(13)、式(27)可知 (28) 由式(15)、式(27)可知 (29) 由式(2)可知三階αβγ-B基在端點處的二階導如下 可推知三階αβγ-Bézier曲線在端點處的二階導如下 (30) 要使得組合曲線在拼接點處G2連續,則需要滿足 (31) 由組合曲線滿足定理1中給定的預處理條件可知T(u)在拼接點處G1連續,即滿足式(31)中的條件(a)、(b),只需要再滿足式(31)中的條件(c),組合曲線T(u)在拼接點處就能夠達到G2連續。 (32) 即對于任意的參數λ2而言,只要控制頂點滿足式(32),組合曲線就能達到G2連續。 定義3:給定(m+1)×(n+1)個控制頂點Pij∈3(i=0,1,…,m,i=0,1,…,n,m,n≥2),參數α1,γ1,α2,γ2∈[0,1),β1,β2∈(0,1],對任意u,v∈[0,1],定義曲線 為m×n階αβγ-Bézier曲面。 αβγ-Bézier曲面具有與αβγ-Bézier曲線類似的性質,例如幾何不變性、對稱性、形狀可調性、凸包性等。下面給出αβγ-Bézier曲面的拼接條件及證明。 定理2:設有若干個m×nk階的αβγ-Bézier曲面 (33) (34) 則曲面p(u,v)在公共連接線處G1連續。 證明:由式(9)、式 (33)可得 (35) 由式(10)、式(35)可知,當nk=2時,有 (36) 當nk-1=2時,有 (37) 由式(11)、式(33)可知,當nk≥3時,有 (38) 當nk-1≥3時,有 (39) 若階為m×nk-1的曲面與階為m×nk的曲面滿足 (40) 則組合曲面在拼接處G1連續。 圖7 G1連續組合曲面 本文定義了n階αβγ-Bézier曲線,并將其推廣至曲面,定義了m×n階αβγ-Bézier曲面。該曲線具有Bézier曲線的諸多良好性質,且能夠在不改變控制頂點的情況下通過調整參數改變形狀。二階和三階αβγ-Bézier曲線在端點處可調,更高階的曲線在端點處及內部都可調,同時αβγ-Bézier曲線的G1拼接條件非常簡便。但是由于提高二階Bézier曲線的次數會使得參數的選取范圍受限,影響其他次數的曲線構造,因此構造二階αβγ-Bézier曲線曲面時相對于二階Bézier而言并未提高次數。G1連續是工業設計中較為實用的一種連續條件,能滿足大多數簡單工藝生產的需求。本文給出的曲線曲面既能比Bézier曲線更易于實現G1連續拼接,而且能實現在不改變控制頂點的前提下自由調整形狀的目標,因此使用更加方便。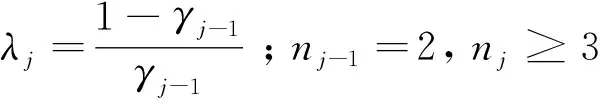
2.3 G1連續組合曲線的構造
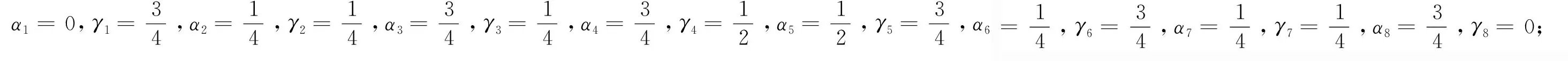
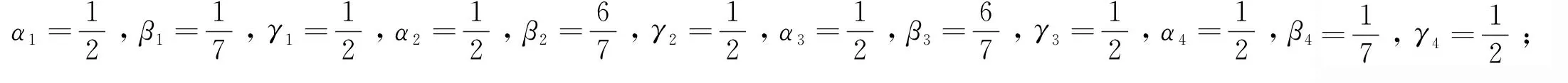
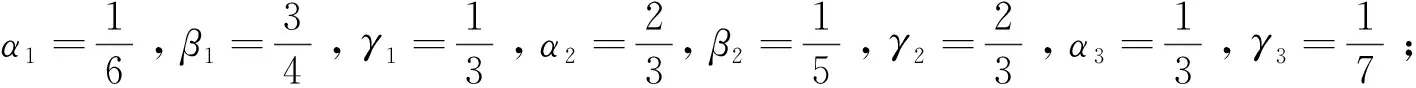
2.4 曲線的G2拼接條件
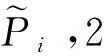
3 曲面及其應用
3.1 曲面定義及G1連續拼接條件
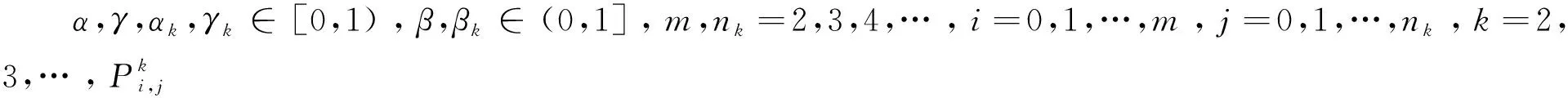
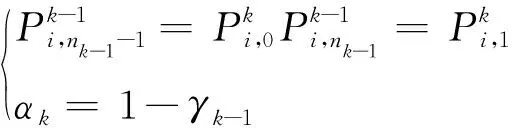
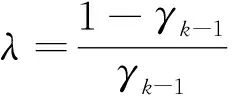
3.2 G1連續組合曲面的構造
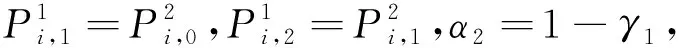
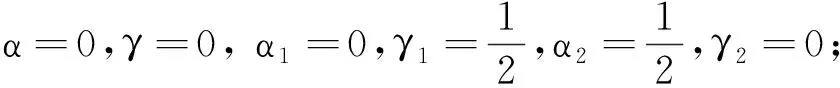
4 結束語

