基于雙折線抗力模型的空爆荷載梁式構件振動位移研究*

耿少波，陳佳龍，趙 洲，牛艷偉

（1. 中北大學理學院土木工程學科部，山西 太原 030051；2. 長安大學公路大型結構安全教育部工程研究中心，陜西 西安 710064）

等效單自由度（single degree of freedom，SDOF）方法作為一種計算效率高的動力分析方法，廣泛用于工程抗爆規(guī)范[1-4]，也常作為校核手段用于梁式構件空爆荷載試驗的位移分析[5-10]。考慮到建筑結構空爆荷載是一種概率較低的偶然作用，進行SDOF 梁式構件位移分析時，建筑抗爆規(guī)范和大多數(shù)試驗設計允許梁式構件具有一定程度的塑性位移。這也表明SDOF 體系的構件剛度應包含彈性和塑性兩部分；在表征塑性剛度時，常采用忽略塑性抗力的理想彈塑性抗力模型[1-6,8,10]。因此，開展空爆荷載梁式構件振動位移精細化理論研究，有助于對彈塑性位移振動全過程的理解，也有利于對延性比、荷載時長等參數(shù)的準確把握。

從爆炸試驗來看，陳萬祥等[10]、Li 等[11]、Stochino 等[12]和Zhang 等[13]的鋼筋混凝土梁爆炸試驗，Rokaya 等[14]的鋼梁爆炸試驗，Bruhl 等[15]的高強低合金鋼梁爆炸試驗，在塑性階段均呈現(xiàn)了抗力強化且抗力剛度小于彈性階段的特征。Fallah 等[16]也認識到塑性抗力較彈性抗力增大的特性，開展了爆炸作用梁式構件無阻尼、塑性強化抗力的超壓-沖量曲線研究。方秦等[17-18]采用理想彈塑性抗力模型，研究了阻尼參數(shù)對爆炸作用梁動力響應的影響；耿少波等[19-20]開展了理想彈塑性抗力模式下阻尼參數(shù)在指數(shù)型爆炸荷載下對梁式構件振動動力系數(shù)的影響；郭東等[21]指出在空爆這種極短的荷載作用下，阻尼對構件進入塑性階段后的反彈位移存在影響。目前，開展的空爆作用梁式構件的響應及位移分析所采用的理想彈塑性抗力模型較簡單，未對爆炸作用下梁式構件塑性階段抗力強化效應的位移影響作深入研究，也未對爆炸作用下柔性構件和剛性構件進行區(qū)分對待。

雙折線抗力模型是一種良好的、可精準描述塑性階段抗力強化的本構關系[22-23]，且它可退化為理想彈塑性抗力模型。若將該模型運用于空爆作用梁式構件振動位移分析，會得到更精準的彈塑性位移分析結果，也可以比較出常規(guī)彈塑性抗力模型對應的計算精度。本文中，對空爆作用梁式受力構件柔性、剛性分類后，分別采用雙折線抗力模型建立精細化SDOF 振動方程，由阻尼比與塑性抗力強化系數(shù)關系求解各條件下構件振動位移的解析解；結合典型工況，分析雙折線抗力模型中塑性強化參數(shù)對最大彈塑性位移、塑性回彈位移和殘余變形等的影響，以期為工程抗爆提供精細化理論依據(jù)。

1 空爆荷載柔性構件正向振動動力響應求解

1.1 空爆荷載柔性構件的定義

定義ti為空爆荷載作用時長，te為構件空爆作用下從靜止至完成正向振動彈性狀態(tài)所需時長。當ti＜te時，爆炸荷載作用結束時構件尚未完成彈性振動，稱此類構件為柔性構件。由于常規(guī)武器空爆荷載作用時間ti很短，往往小于構件達到最大彈塑性變形的所需時長tm[1]，即柔性構件時長參數(shù)的關系為ti＜te＜tm。

1.2 彈性階段強迫振動

空爆作用梁式構件等效SDOF 法最早被Biggs 使用[23]，如圖1(a)～(b)所示。采用雙折線抗力模型正向和回彈振動的構件抗力與變形的關系如圖1(c)所示，具體表達式為：

式中：rm為構件彈性階段最大抗力，Rm為構件彈塑性階段最大抗力，Ke為構件彈性階段等效剛度，Kp為構件塑性階段等效剛度。因此，彈性階段等效SDOF 振動方程為：

式中：Me為等效質量，Ce為等效阻尼，y為構件的振動位移，Δpe(t)為等效構件所承受的等效空爆荷載。各等效參數(shù)計算公式分別為：

式中：m為構件線密度，l為構件跨長，ξ 為構件阻尼比，K為構件剛度，kM為彈性階段質量變換系數(shù)，kL為彈性階段荷載變換系數(shù)。

由 GB 50038—2005《人民防空地下室設計規(guī)范》[1]，空爆荷載為：

式中：Δpm為構件超壓線荷載峰值。

求解方程(2)，可得構件位移、速度表達式分別為：

式中：ω 為構件無阻尼振動頻率，ωd為構件阻尼振動頻率，yst為空爆峰值作為靜載時構件靜位移。ω、ωd和yst的計算公式分別為：

將ti代入式(5)～(6)，得到構件強迫振動結束時位移yi和速度vi分別為：

1.3 彈性階段自由振動

空爆荷載作用消失后，構件進入以位移yi、速度vi為初始條件的彈性自由振動，即ti＜t＜te時，構件等效SDOF 方程為：

求解方程(10)，得到位移和速度分別為：

其中：

構件在te時刻達到彈性振動最大位移，此時位移和速度的表達式分別為：

1.4 塑性階段自由振動

彈性振動結束后，構件進入以ye和ve為初始條件的塑性自由振動，即te＜t＜tm時，考慮雙折線抗力模型中構件的塑性階段抗力強化的等效SDOF 方程為：

式中：me為等效質量，ce為等效阻尼力。Me、ce、Ke和Kp的計算公式分別為：

式中：α 為構件塑性階段與彈性階段等效剛度之比，被稱為塑性強化系數(shù)；km和kl分別為塑性階段質量和荷載變換系數(shù)。根據(jù)阻尼比ξ 和塑性強化系數(shù)α 大小關系，方程(16)需按3 種情況分別求解。

(1)當ξ2＜α 時，方程(16)的位移和速度解分別為：

將初始條件ye和ve代入式(18)～(19)，解得C1和C2分別為：

(2)當ξ2=α 時，方程(16)的位移和速度解分別為：

且可解得C3和C4分別為：

同理，可求得：

(3)當ξ2＞α 時，方程(16)的位移和速度解分別為：

且可解得C5和C6分別為：

同理，可求得：

2 空爆荷載剛性構件動力響應求解

2.1 空爆荷載剛性構件定義

與柔性構件定義類似，空爆作用時長內構件從靜止進入彈性繼而塑性振動，空爆作用結束后構件繼續(xù)塑性振動至最大彈塑性位移，稱此類構件為剛性構件，其時長參數(shù)大小關系為：te＜ti＜tm。

2.2 彈性階段強迫振動

剛性構件在此彈性階段，即0＜t＜te時，其等效SDOF 方程與式(1)相同，由式(4)～(5)，得到剛性構件彈性振動結束時的位移和速度分別為：

2.3 塑性階段強迫振動

剛性構件剛進入塑性振動時，空爆荷載尚未消失，即當te＜t＜ti時，其等效SDOF 方程為：

類似于柔性構件塑性階段自由振動求法，對方程(32)也分3 種情況進行求解。

(1)當ξ2＜α 時，方程(32)的位移和速度解分別為：

將初始條件ye、ve代入式(33)～(34)，解得C7和C8分別為：

(2)當ξ2=α 時，方程(32)的位移和速度解分別為：

且可解得C9和C10分別為：

(3)當ξ2＞α 時，方程(32)的位移和速度解分別為：

且可解得C11、C12分別為：

依ξ2與α 的大小關系，將t=ti分別代入上述位移和速度表達式，即可得空爆荷載結束時對應各情況的yi和vi。

2.4 塑性階段自由振動

空爆荷載作用結束后，柔性構件進入以yi、vi為初始條件的塑性階段自由振動，即ti＜t＜tm時，考慮塑性階段強化效應的等效SDOF 方程為：

類似于柔性構件塑性階段自由振動求法，方程(42)也需分3 種情況進行求解。

(1)當ξ2＜α 時，方程(42)的位移和速度解分別為：

將初始條件yi、vi代入式(43)～(44)，解得C13和C14分別為：

令式(44)中v=0，可得構件達到正向振動最大位移ym對應的總時長為：

(2)當ξ2=α 時，方程(42)的位移和速度解分別為：

且可解得C15和C16分別為：

即：

(3)當ξ2＞α 時，方程(42)的位移和速度解分別為：

且可解得C17、C18分別為：

即：

依ξ2與α 的大小關系，將t=tm分別代入上述位移和速度表達式，即可得正向彈塑性振動結束時對應的各ym、vm值。

3 兩類構件回彈階段動力響應求解

3.1 彈性回彈階段

構件正向振動至tm時刻達到彈塑性位移峰值ym時，振動速度vm為零，構件抗力也達到彈塑性抗力最大值Rm，開始反方向的彈性回彈振動。結合式(1)和圖1(c)，此時構件等效SDOF 方程為：

解方程，得到該階段的位移和速度分別為：

將ym和vm代入式(56)～(57)，解得C19和C20分別為：

若構件振動無塑性回彈，令式(57)中v=0，可得構件達到回彈位移最大值對應的時間。若構件振動有塑性回彈，令式(56)中y=ym-2ye對應的時間即為彈性回彈總時長tn，將tn代入式(56)～(57)可得到構件第一次回彈最大彈性位移yn和速度vn。

3.2 塑性回彈階段

若構件彈性回彈位移量自0 開始至ym-2ye范圍內，其振動速度均不為0，構件將會進入塑性回彈狀態(tài)，此時構件等效SDOF 方程為：

方程(59)仍需分3 種情況進行求解。

(1)當ξ2＜α 時，方程(59)的位移和速度解分別為：

將初始條件yn和vn代入式(60)～(61)，解出C21和C22分別為：

(2)當ξ2=α 時，方程(59)的位移和速度解分別為：

且C23和C24分別為：

(3)當ξ2＞α 時，方程(59)的位移和速度解分別為：

且C25和C26分別為：

若令各情況下速度為0 對應的t為，此對應的位移為構件回彈階段最大彈塑性位移。

3.3 第二次彈性回彈

求解后得到此階段的位移和速度解分別為：

4 典型工況計算分析

4.1 典型工況及計算結果

為考查雙折線抗力模型塑性強化系數(shù)對空爆作用兩類構件動位移響應的影響，以簡支梁為受力構件，在彈塑性等效質量-荷載系數(shù)之比kM-L/km-l按文獻[23] 取1.18，典型阻尼比ξ=0.1，荷載時長參數(shù)ωt=0～50 下，抗力強化系數(shù)α=0～0.2 范圍內開展研究，采用塑性強化系數(shù)分別為0、0.01、0.05、0.10、0.20 等5 種典型工況數(shù)值，分別表征無、低、中低、中高、高等5 種類型強化程度。

取ωti=0.2, ωti=2.0 分別為柔性構件、剛性構件典型參數(shù)，其空爆作用下彈塑性振動時程曲線分別如圖2～3 所示。

4.2 結果分析

以理想彈塑性即α=0 工況計算的延性比β、殘余變形yr數(shù)值為基準，雙折線抗力模型中塑性強化系數(shù)α＞0 典型工況的延性比β 和殘余變形yr的計算差異性分別記作γβ和γr，其數(shù)值如表1 所示。

由圖2、表1 可知：柔性構件（ωti=0.2）無量綱處理后的各工況最大彈性位移ye/yst均為0.049 1、延性比β=2 時，α=0.01～0.20 對應的各工況延性比降低范圍在0.5%～3.5%；若柔性構件（ωti=0.2）各工況最大彈性位移ye/yst為0.026 9、延性比β=5 時，α=0.01～0.20 對應的各工況延性比降低范圍在1.2%～15.6%。值得注意的是：柔性構件β=2 時，只有α=0.20 工況存在塑性回彈振動，其殘余變形是理想彈塑性抗力體系計算結果的70.1%，降低程度達30.1%；柔性構件β=5 時，α=0.05, 0.10, 0.20 等3 種工況均存在塑性回彈振動，其殘余變形降低程度隨α 的增大而提高，最大降低程度約為60.7%。

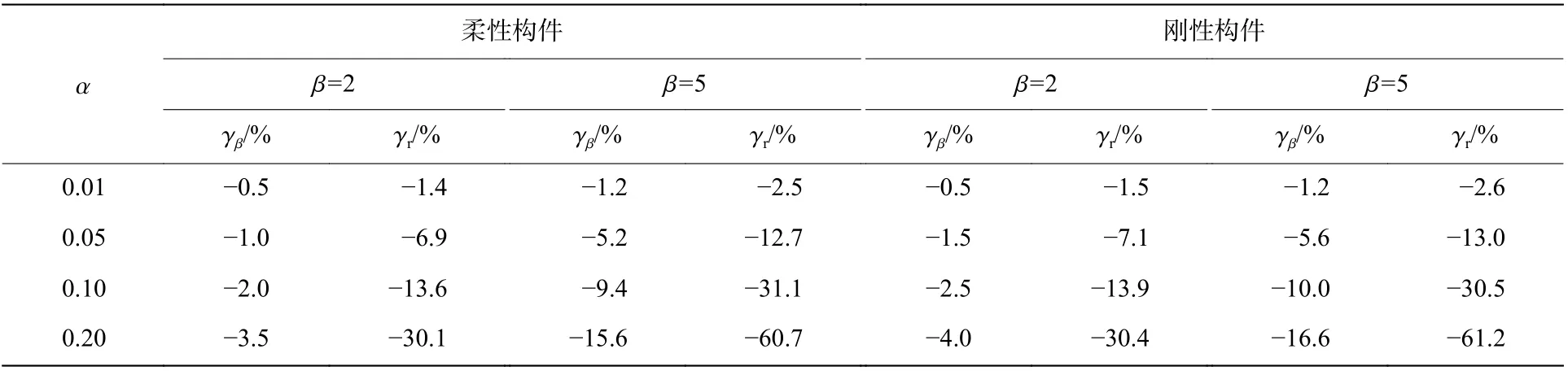
表1 相對于理想彈塑性抗力模型的差異性結果Table 1 Difference results relative to ideal elastoplastic resistance model

由圖3、表1 可知：剛性構件（ωti=2.0）無量綱處理后的各工況最大彈性位移ye/yst均為0.573 7 或0.356 5，且延性比仍為β=2 或5 時，α=0.01～0.20 對應的各工況延性比降低范圍在0.5%～4.0%及1.2%～16.6%，與柔性構件規(guī)律差異性很小，β=2 時仍是只有α=0.20 工況存在塑性回彈振動，β=5 時，α=0.05, 0.10,0.20 等3 種工況均存在塑性回彈振動，其殘余變形隨α 的增大而降低的程度與柔性構件仍較類似。

可以看出，塑性強化系數(shù)α 對兩類構件的影響規(guī)律及程度基本一致。延性比較小（如β=2）時，強化系數(shù)α 對所有工況的最大彈塑性位移ym影響均在4.0%以內，影響非常小，在構件進行抗爆設計時，均可忽略塑性強化抗力的影響。延性比較大（如β=5）時，強化系數(shù)α≤0.05 對最大彈塑性位移ym影響在5.7%以內，α=0.20 對最大彈塑性位移ym影響在16.0%左右。強化系數(shù)α 對存在塑性回彈的工況殘余變形影響顯著，若忽略塑性強化抗力，采用理想彈塑性抗力模式完成構件位移分析，將對殘余變形計算結果產生很大誤差。

由上述分析可知：延性比較大時，即彈塑性位移中塑性位移成分較大時，兩類構件在較小的塑性強化系數(shù)下，仍能進入塑性回彈。從理論上看：當ym-2ye＞時，可進入塑性回彈；ym-2ye＜時，無法進入塑性回彈。考慮到阻尼比ξ 對構件塑性回彈存在影響，補充ξ=0.05 工況，并對ym-2ye與做差后除以yst，完成無量綱處理，作為坐標縱軸參數(shù)，以塑性強化系數(shù)α 為坐標橫軸參數(shù)，其匯總結果見圖4。

由圖4 可知：在相同的延性比β、阻尼比ξ 下，兩類構件在進入塑性回彈時對應的塑性強化系數(shù)α 數(shù)值并無差別；延性比越大、阻尼比越小，構件越易進入塑性回彈，如β=5, ξ=0.05 時，構件進入塑性回彈對應的塑性強化系數(shù)最小值為0.019，而β=2, ξ=0.1 時對應的塑性強化系數(shù)最小值增大為0.155。

5 結 論

(1)提出了基于雙折線抗力模型的兩類梁式構件空爆荷載下振動位移分析方法，給出了梁式構件彈塑性正向振動和彈塑性回彈振動的位移解析解，該方法比理想彈塑性抗力模型方法適用范圍更廣，更具有普遍意義。

(2)相同條件下，隨著雙折線抗力模型塑性強化系數(shù)的增大，兩類梁式構件的最大彈塑性位移、殘余變形均會減小，且殘余變形比最大彈塑性位移降低程度更明顯，當塑性強化系數(shù)較大時，會出現(xiàn)塑性回彈現(xiàn)象。

(3)延性比為2.0 時，塑性抗力強化系數(shù)對兩類構件的最大彈塑性位移影響均較小，其最大彈塑性位移計算誤差在4%以內，進行構件抗爆設計時可忽略塑性強化抗力因素；但在進行殘余變形計算分析時，忽略塑性強化系數(shù)將會過高估計殘余變形數(shù)值，帶來較大誤差。

(4)在相同的延性比、阻尼比下，兩類梁式構件在進入塑性回彈時對應的塑性強化系數(shù)數(shù)值并無差別，且延性比越大、阻尼比越小，構件越易進入塑性回彈。