大容量儲能鋰電池電芯產熱特性研究

孔文俊，張艷森，湯效平，張偉闊*

（1.北京航空航天大學宇航學院，北京市 昌平區 102206；2.華電電力科學研究院有限公司，浙江省 杭州市 310030）

0 引言

近年來，在能源短缺和環境污染的雙重壓力下，尤其是“雙碳”目標驅動下，新能源和可再生能源得到了大力發展，使得電力的生產、傳輸和消費方式發生了根本性的變革，新能源發電將由以往的輔助能源、補充能源逐步發展成為主導能源、替代能源。新能源出力具有隨機性、波動性特點，隨著大規模新能源電力接入電網，電力系統需要在隨機波動的負荷需求與電源之間實現能源供需平衡，其結構形態、運行控制方式以及規劃建設與管理方式將發生重大變革，形成以新能源電力生產、傳輸和消費為主體的新型綜合能源系統，要求源、網、荷、儲等多要素、多主體協調互動，以提高綜合能源系統的安全性、靈活性和綜合利用效率。儲能是新能源大規模利用的重要組成部分，大規模新能源并網的長時間尺度儲能技術是新型綜合能源系統為應對新能源發電不確定性、保障電力連續可靠供應亟待突破的關鍵技術之一。鋰離子電池儲能技術具有效率高、能量密度大、響應速度快、使用壽命長等優點，因而成為當前儲能的主流技術之一，在電網深度調峰和新能源消納領域有重要的應用前景[1-2]。鋰離子電池單體電芯的最佳工作溫度范圍通常在10～35℃，其工作溫度區間在-20～45℃，可承受溫度區間在-40～60℃。鋰離子電池工作時會產生大量熱量，過高的溫度和電池芯之間不均勻的溫差將導致電池芯性能退化，并威脅儲能系統的安全。因此，需要通過電熱管理設計以及溫控技術來維持儲能系統合理的運行環境，以保持均勻的溫度分布和電池組的適當溫度。鋰電池儲能系統中電池熱管理是保障儲能系統安全、高效運行不可或缺的單元。

以往鋰電池的熱管理技術主要針對電動汽車的動力電池，已經開發多種動力電池熱管理技術，包括主動冷卻和被動冷卻技術。主動冷卻中，電池組產生的熱量通過空氣[3-6]或液體[7-9]排出。而被動冷卻中，熱量被相變材料吸收和耗散[10-11]。

鋰電池儲能系統的熱管理與電動汽車的電池包熱管理是有密切聯系的，它們的成組結構、熱管理方式相似，各種熱管理技術也可以相互借鑒。但由于規模、使用環境、電芯類型與壽命階段不同，二者也存在差異，主要差異體現為：1）容量不同。根據標準，動力電池的容量衰減到80%后，就不能再用在新能源汽車了，而儲能的場景對電池剩余容量的要求不高，既可以用新電池，也可以利用電動汽車淘汰的電池，便于電池的梯次利用，提升經濟性。2）對溫度一致性的容忍度不同。動力電池熱管理要把最大溫差控制在4℃以內，而儲能電池熱管理系統一般要求最大溫差小于8℃[12]，這說明動力電池對電芯溫度一致性要求更高。3）熱失控的事故后果不同。電池熱失控存在“芯傳芯、模組傳模組、電池包傳電池包”的特征，動力電池包由上百個電芯組成，而儲能的電芯要高幾個數量級，且電芯容量大得多，因此規模越大，事故后果越嚴重。

在儲能電池熱管理系統中，成本較低的風冷技術是被廣泛采用的冷卻方案之一，由于空氣的熱容較小，若風冷式電池熱管理系統設計不當，可能導致電池組溫度高且溫差大。因此，需要通過系統結構設計來提高風冷式熱管理的冷卻效率。Pesaran等人[13]分別設計了具有串聯通風和并聯通風的風冷電池熱管理系統，比較了2種系統的性能，結果表明，與串聯通風相比，并聯通風的風冷系統實現了更低的溫度和更小的電池組溫差。Saw等人[14]將泡沫鋁引入風冷式電池熱管理系統中，結果表明，其可以有效降低冷卻空氣的流速，同時能保證熱管理要求的冷卻性能。Sun等人分別將錐形上冷卻管引入具有U型流[15]和Z型流[16]的平行風冷式熱管理系統中，以減少電池組的最大溫度變化。Lu等人[17]研究了供氣策略對交錯排列電池組熱性能的影響，結果表明，與Z型氣流相比，U型氣流供氣策略的電池芯的最高溫度和最大溫差均降低了3.0 K。Shahid等人[18]通過添加進氣室，降低了簡單電池組中的最高溫度并改善了溫度均勻性。Hong等人[19]基于具有Z型流的熱管理，將二次通風口引入會聚腔，以減少電芯之間的溫差。Park[20]在風道上增設一個開口與排風管相結合，以實現電池組的低電池溫度和小電池溫差。Chen等人[21]使用牛頓法優化了具有Z型流的電池熱管理系統的入口腔室(發散腔)和出口腔室(收斂腔)的幾何結構，結果表明，優化后電池的最大溫差顯著降低。隨后，還對具有U型流的熱管理系統進行了類似的優化[22]。白帆飛等人[23]使用正交試驗方法設計空間衰減范圍、發散腔和收斂腔的角度，獲得了滿足電池組最大溫度和最大溫差要求的優化熱管理系統。Xie等人[24]采用正交試驗法來優化進氣角、排氣角和等通道寬度。優化結果表明，最高溫度和最大溫差分別降低了13%和30%。Severino等人[25]將數值方法與多目標粒子群方法相結合，以優化電池的電池間距和進氣氣流的位置，結果表明，優化后電池組的最高溫度和最大溫差均降低了2℃。Chen等人[26]開發了一種優化策略，優化電芯之間的間距，以提高冷卻效率，實現了電池組最大溫差降低42%。Chen等人[27]通過優化入口和出口的位置來設計風冷熱管理系統的流型，以提高系統的冷卻效率。研究表明，入口區域和出口區域的位置顯著影響風冷熱管理的冷卻效率，當只將出口位置置于出口腔中部時，實現了最好的冷卻效率；與具有Z型流的熱管理系統相比，其最高溫度和最大電池溫差分別降低了4.5 K和7.7 K，與進出口位置均置于進出口腔室中部相比，其最大電池溫差也降低了1.7 K。

以往的研究表明，風冷熱管理系統主要采用有效的優化策略來獲得熱管理系統的優化流型，從而獲得最優的熱管理系統冷卻效率。對于儲能鋰電池，風冷熱管理系統也可通過類似優化獲得最佳的冷卻效果。

本文通過實驗和數值模擬，研究大容量儲能鋰電池單電芯的產熱特性，得出了電芯間距、進風量等因素對電芯產熱特性的影響規律。

1 數學模型

對于鋰電池傳熱模型，考慮電芯內部的熱傳導、電芯表面與空氣的自然對流換熱，而忽略熱輻射的影響。因此，電芯的溫度場T可由非穩態熱傳導方程描述：

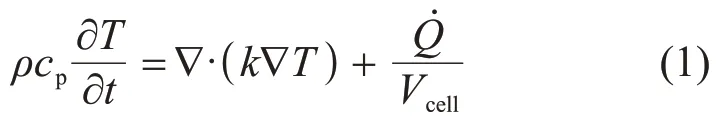
式中：t為時間，s；ρ為鋰離子電池的平均密度，kg/m3；cp為鋰電池的定壓比熱容，J/(kg·K)；k為鋰電池的導熱系數，W/(m·K)；Q?為電池產生的熱量，W；Vcell為鋰電池體積，m3。

此外，由于鋰離子電池在充放電過程暴露在空氣中，鋰離子電池的表面空氣因受電池溫度的影響而升高，溫度差的變化導致周圍空氣的流動，而空氣的流動帶走部分熱量，也會影響電池和周圍空氣的溫度。電池包內為無風力驅動源，所以可認為電池表面和空氣為自然對流換熱。為了描述空氣流場對電池散熱過程的影響，邊界條件可由牛頓冷卻定律描述：

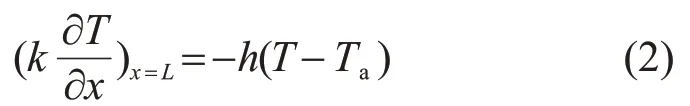
式中：x為距離，m；Ta為環境溫度，K，通常可以認為其是一個恒定不變的量；h是電池的換熱系數，W/(m2·K)；L是坐標原點到電池表面的距離。

電池產熱模型采用Bernardi均勻產熱理論，即認為電芯傳熱過程是一個發生在均一、各向異性材料中的固體熱傳導過程。為了確定電池的發熱量，采用Bernardi能量平衡方程[28]，表達式為

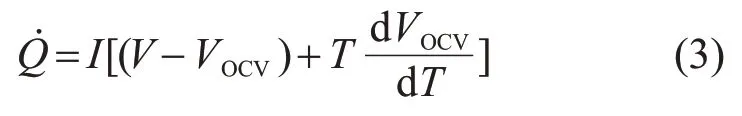
式中：V為鋰電池電壓，V；VOCV為開路電壓，V；I是工作電流，A。在式(3)中，右側的第1項是不可逆熱，包括歐姆熱和極化熱，第2項是熵變產生的可逆熱。

2 實驗研究

為提供電芯計算中的初始參數，并驗證計算結果的準確性，本文實驗測量了儲能鋰電池的導熱系數、比熱容和絕熱產熱特性。

導熱系數是按照GB/T 10297—2015《非金屬固體材料導熱系數的測定——熱線法》進行測量。熱線法是測定材料導熱系數的一種非穩態方法，其原理是在勻溫的各向同性均質試樣中放置一根電阻絲，即所謂的“熱線”，當熱線以恒定功率放熱時，熱線及其附近試樣的溫度將會隨時間升高。根據其溫度隨時間變化的關系，可確定試樣的導熱系數。實驗中，將試樣與測量探頭的組合體置于加熱爐內，把加熱爐內溫度調至測定溫度，當焊在熱線中部的熱電偶輸出每5 min的變化小于0.1 K，且試樣表面的溫度與焊在熱絲上的熱電偶的指示溫度的差值在熱線最大溫升的1%以內時，即認為試樣達到了測定溫度。測量熱線的加熱功率(電流I和電壓U)時，加熱時間達到預定測量時間5 min即切斷加熱電源。每一測量溫度下，重裝測定探頭測定3次，取平均值。

比熱容是采用加熱法進行測量，采用加熱片對電池進行加熱，則有

式中：Q為加熱量；m為被加熱物體質量；ΔT為被加熱體溫升。根據式(4)，加熱量、被加熱物體質量和溫升都可以測出，因此可以獲得電池的比熱容。進行3次實驗，取平均值作為測量結果。

絕熱產熱特性測量在加速量熱儀ARC EV+中完成。鋰離子電池充放電過程往往伴隨著熱量的產生，如果熱量不能夠及時從體系中轉移到環境中，隨著充放電循環的進行，熱量將在體系中積聚，溫度會不斷升高。當溫度升高到內部隔膜熔融，正負極會短路，將有可能產生熱失控，導致發生爆炸等事故。常規測試方法沒有考慮空氣中的散熱，加速量熱儀可以提供一個近似絕熱的環境，研究鋰離子電池在沒有熱擴散環境下的產熱規律，因此絕熱產熱的測量對電池熱安全性和熱管理工作至關重要。實驗中將鋰離子電池置于儀器的量熱腔中，外接充放電設備，可以實現在絕熱環境中對充放電過程中的溫度變化進行測定。測試條件為0.5 C充電(C為充電/放電的倍率)，環境溫度22℃，測試中充電過程為140 A恒流充電至3.65 V后靜置30 min，放電過程為140 A恒流放電至2.5 V后靜置30 min。

3 結果分析與討論

3.1 實驗和仿真模型驗證

實驗測得電池沿電池寬度、深度和高度方向的導熱系數分別為0.923、0.911、19.375 W/(m·K)，實驗測得的電池在環境溫度為22～60℃下的平均定壓比熱容為cp=1.02 kJ/(kg·K)。

圖1、2分別為電池在0.5 C、環境溫度22℃下的充電和放電過程的絕熱溫升曲線。結果表明，在充電過程中，工況時長為Δt=7 806 s，開始溫度為T0=21.993℃，最高溫度為Tf=43.258℃，絕熱溫升為ΔT=21.265℃，全過程平均發熱功率為P=15.07 W。在放電過程中，工況時長為Δt=7 635 s，開始溫度為T0=21.660℃，最高溫度為Tf=40.742℃，絕熱溫升為ΔT=19.082℃，全過程平均發熱功率為P=13.86 W。

采用上述數學模型，對單電芯的絕熱溫升特性進行了數值模擬，結果如圖1和圖2中的紅色實線所示。圖1、2中實驗與數值仿真獲得的溫度值的最大誤差為1.32℃，均方根誤差為0.62℃。儲能電池系統中可以接受的溫度估計誤差沒有一個標準值，但根據儲能系統熱管理目標是電池最大溫升≤15℃，最大溫差≤8℃，且電池管理系統(battery management system，BMS)控制風扇啟停的溫升是2℃，這個計算誤差是可以接受的。從圖1、2可以看出，充放電過程的數值模擬結果與實驗結果都吻合良好。這說明本文采用的數值計算模型和采用的相關物性參數、電化學特性參數是合理的。

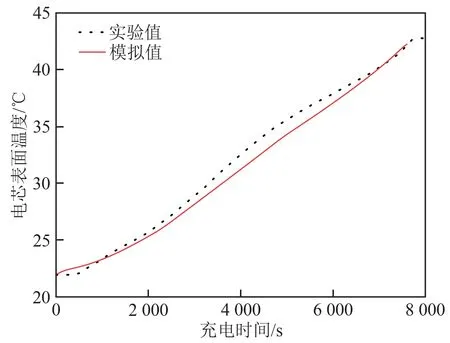
圖1 在0.5 C充電、22℃下的實驗與仿真溫度值對比Fig.1 Comparison of temperature between experiment and simulation under the condition of 0.5 C charging with ambient temperature of 22℃

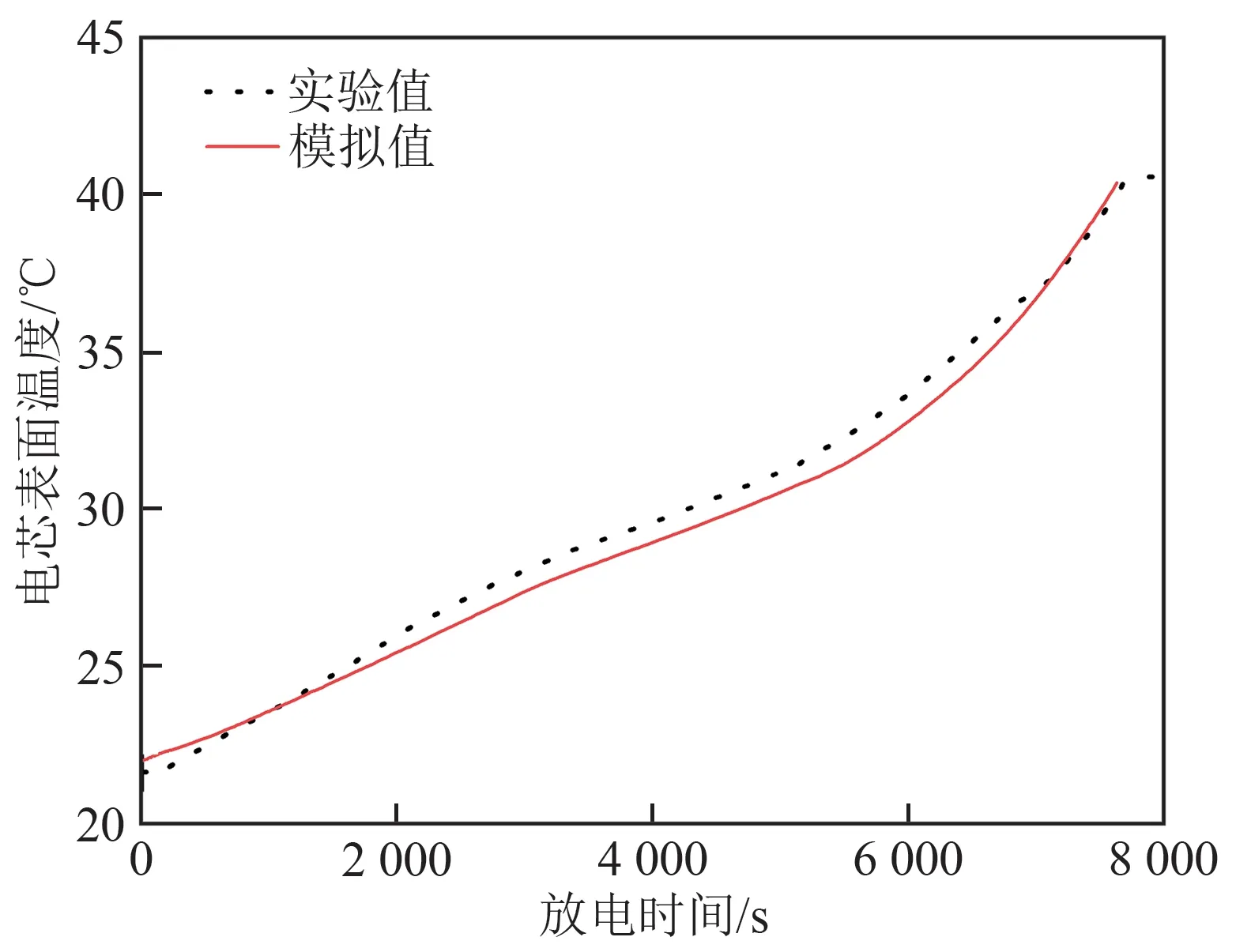
圖2 在0.5 C放電、22℃下的實驗與仿真溫度值對比Fig.2 Comparison of temperature between experiment and simulation under the condition of 0.5 C discharging with ambient temperature of 22℃

3.2 單電芯產熱特性數值模擬

在上述實驗和模型驗證基礎上，本文開展了單電芯產熱特性的數值模擬研究，研究了單電池的產熱特性，以及將2個半電池組合在一起計算時電芯間距、進風量等因素對電芯產熱特性的影響規律。

在無風情況下開展單電芯在不同工況下的產熱特性研究，分別在0.25 C、0.5 C和1 C的倍率下進行充電和放電，充放電的電池初始溫度均為環境溫度22℃。值得注意的是，本文數值模擬中不同充放電倍率用到的參數(如比熱容、導熱系數等)保持一致。計算結果如圖3、4所示，可以看出，充電和放電過程中，電芯側面中心點溫度隨著充電和放電倍率增大而升高，相應地，電池產熱量隨充放電倍率增大而增大，成正相關關系。從理論和實驗來看，大部分情況下對于小容量的動力電池來說(如18650的NCM鋰離子電池)，充電過程產熱量小于放電過程產熱量[29]，然而通過對本文實驗數據(圖1、2)和數值模擬結果(圖1—4)的分析發現，對于大容量的儲能電池來說，充電過程產熱量略高于放電過程產熱量，實驗得到的絕熱產熱特性結果表明，充電過程中單電芯平均產熱量為14.83 W，而放電過程中單電芯平均產熱量為13.82 W。

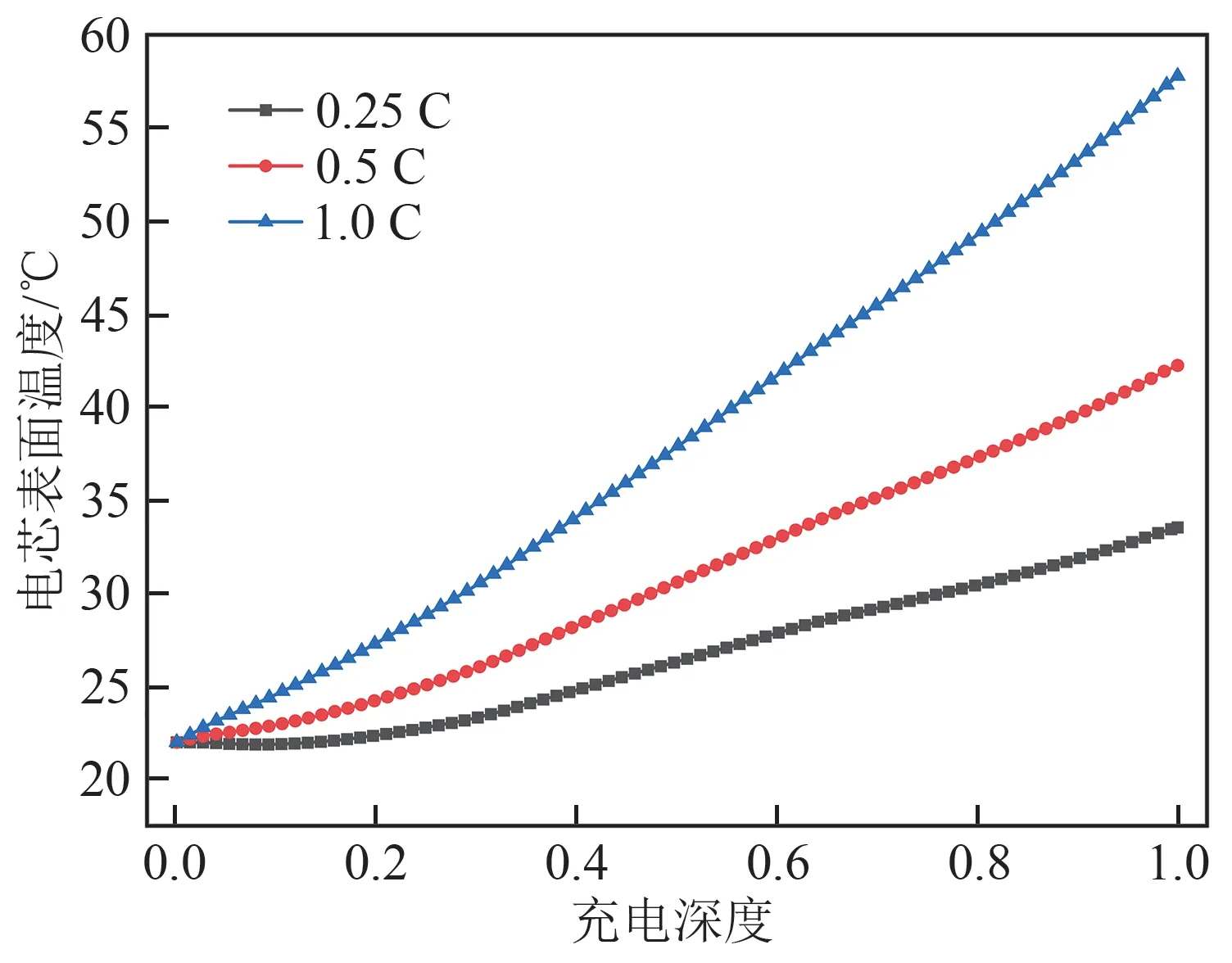
圖3 不同充電倍率下表面溫度的變化關系Fig.3 Change relationship of surface temperature under different charging rates

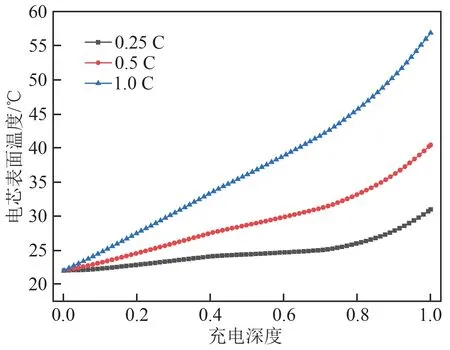
圖4 不同放電倍率下表面溫度的變化關系Fig.4 Change relationship of surface temperature under different discharging rates

圖5給出了不同充電或放電倍率下，充電或放電結束時的最高溫度及其溫升。從圖5可以看出，充電或放電過程結束時，電池最后達到的最高溫度隨著充、放電倍率的增大而增大，電池最后的溫升也是隨著倍率的增大而增大。但不管是最高溫度還是溫升，在各倍率下，充電過程相應的數值都要高于放電過程。圖5中，在充電倍率為0.25 C時，充電過程的最高溫度為33.5℃，最大溫升為11.5℃。而在充電倍率為1 C時，最高溫度可達到56.7℃，最大溫升達到34.7℃。

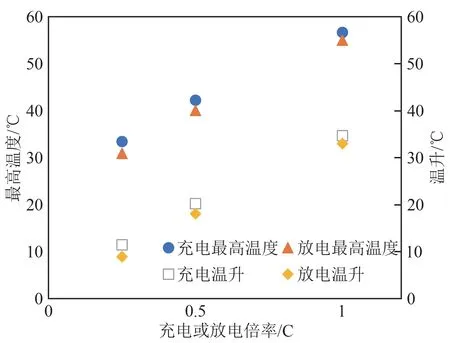
圖5 充電或放電過程結束時電池的最高溫度和溫升隨充電或放電倍率的變化關系Fig.5 Change relationship between the maximum temperature and temperature rise of the cell at the end of the charging or discharging process and the charging or discharging rates

此外，圖3的數值模擬結果還表明，在低倍率(0.25 C)充電條件下，開始階段，由于反應吸熱較多，充電過程一開始可能出現短暫的吸熱現象，表現出短暫的溫度下降的現象。

計算結果還表明，電池產熱量與溫升成正比，而圖5結果表明，溫升與充、放電倍率成正比，可見電池產熱量并不與電流的二次方成線性關系，因為電池產熱量并非僅僅是歐姆熱，而是由歐姆熱、極化熱、反應熱等部分組成，因此，產熱曲線表現較為復雜，但其與溫度分布曲線一致。

圖6給出了環境溫度為30℃時，充電過程中電芯表面溫度隨時間的變化規律。從圖6的數值模擬結果可以看出，隨著充電的進行，電芯表面溫度逐漸升高，但在任一時刻，正負極極柱附近溫度最高，這一結果與本文單電芯實驗結果一致，實驗中測量溫度也顯示極柱處溫度比側壁面溫度高2～3℃。計算結果表明，在充電結束時，電池最高溫度為47.4℃，最低溫度為41℃，其最大溫差為6.4℃。

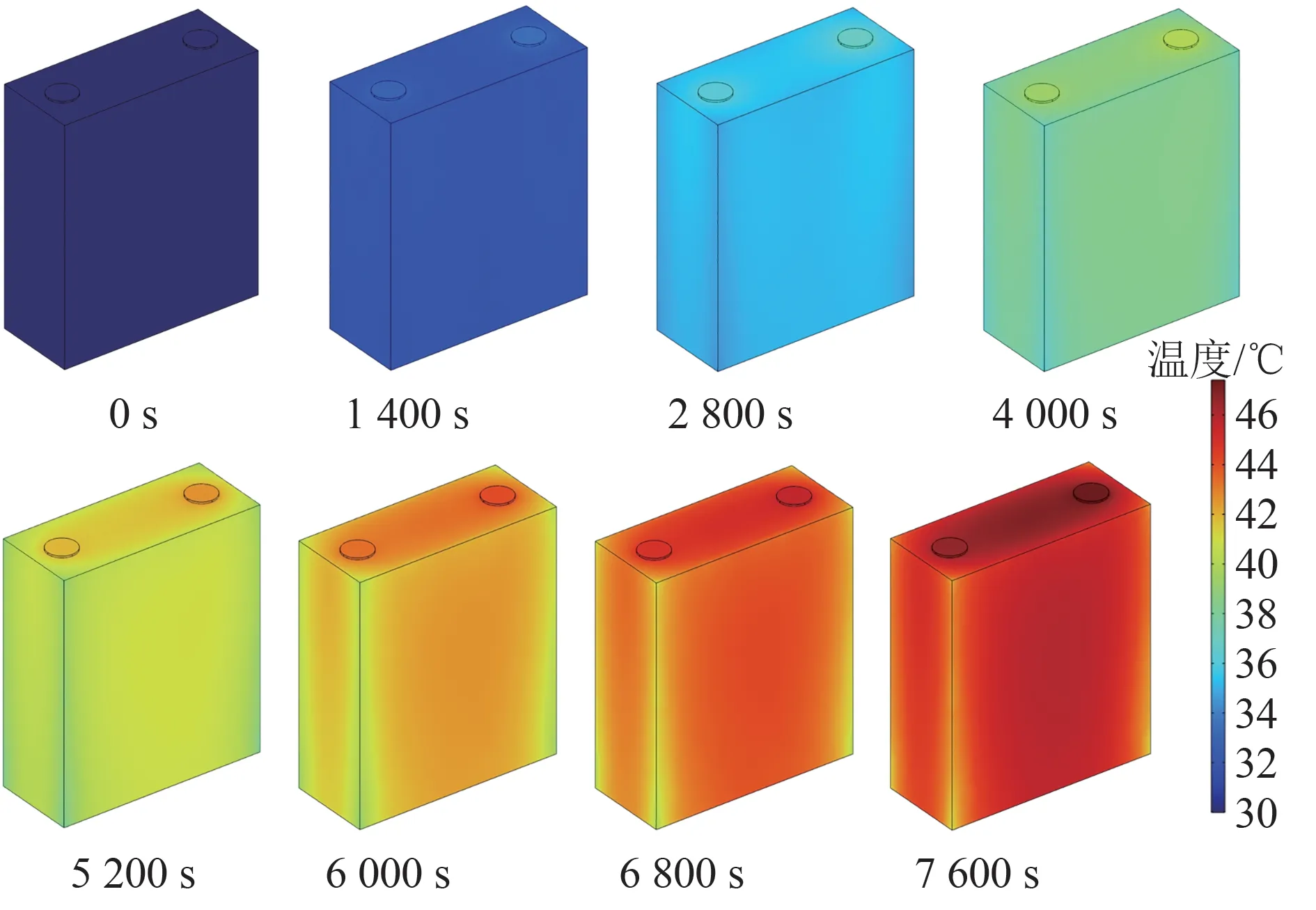
圖6 充電過程中電芯表面溫度隨時間的變化Fig.6 Change of cell surface temperature with time during charging

為考慮冷卻進風量對電芯產熱的影響，在單電芯計算時，考慮相鄰電芯之間有通風及通風通道存在，計算時相鄰2塊電芯各取一半，這樣組成一個電芯的計算區域，該計算域由2塊半電池與前部、后部、上部以及2塊電池中間的空氣域組成。此時，相鄰2個電芯之間的通道可以用于考慮冷卻進風對電芯發熱特性的影響規律。據此也可用于研究2個半塊電池間的間距對電池產熱特性的影響，當這個間距發生變化時，空氣通道的面積也會發生變化，因此空氣流速也會發生變化，進而電池與空氣的對流換熱會發生變化。圖7、8分別給出了充電和放電結束時電芯和流體區域的溫度分布和速度分布，圖中溫度場與速度場是在0.5 C倍率、初始溫度20℃、進風溫度20℃、進風量0.002 kg/s下獲得的放電特性。

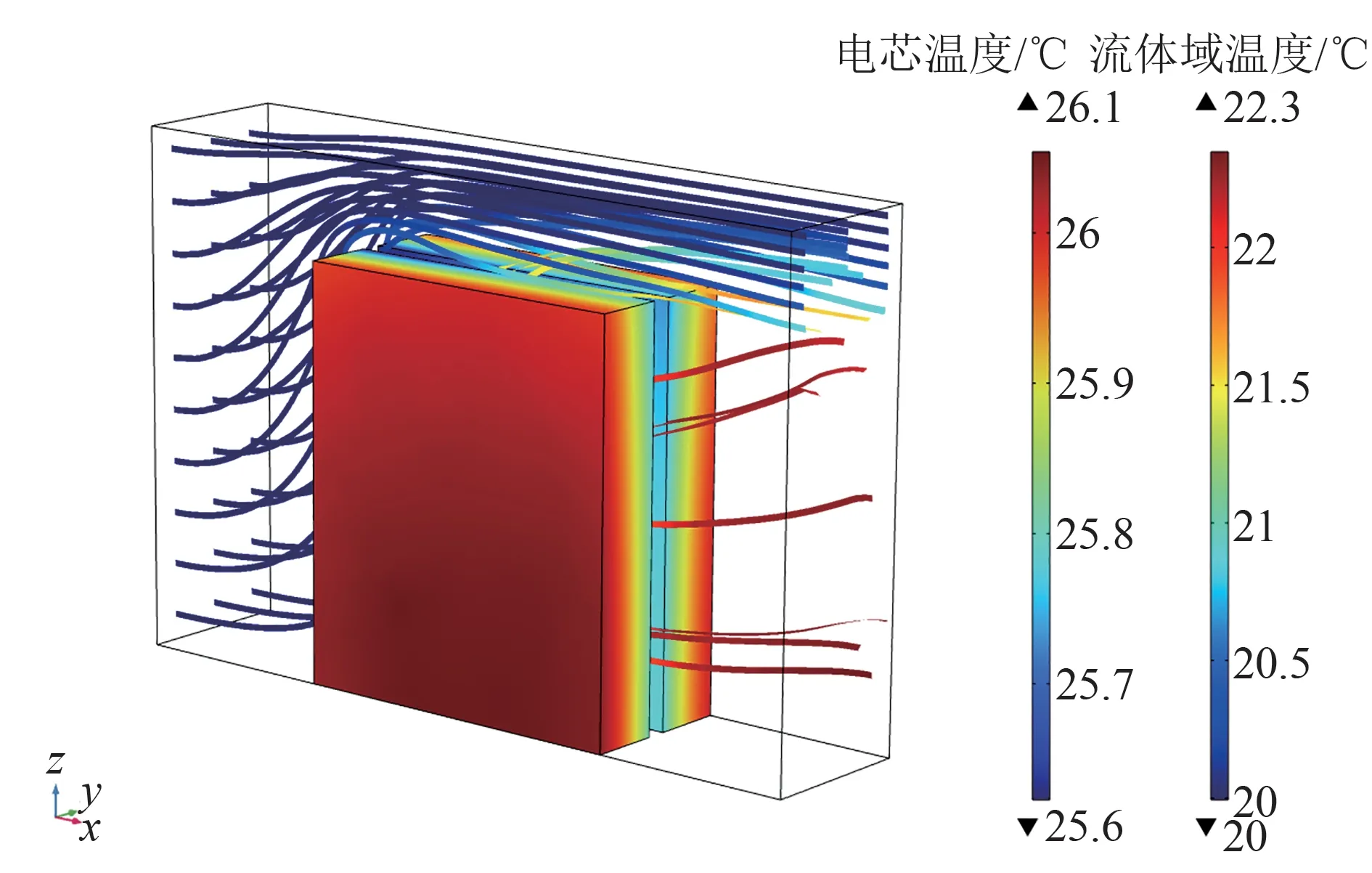
圖7 放電結束時電芯和流體域的溫度場Fig.7 Temperature profiles of cell and fluid domain at the end of discharge

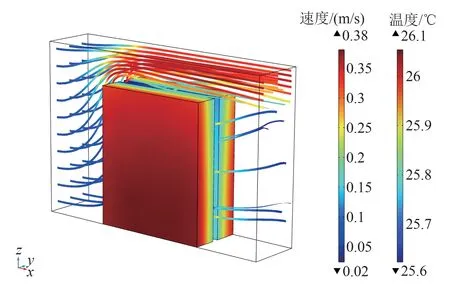
圖8 放電結束時流體域速度場與電芯溫度分布Fig.8 Velocity in fluid domain and cell temperature distributions at the end of discharge

計算結果表明，隨著電池間距的增加，電池表面流速降低，強迫對流換熱程度減弱，冷卻效果降低，電池的最低、最高和平均溫度都隨著間距的增大而逐漸升高，但是電池的最大溫差隨著間距的增大而逐漸降低。

圖9給出了不同間距下完成充電時刻的電池間空氣中心處流速與溫度的分布。可以看出，電池間距對流道中流速的影響有一個臨界值，低于該值時，隨著電池間距的增大，電池間空氣流速稍有增大；大于該臨界值后，隨著間距的增大，空氣流速減小，且減小的趨勢近似于線性變化。而空氣溫度隨著電池間距的增大迅速減小，間距大于臨界值后，隨著電池間距增大，通道中心處空氣溫度減小趨勢變緩，溫度幾乎保持不變。

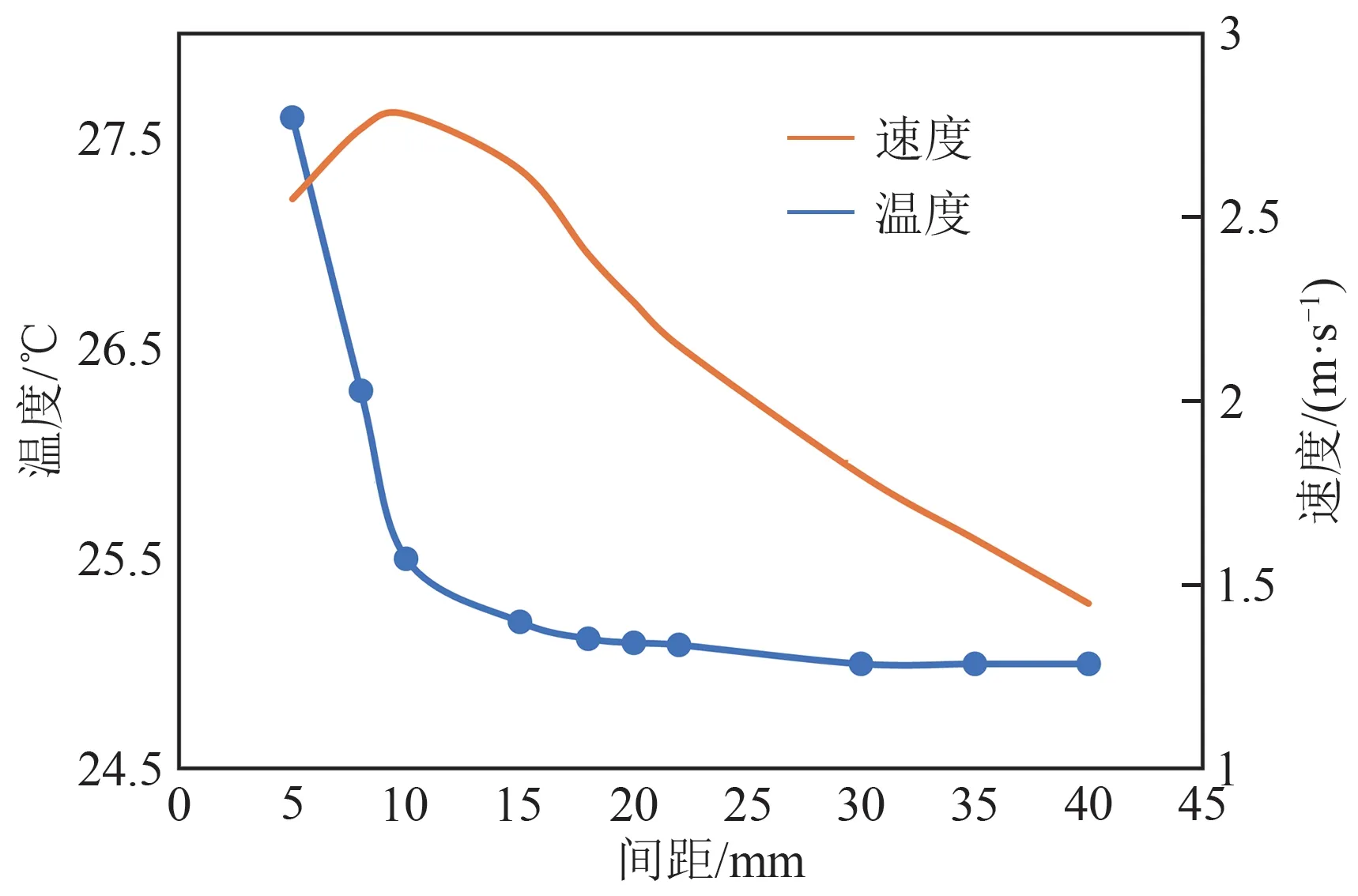
圖9 不同間距下電池間空氣中心處流速與溫度分布Fig.9 Flow velocity and temperature distributions at the center of the channel between cells under different spacings

進一步的計算結果如圖10所示，隨著電池間距增大，電池側壁面的溫度隨著間距的增大表現為先降低后增加的趨勢。

類似地，電池間距對迎風面、頂部、背風面溫度的影響均呈現出先降后增的趨勢，與間距對電池側壁溫度的影響是一致的。這表明，存在一個最佳電池間距，在該間距下，能使得電池側壁溫度最低，通道中空氣流速相對較大，空氣溫度相對較低。在本文算例中，綜合圖9和圖10可看出，當間距位于10～20 mm時，電池間中心處空氣流速較大，同時空氣溫度和電池側壁面溫度較低，所以該間距即為最佳間距。

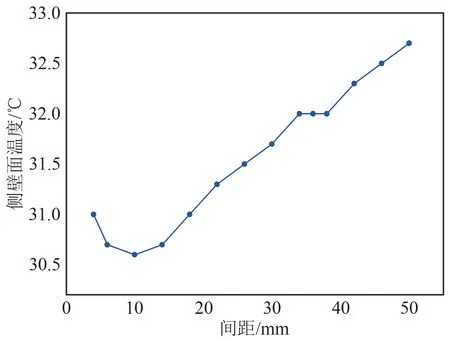
圖10 側壁面溫度與電池間距的變化關系Fig.10 Change relationship between the side wall temperature and the battery spacing

在保持電池間距和進風溫度不變的情況下，進風量對電池產熱也有較大的影響。數值模擬結果表明，不論充電結束還是放電結束時，電池的最高溫度、最低溫度和平均溫度隨著進風量的增大均呈現降低趨勢，而最大溫差則隨進風量增大而上升，但總的溫差都很低，低于2℃。同時計算結果表明，在進風溫度不變條件下，考慮到電芯合適的工作溫度為25℃，此時都可以獲得一個最佳的進風量，其與進風溫度的變化關系如圖11所示。

計算中，采用正交法設置計算參數，即以電芯合適的工作溫度(25℃)為計算目標，分別在進風溫度18、20、22、24℃的條件下，改變進風量，進行一系列的數值計算。例如，進風溫度為18℃時，計算一系列的進風量數值，改變進風量，直到電芯溫度在工作結束時大約在25℃，此時的進風量即為最佳進風量。同理計算進風溫度為20、22、24℃的條件下，最佳進風量與進風溫度的變化關系。從圖11可以看出，隨著進風溫度的增大，為使電池工作在合適的溫度(如25℃)附近，需要的進風量呈幾何倍數升高，因此，通過采用合適的進風溫度，從而選擇合適的進風量，是儲能電池柜熱管理中需要優先考慮的事情。這樣可以在保證冷卻效果的前提下，實現功耗的最低化。在本文的計算條件下，當進風溫度為18℃時，選取1 g/s的進風量是最優的。

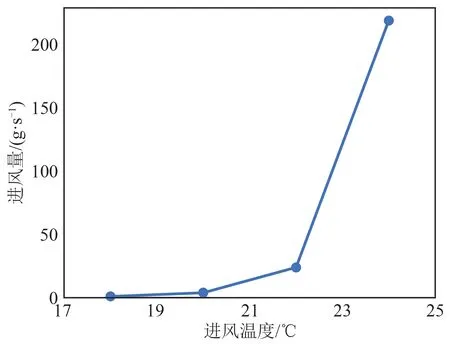
圖11 最佳的進風量與進風溫度的變化關系Fig.11 Change relationship between the optimal inlet air flux and inlet air temperature

4 結論

采用實驗和理論的方法研究了某型大容量儲能鋰電池單體的傳熱特性，獲得如下結論：

1）電池沿電池寬度、深度和高度方向的導熱系數分別為0.923、0.911和19.375 W/(m·K)；電池在環境溫度為22～60℃下的cp=1.02 kJ/(kg·K)。實驗獲得了充電和放電過程的絕熱溫升曲線。

2）實驗與數值模擬獲得的溫度值最大誤差為1.32℃，均方根誤差為0.62℃，數值結果與實驗結果吻合良好，驗證了所建立電芯傳熱模型的可靠性。

3）對于大容量的儲能電池來說，充電過程產熱量略高于放電過程產熱量。充電和放電過程中電池最后達到的最高溫度、最大溫升隨著充放電倍率的增大而增大。

4）最佳電池間距是10～20 mm，在該間距下能使得電池側壁溫度最低，通道中空氣流速相對較大，空氣溫度相對較低。

5）當進風溫度為18℃時，選取1 g/s的進風量是最優的。