裝配式建筑PC構件車輛調度優化
蒲坤俏, 萬 鵬,2*
(1.青島理工大學 管理工程學院, 山東 青島 266525;2.青島理工大學 智慧城市建設管理研究中心, 山東 青島 266525)
0 引 言
以現澆為主體的傳統建造模式施工效率低下,存在嚴重的資源浪費和環境污染問題,與我國倡導的綠色發展理念相背離。
近年來,政府大力支持裝配式建筑發展,以降低資源環境壓力,提高勞動生產效率。
裝配式建筑所需的預制構件(Precast Concrete, PC)是工廠采用標準化方式生產,可減少不必要的材料浪費,更加節材環保,且減少了施工現場人員的配備,在用工成本和安全生產方面都有較大改進[1]。為了控制裝配式建筑建造成本,劉煒[2]通過對比分析傳統現澆模式及裝配式建筑的成本構成,得出裝配式PC構件的增量成本構成。
其中,PC構件制作人工成本、結構增量、購置稅、裝運存卸等成本較高,具有較大的優化空間。而PC構件配送成本的高低與車輛配送方案有較大關系,若對配送方案進行合理配置,可在一定程度上提高配送效率,降低配送成本。
目前,國內外針對裝配式建筑PC構件配送成本優化的研究相對較少。Chan W T等[3]針對預制構件生產調度問題,提出一種流水車間排序模型,并使用遺傳算法求解。Zhou Z等[4]設計了一種基于貪婪策略的改進遺傳算法,并應用于云環境中的任務調度優化。段海寧等[5]通過構建基于車輛油耗成本、人工成本及車輛租賃成本的成本優化模型,并改進粒子群算法,得到最優成本下的車輛配送方案。但該模型未考慮工地的時間窗約束。邵必林等[6]考慮到配送過程中可能產生的時間等待成本,并基于時間窗約束構建配送成本優化模型,最后得到最優成本下的車輛調度方案。胡曉晨[7]在此基礎上,將車輛運送過程中的道路交通阻抗因素考慮在內,并引入傳統路阻函數(BPR)模型。但該模型是通過分析美國一些低飽和流量道路所得,當城市道路處于飽和或者過飽和狀態時,模型的擬合精度較差[8]。
綜合上述分析,文中在模型構建時考慮多車型、時間窗及道路交通擁堵情況,構建PC構件配送成本優化模型,設計遺傳算法進行求解,并進行算例測算,驗證該模型的有效性。
1 問題描述與條件假設
1.1 問題描述
假設有1個預制廠F和S(>2)個施工工地,預制廠配備有專門的運輸車輛,根據載重量不同,分為λ種車型。預制廠需要根據工地配送需求,在各工地要求的時間窗(TEs,TLs)范圍內送達。在此過程中,要求設計一套合理的配送方案,使得配送總成本最小。
1.2 條件假設
為了便于研究,將實際生活中的問題轉化成可以求解的數學模型,做出以下假設:
1)配送車輛的行駛路線是提前規劃好的最佳路線,即運輸距離是已經確定的。
2)同一車型的車輛在倉庫的裝車時間、同一工地的卸車時間均相同。
3)在倉庫裝車時,同一構件一次只能向一輛車裝車。
4)在工地卸車時,一次只允許一輛車進行卸車。
5)所有配送車輛在工地卸車完成后均需在第一時間返回預制廠,并等待下一批次的配送任務。
6)配送車輛不會出現中途故障停車現象,只會因道路交通擁堵產生等待時間。
7)配送車輛的油耗量只與其載重量、運輸距離和時間有關,且成正比例關系。
2 模型構建
2.1 參數推導
車型為λ的車輛單次可運載構件數量

(1)
式中:INT----取整函數;
Bλ----λ車型載重量;
pws----單件構件重量。
車型為λ的車輛完成工地S所有訂單需求量的配送總車次數
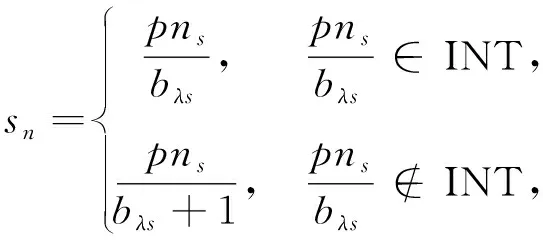
(2)
式中:pns----工地S所需構件總數量。
預制構件配送流程中涉及到的時間參數如圖1所示。
各時間參數推導如下:
1)車輛因前一車次正在裝車,而需等待的時間為
WBTsn=STsn-STsn-1-BTλ,
(3)
式中:STsn----當前車次發車時間;
STsn-1----前一車次發車時間;
BTλ----裝車時間。

圖1 預制構件配送流程時間參數
2)假設車輛在滿載時的平均行駛速度為V1,則當交通暢通無阻的情況下,從預制廠F運輸到施工工地S所需的時間為
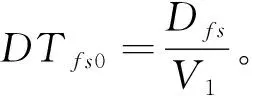
(4)
為使模型更具實際應用價值,文中考慮了車輛行駛過程中的道路交通阻抗因素。采用基于百度交通大數據計算得出的擁堵指數作為衡量城市道路交通擁堵程度的指標,更加符合不同城市的實際擁堵情況。擁堵指數計算公式為
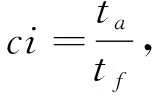
(5)
式中:ci----擁堵指數;
ta----實際通行時間;
tf----自由通行時間。
根據式(5)可以看出,實際通行時間為自由通行時間與擁堵指數的乘積,進而可求得存在道路交通阻抗因素的影響時,配送車輛從預制廠行駛至施工工地S的實際運輸時間為

(6)
3)車輛到達工地的時間點
ATsn=STsn+DTfs。
(7)
4)車輛因到達工地的時間早于時間窗約束TEs而需要等待的時間
WTEsn=TEs-ATsn。
(8)
5)車輛到達工地時,因前一車次正在卸車而需要等待卸車的時間
WUTsn=LTs,n-1-ATsn,
(9)
式中:LTs,n-1----前一車次的離開時間。
6)車輛在工地的總等待時間
WTsn=p·WTEsn+q·WUTsn,

(10)
7)車輛離開工地的時間點
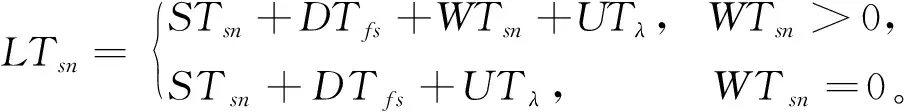
(11)
8)假設車輛返回時的空載運輸速度為V2,則當存在道路交通擁堵情況時,從工地S返回到預制廠F所需的時間為
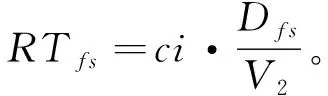
(12)
9)車輛返回預制廠的時間點
FTsn=LTsn+RTfs。
(13)
2.2 配送總成本
預制構件的配送成本可分為固定成本和可變成本。其中,固定成本主要包括配送車輛的租賃費、維護管理費、折舊費、人工費等;可變成本主要包括燃油成本,因倉庫等待裝車、工地等待卸車,在運輸途中因交通阻抗因素導致的等待時間等產生的時間等待成本,以及未按照施工工地要求的時間窗約束配送的時間懲罰成本[9-10]。
2.2.1 固定成本

(14)
式中:CF----總固定成本;
CFc----單輛車固定成本;
c----車輛數。
2.2.2 燃油成本
假設每百公里油耗量為O(L),車輛平均時速為V(km/h),則行駛一百公里所需的時間t=100 km/h,單位時間油耗量為O/t。單位時間燃油成本為
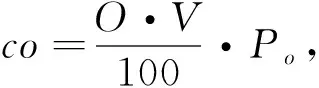
(15)
式中:Po----燃油價格。
總燃油成本
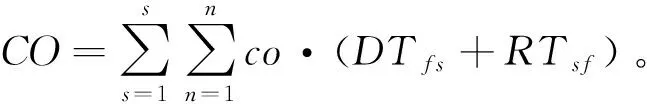
(16)
2.2.3 時間等待成本

(17)
式中:ω----時間等待成本系數。
2.2.4 時間懲罰成本

(18)
式中:β----時間懲罰成本系數。
2.2.5 配送總成本
配送總成本主要包括配送車輛固定成本CF、總燃油成本CO、時間等待成本CW和時間懲罰成本CP等。配送總成本可表示為
CT=CF+CO+CW+CP=

(19)
2.3 車輛調度成本優化模型構建
基于配送總成本最低的預制構件配送車輛調度優化模型
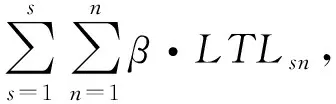
(20)
s.t.
STsn≥FT,
(21)
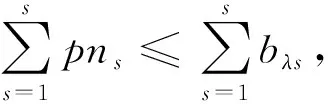
(22)
STsn-STs,n-1≥BTλ,
(23)
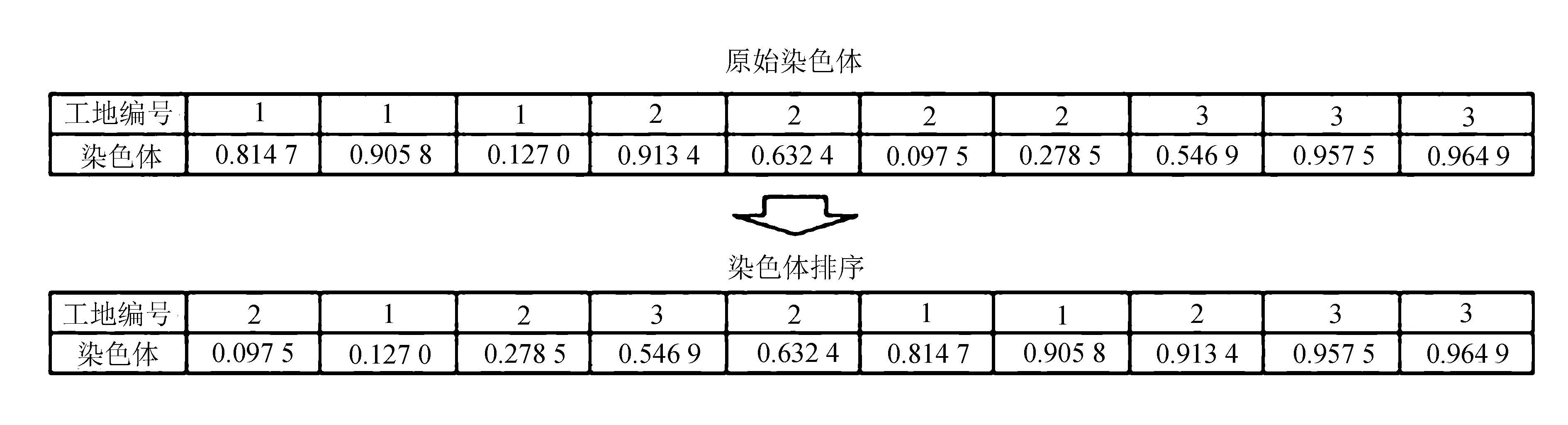
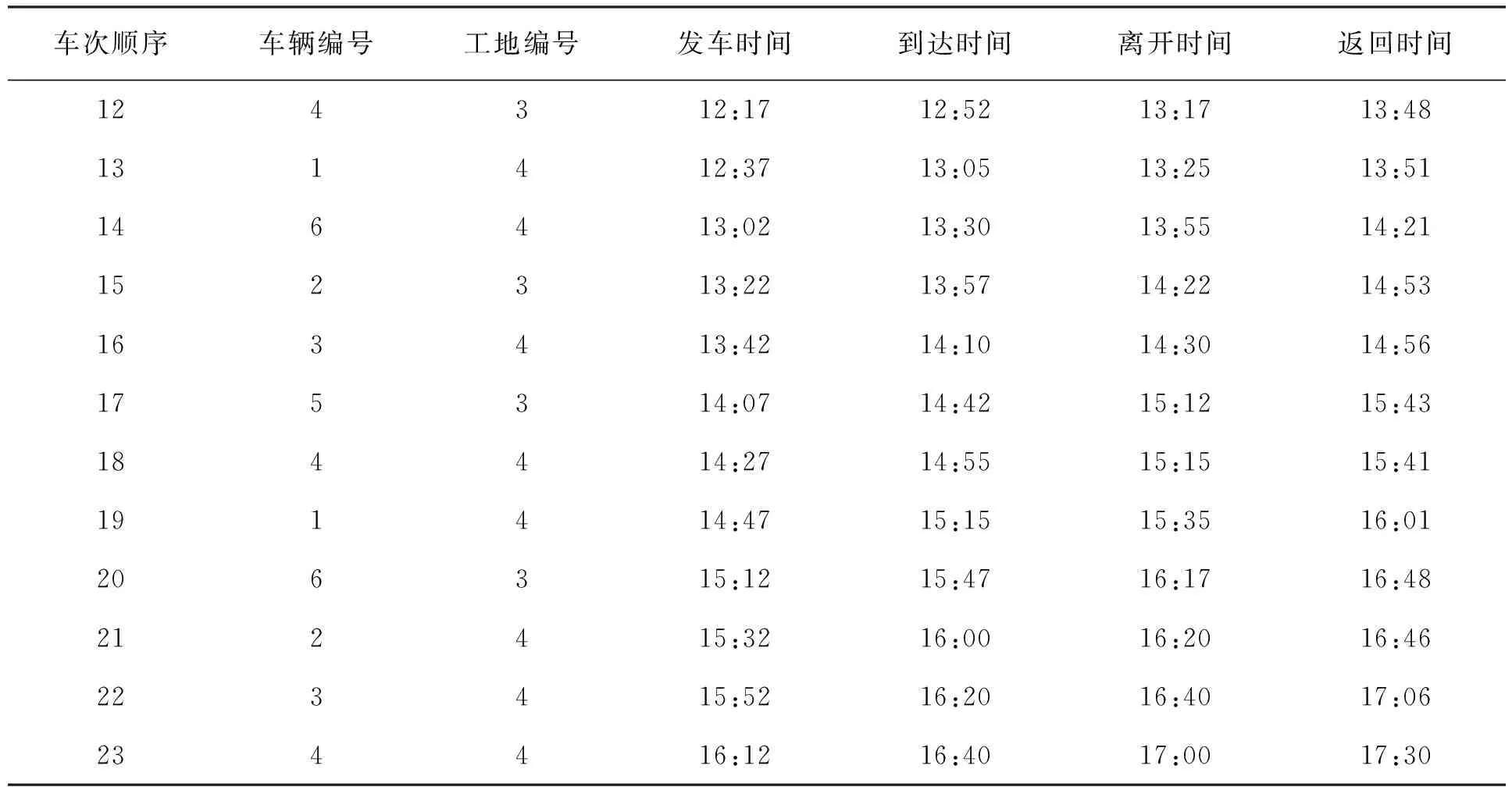
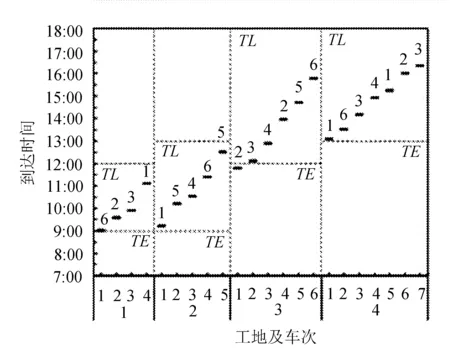
C (24) 式(21)表示車輛首次發車時間應晚于預制廠開始工作的時間FT;式(22)表示預制廠的配送數量滿足各工地對構件的需求量;式(23)表示前后兩車次發車時間間隔不小于配送車輛的裝車時間;式(24)表示預制廠的可配送車輛數小于各工地的總配送車次。 PC構件配送車輛調度優化問題是NP難問題,設計遺傳算法對該問題進行求解。遺傳算法模仿生物進化過程進行尋優,算法簡單高效[11]。首先,對需要解決的問題進行相應的染色體編碼,每條染色體便是待解決問題的一個初始解。然后,生成隨機種群,根據所研究問題的目標函數設置對應的適應度函數,以此來淘汰種群中的劣勢個體。經過選擇、交叉、變異等遺傳操作來提高種群中染色體的適應度,從中尋找適應度最高的個體[12-13]。 遺傳算法具體求解流程如圖2所示。 圖2 遺傳算法求解流程 3.2.1 初始種群編碼 將解向量編制成長度為所有工地需求車次之和的染色體。假設有3個施工工地,編號為1、2、3,工地需求車次依次為3、4、3,則染色體長度為10,染色體基因為0-1間的隨機數,染色體結構實例如圖3所示。 圖3 染色體結構實例 將染色體解碼后的發車順序為:2→1→2→3→2→1→1→2→3→3。 3.2.2 適應度計算 由于文中以PC構件配送成本最小為目標,因此,適應度函數取配送總成本的倒數表示 (25) 式中:fi----第i個個體的適應度值; CTi----第i個個體對應的配送總成本,CTi越小,適應度值越大。 3.2.3 選擇 分別計算各染色體的適應度值,采用輪盤賭方法選擇最優個體。 3.2.4 交叉 染色體采用浮點數編碼,因此選擇算數交叉,根據兩個個體的線性組合生成新個體。 3.2.5 變異 當交叉操作不能產生新個體時,通過變異算子打破局部收斂。 3.2.6 算法終止 算法達到最大迭代次數后,則輸出此時的最優解。 選取青島市某PC構件制造廠作為研究對象,此預制廠主要生產預制梁、柱、疊合板等,且生產數量滿足目前簽訂的4家施工工地的訂單需求。 施工工地需求量及時間窗約束見表1。 表1 施工工地需求量及時間窗約束 預制廠目前使用租賃運輸車輛進行配送,由于成本與規模的限制,預制廠當天可用于配送的車輛有6輛,根據載重量分為兩種車型,在進行配送車輛調度時,可在兩種車型中選擇并自由匹配,以期達到最低的配送成本。車輛滿載時的時速為50 km/h,空載時的時速為55 km/h,柴油當時的市場價格為6.8 元/L。兩種車型的相關參數信息分別見表2和表3。 表2 車輛基本信息 表3 不同車型油耗及單位時間燃油成本 配送車輛按照提前規劃好的最佳配送路線對施工工地進行配送,配送過程中可能會遇到交通擁堵的狀況,該市非高峰期平均擁堵系數為1.08,高峰期(7:00-9:00, 17:00-19:00)平均擁堵系數為1.25。 根據預制廠至施工工地的距離,不同車型的性能參數,以及道路擁堵指數等信息,計算出預制廠至施工工地的運輸時間及返回時間,計算結果見表4。 表4 預制廠至施工工地距離及時間信息 4個施工工地對應的單位時間懲罰成本系數β為16元/min,單位時間等待成本系數ω為2.5元/min。 將上述工地需求信息及車輛信息輸入到根據模型編寫好的代碼中,采用Matlab軟件進行求解。設置遺傳算法的相關參數為:種群規模N=50,交叉概率Pc=0.9,變異概率Pm=0.05,算法達到最大迭代次數100次后終止運行,并輸出最優結果。 遺傳算法最終計算得出的最低配送總成本為1.065 8萬元,未優化前的總成本為1.159 4萬元,優化后的方案成本降低8.07%,節省936元。系統運行得到的總成本收斂圖如圖4所示。 由圖4可以看出,此算法具有良好的收斂性能,對模型的求解效果較好。 圖4 配送成本收斂圖 根據遺傳算法求解模型程序命令窗口中輸出的結果,對應整理可以得到總配送成本最低時的車輛出車順序,以及每車次的發車時間,配送車次時間表見表5。 表5 配送車次時間表 續表5 由表5計算結果可以看出,第1車次為編號6的Ⅱ型車8:15出發,發往施工工地1,到達工地的時間剛好為時間窗約束的開始時間9:00,卸車時間花費35 min,10:11返回預制廠;該車輛第二次發車時間為10:52,發往工地2。第2車次為編號1的Ⅰ型車8:35出發,發往施工工地2,到達工地的時間為9:13,卸車時間花費25 min,10:07返回預制廠;該車輛第二次發車時間為10:27,發往工地1,到達工地的時間為11:06。其他情況不再一一列舉。 文中從施工工地的視角出發,繪制車輛到達施工工地的時間分布圖,如圖5所示。 圖5 車輛到達時間分布圖 通過對比各車次的到達時間與施工工地的時間窗約束可以發現,除工地3的第一車次車輛到達時間略早于工地最早接車時間外,其余車次均在時間窗范圍內,說明該調度方案完全滿足施工工地對于預制構件送達及時性的要求。 該配送時間表在滿足施工單位時間窗要求的前提下,同時考慮了多車型及運輸途中的道路交通阻抗情況,派往各工地的發車順序及時間節點清晰明了。 通過本模型還可輸出對應車次的燃油成本、時間等待成本和時間懲罰成本。該模型有利于配送管理人員進行科學的調度管理,避免憑借經驗進行車輛安排及一味滿足各施工工地需求,而忽略配送過程中額外成本支出的情況,具有良好的適用性。 針對我國裝配式建筑PC構件配送成本優化問題,從預制廠的角度出發,綜合考慮各施工工地的時間窗約束、道路交通阻抗、多種車型等因素,構建由固定成本、燃油成本、時間等待成本以及時間懲罰成本等四部分組成的預制構件配送總成本優化模型,并設計遺傳算法進行求解。通過算例分析,驗證了模型和算法的有效性,模型可以有效地反映出PC構件在實際配送過程中的各類成本支出,能夠得到配送總成本最低時的配送車輛調度方案及清晰的配送時間表。從而為預制廠的車輛調度工作提供決策依據。3 遺傳算法模型
3.1 遺傳算法原理
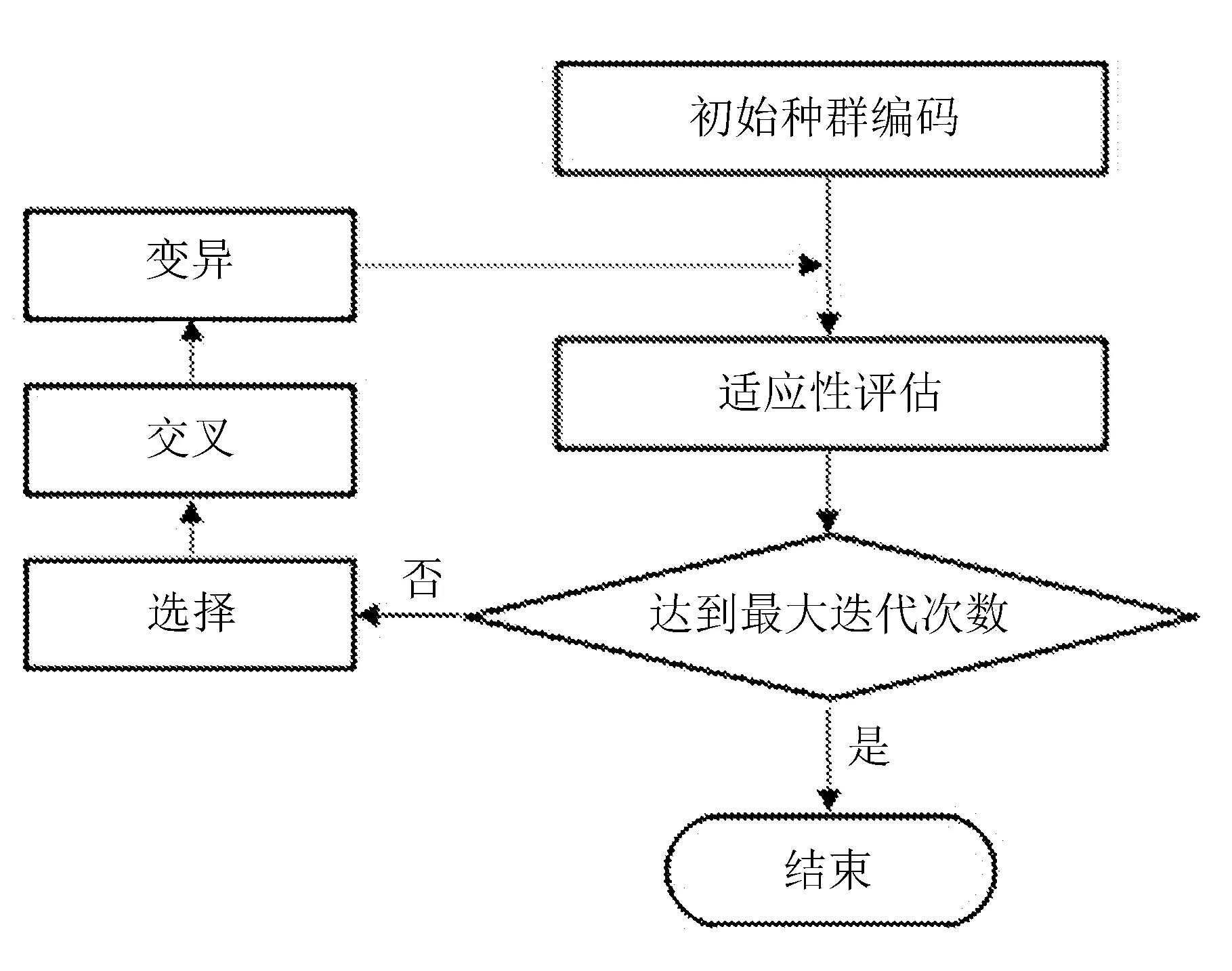
3.2 遺傳算法求解步驟
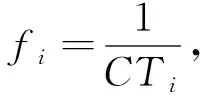
4 算例分析
4.1 算例信息描述
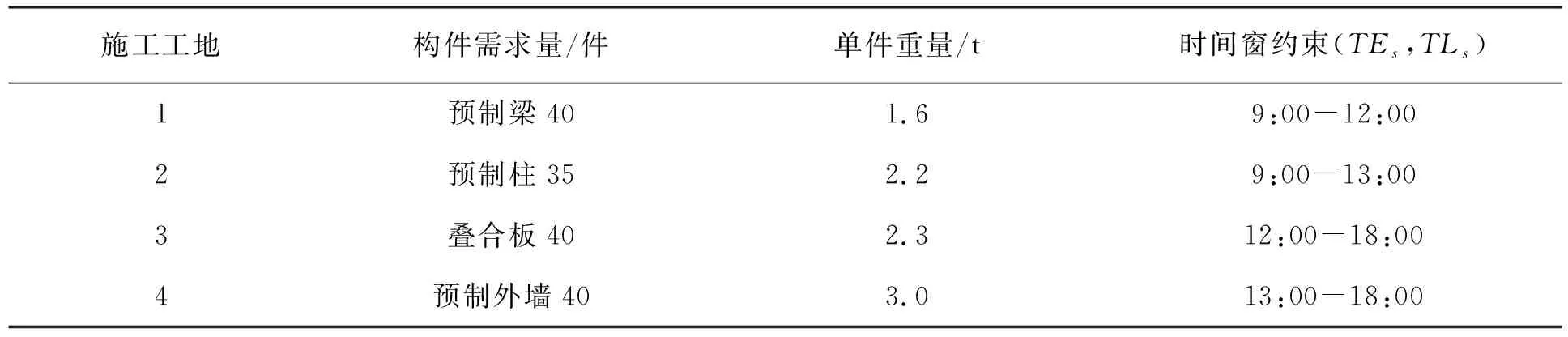


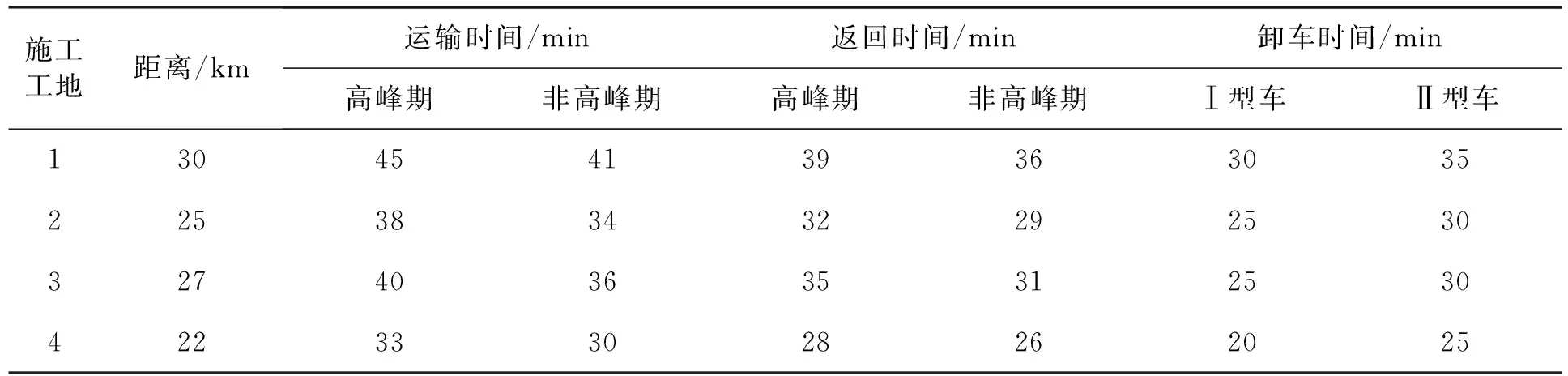
4.2 遺傳算法求解
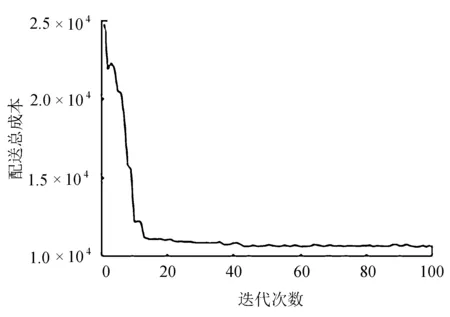
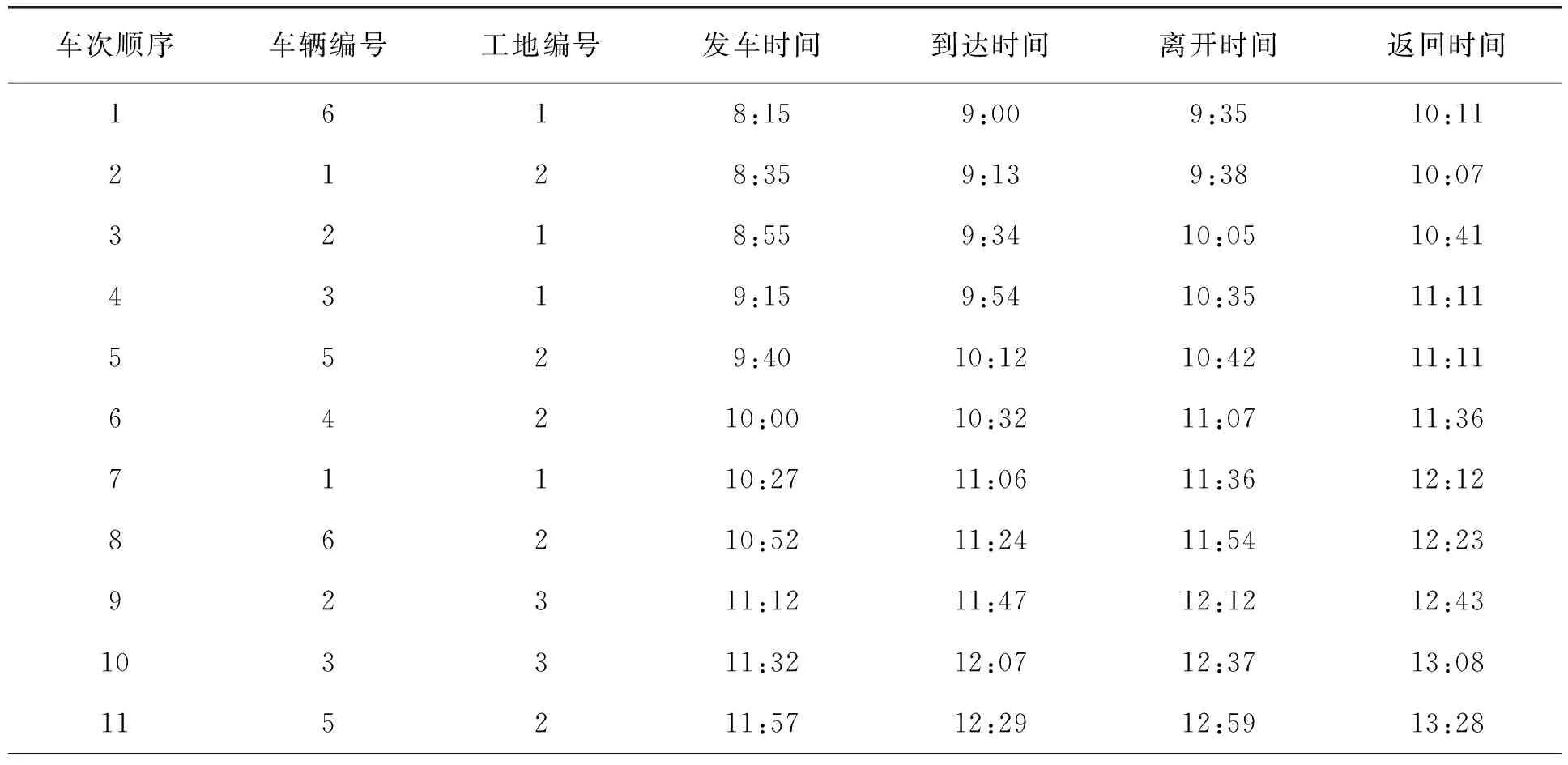
5 結 語

