基于多場耦合能量和熵產分析的礦用雙盤式磁力耦合器參數多目標優化

王 爽，郭永存，李德永，程 剛，馬 鑫

(1.安徽理工大學 深部煤礦采動響應與災害防控國家重點實驗室，安徽 淮南 232001；2.安徽理工大學 機械工程學院，安徽 淮南 232001)

雙盤式磁力耦合器是一種采用非接觸方式傳遞動力的新型調速裝置[1]，具有輕載啟動、過載保護、隔離振動、零泄露、節能環保等特性[2]，與傳統的機械聯軸器、液力耦合器等傳動裝置相比，磁力耦合器的調速性能更高效、大功率傳動更可靠，惡劣環境適應性更強、運行成本更低，因此適用于煤礦惡劣的工作環境[3]。近年來已逐漸成為礦山機械裝備傳動系統的重要組成部分[4]。

電磁-溫度-應力耦合能量作用是一個相當復雜的問題，已成為磁力耦合領域的熱點課題之一[5]。雙盤式磁力耦合器運轉時，由于導體銅盤內電阻的存在，銅盤內生成的感應渦流會有一部分轉化成熱能，造成磁力耦合器內的溫度升高。當溫升高達一定值時，會導致永磁材料的剩余磁感應強度快速下降，從而磁力耦合器所能傳遞的力矩降低，影響其正常工作[6]。BADICS Z等[7]針對非線性單向耦合電磁熱問題，提出一種自適應時間積分算法，通過對感應淬火問題和絕緣柵雙極晶體管測試模塊的熱分析，說明了該算法的有效性；MAKNI Z等[8]采用耦合的電磁-熱模型分析了永磁電機，降低了設計過程的耗時并提高可靠性；KIM D S等[9]提出了一種電磁-熱耦合三維有限元分析法，測量了實際模型的電流波形和溫度變化，根據模型的形狀和電流波形進行了有限元建模；ECKERT P R等[10]提出了一種考慮幾何和溫度約束的熱耦合和電磁耦合的線性致動器的設計方法，該方法使力密度最大，力紋波最小；ELKALSH A等[11]提出了一個耦合的電磁-熱模型，并通過非線性和色散等離子體材料模型耦合，分析了耦合電磁熱模型的穩定性和精確性。國內學者也對磁熱耦合方法開展了一些研究，胡云鵬等[12]在電流幅值最大為 1 500 A 時，求解空心電抗器周圍磁場分布以及輸出柜的渦流損耗，將渦流損耗作為主要的熱源，根據電磁學和熱力學理論建立電抗器的三維磁熱耦合有限元模型；葛研軍等[13]設計了一種外轉子為永磁轉子而內轉子為銅套轉子的磁耦，通過對渦流損耗進行理論分析與仿真計算，驗證了永磁體極數及氣隙長度對渦流損耗的影響；王雷等[14]提出一種基于流固耦合速度場計算散熱系數進而分析耦合器溫度場的方法，并進行三維溫度場數值模擬，得到耦合器溫度場分布；張河山等[15]將計算得到的繞組銅耗、定子鐵芯損耗、永磁體渦流損耗以及雜散損耗等作為熱源，采用磁熱耦合法將其耦合到各部件進行瞬態溫度場研究。

熵產分析的目的是使系統的做工損失降到最小，使系統所做的有用功最大化，降低熵產可提高系統的傳動效率[16]。然而上述的諸多研究中僅單一考慮通過多場耦合能量分析雙盤式磁力耦合器的散熱問題，多數研究并未將其與熵產有效結合，僅是將一方面作為優化目標是不全面的[17]，增加散熱量的同時會造成系統熵產值的增大，因此這也是雙盤式磁力耦合器參數優化的難點，如何在保證散熱量的前提下盡可能降低系統的熵產值。為此本文針對礦用雙盤式磁力耦合器的散熱量和熵產，以熱力學模型為基礎，采用有限元法模擬傳動過程，以獲取散熱量與熵產；采用人工蜂群算法(Artificial Bee Colony，ABC)優化的高斯過程回歸方法(Gaussian Process Regression，GPR)構建有限元仿真的代理模型，并采用多目標粒子群優化算法(Multi Objective Particle Swarm Optimization，MOPSO)獲取最優參數。

1 雙盤式磁力耦合器的熱力學模型

1.1 工作原理

雙盤式磁力耦合器主要由輸入軸、銅盤、永磁體盤、調隙裝置、輸出軸等組成。輸入端通過軸套與驅動電機相連，軸套固定在導體軛鐵上，導體軛鐵既可以固定銅盤作用又可以引導永磁體產生的磁力線，使更多磁力線進入銅盤，提高傳遞效率，銅盤通過內六角螺栓固定在導體軛鐵上，永磁體嵌鑲在鋁制的永磁體盤內，防止永磁體間漏磁，鋁盤固定在永磁軛鐵上。永磁體、鋁盤和法蘭盤組成永磁體盤，2個永磁體盤通過調隙裝置連接，呈對稱布置。銅盤和永磁體間的距離相等，永磁轉子盤固定在輸出軸上，如圖1所示。

當銅盤隨輸入軸一起旋轉時，銅盤與永磁體盤之間形成轉差，根據法拉第電磁感應定律，磁通量通過銅盤以一定規律發生變化，交變磁場在銅盤上產生渦流，渦流產生的感應磁場與永磁體磁場之間共同作用下產生力矩，并在銅盤表面產生熱量。產生的力矩驅動永磁體盤隨著銅盤做同向旋轉，帶動輸出軸轉動，從而將動力傳遞至負載。

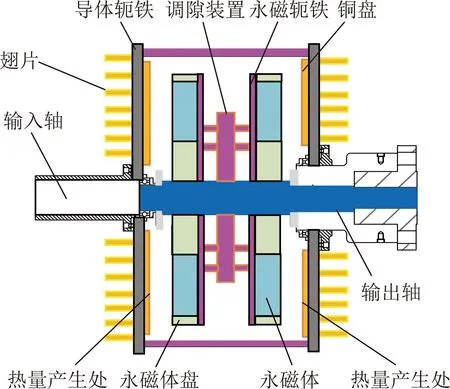
圖1 雙盤式磁力耦合器模型Fig.1 Double disk magnetic couple model

1.2 模型原理

如圖2所示，建立的模型包括熱源、銅盤、導體軛鐵以及散熱翅片。銅盤連接熱量產生處，導體軛鐵連接翅片，可使銅盤上產生的熱量均勻的依次傳遞至導體軛鐵、翅片，最終利用翅片表面與環境的熱交換帶走熱，避免銅盤表面堆積大量熱量。除此之外，各個連接處均采用導熱膠填補，達到減少各元件之間接觸熱阻的目的[18]。由于雙盤式磁力耦合器左右兩側具有對稱性，為了簡化計算量，故只分析左側傳熱模型。

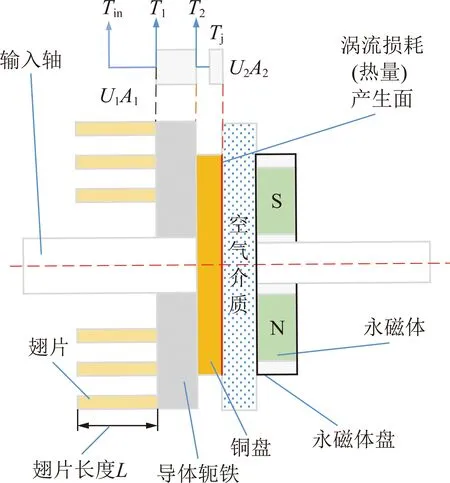
圖2 雙盤式磁力耦合器傳熱模型Fig.2 Heat transfer model of double disk magnetic coupler

圖2中，Tin，T1，T2和Tj分別為背景溫度、冷端溫度、熱端溫度、渦流溫度；U2A2和U1A1為熱端、冷端的傳熱性能[19-20];U2為熱端電壓;A2為熱端面積;U1為冷端電壓;A1為冷端面積。

1.3 熱力學分析

與導體軛鐵的電阻相比，聯接處的接觸電阻很小，可忽略。故在建立熱平衡方程時，忽略接觸熱阻，傳熱模型的熱平衡方程如下：

q1=ST1r-0.5r2R-K(T2-T1)

(1)

q2=ST2r+0.5r2R-K(T2-T1)

(2)

其中，q1為散熱量，W；q2為銅導體盤上產生的熱量，W；S為傳熱模型的總塞貝克系數；r為輸入電機的轉速，r/min；R為傳熱模型的電阻；K為總熱導，W/K；S，K，R均為重要的物性參數。對該模型進行傳熱過程推導，可得散熱量與溫差的計算公式為

(3)

(4)

式中，η為等效效率；i為銅導體盤上產生的電流。

散熱量還可用式(5)表示：

q1=(Tj-T1)U1A1

(5)

聯合式(1)～(5)，推導出冷熱兩端的溫度數學式。根據電磁感應原理，銅導體表面渦流溫度Tj以及導體軛鐵上翅片所處的背景溫度Tin，可根據式(6)和(7)依次得出溫度T1和T2，即

(6)

(7)

為分析該過程的熵產大小，則熵產Sg為

(8)

2 基于Ansoft-3D仿真的數據獲取

Ansoft-3D獲取目標變量對應的散熱量與熵產的操作主要包括3步：前處理、模擬過程、后處理[21]。前處理主要考慮：三維模型、Maxwell模型、熱傳導模型、網格劃分、傅里葉定律、設計參數的選擇。前處理的參數經過Ansoft-3D仿真的求解器轉換得到渦流溫度。散熱量和熵產可由渦流熱量經過相應的公式轉化得到，圖3為仿真流程。

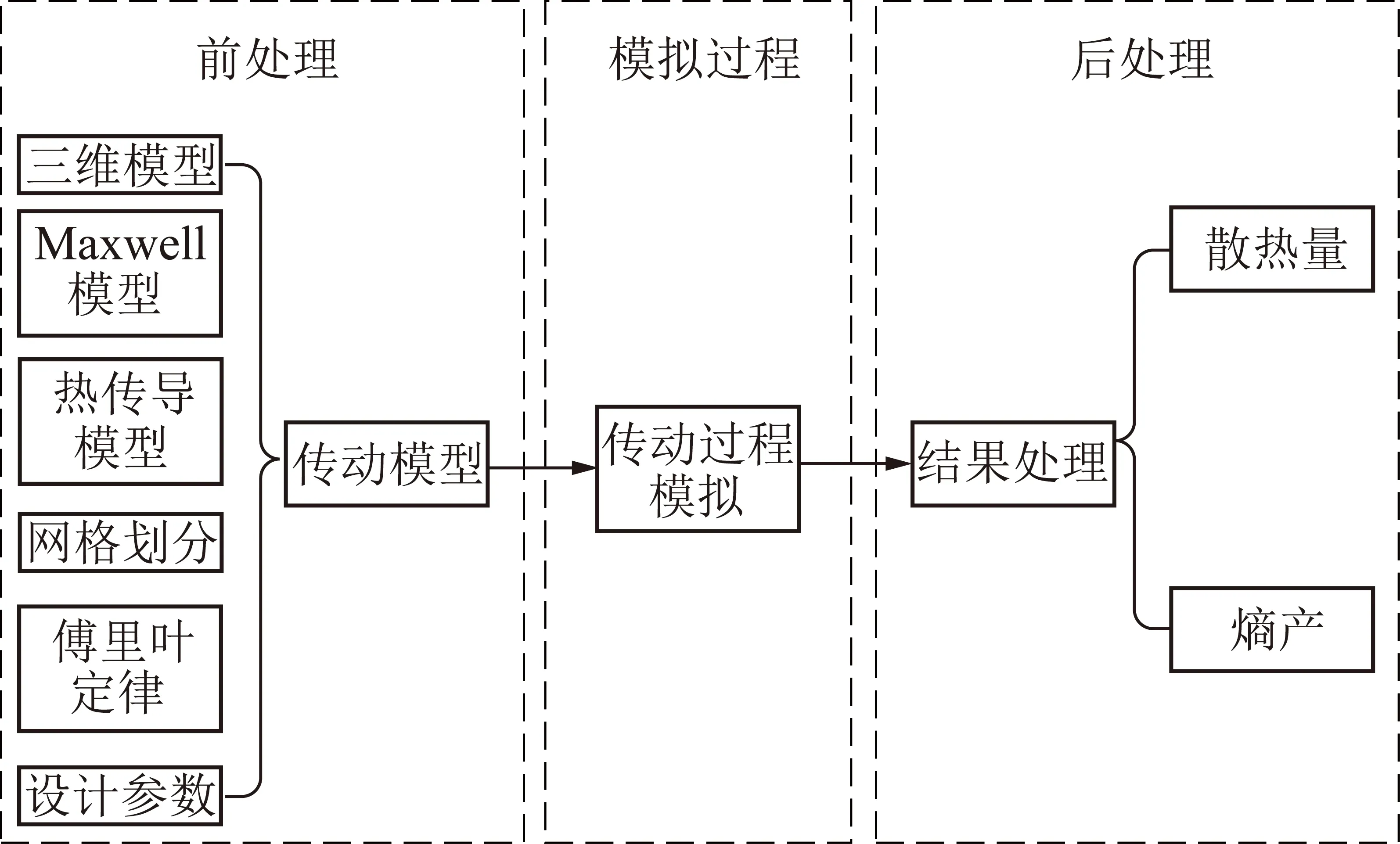
圖3 仿真流程Fig.3 Simulation flow chart

2.1 Ansoft-3D前處理的關鍵技術

采用Solidworks軟件完成雙盤式磁力耦合器永磁體盤、銅導體盤的三維模型建立，以.x_t形式導入Ansoft-3D軟件中，如圖4所示。

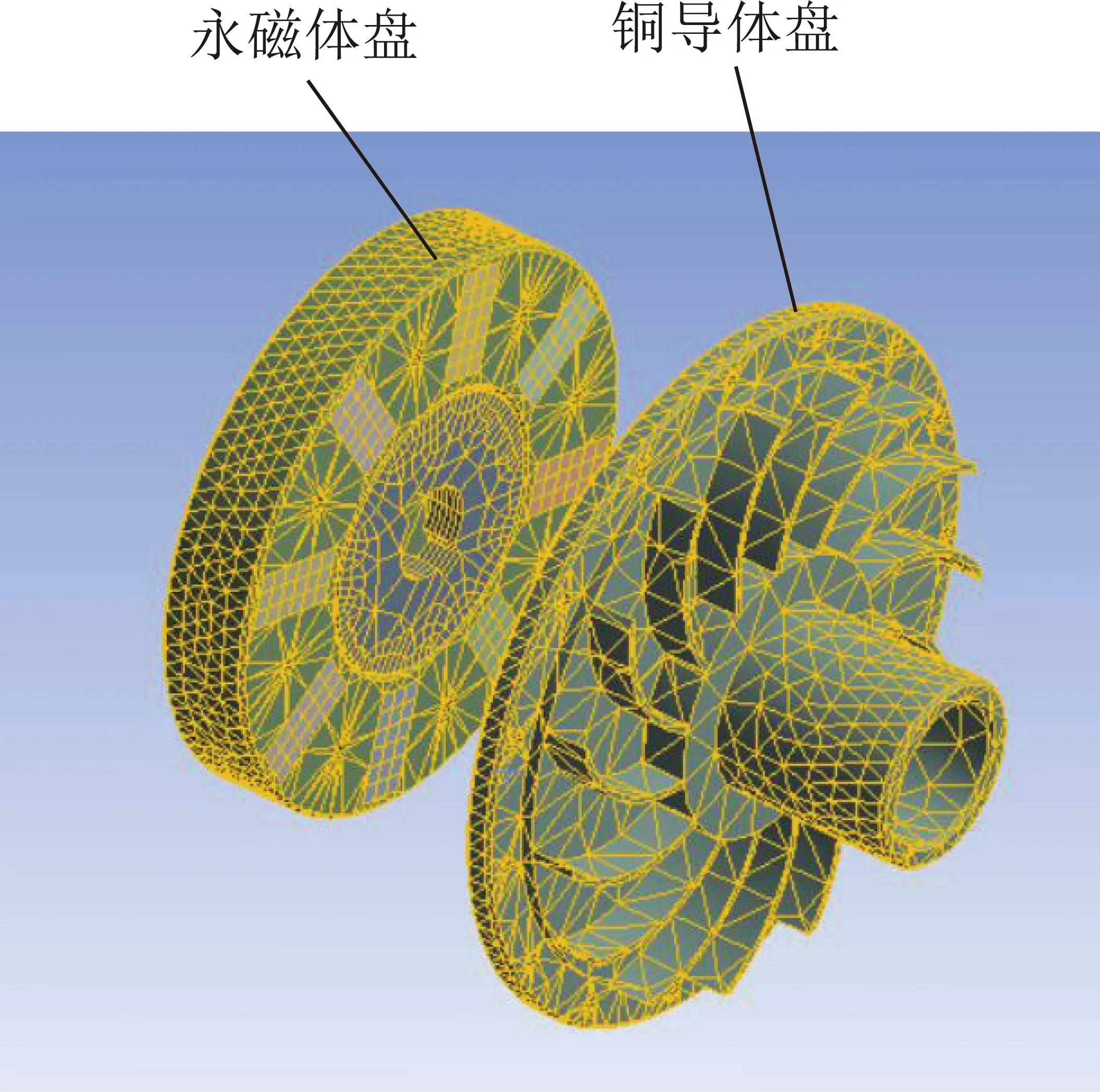
圖4 網格劃分Fig.4 Grid division

參數項的設置會造成仿真結果與實際結果的誤差，其中永磁體盤和銅導體盤網格數目根據仿真調試得出，其他模型與參數根據相應的文獻參考選擇[22]。將雙盤式磁力耦合器傳動過程中可控因素的輸入電機的轉速nin、翅片個數N，翅片長度L，永磁體盤與銅盤之間的氣隙長度Lg作為仿真的輸入，探索輸入與散熱量、熵產2個目標之間的關系，為此設計了四因素五水平的正交試驗來進行仿真分析，各參數的取值見表1。

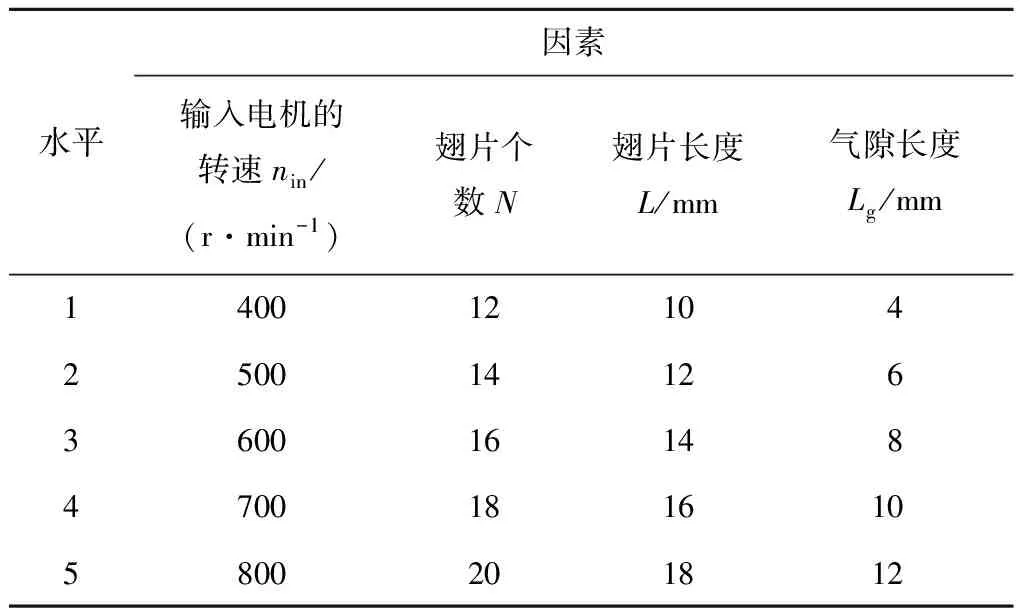
表1 正交試驗切削參數

2.2 單參數分析

對單參數進行分析，以確定輸入電機轉速、氣隙長度、翅片個數、翅片長度等參數對散熱量和熵產的影響。參考煤礦井下工作溫度，設置環境溫度為22 ℃，圖5(a)為輸入電機轉速與散熱量的關系，圖5(b)輸入電機轉速與熵產的關系。可以看出散熱量隨著輸入電機轉速先增加后減少，這是因為式(1)中其他參數為定值時，散熱量q1關于輸入電機轉速r呈二次拋物線關系。由式(8)可知，Tin和Tj固定時，熵產只與q1，q2之差有關，故熵產隨著輸入電機轉速單調增加。

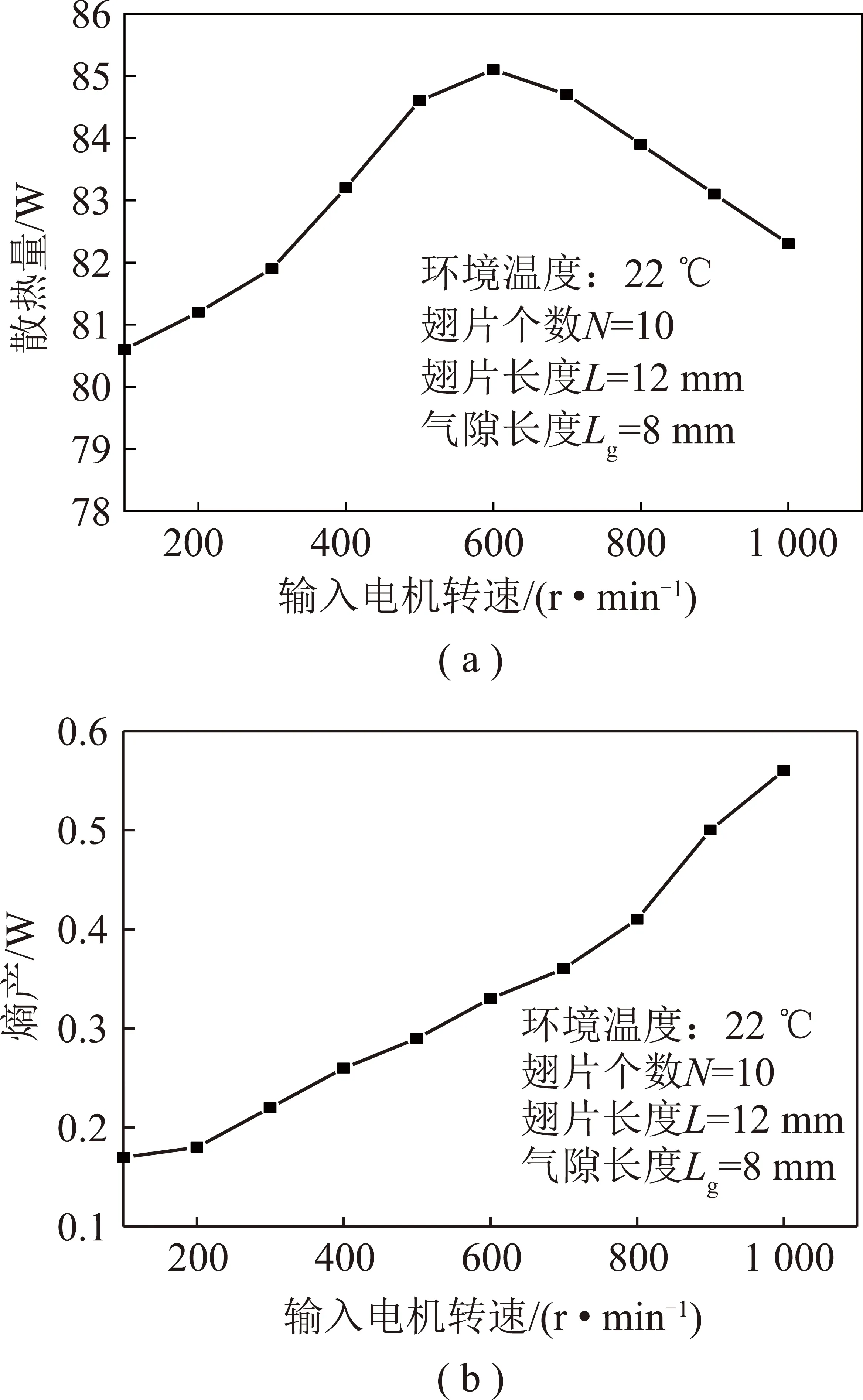
圖5 散熱量、熵產和輸入電機轉速關系Fig.5 Relations among heat dissipation，entropy generation and input motor speed

塞貝克系數S與翅片個數N呈線性關系[16]，結合式(1)，當其他參數固定時，散熱量q1與S也呈線性關系，故如圖6(a)所示，散熱量隨著翅片個數單調增加。圖6(b)中，當Tin和Tj固定時，熵產依然只與q1，q2之差有關，故熵產隨著輸入電機轉速單調增加。熵產仍隨著翅片個數的增加而增大。

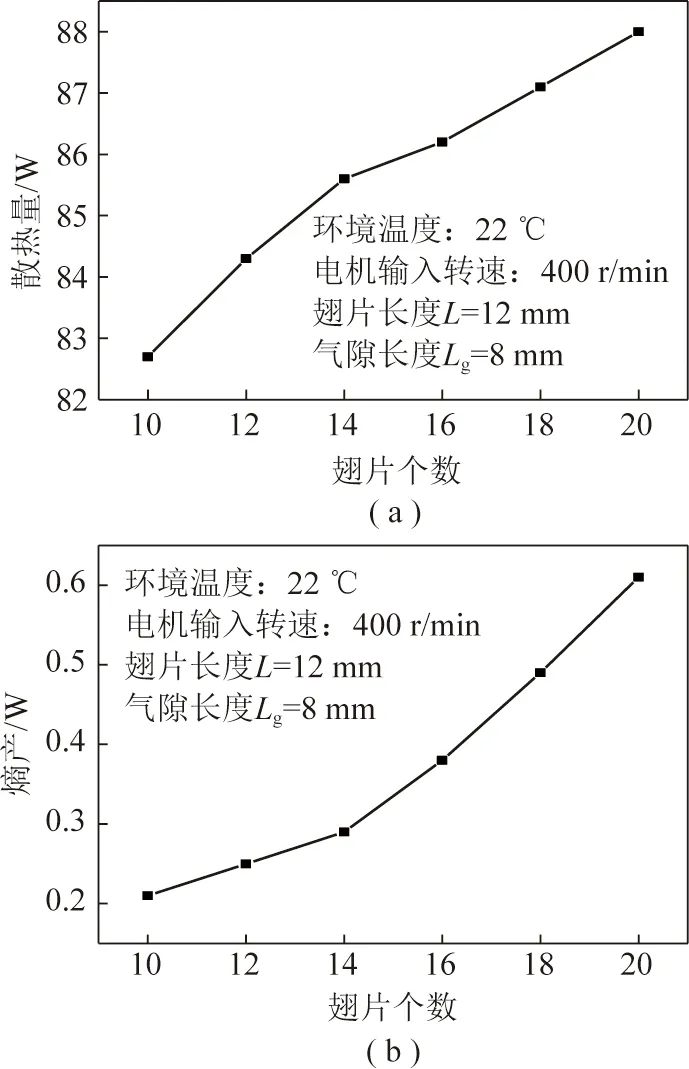
圖6 散熱量、熵產和翅片個數關系Fig.6 Relations among heat dissipation， entropy production and number of fins

如圖7(a)所示，翅片長度直接影響熱導K及電阻R大小，散熱量q1隨翅片長度增大而增大，但是當翅片長度達到14 mm后，散熱量增加不明顯。當環境溫度較小時，熵產隨著翅片長度變化不明顯，因而整體較為平穩，如圖7(b)所示。

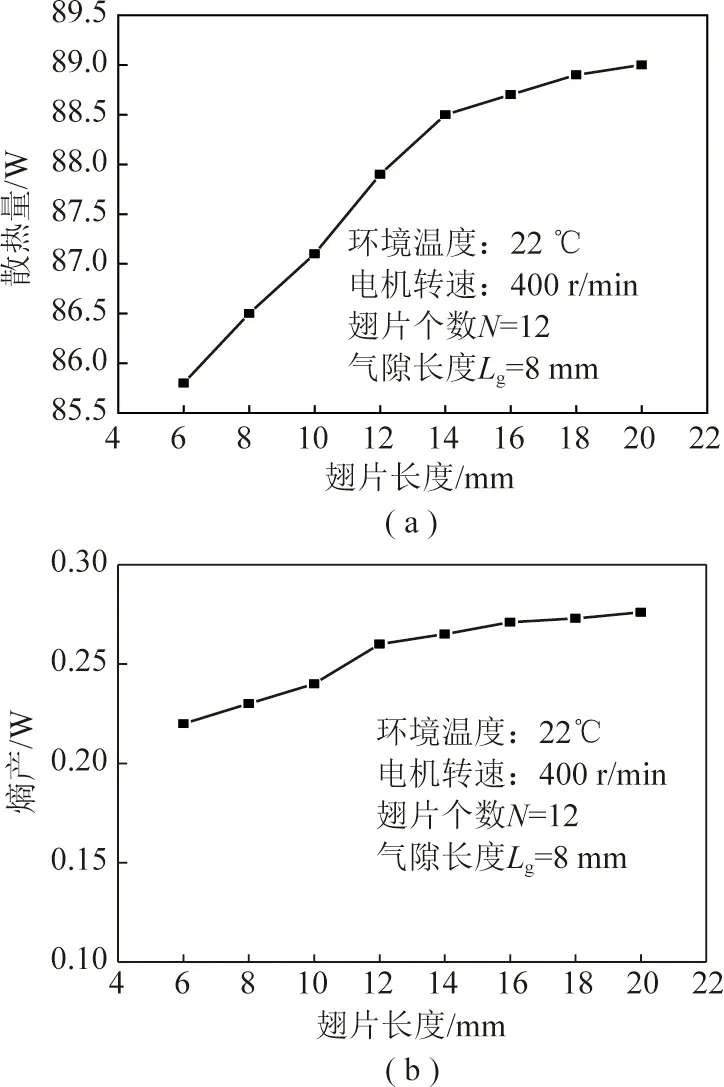
圖7 散熱量、熵產和翅片長度關系Fig.7 Relations among heat dissipation，entropy production and length of fins

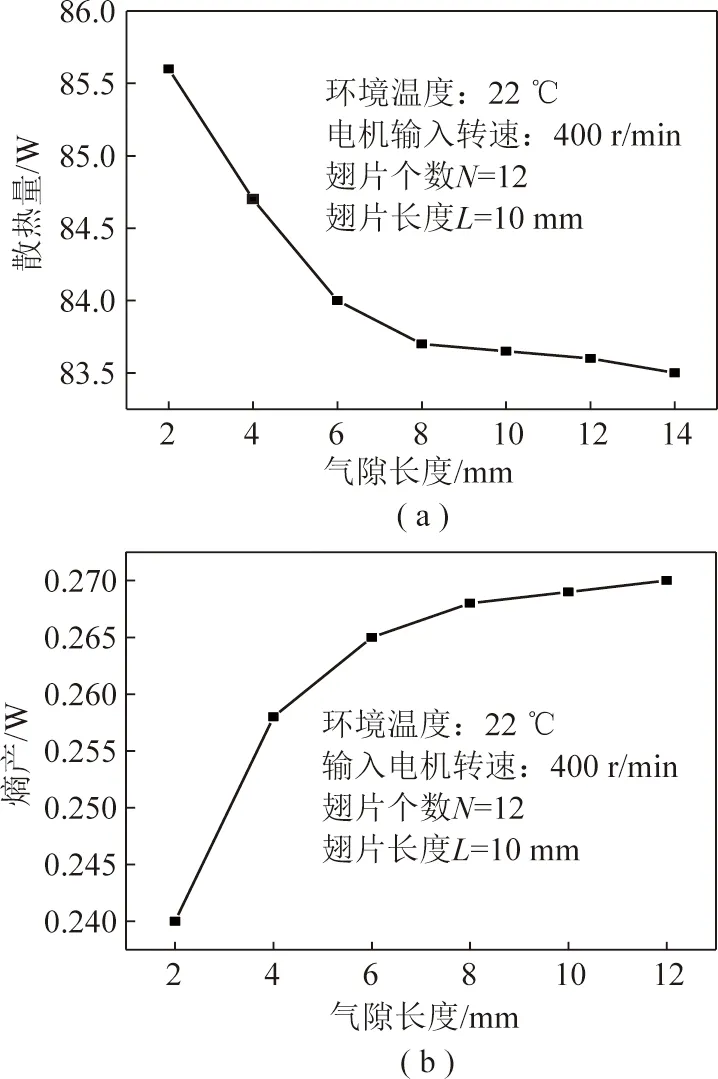
圖8 散熱量、熵產和氣隙長度關系Fig.8 Relations among heat dissipation， entropy production and air gap length

當氣隙長度增大時，造成氣隙的等效磁阻增大[13]。散熱量隨著氣隙長度增大而減小，這與式(1)符合。但是當氣隙長度增加至8 mm后，散熱量的變化量逐漸減小，趨近于水平線，如圖8(a)所示。熵產隨著氣隙長度增大而增大，一旦增大至8 mm以后，熵產增加量不明顯，如圖8(b)所示。

選取環境溫度為22 ℃，氣隙長度為6 mm，輸入電機轉速為400 r/min，翅片長度依次為10，12，14，16 mm的渦流密度云圖如圖9所示。由圖9可知，當翅片長度逐漸增加時，模型的最低溫度在翅片外端，渦流密度最低值依次為3 300，2 752，928.64，648.82 W/m2。這與理論計算式(1)，(2)相吻合：翅片越長，與空氣接觸的散熱面積增加，使電阻R越小，則散熱量增加，而傳動過程中產生的渦流熱量降低。

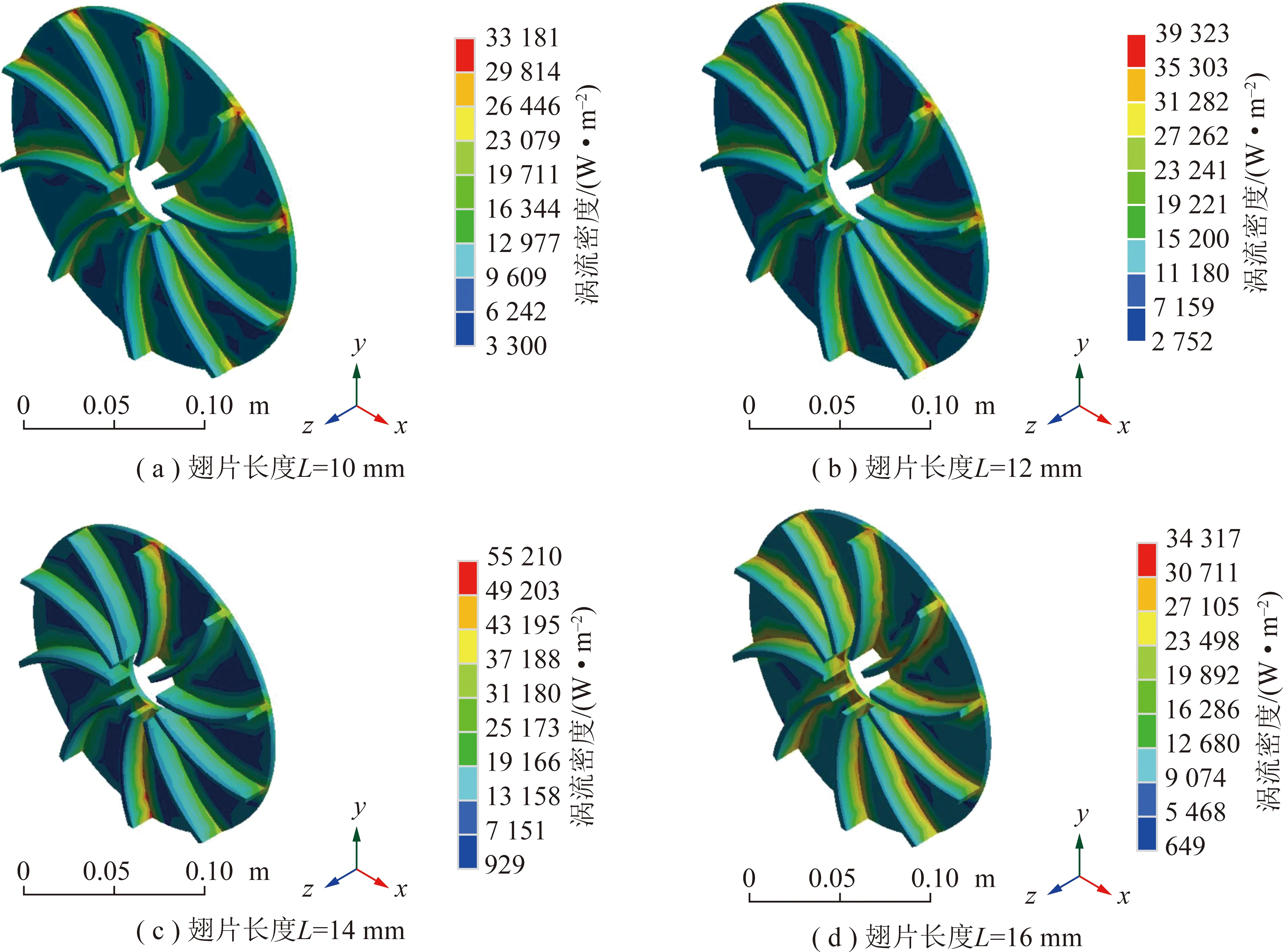
圖9 仿真云圖Fig.9 Simulation diagram

3 物理試驗的驗證

3.1 物理平臺的搭建

為了驗證上述理論分析與有限元仿真的結果，選取與仿真相同的參數在雙盤式磁力耦合器上進行永磁渦流傳動試驗，現場試驗平臺如圖10所示。

圖10 試驗平臺Fig.10 Test platform

三相異步電機采用380 V三相低速電動機。通過變頻器控制電動機，本實驗臺額定功率為55 kW，最大轉速為3 000 r/min，建議轉速為0～2 000 r/min。測量回路配置NCTES3000轉矩轉速測量儀(測試精度：0.2%，量程：500 N· m)、MIK-2740溫度巡檢儀連接計算機完成信號采集和測量任務。采用西門子S7-200系列PLC進行連鎖控制。

3.2 物理試驗與有限元對比

對25組仿真與物理試驗的數據進行正交試驗。有限元仿真后在銅導體表面上選取3個不同位置采集渦流溫度，最終以這3處渦流溫度的平均值作為最終的渦流溫度。而物理實驗的渦流溫度通過溫度傳感器2測量得到，將仿真和物理實驗的渦流溫度代入式(5)即可算出散熱量q，代入式(1)，(2)，(8)可算出熵產Sg。正交試驗方案和結果見表2，其中，因素A為輸入電機的轉速nin，r/min；B為翅片個數N；C為翅片長度L，mm；D為氣隙長度Lg，mm。

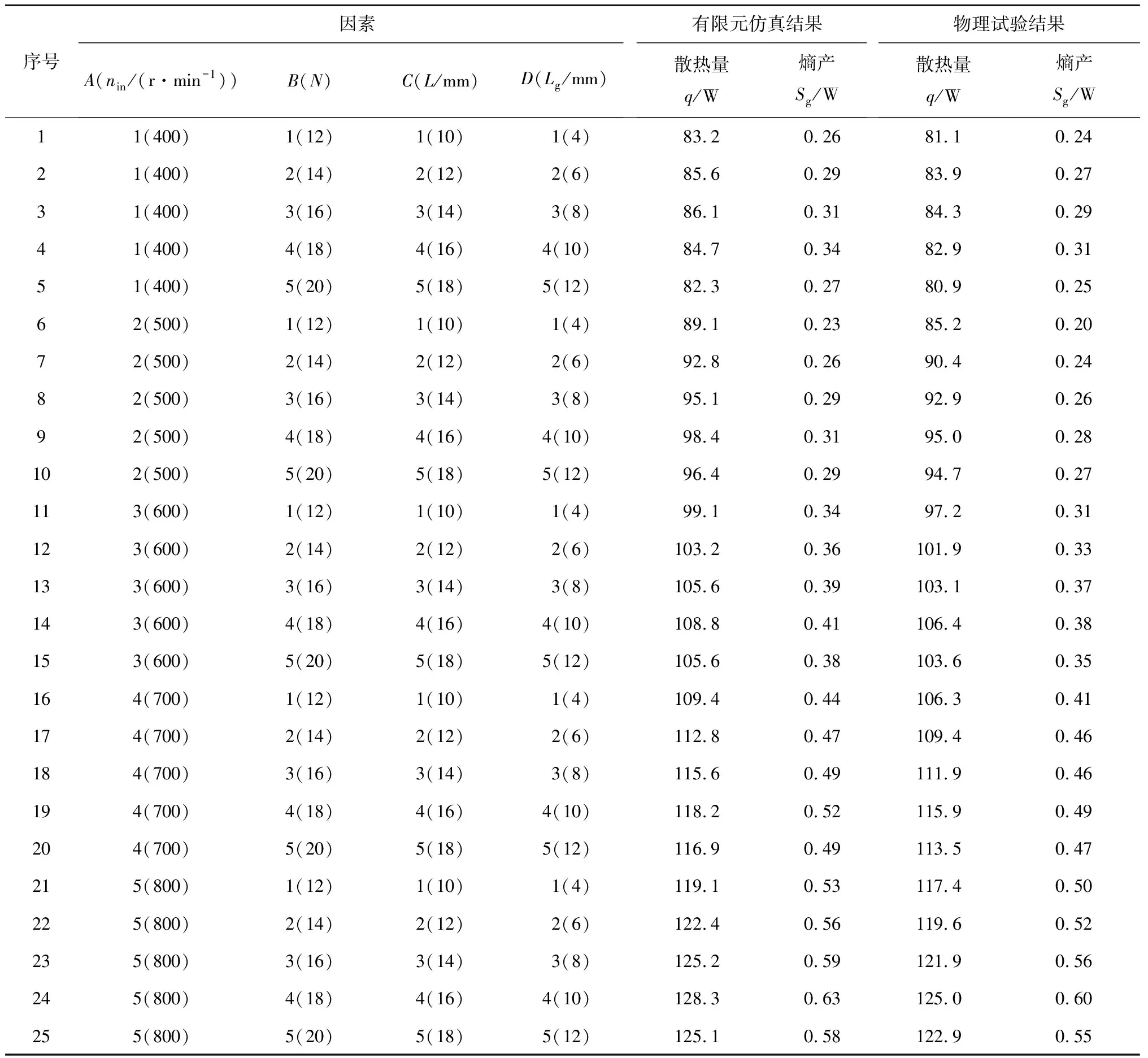
表2 正交試驗設計方案以及仿真和物理試驗結果

由圖11可知，有限元仿真數據與物理實驗數據具有相同的變化趨勢，散熱量與熵產誤差的均值為4.6%和9.2%，基本驗證了熱力學模型和有限元分析的準確性。

4 考慮多物理場耦合與熵產分析的多目標優化算法的構建

高斯過程回歸方法(GPR)在解決高維度輸入、小樣本空間與非線性問題上具有良好的性能，適宜作為處理第3節中正交試驗數據的方法。采用人工蜂群算法改進的高斯過程回歸模型作為有限元仿真的代理模型，該模型選擇適用于非線性關系的平方指數協方差和線性協方差相結合的組合協方差函數[23]。基于Pareto分配關系，利用多目標粒子群優化算法，以散熱量和熵產為目標優化參數，其流程圖如圖12所示。

需要優化的耦合能量和熵產之間存在著相互制約的關系。基于Pareto分配關系，改進人工蜂群算法構建高斯過程回歸模型，采用多目標粒子群算法來解決兩者之間的優化平衡問題。以永磁傳動四要素為決策變量，以散熱量和熵產作為優化目標，其優化問題可以表示為

(9)

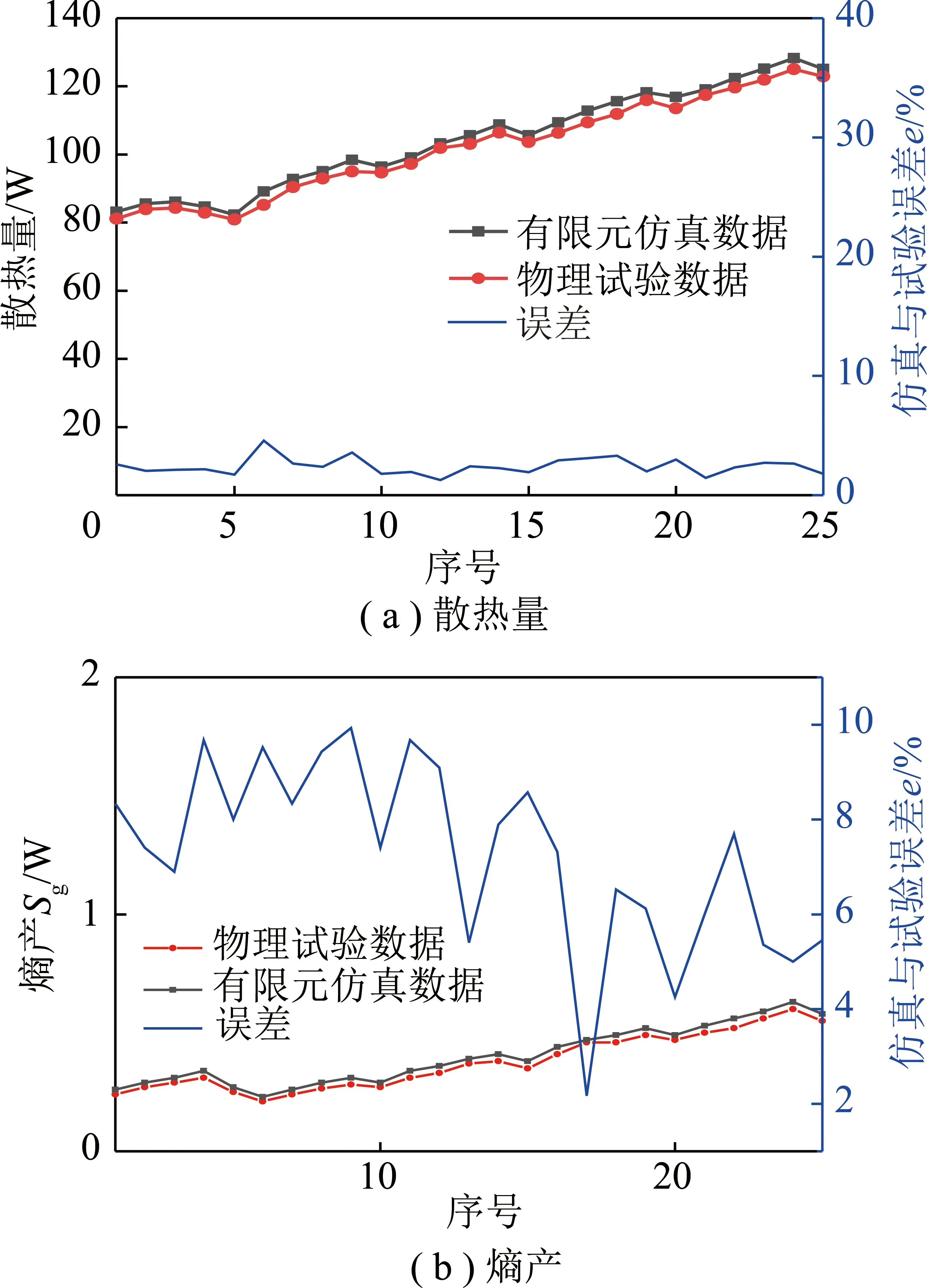
圖11 物理試驗數據與仿真數據的對比Fig.11 Comparison of physical test data and simulation data

該算法優化流程的具體步驟如下：

(1)初始化多目標粒子群的基本參數，見表3。在式(9)中給出的決策變量范圍和最大最小粒子速度范圍內初始化各粒子的速度xj和對應的速度vj，其中j∈[1,K]表示種群數；將改進人工蜂群算法構建的高斯 過程回歸模型預測散熱量和熵產的函數作為適應度函數，依據Pareto分配原則計算得到存放非劣解的archive集。

表3 優化基本參數設置

(2)根據粒子的適應度確定個體的最優解，然而當個體的最優解不能確定時，隨機選取一個解作為個體歷史最優，記為pbest；根據適應度范圍和網格擴展因子確定網格范圍并隨之劃分網格。計算archive集在網格中的擁擠度，并選擇當前全體中擁擠度小的位置(種群最優解)記為gbest。

(3)更新archive集中粒子的速度、位置，以求解出粒子當前迭代過程中最好的pbest，表達式為

(10)

(11)

式中，k為當前迭代次數；C0為權重衰減因子；w為慣性權重，w(k+1)=C0w(k);c1，c2分別為個體與種群學習因子；r1，r2為0～1的隨機數。

(4)通過比較當前迭代過程中全部粒子的適應度，將非支配解存儲入archive集中，由此對archive集進行維護和更換。

(5)當算法迭代的次數達到預設的次數時程序就會停止，與此同時存儲在外部檔案中的所有解集就是Pareto前沿；若未達到條件要求則會返回步驟(1)。

5 結果對比與分析

5.1 改進人工蜂群算法-高斯過程回歸模型的預測效果

將有限元仿真得到的25組數據作為改進人工蜂群算法-高斯過程回歸模型的數據集，選取20組數據作為該模型的輸入，其中15組為訓練樣本，5組為尋優樣本，剩余5組為與預測值對比的樣本。改進人工蜂群算法-高斯過程回歸模型的散熱量與熵產預測結果如表4和圖13所示。仿真值與預測值吻合較好，且平均誤差百分比(EMAP)依次為2.49%和7.80%，均小于10%,基本驗證了該模型的有效性。

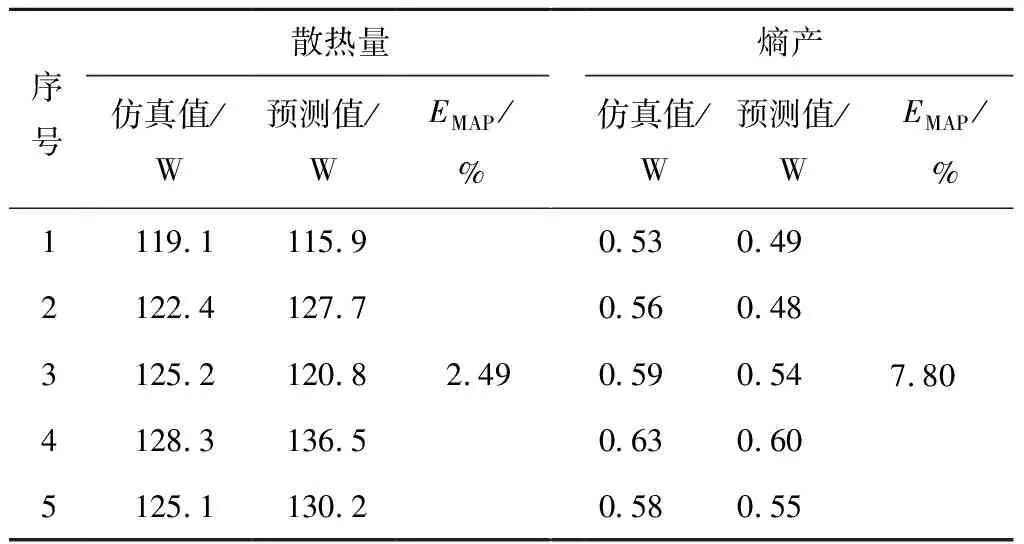
表4 預測值與仿真值對比

圖13 預測值與仿真值對比Fig.13 Comparison between predicted value and simulation value

為對比改進人工蜂群算法-高斯過程回歸模型的性能，本文采用天牛須搜索算法[24](Beetle Antennae Search algorithm，BAS)、粒子群優化(PSO)算法[25]分別優化高斯過程回歸模型，構建天牛須搜索算法-高斯過程回歸模型(BAS-GPR)和粒子群優化算法-高斯過程回歸模型(PSO-GPR)。在以上3種模型下將預測散熱量和熵產的效果進行了對比，并且采用模型精度的評價指標：均方誤差(EMS)、EMAP、決定系數(R2)、對稱平均百分比誤差(ESMAP)和模型復雜度評判指標(運行時間T)來比較。其中，均方誤差(EMS)、決定系數(R2)、對稱平均百分比誤差(ESMAP)的公式如下:

(12)

(13)

(14)

式中，ESS為殘余均方根誤差；TSS為方差總和。

3種優化算法依據EMAP、式(12)～(14)計算出各指標見表5。為了方便對比，將散熱量和熵產預測效果較優的結果用下劃線表示。綜合看來，本文所提出的改進人工蜂群算法-高斯過程回歸模型(ABC-GPR)的效果最優。而基于圖13的預測趨勢和均方誤差(EMS)、EMAP、對稱平均百分比誤差(ESMAP)這些反映偏差的指標來說，預測趨勢符合仿真模擬趨勢。預測值和仿真值的平均偏差較小，2個表示百分比的指標(EMAP和ESMAP)均小于10%，因此可以認為利用改進人工蜂群算法-高斯過程回歸模型(ABC-GPR)預測散熱量和熵產具有可行性。

5.2 多目標優化結果及其驗證

運行改進人工蜂群算法構建的高斯過程回歸模型(ABC-GPR)，采用多目標粒子群算法來解決散熱量與熵產兩者之間的優化平衡問題，算法運行結果如圖14所示。其中黑色點不被其他點支配(Pareto前沿)，藍色點完全被其他點支配，紅色點為個體最優解所對應的目標值。各設計參數下Pareto前沿以及目標值見表6。在其中選擇一組優化后的參數{nin，N，L，Lg}={758 r/min，16，14.8 mm，6.6 mm}，其對應的散熱量和熵產依次為：128.2 W，0.41 W。將該組參數進行物理實驗，以驗證該優化算法的有效性。

基于以上搭建的雙盤式磁力耦合器實驗平臺，按照優化后的設計參數設置，通過試驗可得到對應的散熱量和熵產。為了避免偶然性，對該組數據重復進行

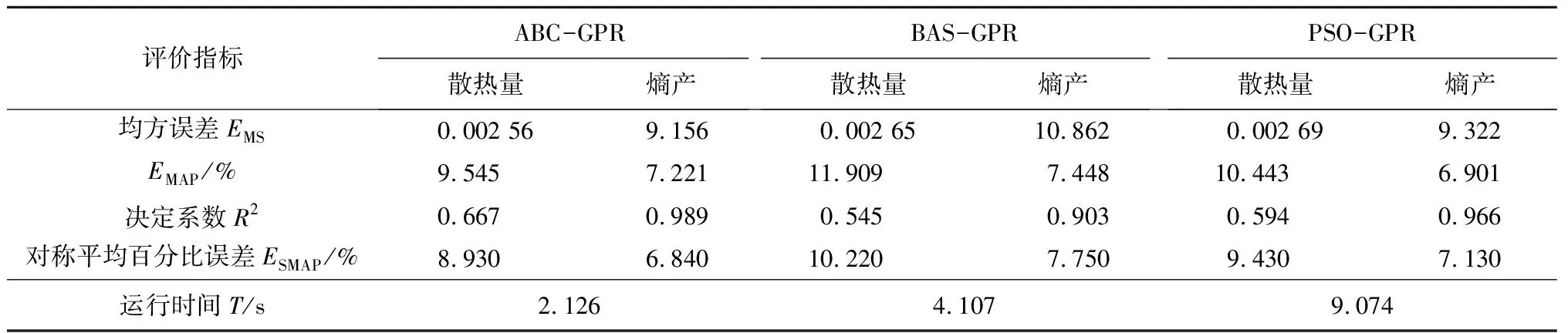
表5 3種優化算法各指標下的結果

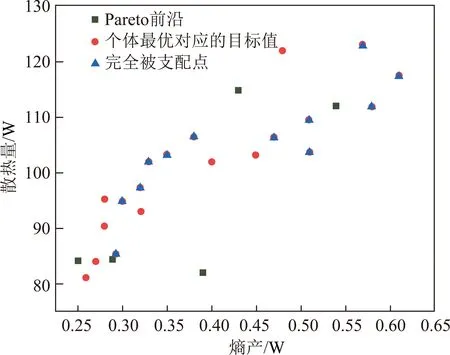
圖14 優化算法的Pareto解(黑色點方形點)Fig.14 Pareto solution of optimization algorithm (black dot and square dot)

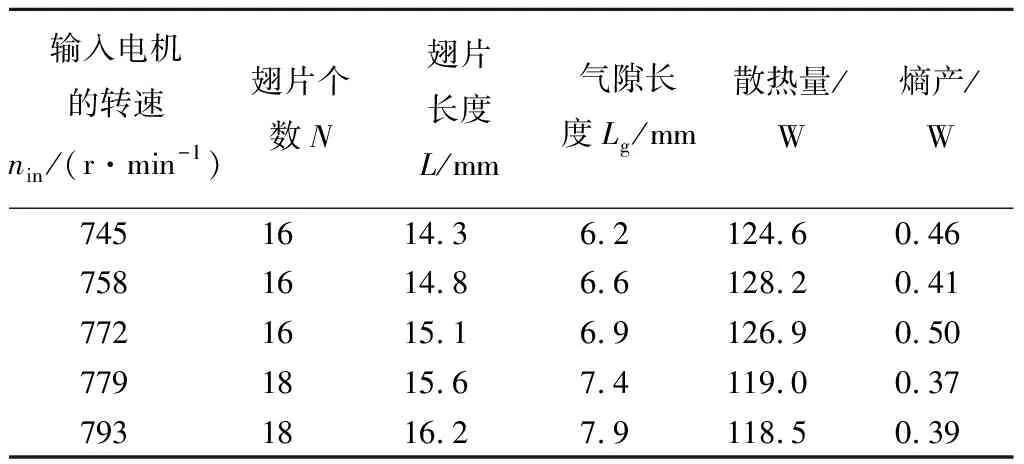
表6 多目標優化結果

5次試驗，得到的結果見表7。根據計算結果，散熱量和熵產與相應優化結果的平均誤差依次為5.614%，8.192%，該組優化后的參數滿足實際傳動期望達到的效果，可用于指導煤礦永磁渦流傳動系統的設計。

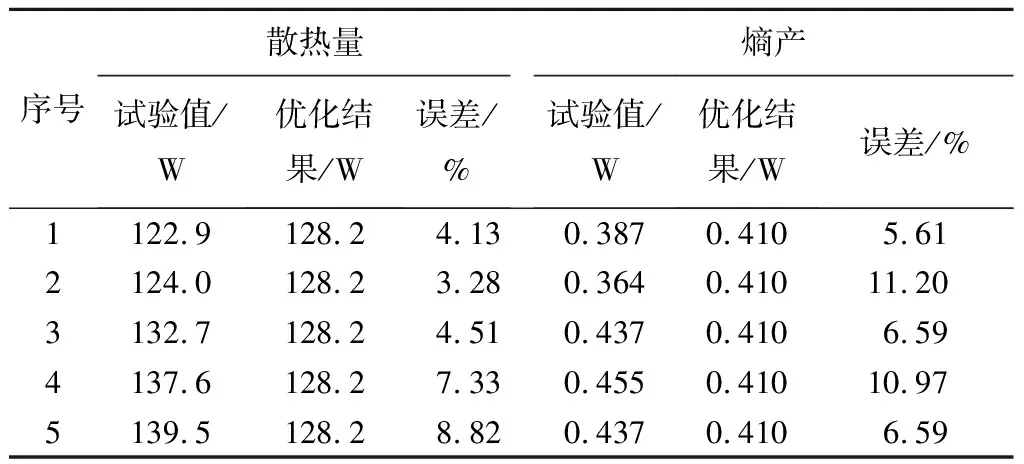
表7 試驗值

6 結 論

(1)基于能量平衡和熵產最小化理論，通過效率單元法和穩態熱傳遞，建立了礦用雙盤式磁力耦合器的熱力學數學模型。利用有限元法仿真得到不同參數下的散熱量與熵產，與對應的物理實驗測量值具有相似的變化趨勢，并且散熱量與熵產的誤差均值分別為4.6%和9.2%，基本驗證了熱力學模型和有限元分析的準確性。

(2)采用改進的人工蜂群算法(ABC)優化的高斯回歸模型(GPR)對散熱量和熵產的預測中，ABC算法預測的精度高于已有文獻中的天牛須搜索算法(BAS)和粒子群算法(PSO)的預測精度，并且響應時間耗時也最少，僅為2.216 s。

(3)在ABC-GPR模型產生的參數與散熱量和熵產之間的映射關系的基礎上，利用多目標粒子群優化算法，得到了散熱量和熵產的Pareto前沿。并采用物理試驗驗證了該結果的正確性，證明了該算法的可行性，有助于提高雙盤式磁力耦合器的傳動效率。