讓抽象的符號承載起數學思維的綻放

池紅梅

［摘 要］符號意識是指能主動地去感知和理解符號，積極運用各類符號來幫助自己理解、表達、分析和解決問題，并且讓這樣一種能力內化為骨子里的意識。每一個數學符號都是人類智慧的結晶。讓學生經歷數學符號的再創造過程，讓抽象的符號承載起意義的理解、規律的表達、文化的浸潤，是培養學生符號意識的有效途徑。

［關鍵詞］符號意識；意義理解；規律表達；文化浸潤

［中圖分類號］ G623.5 ［文獻標識碼］ A ［文章編號］ 1007-9068（2022）26-0004-04

數學符號具有準確性、抽象性、形式化等特征。常見的數學符號從作用上可分為元素符號、關系符號、運算符號、結合符號、性質符號、標識符號和單位符號七大類，每一個數學符號都經歷了“萌芽創生—使用優化—推廣應用”的發展過程。從某種程度上來講，數學學習過程便是和數學符號打交道的過程。數學符號本身所具備的簡潔性、代表性、準確性使其具有極大的推廣性與實用性，但數學符號的高度抽象性與形式化的特征，也給學生的學習帶來了困難。因此，只有讓抽象的符號承載起數學思維的綻放，方能達到課程標準對學生符號意識的培養要求。

一、符號意識的內涵解讀

符號，指代表事物的標記、記號，從廣義上來看，聲音、語言、文字、動作、圖表、圖畫、圖像等均屬于符號的范疇。意識，即為覺察，如看見樹枝發綠就意識到已經是春天了；又指人的頭腦對客觀物質世界的反映，是感覺、思維等各種心理過程的總和，其中的思維是人類特有的反映現實的高級形式。《義務教育數學課程標準（2011年版）》將符號意識解讀為“符號意識主要是指能夠理解并且運用符號表示數、數量關系和變化規律；知道使用符號可以進行運算和推理，得到的結論具有一般性”。建立符號意識有助于學生理解符號的使用是數學表達和進行數學思考的重要形式。由此可見，符號是一種靜態的存在，記住符號本身并不是最重要的，最重要的是能主動地去感知和理解符號，積極運用各類符號來幫助理解、表達、分析和解決問題，并且讓這樣一種能力內化為骨子里的意識：不需要任何外界的提示，大腦便會主動運用符號去進行思維，就如人的潛意識一般。

生理學上有一個現象叫“肌肉記憶”，即人體的肌肉是具有記憶效應的，同一種動作重復多次之后，肌肉就會形成條件反射。由此說明，加強訓練，不僅大腦，連肌肉也能形成記憶。當然，培養學生的符號意識并不是說要進行大量、機械的重復練習，相反，符號意識的形成并非一日之功，唯有持之以恒。

二、培養符號意識的教學實踐

對于北師大版教材四年級上冊第五單元“認識方程”中的“用字母表示數”，很多教師都認為這是培養學生符號意識的第一節課。其實不然，學生從學前教育開始，甚至從呱呱墜地開始，就已無意識地接受各種與數學符號有關的教育。因此，教師要從一年級開始強化學生符號意識的培養。

1.讓符號承載起意義的理解

【案例1】從計數到記數，完成對抽象數字符號的意義建構

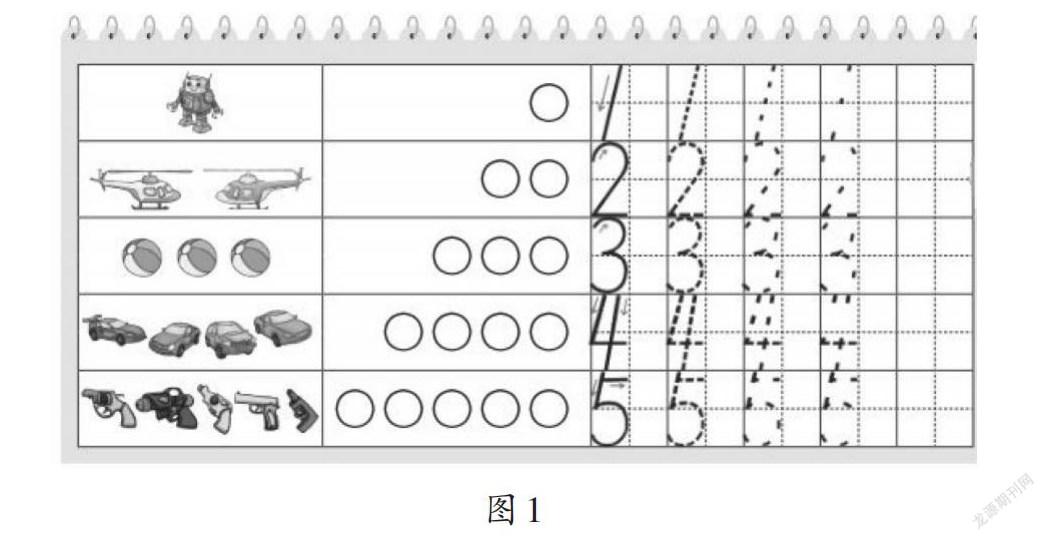
計數，即把數量數出來；記數，即把數出來的數表示出來。現在使用的阿拉伯數字0～9，便是將數出來的數表示出來，其數字符號本身并不具備相應的數量意義。比如數字3，和它所表示的數量3是沒有任何關系的。在人類的記數發展中，先是采用刻痕、結繩等方式進行一一對應的實物記數，再用小棒、圓圈等進行半抽象記數，最后發展到用全抽象的符號記數。以教材圖（如圖1）為例，對于3個皮球，先是畫3個圓圈表示，感受到自然數一個一個累加的屬性，再約定俗成：凡是像這樣具有3個屬性的物體，都用符號“3”來表示，其他數字符號也是如此。也就是說，如果一開始，用符號“4”來記錄數量3，那現在的數字3就是數字4的模樣。抽象的數字符號，是人類在歷史長河中通過優化而流傳下來的約定俗成。

在教學這部分內容時，教師需要帶領學生先深度理解一一對應的計數，再過渡到抽象的記數，最后形成符號意識：3個蘋果、3筐蘋果、3棵蘋果樹、3頭牛、3座房子……不管物體的形狀、大小、屬性如何，均可以用符號“3”來表示，也就是它們的數量都是3。

【案例2】從數位到數值，完成對位值制的意義建構

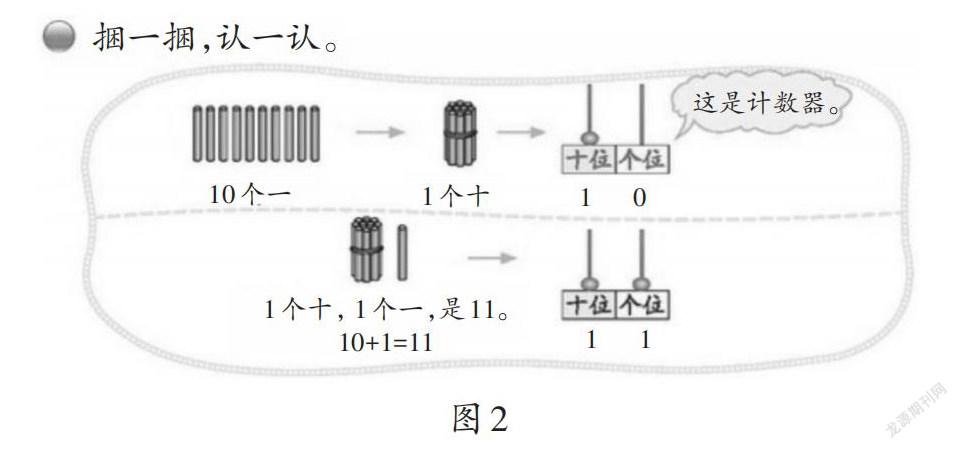
學生經歷了對0～9的數字符號的意義建構后，學習數字符號10，11……是一個記數意義的重要跨越，即位值制。北師大版教材一年級上冊第七單元“加與減（二）”的第一課時為“古人計數”，教學內容為讓學生認、讀、寫11～20各數。對此，部分教師理解不夠，認為學生早就會認、讀、寫100以內的數，不明白為什么還要專門安排課時來學習。本課教學的核心目標是讓學生認識到位值制的意義，像符號“10”，明明就是一個數字符號“1”和一個數字符號“0”的組合，怎么就能表示數量10的意義呢？同樣的，11明明就是兩個數字符號“1”的組合，怎么就能表示數量11的意義呢？

“古人計數”（如圖2）這一課是學生第一次正式學習個位、十位，也就是數位的相關知識。按照0～9的抽象記數法則，是不是每一個不同的數都要創造一個與之對應的抽象的數字符號呢？數的個數是無限多的，要創造無限多個數字符號來表示不同的數，只會極大地加重人類的記數與運算等負擔，于是隨著社會的發展，人類最終選擇用位值制來作為通用的記數法則。本課的教學重點便是讓學生認識到，不同的數字符號在不同的位置可以表示不同的意義及大小。“抽象的數字符號+不同的位置”是學生后續學習更大的數與更小的數（小數）的意義的根基。比如，在教學小數的意義時，為什么小數點的移動會改變小數的大小？其根本原因是小數點所處的位置不同，各個數字所在的數位便不同，其表示的大小與意義自然也就不同。

2.讓符號承載起規律的表達

【案例3】“一下打一串”，促進代數思維的萌芽

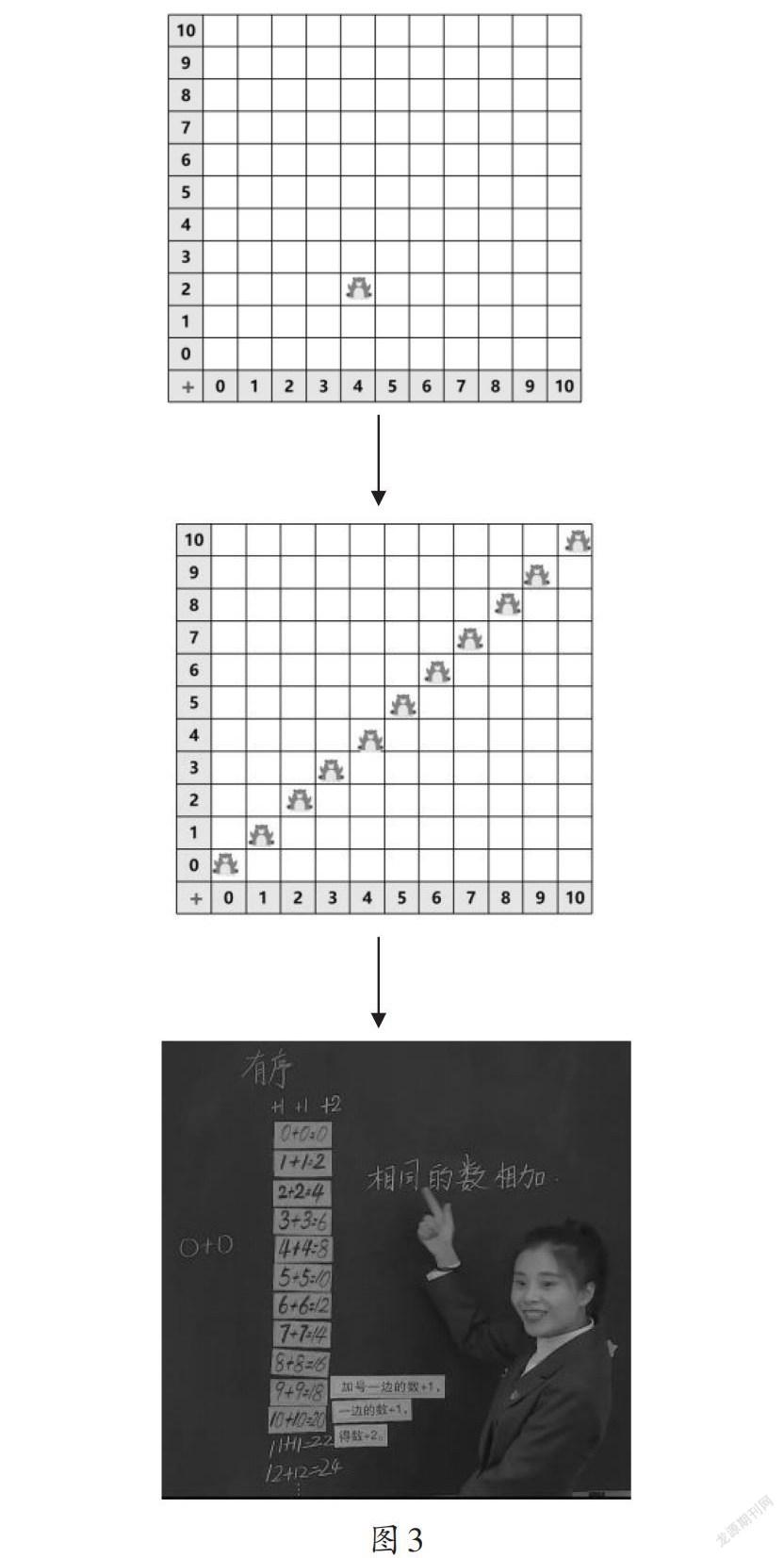
在教學“20以內的加法”后，筆者團隊設計了一節練習課“數學好玩之打地鼠——20以內的加法練習”，其中有這樣一個情境（如圖3）：

對于零星出現的幾只地鼠，能說出地鼠所代表的算式和結果，便算作打地鼠成功。在學生熟悉游戲規則后，教師出示一串地鼠，問：“你能用一個算式，便打掉這一串地鼠嗎？”學生通過觀察，發現這一串地鼠對應的算式都是相同加數相加，于是給出了各種各樣的答案：（）+（）、○+○、△+△、☆+☆……甚至有學生寫出“A+A”的算式。在這里，教師當然不需要教學用字母表示數，但是學生已經能夠初步意識到相同的符號可以代表相同的數，并且能用這樣一個高度抽象的算式概括這一串算式，甚至還能超越表格，想到11+11、12+12、100+100……

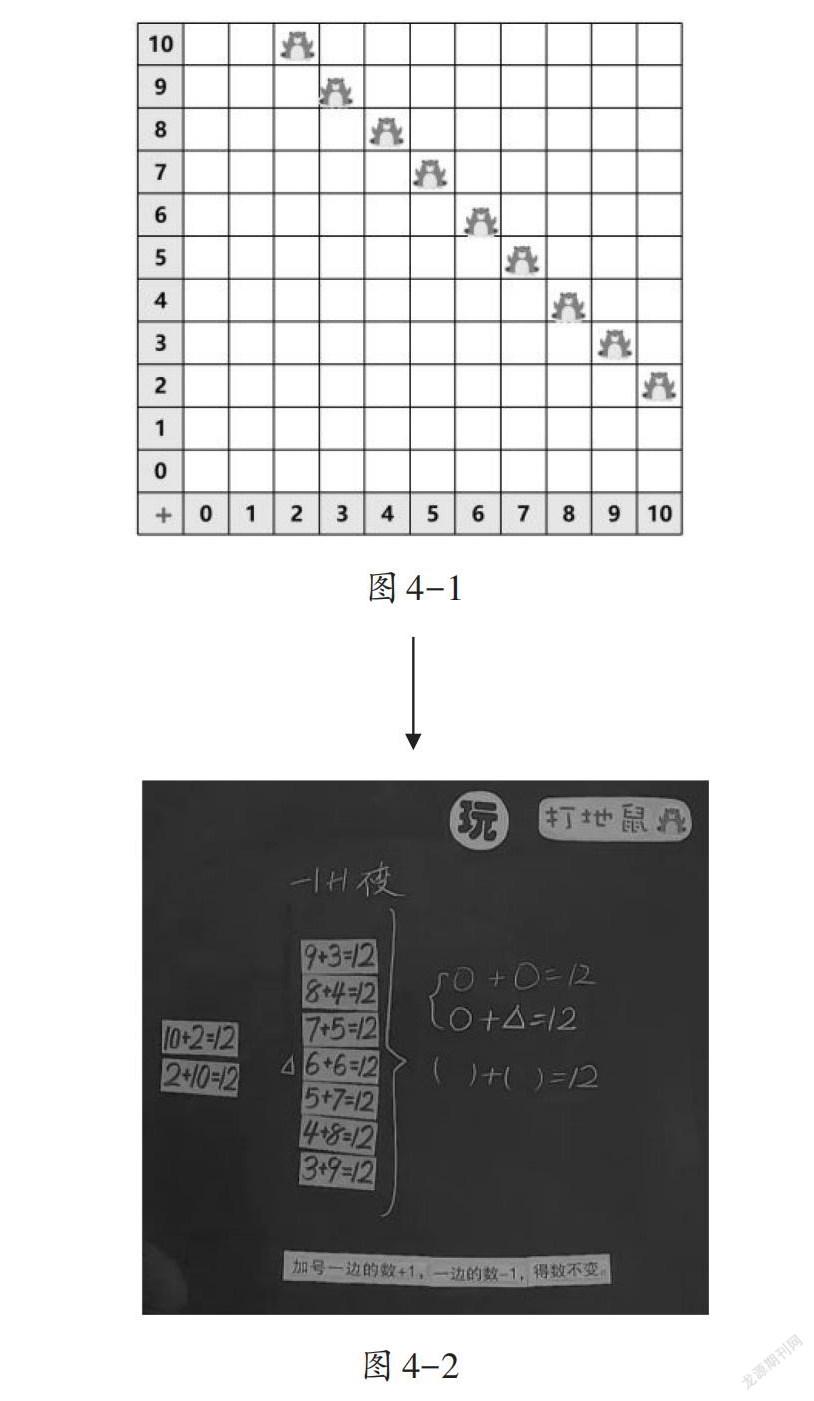
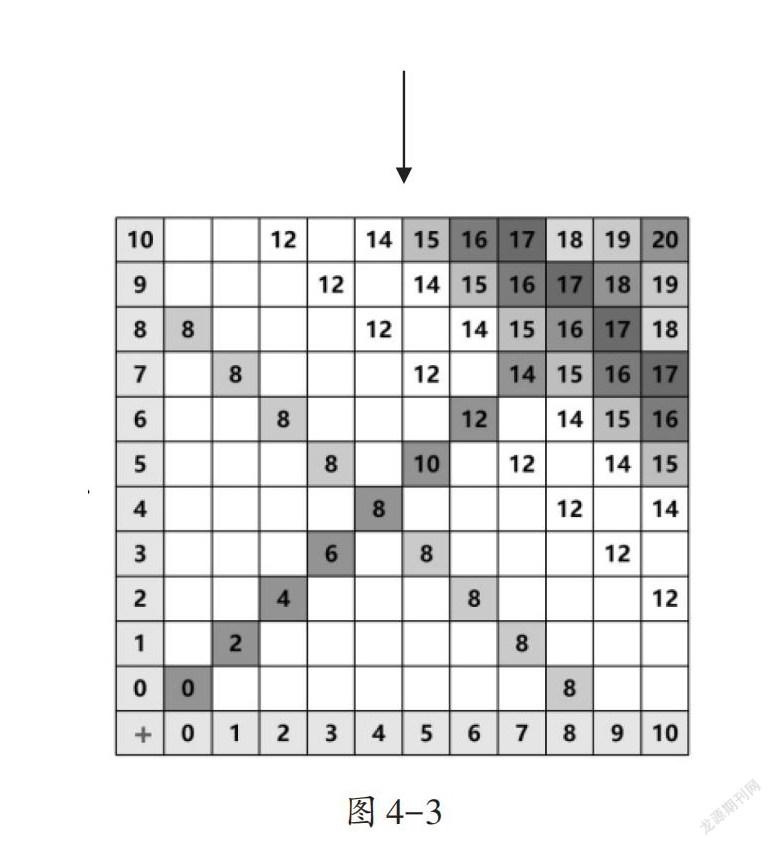
教師出示一串地鼠（如圖4-1），學生觀察后發現地鼠所代表的算式的和都為12。哪如何用一個算式表示呢？學生能很快想到用符號來代替（如圖4-2），找出這一組算式的算式之王——10+2與2+10，并發現其他算式看起來雖然不是10+2，但在計算的時候都能轉化成10+2。最后，教師再給出幾串有規律的地鼠，以對角線為對稱軸形成對稱圖形（如圖4-3）。這樣，即使在一年級時不教學對稱的含義，也可以讓學生初步感受數學的對稱之美。

本課用“怎樣才能做到一下打一串”的任務驅動學生感受相同的符號可以代表相同的數，學生的代數思維由此萌芽了。本節課作為一節練習課，卻通過這樣游戲化的情境，達到了寓教于樂的教學目的。

3.讓符號承載起文化的浸潤

【案例4】除法豎式為什么與眾不同？基于算理深化對運算符號的認識

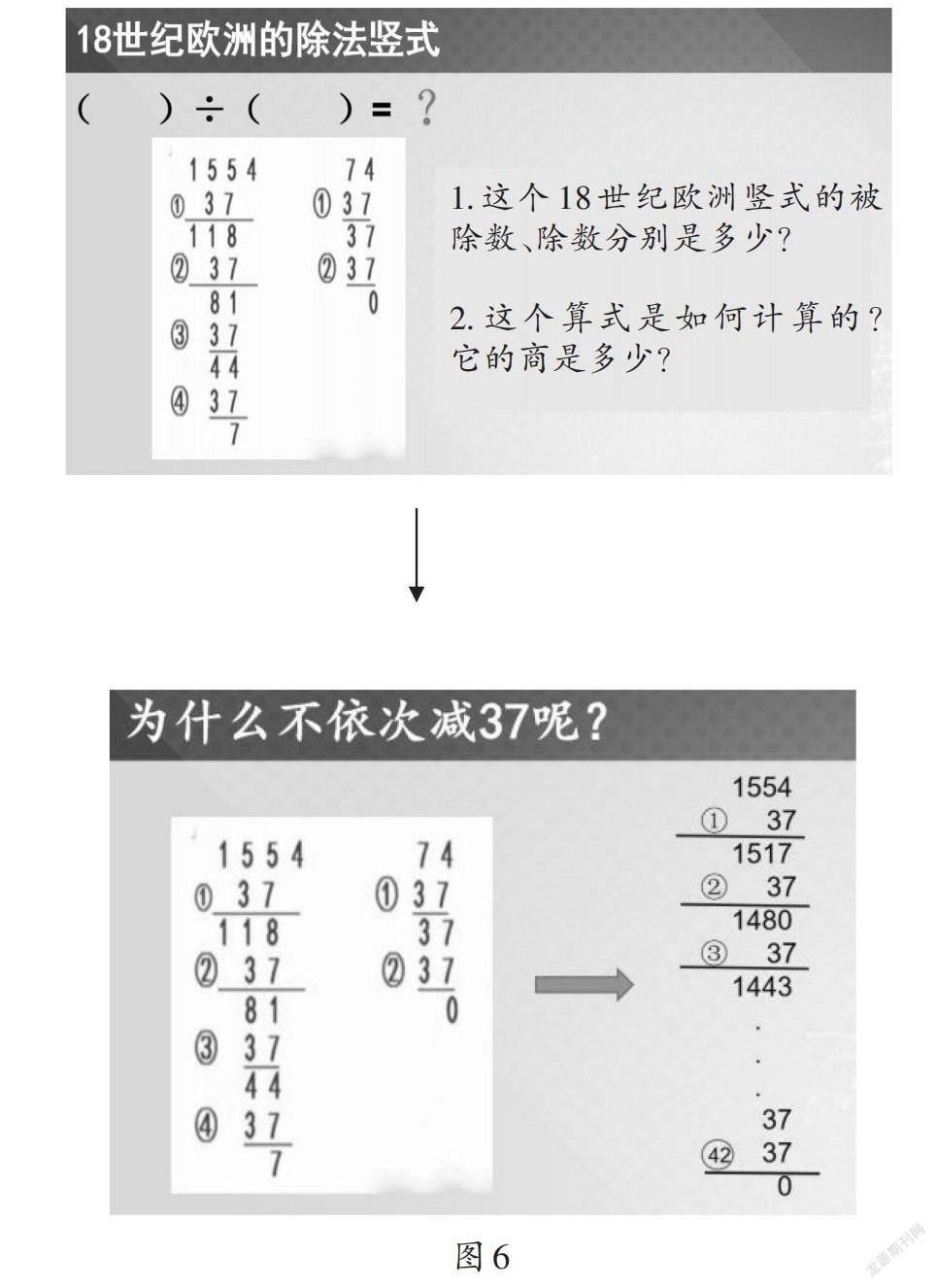
“+、-、×、÷”作為現在常用的四種運算符號，也有著深厚的歷史淵源：“+”號是由拉丁文“et”（“和”的意思）演變而來的；“-”號是從拉文“minus”（“減”的意思）演變而來的;“÷”的使用，可以追溯到1630年英國人約翰·比爾的著作，人們推測他是將阿拉伯人的除號“-”與比的記號“∶”合并轉化而成的；18世紀，美國數學家歐德萊把“×”作為乘號，他認為“×”是“+”斜起來的另一種表示增加的符號。如此可見，每一個看似簡單的數學符號都承載著深厚的數學文化。同理，對于加、減、乘、除的豎式計算，只有“÷”演變為了“[]”，這是為什么？對此，筆者團隊設計了一節課——“除法豎式的變遷”，以幫助學生基于算理來認識與理解除法豎式里的符號變遷。

課前出示任務（如圖5）：完成四道豎式計算，想一想，哪一道算式最特別，為什么？

絕大部分學生認為除法豎式最特別：一是書寫格式不同，加、減、乘法都是從上往下計算并記錄，而除法是先里后外，一會兒上一會兒下；二是除法的運算順序不同，加、減、乘法都是從低位開始計算，而除法是從高位開始計算。正因為除法的與眾不同，也因為除法的計算里還包括了乘法和減法的計算，因此在四種運算中，學生計算除法的出錯率是最高的。如何更好地幫助學生基于算理的理解來提高除法運算的正確率？研究除法豎式里的符號變遷，是一條可行之路。

通過研究18世紀歐洲的除法豎式（如圖6），學生就能感受到計算除法實際上就是在做減法，每次減去相同的減數；初步感知到，為了計算方便，就要先減去更多的部分，也就是為什么除法會從高位開始計算。正如我們在生活中進行估算時也是先從高位開始估。

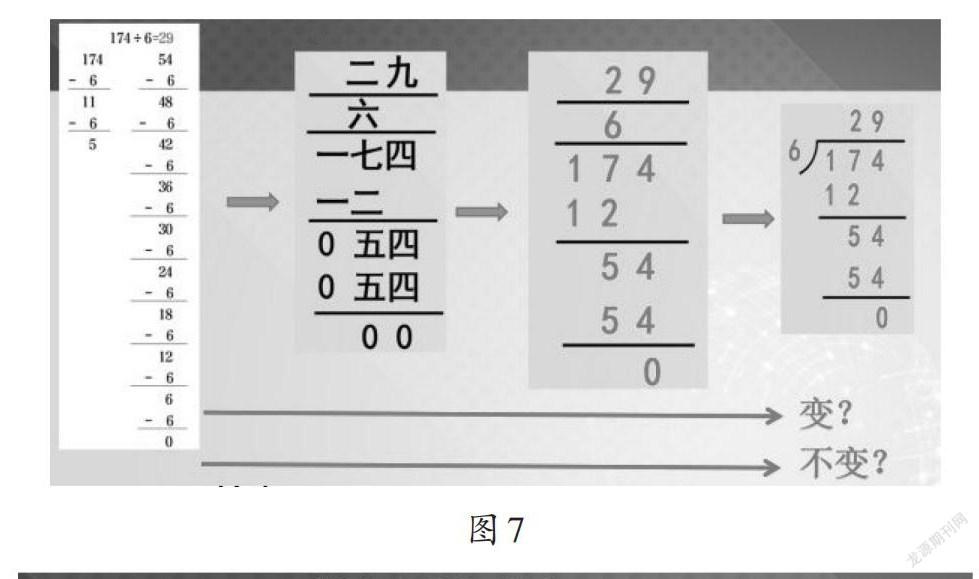
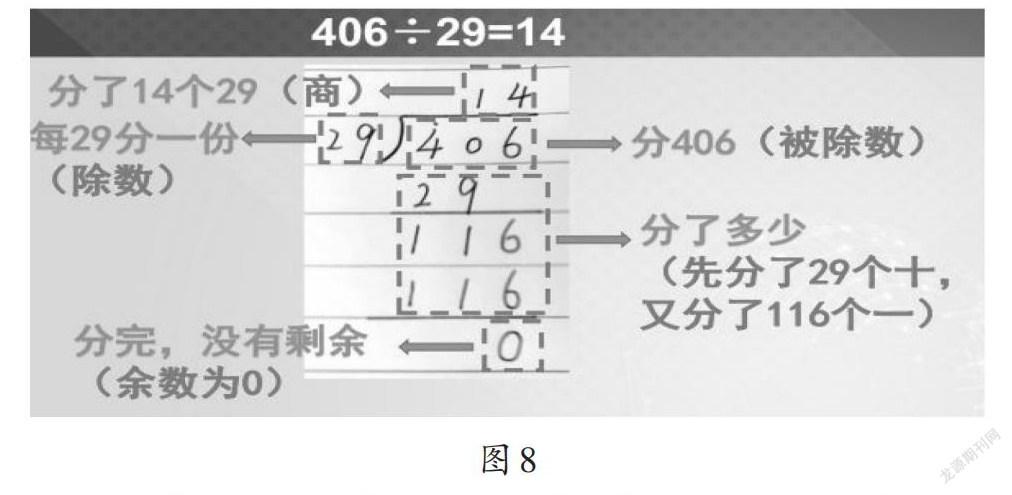
如圖7所示，通過觀察“174÷6”的除法豎式的演變，學生感受到“÷”在豎式里演變成“[]”是為了更好地記錄除法計算的過程；變的是記錄的格式，不變的是除法就是減法的計算本質。而除法豎式與眾不同之處，是除法豎式需要記錄除法的5件事：分誰？怎么分？分了多少？分的結果是什么？還有剩嗎？（如圖8）

因為除法豎式需要記錄5件事，所以才會有與眾不同的記錄方式。這節課面向四年級學生時就做到“除到有余數為止”；到了五年級的小數除法，就是將剩余的數細化計數單位后進行再分再減，基于算理的理解便將整數除法與小數除法打通了。

這樣一節數學文化課，表面上是探究除法豎式中的符號變遷，實質卻是基于算理的理解強化學生符號意識與運算能力的培養。

再看以上幾個教學案例，每一個看似冰冷而抽象的數學符號，都經歷了數學家與整個人類的火熱思考。數學教學中，教師首先要了解每個數學符號的來龍去脈，再帶領學生去經歷數學符號的再創造，只有這樣才能培養學生的符號意識。因為只有讓每一個數學符號都綻放出數學思維的光芒，學生的符號意識才能根植于心。

（責編 金 鈴）