可公開驗證無對運算的無證書聚合簽密方案

陳 虹，周 沫+，侯宇婷，趙菊芳，肖成龍，郭鵬飛

1.遼寧工程技術大學 軟件學院，遼寧 葫蘆島125105

2.汕頭大學 計算機系，廣東 汕頭515063

簽密是在同一個操作步驟內實現公鑰加密和數字簽名兩種功能，并保證消息的機密性和認證性。與簽名和加密先后在兩個步驟內完成的方式相比，簽密的運算代價和通信開銷大幅度降低，且安全系數和效率更高。1997年，Zheng[1]提出了簽密的思想，并給出了具體的方案設計，滿足消息的機密性和不可否認性。2002 年，Baek 等[2]提出了安全模型，用于驗證簽密方案是否滿足自適應選擇密文攻擊下的語義安全性和自適應選擇消息攻擊下的不可偽造性。同年，Malone-Lee[3]將簽密技術應用到基于身份的密碼體制中設計了一個簽密方案，但該方案的語義安全性后來被證明是不滿足的。2005年，Chen等[4]也提出了一個基于身份密碼體制的簽密方案，并在雙線性Diffie-Hellman假設下證明了其安全性。將簽密技術與實際應用環境相聯系，研究人員提出了不同種類的簽密方案[5-10]。當簽密用戶較多，簽密數量較大，接收者需要同時驗證多個密文時，普通的簽密方案不能達到理想的運算效率。聚合簽密能夠將多個簽密消息合并為一個，減少密文驗證的時間，非常適用于車載自組織網絡、智能電網等計算資源和帶寬受限的環境。2009年，Selvi等[11]結合聚合簽名的思想設計了一個基于身份密碼體制的聚合簽密方案，提高了密文的批驗證效率。2020年，Abouelkheir等[12]也提出了一個基于身份的聚合簽密方案，并在橢圓曲線離散對數問題的假設下證明了安全性。但在上述方案中，用戶私鑰由私鑰生成中心（private key generator，PKG）設置，存在著安全隱患，在實際應用中顯露弊端。

2003 年，Al-Riyami 等[13]提出了更為安全的無證書密碼體制，取消了公鑰證書，解決了證書管理的過程復雜、代價高等問題，同時也克服了密鑰托管問題，用戶私鑰不再由PKG統一設置，而是由密鑰生成中心（key generation center，KGC）和用戶合作生成。2011 年，Lu 等[14]提出了一個無證書聚合簽密（certificateless aggregate signcryption，CLASC）方案，將聚合的思想應用到無證書簽密中，凸顯其優勢。就此CLASC 成為研究熱點，如何在保證方案安全性與可行性的同時，減小運算代價成為設計難題。之后，國內外學者提出了大量的CLASC方案，如Eslami等[15]、張玉磊等[16]和劉建華等[17]提出的CLASC方案。上述方案在簽密及驗證階段需要進行大量的雙線性對運算和指數運算，這兩種運算與點乘運算相比，代價極高。蘇靖楓等[18]和李晨等[19]提出的CLASC 方案，雖沒有使用效率較低的雙線性對運算，但在解簽密階段需要4n次點乘運算，以及胡榮磊等[20]提出的物聯網環境下的CLASC 方案，在解簽密階段需要5n+1次點乘運算，運算效率仍有待提升。將聚合簽密的優點應用于異構網絡中，牛淑芬等[21]和劉祥震等[22]提出了異構聚合簽密方案，實現了異構密碼環境中的“多對一”傳輸，但在簽密驗證階段使用了雙線性對運算，效率較低。

傳統公鑰密碼體制下的簽密需要證書機構（certificate authority，CA）頒發公鑰證書，證書管理的成本較高，不適合大規模應用；基于身份的簽密將用戶的公鑰與身份解綁，消除了公鑰證書，但存在密鑰托管問題，PKG 持有所有用戶的私鑰；無證書簽密既無CA 也無密鑰托管問題，更安全更高效，現階段對簽密的研究主要基于無證書的密碼體制。簽密的傳輸模式也從最開始“一對一”的傳輸逐漸發展為“多對一”的聚合傳輸，聚合簽密可聚合傳輸且能批量驗證，大大降低了通信開銷。大多數的聚合簽密方案都使用了雙線性對運算，安全性得到了保證但運算速度較慢。基于橢圓曲線離散對數的聚合簽密方案雖不含雙線性對，效率較高，但安全程度略有降低。

為了提高無證書聚合簽密的運算效率，本文基于Qu 等[23]提出的安全性強且效率較高的簽名方案，構造了一個新的可公開驗證無對運算的CLASC 方案。主要工作可分為以下三方面。

（1）構造了一個可公開驗證無對運算的CLASC方案，該方案基于無證書密碼體制，避免了使用代價較高的CA，且無密鑰托管問題。未使用雙線性對運算和指數運算，僅使用點乘運算。

（2）對本文方案進行了完整的安全性證明，結果表明，該方案在隨機預言模型下滿足安全性，并具有公開驗證性。

（3）從理論分析方面對本文方案進行了評估，將該方案與六個相關的聚合簽密方案進行了比較，結果表明，該方案在解簽密階段只需要3n次點乘運算，運算效率較高。并對該方案進行了仿真實驗，實驗結果表明，聚合簽密極大地提高了密文的驗證效率。

1 預備知識

1.1 困難性問題

（1）計算性Diffie-Hellman（computational Diffie-Hellman，CDH）問題：已知G是橢圓曲線上的加法循環群，G的階為大素數q，生成元為P，CDH問題是指給定元組(P,aP,bP)，其中a,b∈未知，求解abP的值。

（2）離散對數（discrete logarithm，DL）問題：已知G是橢圓曲線上的加法循環群，G的階為大素數q，生成元為P，DL 問題是指給定元組(P,aP)，其中a∈未知，求解a的值。

1.2 無證書聚合簽密方案定義

CLASC 方案的參與方有三個，分別為KGC、簽密者IDi(1 ≤i≤n)和接收者IDB。具體算法如下：

（1）系統參數生成：輸入安全參數k，KGC 輸出系統主密鑰x和參數params，保密x，公開params。

（5）聚合簽密：輸入n個簽密密文σi，聚合簽密者計算并輸出聚合簽密密文σ。

1.3 無證書聚合簽密方案的安全模型

CLASC 方案的安全模型存在兩類敵手[13]：一類模擬惡意的用戶，可以將用戶原有的公鑰進行替換，但不能得知系統主密鑰；另一類模擬惡意的KGC，可以得知系統主密鑰，但不能進行替換用戶公鑰的操作。因此，CLASC 方案的安全性需考慮在兩類敵手攻擊下的保密性和不可偽造性。以敵手A1為例，敵手與挑戰者C之間的交互如圖1、圖2所示。

圖1 適應性選擇密文攻擊的示意圖（敵手A1）Fig.1 Schematic diagram of adaptive chosen ciphertext attack(adversary A1)

圖2 適應性選擇消息攻擊的示意圖（敵手A1）Fig.2 Schematic diagram of adaptive selection message attack(adversary A1)

定義1（敵手A1攻擊下的保密性）如果不存在任何多項式數量級的敵手A1能夠在下面的游戲中以不可忽略的優勢獲勝，那么稱該方案具有適應性選擇密文攻擊下不可區分的安全屬性（indistinguishability under adaptive chosen ciphertext attack，IND-CCA2）。

系統參數生成：輸入安全參數k，挑戰者C運行系統參數生成算法，生成系統參數params和系統主密鑰，并將params發送給敵手A1。

第一階段問詢：敵手A1可適應性地進行以下多項式數量級的問詢：

（1）部分私鑰問詢：A1輸入用戶身份IDi進行問詢，C返回IDi的部分私鑰。

（2）公鑰問詢：A1輸入用戶身份IDi進行問詢，C返回IDi的公鑰。

（3）秘密值問詢：A1輸入用戶身份IDi進行問詢，C返回IDi的秘密值。

（4）公鑰替換問詢：A1輸入用戶身份IDi和新公鑰進行問詢，C將IDi現有公鑰進行替換并記錄。

（5）簽密問詢：A1輸入消息mi、簽密者身份IDi和接收者身份IDB進行問詢，C返回密文σi。

（6）聚合簽密問詢：A1輸入消息mi、簽密者身份IDi和接收者身份IDB進行問詢，C返回聚合密文σ。

（7）解簽密問詢：A1輸入簽密σi和接收者身份IDB進行問詢，C返回消息mi。

挑戰：經過足夠的問詢后，A1選擇兩個長度相等的明文mi(i∈{0,1})和用戶身份IDi、IDB。C判斷IDB是否為挑戰對象，若不是則拒絕；否則，C隨機選擇一個比特b，對明文消息mb進行簽密得到密文σ*，返回給A1。

第二階段問詢：與第一階段問詢類似，不同之處在于不能進行IDB的部分私鑰問詢和σ*的解簽密問詢。

猜測階段：A1給出一個猜測值b′，若b′=b，則敵手A1取得游戲勝利。

定義2（敵手A2攻擊下的保密性）如果不存在任何多項式數量級的敵手A2能夠在下面的游戲中以不可忽略的優勢獲勝，那么稱該方案具有適應性選擇密文攻擊下不可區分的安全屬性（IND-CCA2）。

系統參數生成：輸入安全參數k，挑戰者C運行系統參數生成算法，將生成的系統參數params和主密鑰都發送給敵手A2。

第一階段問詢與定義1類似，不同之處在于不能進行公鑰替換問詢和部分私鑰問詢。

第二階段問詢與定義1類似，不同之處在于不能進行IDB的秘密值問詢。

挑戰階段和猜測階段與定義1相同。最終，敵手A2取得游戲勝利。

定義3（敵手A1攻擊下的不可偽造性）如果不存在任何多項式數量級的敵手A1能在下面的游戲中以不可忽略的優勢獲勝，那么稱該方案具有適應性選擇消息攻擊下不可偽造的安全屬性（existential unforgeability under adaptive chosen messages attack，EUF-CMA）。

系統參數生成和問詢階段與定義1相同。

定義4（敵手A2攻擊下的不可偽造性）如果不存在任何多項式數量級的敵手A2能夠在下面的游戲中以不可忽略的優勢獲勝，那么稱該方案具有適應性選擇消息攻擊下不可偽造的安全屬性(EUF-CMA)。

系統參數生成和問詢階段與定義2 相同。偽造階段與定義3相同。最終，敵手A2取得游戲勝利。

2 本文無證書聚合簽密方案

本文構造的CLASC 方案包括系統參數生成、部分密鑰設置、用戶密鑰設置、簽密、聚合簽密、解簽密和聚合解簽密七個部分。以簽密過程為例，本文CLASC方案如圖3所示。

圖3 本文CLASC方案Fig.3 CLASC scheme of this paper

方案具體如下：

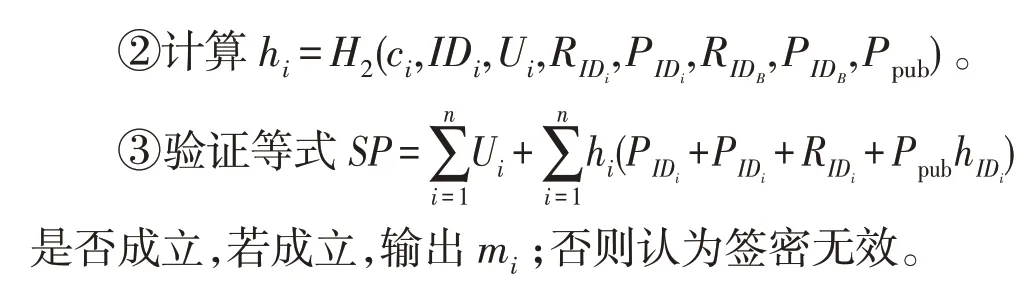
3 本文方案安全性分析

3.1 正確性

（1）密鑰的正確性

用戶IDi通過以下等式驗證部分密鑰是否有效：

（2）消息的正確性

接收者IDB通過以下等式驗證消息mi的正確性：

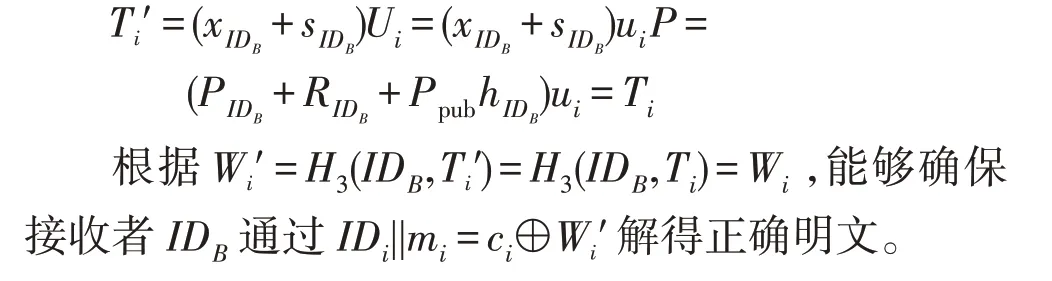
（3）簽名的正確性

接收者IDB通過以下等式驗證簽名的正確性：

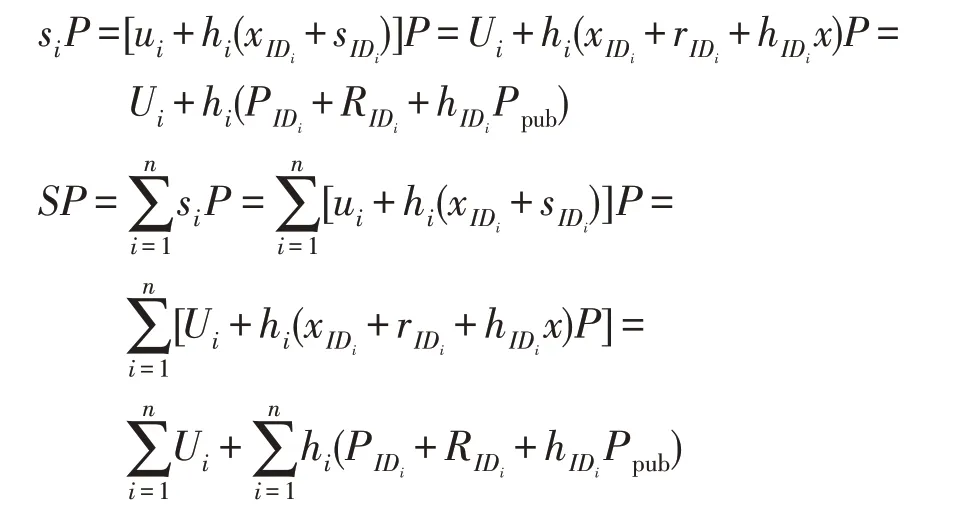
若等式成立，則發送者身份驗證成功，消息mi能夠被接收。

3.2 公開驗證性

3.3 機密性

若存在敵手A1、A2具有不可忽略的獲勝優勢的情況，則A1、A2具有幫助挑戰者C破解困難問題的能力。

引理1（敵手A1攻擊下的保密性）在隨機預言模型中且CDH 問題難解的情況下，根據定義1 知敵手A1攻擊成功的優勢是可忽略的。如果在概率多項式時間內，A1能夠以不可忽略的優勢ε（最多經過qi（i=1,2,3）次Hi問詢、qpsk次部分私鑰問詢、qs次簽密問詢、qun次解簽密問詢等）贏得游戲IND-CLSCCCA2，那么就存在挑戰者C在概率多項式時間內以概率的優勢解決CDH困難問題。

證明如果A1能夠以不可忽略的優勢贏得游戲IND-CLSC-CCA2，則C能夠在A1的幫助下成功解決CDH 問題。其中，C在游戲中的角色為挑戰者，A1為C的子程序。即已知{P,aP,bP}，求abP的值。

（1）系統參數生成：C運行系統參數生成算法，設置Ppub=aP，將參數params發送給敵手A1。

（2）問詢階段：A1進行以下問詢，并將問詢的值記錄在各列表中，所有列表初始化為空。

A1收到σ*后繼續問詢，與問詢階段類似，不同之處在于不能進行IDB的部分私鑰問詢和σ*的解簽密問詢。經足夠的問詢后，A1輸出對b的猜測b′，若b′=b，則C輸出作為CDH問題的解，其中，

若A1進行過IDB的部分私鑰問詢，進行過H2問詢，進行過的H3問詢，則游戲失敗。A1未進行過部分私鑰問詢的概率至少為1/q1，未進行過H2問詢的概率至少為1/q2，未進行過的H3問詢的概率至少為1/q3，且挑戰者C未拒絕有效簽密的概率至少為，則C成功解決CDH問題的概率為因為A1贏得游戲的優勢是可忽略的，所以C成功解決CDH 困難問題的前提條件不存在。根據定義1所述，本文方案具有保密性。證畢。

引理2（敵手A2攻擊下的保密性）在隨機預言模型中且CDH 問題難解的情況下，根據定義2 知敵手A2攻擊成功的優勢是可忽略的。如果在概率多項式時間內，A2能夠以不可忽略的優勢ε（最多經過qi（i=1,2,3）次Hi問詢、qpsk次秘密值問詢、qs次簽密問詢、qun次解簽密問詢等）贏得游戲IND-CLSCCCA2，那么就存在挑戰者C在概率多項式時間內以概率的優勢解決CDH困難問題。

證明如果A2能夠以不可忽略的優勢贏得游戲IND-CLSC-CCA2，則C能夠在A2的幫助下成功解決CDH 問題。其中，C在游戲中的角色為挑戰者，A1為C的子程序。即已知{P,aP,bP}，求abP的值。

（1）系統參數生成：C運行系統參數生成算法，設置Ppub=xP，將參數params和x發送給敵手A2。

（2）問詢階段：A2進行以下問詢，并將問詢的值記錄在各列表中，所有列表初始化為空。

3.4 不可偽造性

引理3（敵手A1攻擊下的不可偽造性）在隨機預言模型中且DL 問題難解的情況下，根據定義3 知敵手A1攻擊成功的優勢是可忽略的。如果在概率多項式時間內，A1能夠以不可忽略的優勢ε（最多經過qi（i=1,2,3）次Hi問詢、qpsk次部分私鑰問詢、qs次簽密問詢、qun次解簽密問詢等）贏得游戲EUF-CMA，那么就存在挑戰者C在概率多項式時間內以概率的優勢解決DL困難問題。

證明如果A1能夠以不可忽略的優勢贏得游戲EUF-CMA，則C能夠在A1的幫助下成功解決DL 問題。其中，C在游戲中的角色為挑戰者，A1為C的子程序。即已知{P,aP}，求a的值。

初始化階段與問詢階段同引理1。

引理4（敵手A2攻擊下的不可偽造性）在隨機預言模型中且DL 問題難解的情況下，根據定義4 知敵手A2攻擊成功的優勢是可忽略的。如果在概率多項式時間內，A2能夠以不可忽略的優勢ε（最多經過qi（i=1,2,3）次Hi問詢、qpsk次秘密值問詢、qs次簽密問詢、qun次解簽密問詢等）贏得游戲EUF-CMA，那么就存在挑戰者C在概率多項式時間內以概率的優勢解決DL困難問題。

證明如果A2能夠以不可忽略的優勢贏得游戲EUF-CMA，則C能夠在A2的幫助下成功解決DL 問題。其中，C在游戲中的角色為挑戰者，A2為C的子程序。即已知{P,aP}，求a的值。

初始化階段與問詢階段同引理2。

因此，C成功解決了DL 問題。A2未進行過秘密值問詢的概率至少為，A2偽造的簽密為一個有效的聚合簽密且z1=0，zi=1(2 ≤i≤n)的概率至少為εδ(1-δ)n-1，則C成功解決DL 問題的概率為因為A2贏得游戲的優勢是可忽略的，所以C成功解決DL困難問題的前提條件不存在。根據定義4 所述，本文方案具有不可偽造性。證畢。

4 本文方案性能效率分析

4.1 理論分析

將本文方案與聚合簽密方案文獻[12，18-21，24]的運算效率和安全性進行比較，假設參與簽密的用戶共有n個，e 表示指數運算，s 表示群G上的點乘運算，p 表示雙線性對運算。相比較以上三種運算，哈希運算、異或運算和加法運算的耗時對整體效率的影響可以忽略不計。方案分析結果如表1所示。

從表1可以看出，當消息個數為1個時，文獻[21，24]的運算總量分別為e+4p+2s 和e+3p+5s，都使用了指數運算、雙線性對運算和點乘運算。根據Cao等[25]的實驗表明，一次雙線性對運算所需要的計算代價約為一次點乘運算的20 倍，一次指數運算所需要的計算代價約為一次點乘運算的3 倍。就計算代價而言，本文方案的計算代價遠遠小于以上兩種方案。文獻[12，18-20]和本文方案一樣只使用了點乘運算，其中文獻[19-20]在各個階段的運算量都比本文方案大，而文獻[12，18]雖然在簽密階段的運算量和本文方案相同，但在解簽密階段的運算量分別比本文方案多出一次和兩次點乘運算，運算代價仍比本文方案高。

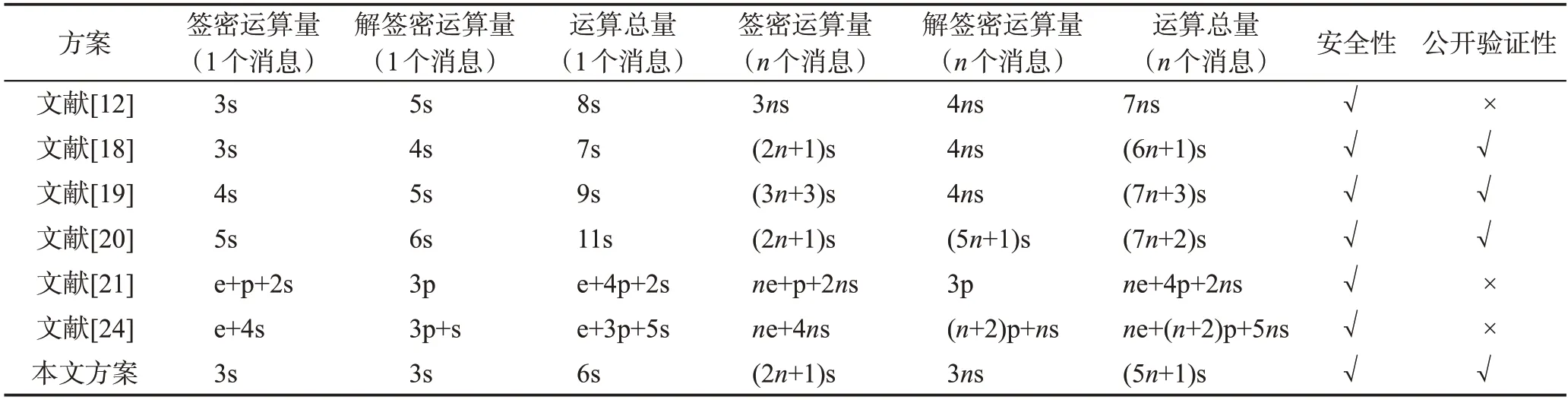
表1 簽密方案運算效率與安全性比較Table 1 Comparison of efficiency and security of signcryption schemes

當消息個數為n個時，本文方案的計算代價依舊遠遠小于使用了復雜運算的文獻[21，24]。文獻[12，19]的運算總量分別比本文方案多出2n-1 和2n+2次點乘運算，無論是簽密階段還是解簽密階段，本文方案的運算效率都更高。文獻[18，20]雖然在簽密階段的運算量和本文方案相同，但在解簽密階段的運算量分別比本文方案多出n和2n+1 次點乘運算，運算代價仍比本文方案高。文獻[21]在聚合簽密驗證階段，需要使用Rsj的值，即根據接收者的私鑰計算，任意第三方無法計算該值；文獻[24]在聚合簽密驗證階段，需要使用ri的值，即根據接收者的私鑰計算，任意第三方也無法計算該值；文獻[12]在簽密的驗證階段雖然不需使用用戶的私鑰，但需使用明文消息，如果進行公開驗證會泄露明文消息，因此上述方案均不滿足公開驗證性。綜上，本文方案具有明顯優勢。

4.2 仿真實驗分析

實驗環境：Intel Core i5-5200U@2.20 GHz CPU，4 GB RAM，Windows 10操作系統，python 3.6.8。

實驗結果分析：用戶身份IDi唯一，明文消息|m|長度隨機，消息個數n分別取1、5、10、20、50、100、200，實驗結果包括n個消息的簽密時間和解簽密時間，如圖4、圖5所示。

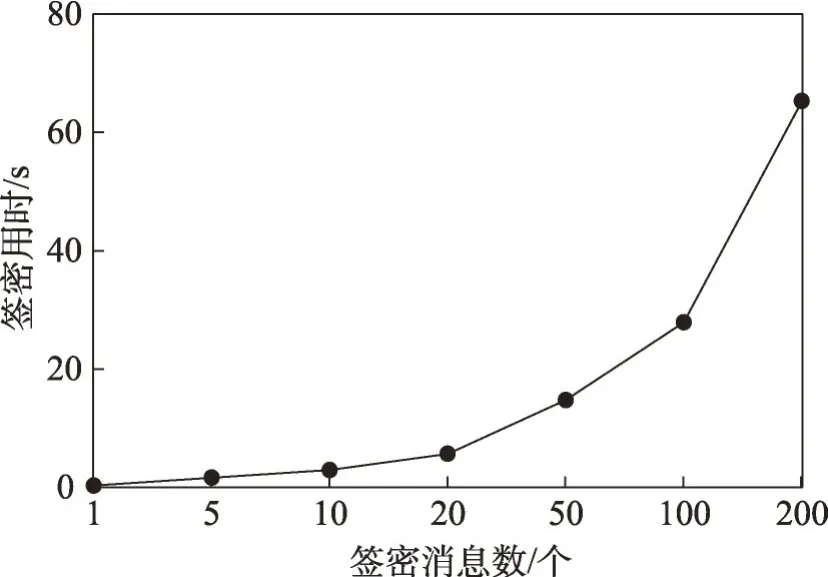
圖4 簽密效率Fig.4 Signcryption efficiency

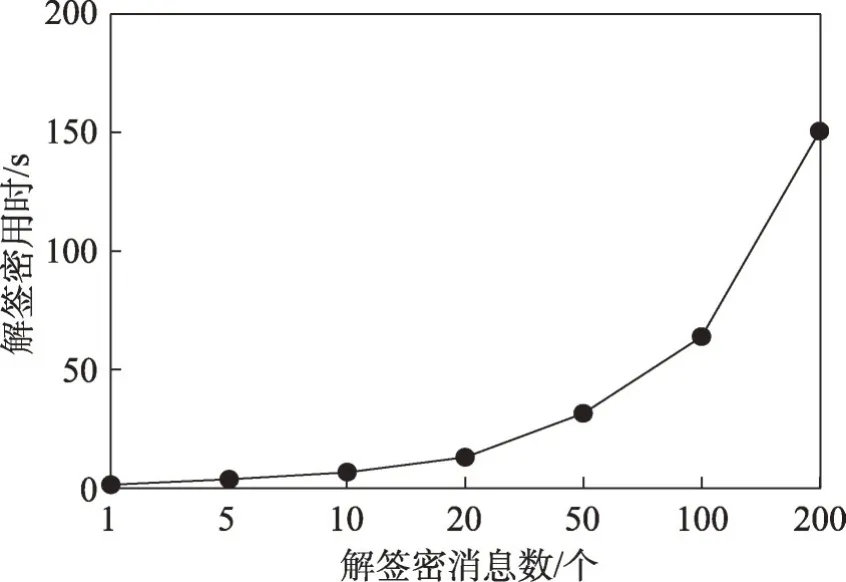
圖5 解簽密效率Fig.5 Efficiency of de-signcryption

解簽密用時分別為1.390s、3.655 s、6.655 s、12.999 s、31.533 s、63.823 s、150.559 s，實驗結果表明聚合密文解簽密的時間約為n個密文分別解簽密時間的1/2，極大提高了密文的驗證效率。

5 案例設計

本文方案可以應用在智能交通系統中，車載自組織網絡（vehicular ad hoc network，VANET）是智能交通系統的基礎。VANET是一種將網絡節點建立在汽車和道路基礎設施上的分布式、動態變化的無線自組織通信網絡。VANET 結構包括服務中心、車載單元（on board unit，OBU）和路邊單元（road side unit，RSU）三部分。服務中心為信任機構，擁有最高的管理權限，負責OBU和RSU的登記管理。OBU安裝在每輛車上，RSU安裝在道路兩側或十字路口，OBU與OBU、OBU與RSU之間通過無線信道進行通信，構成一個無線自組織通信網絡。VANET結構如圖6所示。

圖6 VANET結構Fig.6 VANET structure

由于VANET 節點多、規模大，且無線網絡本身的脆弱性和開放性，VANET 很容易受到攻擊，如竊聽、篡改、跟蹤和用戶隱私泄露等，信息安全問題嚴重阻礙其發展。簽密技術能夠較好滿足VANET 中信息傳輸的保密性、認證性等安全需求。

智能化交通系統中，1個RSU通常需要管轄上百輛車輛，要求RSU在短時間內驗證大量簽密消息，對RSU 的硬件和成本挑戰過高，需要一種快速高效的驗證技術用于大批量密文驗證。本文提出的CLASC方案是能夠進行壓縮和批處理的聚合簽密方案，可應用于OBU 與RSU 之間通信。方案中的n個簽密者為VANET 中的n個OBU，接收者為RSU，n個OBU 產生n個簽密消息并進行聚合，將聚合簽密消息發送給RSU，由RSU進行驗證并解簽密，能夠有效降低計算與通信開銷，確保消息傳遞的安全性及有效防止偽造消息。

6 結束語

本文基于Qu 等[23]提出的簽名方案，構造了一個可公開驗證無對運算的CLASC 方案，與運算時間約為點乘20倍的雙線性對運算相比，效率更高。同時，在隨機預言模型下，該方案被證明滿足安全性，并能夠驗證發送者的身份是否合法。對比其他6個方案，該方案性能更佳，可以很好地應用于計算資源和帶寬受限但安全性需求較高的環境中。聚合簽密提高了用戶較多情況下的簽密和解簽密的效率，但如何在滿足安全性的前提下，構造更為高效的聚合簽密方案仍是日后研究的重點。