小學高年級數學應用題解題能力的培養

高培利

(山東省沂水縣第五實驗小學，山東臨沂，276400)

在進行小學高年級數學教學過程中，數學應用題既是教學的難點，又是教學的重點，大多數學生在考試過程中，往往會因為各種各樣的原因導致應用題丟分.對于小學生而言進行應用題的學習，既能夠培養他們的綜合思維能力，又能夠幫助他們在日常生活中更好地去運用所學的數學知識，因此需要就小學生的數學應用題解題能力進行培養.對此，本文將首先提出目前小學高年級學生數學應用題解題能力培養過程中的問題，進一步探索有哪些合適的教學方法能夠強化培養學生的數學應用題解題能力.

1 小學高年級數學應用題解題能力培養問題

1.1 缺乏良好的數學基礎

雖然大多數小學生在正式上小學之前都會進入幼兒園進行學前教育.但是目前來說我國幼兒園能夠提供的學前教育多是啟蒙教育，即對學生的生活常識，學習興趣的啟蒙，而真正能夠讓學生接觸到的數學知識幾乎為零，因此對于大多數學生而言，其數學基礎是從進入小學之后才正式開始培養的，這就導致大多數學生缺乏良好的數學基礎，只有極少數對于數學十分感興趣，且學習數學十分認真的學生，能夠在小學階段擁有極為扎實的數學基礎.那么在這樣的情況下，因為學生自身的數學基礎不夠牢固，所以在進行數學應用題解題的過程中難以發現應用題所考核的對應的數學知識點，解題思路錯誤，解題方法不正確等等問題.

1.2 缺乏濃厚的解題興趣

目前來說，大多數數學教師在進行數學應用題講解的時候，往往會更加注重解題思路的講解，而僅僅是單一地去講解某一道應用題的解題思路，這對于學生而言是一個極為枯燥的過程，所以大多數學生對于聽教師講應用題是不太感興趣的，很容易走心，使得教師授課的效果大打折扣，也很難通過課堂教學的方式去培養學生的數學應用題解題能力.同時對于部分學生而言，完成數學應用題本身就是一項比較困難的任務，再加上數學應用題是非常容易出錯的數學題目，因此也會使得部分學生缺乏解答數學應用題的興趣.當學生對于某一件事物失去興趣之后，再想要讓學生能夠在這件事物上獲得良好的學習效果，必然是難以實現的.因此想要提高學生的數學應用題解題能力，必然需要解決學生缺乏濃厚解題興趣這一問題.

2 基于圖示法培養小學高年級數學應用題解題能力

2.1 圖示法介紹

圖示法思維可視化工具即思維導圖，又稱為心智導圖.由英國著名心理學家、教育學家東尼·博贊(Tony Buzan)在20世紀70年代所提出的，他認為思維導圖可以充分運用人體左右腦的機能，從而有效表達出人類所具有的發射性思維.常見的思維導圖主要是樹狀圖，還包括流程圖、魚骨圖、時間線等等.不同的思維導圖對于教學的輔助作用也不盡相同，比如最常見的思維導圖“樹狀圖”就更適合用于知識分類，以幫助學生梳理知識點；流程圖可用于幫助解題，讓數學解題思路更為清晰；魚骨圖可用于發散思維，從而培養學生的高級思維能力等.所以基于圖示法，去培養小學生的應用題解題能力十分有效，同時還能夠培養學生的思維能力、探索能力等.

2.2 基于圖示法進行例題解析

以圖示法培養小學高年級數學應用題解題能力時，可以把圖示法實際應用到例題講解中去，從而做到在實例中培養學生的能力.

例1已知平行四邊形的面積是320平方厘米，求梯形的面積.

圖1 例題1

這道題是小學五年級上冊“多邊形的面積”這一單元中的應用題.在進行這道題的講解時，為了能夠更加直觀的呈現出解題過程，教師可以使用“流程圖”來進行圖示法教學培養學生的應用題解題能力.

具體來說，第一步是確定現有的已知條件，即“平行四邊形的面積是320平方厘米”梯形的上底長為16厘米，下底長為20厘米；第二步是思考平行四邊形和梯形的面積公式，找出兩種圖形計算公式中的共同點，可以發現兩個公式中都存在h，而在這一例題中h又同為平行四邊形和梯形的高；第三步就是通過平行四邊形的面積來計算出h是多少；第四步是根據計算出來的h，結合梯形的上下底長度，帶入梯形面積公式中計算得出梯形的面積為288平方厘米.將以上解題思路，以“流程圖”的方式呈現出來，即為圖2所示.

圖2 流程圖

例2一輛汽車從甲地去到乙地，已經行駛了120公里，相當于全程的3/5，問從甲地到乙地一共需要行駛多少公里？

這一道題是小學六年級上冊“分數除法”這一單元的例題，在進行例題講解的時候，如果直接列出計算題，可能會讓很多學生的思維跟不上，或者是難以理解為什么要這樣計算，因此在講題的過程中，可以使用思維導圖中的“垂直線段圖”，來進行講解.那么在實際講解的過程中，首先數學教師需要闡述清楚3/5等于120公里這一思路，并在“垂直線段圖”中畫出這一部分，接著對照著圖來引導學生思考得出：已知3/5等于120公里，5/5等于從甲地到乙地，那么可以計算出1/5就等于40公里，5/5等于200公里，即從甲地到乙地的距離為200公里，最后列出算式，進行計算，方便學生能夠更好地理解算式推理過程.將以上解題思路，以“垂直線段圖”的方式呈現出來，即為圖3所示.

圖3 垂直線段圖

又如此例，一本書，第一個星期看了其內容的約1/4，第二周則看了內容的約2/5，還剩下70頁沒有閱讀，問這本書頁數總共是多少？在實際開展求解的過程當中，可以將整本書當做是單位一，實際的求解的運作過程如下圖4所示.

圖4 看書的分數應用解題圖示

3 基于情境教學法培養小學高年級數學應用題解題能力

3.1 情境教學法介紹

目前來說，小學生在進行應用題解題的時候，經常會出現思維被限制住、被固化的情況，之所以會發生這樣的情況，主要是由于數學教師在課堂上進行例題講解的時候，往往會根據教材上的知識點作為標準，而不會進行拓展.長此以往，學生的解題思維就被固定在教材的知識點上了，認為教材上的解題思路才是正確的，其他解題思路便是不正確的.

因此為了能夠讓學生更好地在數學學習中提高他們的應用題解題能力，教師可以通過創設情景的方式，去沖擊學生對于應用題解題思路的原有認知，讓學生在情境中，積極的探索全新的數學解題思路、全新的問題解決方案，使得學生對于數學問題思考的方式能夠有所拓展.

當然，設立情境的方式，不僅僅可以由數學教師在課堂上完全原創，也可以設置與生活實際關聯的新問題.而且從學生實際的生活中去設置問題情景，還能夠讓學生感受到一種更為親切的感覺，讓學生覺得這些困難的數學應用題就存在于自己的生活當中.這種親切感，會使得學生對于數學探究、鍛煉自身解題能力更有興趣，甚至能夠讓學生在日常生活中自行探究數學，來提高學生的數學自學能力.

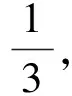
這道數學題目結合了學生的生活，將數學的計算和數量之間的關系運算結合在一起需要學生了解三者之間的數量關系，分析清楚這些數量關系之間的聯系.

3.2 基于情境教學法進行例題解析

具體來說，教師在選擇以創設情景的方式來培養學生的應用題解題能力的時候，可以加入生活化的內容進行講解.

例3一塊平行四邊形的菜地，底是35米，高是18米，這塊菜地的面積是多少？如果每平方米收青菜25千克，這塊菜地一共收青菜多少千克？

這道題是小學五年級上冊“多邊形的面積”這一單元中的應用題，為了能夠更加直觀的進行例題的講解，教師可以提前準備平行四邊形的卡紙，用具體的事物給學生進行講解，讓學生在聽課的時候能夠建立起解決圖形應用題的立體思維，從而明白平行四邊形本質上是長方形變形得到的，所以可以利用長方形的面積計算公式推出平行四邊形的面積計算公式，最終得出第一問的答案.平行四邊形面積公式=底×高，所以答案為35×18=630平方米.這一道題有兩個問題，所以在講解這道題的時候，教師還需要強調審題，要讓學生重視審題的重要性.在解決第二問的時候，題目中給出了新的解題信息，即“每平方米收青菜25千克”，所以要求這塊平行四邊形菜地的產量需要選擇公式總產量=產量×平行四邊形面積，即630×25=15 750千克.

4 結束語

總的來說，通過分析與研究后，本人發現目前小學高年級學生之所以會存在數學應用題解題能力較弱的情況，主要是因為以下三點原因：一是小學生自身的數學基礎知識不夠扎實，二是因為教師的講解方式過于枯燥，導致學生對于學習如何解題不感興趣，三是學生沒有掌握正確的應用題審題方法.那么針對以上問題，可以通過圖示法、情境教學法來開展更為直觀、有趣的數學應用題講解，從而更好地培養學生的數學解題能力.