GeoGebra在高中數學教學中的應用
——以棱柱、棱錐與棱臺的表面積為例

田 琳

(哈爾濱師范大學教師教育學院，黑龍江哈爾濱，150000)

1 問題提出

《普通高中數學課程標準(2017)》特別提及教育信息化：“信息技術是學生學習與教師教學的重要輔助手段，為師生交流、生生交流、人機交流搭建了平臺，為學習和教學提供了豐富的資源.因此，教師應重視信息技術的運用，優化課堂教學，轉變教學與學習的方式.”高中數學因其抽象和晦澀，經常成為學生學習的弱點與痛點.其中，立體幾何部分因為抽象化程度較高和對空間想象能力要求較高，更是成為了重要的失分點.GeoGebra作為一款兼具幾何與代數功能的教學輔助軟件，可以實現高中數學教學中所需的幾何圖形的動態變化、代數運算、隨機模擬等功能.本文結合《棱柱、棱錐與棱臺的表面積》的教學，談談如何借助GeoGebra的動態演示功能，幫助學生直觀的感知立體幾何的魅力，構建概念的認知體系.

2 教材的結構與內容安排

本節課是人教版必修第二冊第八章第三節《簡單幾何體的表面積與體積》的第一課時.主要內容是棱柱、棱錐、棱臺的表面積與體積公式及其求法，以及一些簡單組合體的表面積與體積求法.新課標指出立體幾何是研究現實世界中物體的形狀、大小與位置關系的數學學科.立體幾何教學中應運用直觀感知、操作確認、推理論證、度量計算等探索空間圖形的性質，建立空間觀念.

教材將側面展開圖作為簡單幾何體的表面積的切入點，通過分析側面展開圖得到了簡單幾何體的表面積公式，充分體現了立體問題平面化的解題策略，培養了學生直觀想象和數學運算的核心素養.在簡單幾何體的體積教學的處理上，教材采取從特殊到一般的探究路徑，從學生最熟悉的正方體與長方體的體積入手，得到了棱柱的體積公式，又通過棱柱、棱錐與棱臺的關系進一步拓展延伸得到了棱錐與棱臺的體積公式.采用由淺入深、由易到難的探究路徑，按照直觀感知—操作確認—推理論證—度量計算的邏輯展開，培養了學生邏輯推理和數學抽象的核心素養.

3 教學問題診斷

1.本節課教學的重點是棱柱、棱錐、棱臺的表面積及體積公式的推導，盡管在之前的學習中學生已經掌握了棱柱、棱錐以及棱臺的結構特征，又從研究空間點、線、面之間的關系中掌握了“降維”與“轉化”的思想方法，但是空間想象能力的不足和參差都將是學生學習本節課的阻礙.

2.以往的教學中，要么是教師直接灌輸公式，要么是用幾何畫板來制作相對繁瑣的課件，但在本節課中，借助Geogebra的3D功能只需要走幾個指令就可以完成動畫，并實現棱柱、棱錐和棱臺的轉換，直觀的探究三者的關系，真正體會數與形的和諧統一.

4 教學策略

本節課主要分為兩個模塊，一是棱柱、棱錐、棱臺的表面積的計算、公式的探究以及應用.二是棱柱、棱錐、棱臺的體積計算、公式的探究以及應用.教學方法上，以學生的自主探究為主，教師借助信息技術進行直觀演示，對學生的探究過程及思路進行引導和補充.

5 教學過程

5.1 以舊拓新，引發懸念

用快遞包裝視頻，創設問題情境，引導學生回憶表面積和展開圖的定義，提出問題1.

問題1：在初中，我們已經學習過正方體和長方體的表面積和展開圖，它們之間的關系是什么？

教師利用Geogebra展示正方體的展開圖.引導學生發現正方體的展開圖面積就是正方體的表面積.

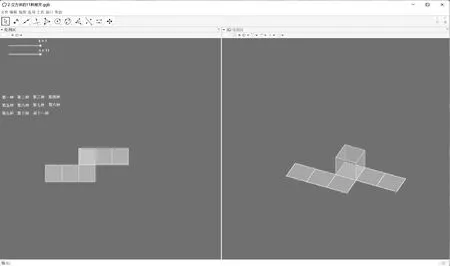
探究：棱柱、棱錐、棱臺都是由多個平面圖形圍成的幾何體，他們的平面展開圖是什么？他們的表面積又應該如何計算呢？

設計意圖：數學來源于生活，也將服務于生活.表面積的求解不是憑空產生的，而是為了解決實際需要而誕生的.讓學生明白為什么學？引導學生通過復習回顧，發現展開圖與表面積的關系，感受“空間問題平面化”的解題思維.

5.2 3D大片，凝聚精華

我們首先來研究一些特殊的多面體，側棱和底面垂直的棱柱叫做直棱柱，特別的，底面為正多邊形的直棱柱叫做正棱柱.

問題2：正棱柱的側面展開圖是什么樣的？它的表面積應該如何求解？

教師用Geogebra演示正三棱柱的展開變化過程，發現正三棱柱的側面展開圖是矩形.

追問1：那么對于其他的正棱柱，他們的側面展開圖也是矩形嗎？

追問2：直三棱柱的側面展開圖是什么形狀，如何求解？

教師用Geogebra演示當邊數變化時其他正棱柱的側面展開圖.發現正棱柱的側面展開圖均為矩形.矩形的長等于正棱柱底面周長c，矩形的寬等于正棱柱的高h.學生很容易得出直棱柱的側面積S側=ch.

師：如果一個棱錐的底面是正多邊形，并且頂點在底面的正投影是底面中心，那么這樣的棱錐稱為正棱錐.那么正棱錐的表面積如何求解？

問題3：正棱錐的側面展開圖是什么形狀？如何求解它的側面積？

教師借助Geogebra展示正六棱錐的側面展開圖.

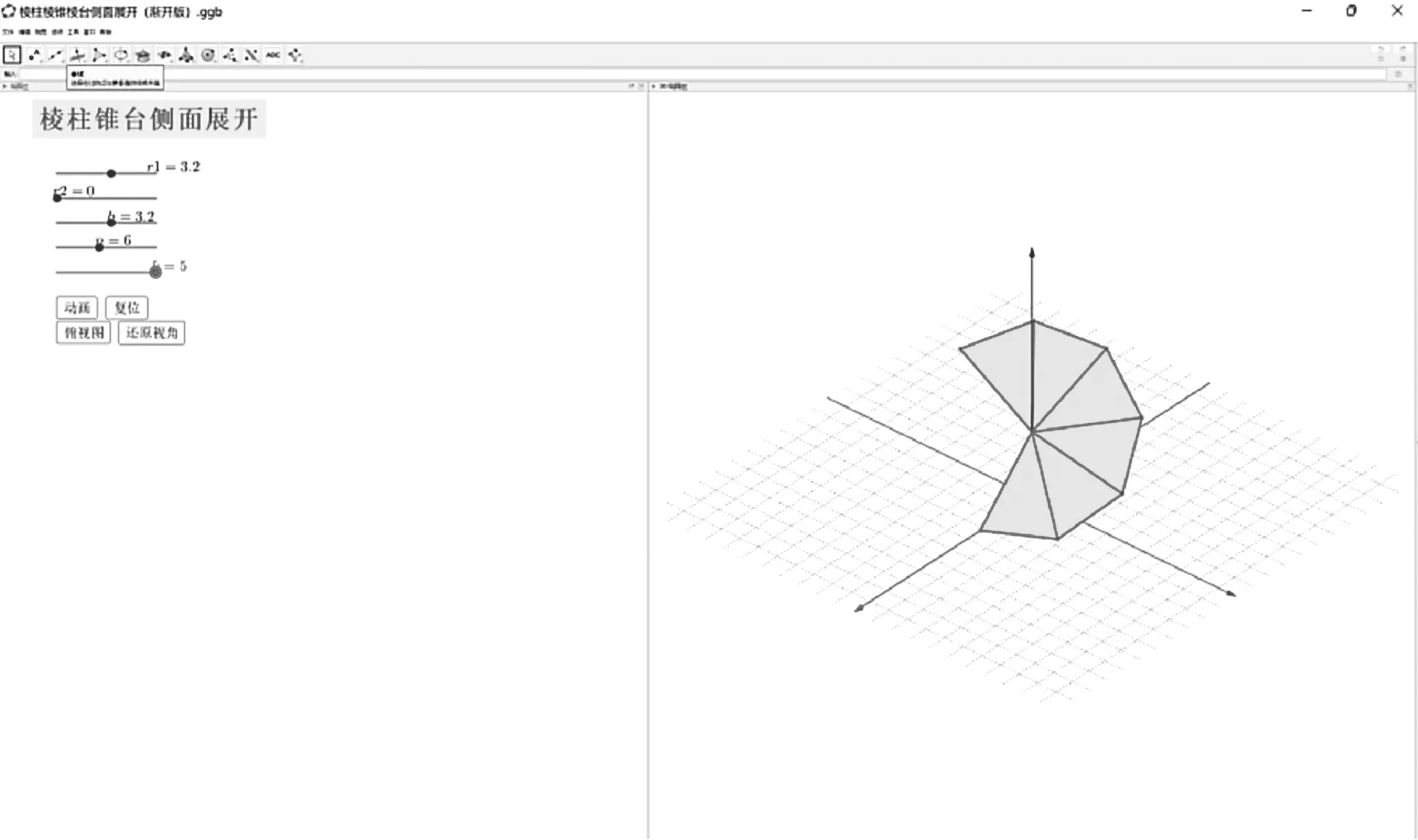
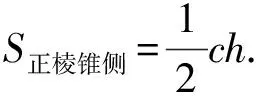
問題4：正棱臺的側面展開圖是什么樣的，如何求解正棱臺的側面積.

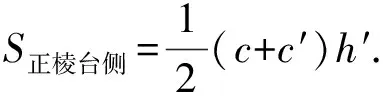
設計意圖：相比于棱錐、棱臺，由于初中對長方體和正方體的研究，學生對于棱柱更為了解，接受起來也更加容易.再者，棱錐和棱臺也可以由棱柱轉化而來.學生在研究棱柱表面積的基礎上，所以借助直觀感受對棱錐和棱臺進行合作探究以及自主探究，進一步應用降維和轉化這兩個研究立體幾何的思維方法.

5.3 小試牛刀，學以致用

例1已知如圖，四面體S-ABC的棱長均為a，求它的表面積.

例2已知一個正四棱錐P-ABCD的側棱長為5，底面的邊長為6，求它的表面積.

設計意圖：通過兩道題讓學生明白求解棱柱、棱錐、棱臺的側面積的問題就可轉化為求平行四邊形、三角形、梯形的面積問題.在探究棱柱，棱錐，棱臺的基礎上，形成從空間問題到平面問題轉化的思路，掌握求解表面積問題的一般方法.

5.4 總結歸納，有始有終

問題5：本節課我們學習了什么知識？在探究過程中我們應用了哪些數學思想？你能夠從今天學習的知識中發現棱柱、棱錐與棱臺之間的關系嗎？

教師用Geogebra演示棱柱、棱錐與棱臺的轉化過程.學生通過直觀感知，借助公式進行總結.在學生進行總結之后，教師借助Geogebra進行動畫演示，加強學生對于公式的理解，同時為下節課棱柱、棱錐以及棱臺的體積的探究進行鋪墊.

6 教學反思

本節課的教學設計采用直觀想象、操作確認的方式展開，借助類比歸納的思維方法,在GeoGebra的輔助下通過動態呈現側面展開的過程，增強學生對展開圖的面積即側面積的認識，培養直觀想象的核心素養，進一步感受“空間問題平面化”這種降維、轉化的思想方法.利用GeoGebra的3D平臺，通過滑動條的設置，為學生理解和掌握柱體、錐體和臺體的側面積公式的聯系提供了便利，化“無形”為“有形”，從“數”與“形”的多重表征促進學生對知識的深度理解.