結(jié)合密度比和系統(tǒng)演化的密度峰值聚類算法

曹俊茸，張德生，肖燕婷

西安理工大學(xué) 理學(xué)院，西安 710054

聚類分析[1]是一種無(wú)監(jiān)督學(xué)習(xí)，能夠根據(jù)數(shù)據(jù)對(duì)象的特征，對(duì)數(shù)據(jù)進(jìn)行有效分類，被廣泛發(fā)展和應(yīng)用于數(shù)據(jù)挖掘[2]、圖像分割、基因工程[3]等領(lǐng)域。2014 年，意大利學(xué)者Rodriguez和Laio在Science上發(fā)表了一種新的聚類算法——密度峰值聚類算法（clustering by fast search and find of density peaks）[4]，簡(jiǎn)稱DPC算法。該算法輸入?yún)?shù)較少，能夠?qū)Ω鞣N類型的數(shù)據(jù)集進(jìn)行聚類，并且能夠剔除噪聲數(shù)據(jù)的影響，取得較好的聚類效果。自從該算法提出以來，受到了國(guó)內(nèi)外學(xué)者的廣泛關(guān)注，對(duì)其進(jìn)行了多種改進(jìn)，王洋等人[5]采用基尼不純度來度量數(shù)據(jù)勢(shì)能的分布來優(yōu)化截?cái)嗑嚯x的選取，基尼指數(shù)取最小值時(shí)，數(shù)據(jù)的不純度最小，數(shù)據(jù)的勢(shì)能差別最大，更易于聚類，解決了DPC算法無(wú)法處理復(fù)雜數(shù)據(jù)集的缺陷；杜沛等人[6]將K近鄰思想引入密度計(jì)算中，結(jié)合校準(zhǔn)量來選取截?cái)嗑嚯x，對(duì)任意數(shù)據(jù)都能自適應(yīng)選擇截?cái)嗑嚯x，能夠處理密度變化大的數(shù)據(jù)集；文獻(xiàn)[7]定義了下屬的概念來描述相對(duì)密度關(guān)系，并以下屬的數(shù)量作為判斷聚類中心的標(biāo)準(zhǔn)，利用相對(duì)密度關(guān)系，使得算法較少受到密度核和密度差異的影響；文獻(xiàn)[8]提出了一種基于殘差的密度峰值聚類算法，通過殘差計(jì)算測(cè)量局部密度，然后利用產(chǎn)生的殘差生成殘差碎片形成簇，并提出了一種半自動(dòng)聚類識(shí)別方法，消除了人工質(zhì)心選擇的迭代過程；文獻(xiàn)[9]為了提高DPC算法處理低密度節(jié)點(diǎn)的性能，采用Halo 算法，提出了一種改進(jìn)的暈節(jié)點(diǎn)密度峰值聚類算法（HaloDPC），提高了處理不同密度、不規(guī)則形狀的類簇、離群點(diǎn)檢測(cè)的能力；文獻(xiàn)[10]提出了一種新的基于分層方法的聚類算法，即多中心密度峰值聚類（McDPC），假設(shè)潛在的集群中心彼此之間的距離相對(duì)較遠(yuǎn)，并且與其他高密度數(shù)據(jù)點(diǎn)的最小距離相對(duì)較大，將具有代表性的數(shù)據(jù)點(diǎn)自動(dòng)劃分為不同的密度級(jí)別，處理每個(gè)層次上的類簇，以確定多中心簇，解決了DPC算法無(wú)法識(shí)別出具有多個(gè)密度峰值的簇，或無(wú)法識(shí)別局部密度相對(duì)較低簇的問題；文獻(xiàn)[11]針對(duì)DPC算法需要人工確定截?cái)嗑嚯x并圈出聚類中心的缺點(diǎn)，根據(jù)K近鄰獲取樣本點(diǎn)密度，并對(duì)相對(duì)距離進(jìn)行樣本排序，然后找到密度趨勢(shì)的轉(zhuǎn)向位置，并根據(jù)轉(zhuǎn)向位置確定截?cái)嗑嚯x，尋找可能成為聚類中心的數(shù)據(jù)點(diǎn)，比較它們之間的相似性，確定最終的聚類中心；高詩(shī)瑩等人[12]提出了基于密度比例的密度峰值聚類算法（R-CFSFDP），通過計(jì)算一個(gè)點(diǎn)與其周圍點(diǎn)的密度比來提高數(shù)據(jù)中密度較小的數(shù)據(jù)對(duì)象辨識(shí)度，解決了DPC 算法對(duì)密度較小簇的遺漏問題。

通過對(duì)DPC 算法的多種改進(jìn)，使得DPC 算法已經(jīng)成為常用的聚類算法之一，但是，該算法仍然存在一些不足之處：（1）截?cái)嗑嚯x的選取對(duì)局部密度的計(jì)算有直接的影響，進(jìn)而影響聚類中心的選擇。特別地，如果截?cái)嗑嚯x被賦予一個(gè)很大的值，計(jì)算出的密度約為N（數(shù)據(jù)對(duì)象總數(shù)），重疊區(qū)域包括了來自其他類簇的數(shù)據(jù)。相反，如果選擇的截?cái)嗑嚯x太小，計(jì)算出的密度約為零，那么每個(gè)點(diǎn)都有相似的近鄰區(qū)域。在這兩種情況下，所計(jì)算出的局部密度對(duì)判別數(shù)據(jù)類別的價(jià)值較小。（2）DPC算法是根據(jù)決策圖與用戶進(jìn)行互動(dòng)截取聚類中心，這就會(huì)使得不同的人會(huì)分析出不同的結(jié)果，導(dǎo)致聚類結(jié)果的不一致。

針對(duì)以上兩個(gè)問題，本文提出了基于密度比和系統(tǒng)演化的密度峰值聚類算法（DS-DPC）。首先，利用密度比的思想改進(jìn)密度計(jì)算公式，使密度能夠反映周圍數(shù)據(jù)的分布情況；然后，根據(jù)局部密度與相對(duì)距離的乘積排序情況，選出聚類中心，對(duì)剩余樣本進(jìn)行聚類；最后，利用系統(tǒng)演化方法判斷聚類結(jié)果是否需要合并或分離。

1 預(yù)備知識(shí)

1.1 密度峰值聚類算法

密度峰值聚類算法是一種基于密度的聚類方法，它基于下面兩個(gè)假設(shè)：（1）類簇中心的密度大于與其相鄰的非中心點(diǎn)的密度；（2）類簇中心之間通常相距較遠(yuǎn)。通過計(jì)算每個(gè)點(diǎn)的局部密度和相對(duì)距離，繪制以局部密度為橫坐標(biāo)，相對(duì)距離為縱坐標(biāo)的決策圖，根據(jù)決策圖，選取右上角的點(diǎn)為聚類中心，其余的點(diǎn)根據(jù)局部密度就近分配。

對(duì)于每個(gè)數(shù)據(jù)點(diǎn)xi∈X={ }x1,x2,…,xN，首先計(jì)算其局部密度ρi和距離最近較大密度點(diǎn)的相對(duì)距離δi，當(dāng)數(shù)據(jù)是離散數(shù)據(jù)時(shí)，局部密度計(jì)算公式如下：

截?cái)嗑嚯xdc依據(jù)經(jīng)驗(yàn)選取，文獻(xiàn)[4]中給出了dc的選擇方法：使各點(diǎn)的平均鄰居數(shù)約占數(shù)據(jù)對(duì)象總數(shù)的1%到2%，也給出了無(wú)法根據(jù)決策圖判斷聚類中心的情況，利用局部密度與相對(duì)距離的乘積γi的值，γi越大，越可能被選為聚類中心。

此外，DPC 算法給出了判斷核心點(diǎn)和噪聲點(diǎn)的方法，定義了邊界區(qū)域密度：一個(gè)類中的數(shù)據(jù)對(duì)象距其他類的數(shù)據(jù)對(duì)象之間的距離小于截?cái)嗑嚯xdc的所有數(shù)據(jù)對(duì)象的平均密度。局部密度大于邊界區(qū)域密度的數(shù)據(jù)對(duì)象被視為核心數(shù)據(jù)，否則，被視為噪聲數(shù)據(jù)。

1.2 自然最近鄰搜索

經(jīng)典的k-最近鄰和ε-最近鄰都存在參數(shù)的選擇問題。本質(zhì)上，都是檢測(cè)數(shù)據(jù)集附近的鄰域，完全忽略數(shù)據(jù)特征，不能適應(yīng)不同規(guī)模的數(shù)據(jù)集。自然最近鄰[13]是一種新的最近鄰概念，與k-最近鄰和ε-最近鄰相比，自然最近鄰被動(dòng)選擇鄰居，對(duì)于一個(gè)數(shù)據(jù)點(diǎn)xi，只有當(dāng)另一個(gè)點(diǎn)xj以它作為鄰居時(shí)，點(diǎn)xi才能算擁有一個(gè)鄰居，這樣的定義能更好地反映數(shù)據(jù)特征。

定義3（自然最近鄰特征值）當(dāng)搜索達(dá)到穩(wěn)定狀態(tài)時(shí)，自然最近鄰特征值就是搜索次數(shù)r。

由于自然最近鄰特征值很大時(shí)，會(huì)大大增加算法的時(shí)間復(fù)雜度，文獻(xiàn)[14]對(duì)自然最近鄰算法進(jìn)行了優(yōu)化：隨著r值的增加，如果鄰居數(shù)目為0的數(shù)據(jù)對(duì)象個(gè)數(shù)不再發(fā)生變化，就停止搜索。

2 本文算法

本文主要對(duì)密度峰值聚類算法進(jìn)行如下兩個(gè)方面的改進(jìn)：（1）重新定義局部密度公式；（2）利用系統(tǒng)演化方法判斷兩個(gè)類簇是否需要合并或分離。

2.1 改進(jìn)的局部密度

運(yùn)用自然最近鄰搜索方法找到每個(gè)數(shù)據(jù)點(diǎn)的自然最近鄰個(gè)數(shù)，為了使低密度區(qū)域的簇不被DPC 算法歸為噪聲，高密度的簇邊界區(qū)域中沒有點(diǎn)被識(shí)別為聚類中心，需要用一個(gè)相對(duì)的密度來替換原來的密度度量。運(yùn)用密度比的思想，一個(gè)數(shù)據(jù)點(diǎn)的密度不僅要度量其截?cái)嗑嚯x領(lǐng)域內(nèi)的密度，還需要再選取一個(gè)更大的截?cái)嗑嚯x，計(jì)算這兩個(gè)領(lǐng)域的密度比來衡量一個(gè)點(diǎn)的密度。通過這樣做，能夠處理簇間密度的變化。但是，密度比公式的計(jì)算中需要輸入兩個(gè)截?cái)嗑嚯x參數(shù)，不能自動(dòng)獲取參數(shù)，因此，本文結(jié)合自然最近鄰搜索，將密度公式改進(jìn)為：

其中，nb(i)是自然最近鄰搜索中當(dāng)鄰居個(gè)數(shù)為0 的點(diǎn)不再變化時(shí)停止搜索，數(shù)據(jù)點(diǎn)xi的最近鄰個(gè)數(shù)，而nk(i)則是當(dāng)自然最近鄰搜索達(dá)到穩(wěn)定狀態(tài)時(shí)，數(shù)據(jù)點(diǎn)xi的最近鄰個(gè)數(shù)。

2.2 判斷類簇是否需要合并

DPC 算法給出了γi值的定義，本文運(yùn)用γi的排序值挑選出前N（N是數(shù)據(jù)點(diǎn)個(gè)數(shù)）個(gè)數(shù)據(jù)點(diǎn)作為聚類中心，將剩余數(shù)據(jù)點(diǎn)就近分配到密度更高的類簇中。再利用文獻(xiàn)[15]的系統(tǒng)演化方法對(duì)聚類結(jié)果進(jìn)行合并或分離，具體定義如下。

如圖1 所示，假設(shè)有兩個(gè)類簇，簇A 和簇B，每個(gè)簇被分割成m個(gè)區(qū)域。設(shè)簇A和簇B之間距離最近的兩個(gè)區(qū)域?yàn)檫吔鐓^(qū)域A1和B1，設(shè)A2為簇A的中心區(qū)域，B2為簇B的中心區(qū)域。

（1）將簇分為不同的區(qū)域。

設(shè)N1和N2分別為簇A和簇B數(shù)據(jù)對(duì)象的總數(shù)，則將簇A分為m1個(gè)區(qū)域，簇B分為m2個(gè)區(qū)域。

（2）找邊界區(qū)域A1、B1：從簇A 中選擇n1個(gè)距簇B最近的數(shù)據(jù)對(duì)象組成A1區(qū)域，從簇B中選擇n2個(gè)距簇A最近的數(shù)據(jù)對(duì)象組成B1區(qū)域。

（3）找中心區(qū)域A2、B2，從簇A中找出離A1最近的n1個(gè)數(shù)據(jù)對(duì)象，形成A2 區(qū)域，類似地，從簇B 中找到n2個(gè)數(shù)據(jù)對(duì)象形成B2區(qū)域。

（4）找出A1和B1的交叉區(qū)域F，從A1和B1中各找出一半離彼此近的數(shù)據(jù)對(duì)象，組成交叉區(qū)域F。

（5）簇A與簇B之間的邊界距離DAB為：

測(cè)量A1 中的平均距離DA1為A1 中各對(duì)象間的平均步長(zhǎng)距離，其中A1 的步長(zhǎng)是：從A1 中的兩個(gè)相距最遠(yuǎn)的數(shù)據(jù)點(diǎn)h1（或hk）出發(fā)，找到下一個(gè)距離h1最近的對(duì)象h2（計(jì)算h1與除h1之外的所有對(duì)象的距離，并選擇距離最小的對(duì)象），計(jì)算它們之間的距離，類似地，繼續(xù)通過h2找到下一個(gè)最近的對(duì)象直到到達(dá)hk。

同樣，DA2、DB1、DB2、DA1A2、DB1B2、DA1B1、DF分別是A2、B1、B2、A1A2、B1B2、A1B1、F區(qū)域的平均距離。

當(dāng)數(shù)據(jù)對(duì)象有如圖2 所示的情況時(shí)，左邊數(shù)據(jù)點(diǎn)1到中間兩個(gè)點(diǎn)（點(diǎn)2和點(diǎn)3）的距離相等，選擇點(diǎn)2或點(diǎn)3其中一個(gè)作為下一個(gè)點(diǎn)會(huì)計(jì)算出不同的平均距離，因此本文將平均距離的計(jì)算改進(jìn)為計(jì)算所有數(shù)據(jù)對(duì)象的平均距離。即：

系統(tǒng)演化方法推導(dǎo)出的可分性信息為：（1）當(dāng)Dn ＞0 時(shí)，兩個(gè)類簇完全可以分離；

（2）當(dāng)Dn≤0 且Ep ＞Em時(shí)，兩個(gè)類簇有輕微重合；

（3）當(dāng)Dn≤0 且Ep≤Em時(shí)，兩個(gè)類簇可以聚合在一起。

對(duì)于系統(tǒng)演化方法不能分辨兩個(gè)類簇有輕微重合時(shí)的情況，則計(jì)算兩個(gè)類簇的自然近鄰數(shù)目，如果合并兩個(gè)簇后，每個(gè)數(shù)據(jù)點(diǎn)的平均自然近鄰數(shù)目增加，則將兩個(gè)簇合并，否則，不合并兩個(gè)簇。

2.3 DS-DPC算法描述

本文算法主要是在DPC 算法的基礎(chǔ)上，計(jì)算局部密度時(shí)，運(yùn)用密度比的思想以避免噪聲點(diǎn)具有較高的密度，或者高密度的簇邊界區(qū)域中的點(diǎn)被識(shí)別為聚類中心，其次，引入了系統(tǒng)演化方法對(duì)聚類后的結(jié)果進(jìn)行判斷，進(jìn)一步得到聚類結(jié)果。

本文算法的基本步驟如下，算法流程如圖3。

輸入：數(shù)據(jù)集X={x1,x2,…,xN}，數(shù)據(jù)點(diǎn)個(gè)數(shù)為N。

輸出：聚類結(jié)果C={c1,c2,…,ck} ，類簇個(gè)數(shù)為k。

步驟1 根據(jù)自然最近鄰搜索找出每個(gè)點(diǎn)xi的自然最近鄰。

步驟2 分別根據(jù)公式（9）和公式（4）計(jì)算每個(gè)點(diǎn)的局部密度ρi和相對(duì)距離δi。

步驟3 計(jì)算局部密度和相對(duì)距離的乘積γi，并對(duì)其進(jìn)行排序。

步驟4 選取γi排序中前N個(gè)點(diǎn)作為聚類中心，并將剩余點(diǎn)就近分配到密度更高的簇中。

步驟5 根據(jù)類簇中心之間的距離，對(duì)N個(gè)類簇就近進(jìn)行兩兩配對(duì)，利用系統(tǒng)演化方法判斷每對(duì)類簇是否需要合并。

步驟6 將上一步得到的聚類結(jié)果再次進(jìn)行兩兩配對(duì)，利用系統(tǒng)演化方法判斷是否需要合并。

步驟7 判斷所得結(jié)果中每對(duì)類簇是否處于分離狀態(tài)，若是，則算法結(jié)束，得到最終聚類結(jié)果。若否，則轉(zhuǎn)至步驟6繼續(xù)判斷類簇的合并與分離。

2.4 算法時(shí)間復(fù)雜度分析

對(duì)于一個(gè)含有N個(gè)樣本的數(shù)據(jù)集，設(shè)c為N2，本文所提算法的時(shí)間復(fù)雜度主要來源于以下四個(gè)方面：（1）計(jì)算距離矩陣，時(shí)間復(fù)雜度為O(N2)；（2）用自然最近鄰搜索一個(gè)點(diǎn)的第r個(gè)最近鄰，時(shí)間復(fù)雜度為O(lbN)，λ為自然最近鄰搜索達(dá)到穩(wěn)定狀態(tài)時(shí)的搜索次數(shù)，因此，搜索所有點(diǎn)的自然最近鄰的時(shí)間復(fù)雜度為O(λ·N·lbN)；（3）相對(duì)距離計(jì)算的時(shí)間復(fù)雜度為O(N2)；（4）利用系統(tǒng)演化方法判斷分別含有N1和N2個(gè)樣本的兩個(gè)類簇是否可以合并的時(shí)間復(fù)雜度為O(N21)+O(N22)，因此，系統(tǒng)演化方法總的時(shí)間復(fù)雜度為O(c·N21)+O(c·N22)。綜上，本文所提算法的時(shí)間復(fù)雜度約為O(c·N2)。

3 仿真實(shí)驗(yàn)與結(jié)果分析

本文使用MATLAB 進(jìn)行實(shí)驗(yàn)，在三個(gè)人工合成數(shù)據(jù)集和六個(gè)UCI 數(shù)據(jù)集上實(shí)現(xiàn)本文算法，并與常用聚類算法DPC、DBSCAN、K-means 以及CDPC-KNN[6]和CFSFDP-HD[16]算法進(jìn)行比較。表1 和表2 分別是實(shí)驗(yàn)所用人工合成數(shù)據(jù)集和UCI數(shù)據(jù)集的基本信息。

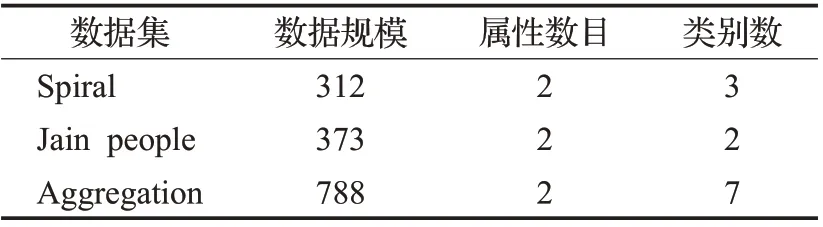
表1 三個(gè)人工合成數(shù)據(jù)集Table 1 Three synthetic datasets

表2 六個(gè)UCI數(shù)據(jù)集Table 2 Six UCI datasets

3.1 聚類評(píng)價(jià)指標(biāo)

本文選用Accuracy 指標(biāo)（ACC）、FMI 指數(shù)、調(diào)整互信息（AMI）以及調(diào)整蘭德系數(shù)（ARI）四個(gè)指標(biāo)評(píng)價(jià)聚類結(jié)果。將本文算法與其他五種聚類算法進(jìn)行比較。

（1）Accuracy指標(biāo)（ACC）

Accuracy 指標(biāo)度量聚類結(jié)果中正確聚類的個(gè)數(shù)占總個(gè)數(shù)的比例，計(jì)算公式為：

其中yi為第i個(gè)類簇中正確聚類的樣本數(shù)目，k為真實(shí)類簇的個(gè)數(shù)，N為數(shù)據(jù)集中樣本的總數(shù)目。ACC 的取值范圍在[0，1]，取值越大，說明聚類結(jié)果與真實(shí)結(jié)果越接近，聚類效果越好。

（2）FMI指數(shù)

FMI指數(shù)是對(duì)精度和召回率的幾何平均，公式如下：

聚類結(jié)果所形成的簇集合為C，樣本的真實(shí)簇集合為D，從數(shù)據(jù)集中任取兩個(gè)樣本，a表示在C和D中都屬于相同簇的樣本對(duì)的數(shù)量。b表示在C中屬于相同簇，而在D中屬于不同簇的樣本對(duì)的數(shù)量。c表示在C中屬于不同簇，而在D中屬于相同簇的樣本對(duì)的數(shù)量。顯然，F(xiàn)MI的取值是在[0，1]，值越大說明聚類效果越好。

（3）調(diào)整互信息（AMI）

AMI公式如下：

AMI 是基于預(yù)測(cè)簇向量與真實(shí)簇向量的互信息分?jǐn)?shù)來衡量其相似度的，AMI 取值范圍在[-1，1]，AMI 越大，說明聚類結(jié)果和真實(shí)結(jié)果的相似度越高，聚類效果越好。

ARI 的取值范圍在[-1，1]，值越大意味著聚類結(jié)果與真實(shí)情況越吻合，主要是用來衡量?jī)蓚€(gè)數(shù)據(jù)分布的吻合程度。

3.2 人工合成數(shù)據(jù)集上的實(shí)驗(yàn)結(jié)果及分析

本文對(duì)比了三個(gè)人工合成數(shù)據(jù)集檢驗(yàn)DS-DPC 算法與其他五種聚類算法的聚類結(jié)果，圖4、圖5、圖6分別是六種算法在Spiral、Jain people 和Aggregation 三個(gè)數(shù)據(jù)集上的聚類效果圖。

對(duì)于Spiral數(shù)據(jù)集，由圖4可以看出，由于對(duì)局部密度公式的改進(jìn)，以及聚類結(jié)果的優(yōu)化，DS-DPC 算法正確識(shí)別出了聚類個(gè)數(shù)，準(zhǔn)確地對(duì)每個(gè)點(diǎn)進(jìn)行了聚類，DPC算法和DBSCAN算法也識(shí)別出了三個(gè)類，K-means算法將聚類中心均勻地分布在數(shù)據(jù)空間中，將聚類中心周圍的點(diǎn)聚為一類，得到的聚類效果較差。K-means算法不適合于發(fā)現(xiàn)非凸面形狀的簇或大小差別很大的簇，因此對(duì)該數(shù)據(jù)集沒有達(dá)到較好的聚類效果。CDPCKNN 算法也能正確地將每個(gè)點(diǎn)進(jìn)行聚類，而CFSFDPHD 算法將一個(gè)類中的一部分分配到了相鄰的一個(gè)類中，聚類效果不佳。

對(duì)于Jain people數(shù)據(jù)集，由圖5可以看出，DS-DPC算法和DPC 算法雖然都能正確識(shí)別聚類個(gè)數(shù)，但DSDPC能更準(zhǔn)確地將兩個(gè)類相交處的點(diǎn)歸類，從圖中還可以看出，DS-DPC算法比DPC算法識(shí)別出的聚類效果更加準(zhǔn)確，DPC 算法只是就近分配，將密度高的點(diǎn)周圍的對(duì)象都分配到了一類，但是沒有分辨出密度分布不一致的兩個(gè)類。對(duì)K-means算法輸入了正確的聚類個(gè)數(shù)，卻將一個(gè)真實(shí)簇的一部分歸類到另一類中，聚類效果最差。CDPC-KNN算法是對(duì)DPC算法的密度和相對(duì)距離的計(jì)算公式進(jìn)行了改進(jìn)，使得決策圖中可以明顯分辨出聚類中心，對(duì)于該數(shù)據(jù)集的聚類效果也很好，CFSFDPHD 算法聚類過程不是自適應(yīng)的，將密度較大的一個(gè)類簇分成了兩部分，聚類結(jié)果出現(xiàn)了錯(cuò)誤。

對(duì)于Aggregation數(shù)據(jù)集，由圖6可以看出，DS-DPC算法和DPC 算法都能準(zhǔn)確對(duì)其進(jìn)行聚類，而DBSCAN算法將周圍一些點(diǎn)識(shí)別為噪聲數(shù)據(jù)，導(dǎo)致聚類結(jié)果不理想，由于K-means 算法只適合于對(duì)球形數(shù)據(jù)聚類，即使輸入了正確的聚類數(shù)目，也未能得出準(zhǔn)確的聚類結(jié)果。Aggregation 數(shù)據(jù)集有七個(gè)類，CDPC-KNN 算法對(duì)該數(shù)據(jù)集的聚類效果中，有少量數(shù)據(jù)沒有正確分類，CFSFDP-HD算法對(duì)該數(shù)據(jù)集的聚類效果較好。

3.3 UCI數(shù)據(jù)集上的實(shí)驗(yàn)結(jié)果及分析

為了觀察在UCI數(shù)據(jù)集上的聚類效果，本文對(duì)選取的六組數(shù)據(jù)集進(jìn)行了六種聚類，并將聚類結(jié)果的評(píng)價(jià)指標(biāo)統(tǒng)計(jì)在表3中。

表3給出了DS-DPC算法與其他五種算法在UCI數(shù)據(jù)集上的評(píng)價(jià)指標(biāo)值的對(duì)比，從表中可以看出，由于對(duì)密度和聚類結(jié)果進(jìn)一步的改進(jìn)，DS-DPC算法的各項(xiàng)評(píng)價(jià)指標(biāo)幾乎都優(yōu)于其他算法。在Iris數(shù)據(jù)集上，DS-DPC算法的四項(xiàng)指標(biāo)都接近于1，表明聚類效果較好。對(duì)于Segmentation 和Dermatology 兩個(gè)較高維數(shù)的數(shù)據(jù)集，DS-DPC算法的聚類效果也較好，而其他五種算法對(duì)這兩個(gè)數(shù)據(jù)集的聚類效果都差一些，尤其是DBSCAN 算法和K-means算法。CDPC-KNN算法對(duì)Wine數(shù)據(jù)集的準(zhǔn)確率也較高，與DS-DPC 算法具有相同的準(zhǔn)確率，并且CDPC-KNN 算法在Ecoil 數(shù)據(jù)集上的聚類評(píng)價(jià)指標(biāo)值都較高。從總體上看，本文算法在高維和低維數(shù)據(jù)集上都取得了較好的聚類效果。

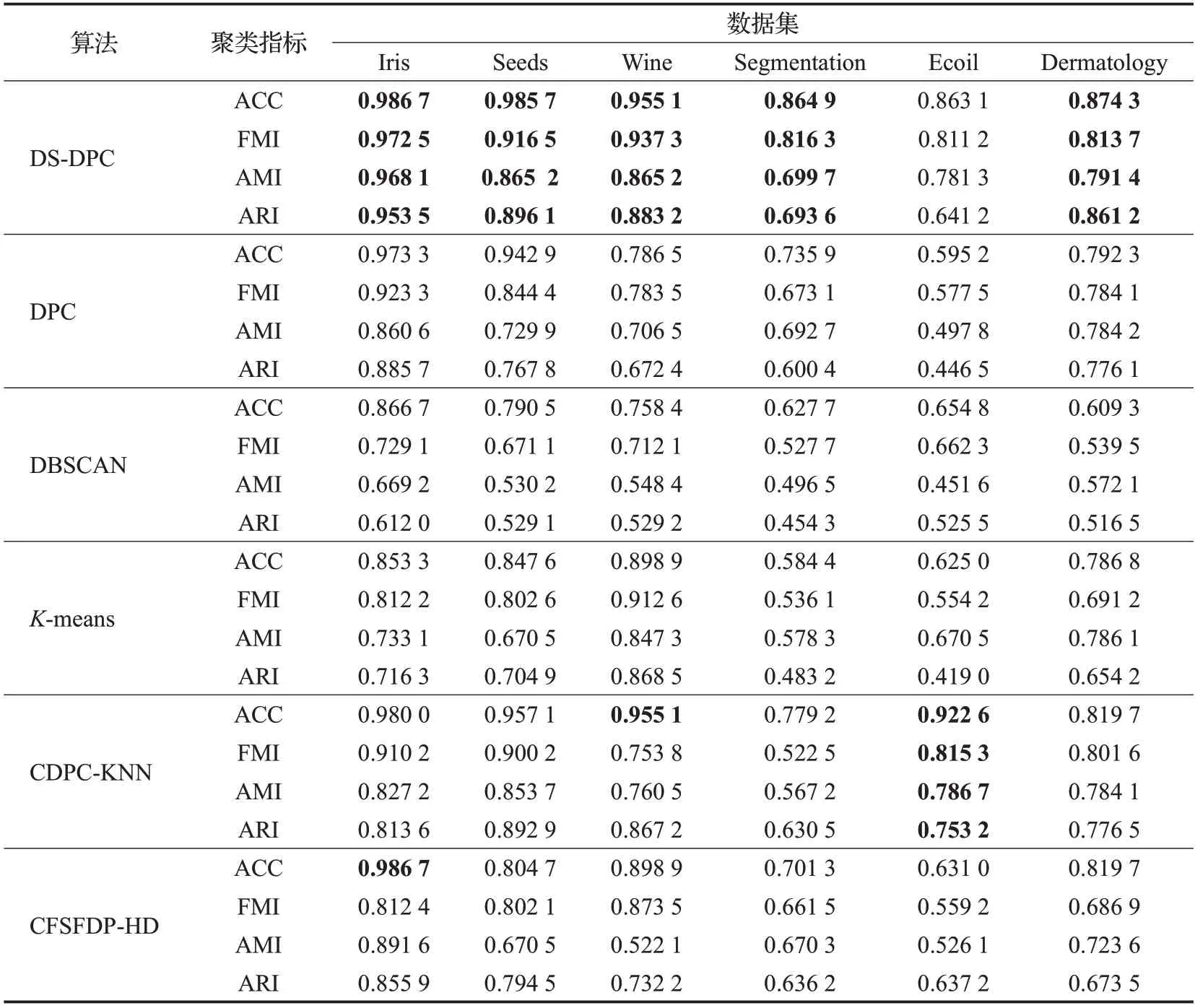
表3 6種算法在UCI數(shù)據(jù)集上的指標(biāo)值Table 3 Index values of six algorithms on UCI dataset

4 結(jié)束語(yǔ)

DPC 算法能夠檢測(cè)任意形狀的簇，易于實(shí)現(xiàn)，但該算法需要輸入?yún)?shù)，并且需要手動(dòng)選擇聚類中心。針對(duì)這些不足，本文提出了一種基于密度比和系統(tǒng)演化的密度峰值聚類算法，對(duì)DPC 算法進(jìn)行了兩個(gè)方面的改進(jìn)。具體的改進(jìn)為：（1）利用自然最近鄰搜索找出每個(gè)點(diǎn)的最近鄰個(gè)數(shù)，并且結(jié)合密度比的思想來計(jì)算樣本的局部密度，使計(jì)算出的密度不僅能夠考慮周圍點(diǎn)的個(gè)數(shù)，也能夠反映出周圍點(diǎn)的分布情況，消除了DPC 算法由于輸入?yún)?shù)而導(dǎo)致的聚類結(jié)果不一致的情況。（2）計(jì)算局部密度與相對(duì)距離的乘積γi，選取γi值較大的點(diǎn)為聚類中心，按照DPC 算法的分配策略進(jìn)行聚類，引入系統(tǒng)演化方法對(duì)DPC 算法的聚類結(jié)果進(jìn)行進(jìn)一步的分析，運(yùn)用公式判斷類簇的合并與分離，避免了手動(dòng)選取聚類中心的主觀性，提高了算法的聚類性能。

通過在人工合成數(shù)據(jù)集和UCI 數(shù)據(jù)集上進(jìn)行實(shí)驗(yàn)驗(yàn)證，結(jié)果表明，本文算法具有一定的優(yōu)越性，下一步的研究應(yīng)該重點(diǎn)討論算法的時(shí)間復(fù)雜度，使DPC 算法能夠適應(yīng)更大規(guī)模數(shù)據(jù)的聚類分析。