移動邊緣計算中的協同計算卸載策略

李 順，葛海波，劉林歡，陳旭濤

西安郵電大學 電子工程學院，西安 710121

隨著網絡時代的來臨，網絡設備的使用量呈爆發式增長。人們在移動設備上執行任務時對數據速率和服務質量的要求越來越高，卸載任務的類型也越來越復雜，如增強現實（augmented reality，AR）、手勢識別、人臉識別等[1]，這些應用不僅是計算任務密集型，而且對時延要求敏感。隨著技術的發展，盡管現在移動設備的中央處理器（CPU）速率已經得到很大的提升，但在需要大量計算資源的應用面前在短時間內也是無能為力。移動云計算（mobile cloud computing，MCC）中將計算資源需求量大的任務卸載至遠端具有強大計算能力的云服務器中，能夠在保證時延和能耗的前提下高效的解決這一問題。由于云服務器與用戶之間距離較遠，在傳輸過程中由于各種因素的影響導致高時延問題，為了解決這一問題，業內學者將目光聚焦到移動邊緣計算（mobile edge computing，MEC）上來[2]，MEC 將遠端服務器的計算和存儲資源遷下沉到用戶端，降低計算任務傳輸時延和能量消耗，并且對計算資源需求量很大的任務，直接將其傳輸到遠端計算能力更強的云服務器中執行。MEC 靠近用戶端設備但計算能力有限，MCC 遠離用戶端設備但其計算能力巨大，兩者相互協作能夠滿足不同的應用場景。

計算卸載作為MEC 的主要優勢之一，成為廣大研究人員的關注熱點[3]。在現有的移動邊緣計算任務卸載的研究中，用戶將任務卸載至邊緣服務器或者云服務器，忽略了附近擁有計算資源的邊緣服務器，導致這部分計算資源的浪費。將任務卸載至邊緣服務器時，邊緣服務器之間作為一個協同的整體對卸載的任務進行計算，能夠有效減少向遠程云傳輸的時間成本。

本文中結合MCC和MEC的優勢，將邊緣服務器及其附近邊緣服務器看作一個協同整體，任務選擇卸載至本地、本地邊緣服務器、附近邊緣服務器中以及云服務器中計算。將任務卸載中傳輸時延與能耗建立模型，并分別賦予權重值，通過改進的混合粒子群算法找到最優解，并得到最優的卸載策略。

1 相關工作

隨著5G的迅速發展以及普及，MEC的發展和研究迎來了新的高度。在MEC 的研究中，計算卸載技術一直備受關注，大量的學者也對其進行了研究并有了突破性的進展[4]。文獻[5]提出一種無線感知聯合調度和計算卸載的策略（joint scheduling and compute offloading，JSCO），通過在移動端和云端并行處理的方式，減少了執行時間，并將優先關系和總執行時間作為約束條件，以此來權衡能耗。文獻[6]研究了具有小型網絡的MEC系統節能計算卸載策略，通過聯合優化功率、無線和計算資源分配等因素最小化終端能耗，將卸載問題表述為NP-hard的MINLP問題，提出了一種基于遺傳和粒子群（hierarchical genetic algorithm and particle swarm optimization based computation algorithm，HGPCA）的計算卸載策略。但在文中重點考慮了能耗問題，時延問題有所忽略。文獻[7]提出一種基于粒子群優化的卸載策略，將任務卸載表示為能耗約束下的時延最小化問題，并通過懲罰函數平衡時延和能耗。文章中只考慮了時延敏感型的應用，對于能耗方面的關注不足。文獻[8]研究了協同計算卸載、計算和通信資源分配方案，開發了一個協同計算框架，考慮了卸載策略、計算資源等因素提出一種基于管道的策略，并采用經典的逐次凸逼近（successive convex approximation，SCA）方法將非凸優化問題轉化為凸優化問題。文獻[9]針對網絡節點的計算能力與現實通信資源之間的差異，根據距離的遠近以及網絡節點密度的疏密，提出基于遺傳算法的近岸多節點協同卸載策略和遠岸基于分組交叉粒子群可容錯卸載策略。文獻[10]考慮了延遲、內存、可用能量以及智能設備的傳輸能量等約束，通過非線性約束優化問題，提出一種元啟發式算法的部分計算卸載策略。文獻[11]實現復雜依賴應用的低能量遷移問題，在子任務關系的基礎上構建能量最小化的劃分模型，并從任務遷移、執行位置和電量剩余三個方面出發提出一種基于遺傳算法（fine-grainedtask migration energy-saving strategy based on genetic algorithm，FGMBGA）的卸載策略，通過調整任務能耗和手機電量來動態調整最優解。文獻[12]為了使用戶獨立選擇卸載決策，提出一種基于博弈論的分散計算卸載算法，并且在卸載過程中將問題轉化為部分觀測型的馬爾可夫決策過程（partially observed markov decision processes，POMDP），并通過基于策略梯度深度強化學習（deep reinforcement learning，DRL）來解決此問題。文獻[13]研究了在云邊協作系統中，將通信和計算資源共同分配問題轉化為凸優化問題，最終得到資源分配策略。能夠看出文獻所提策略有效減少設備的時延，但對能耗問題關注度相對較少。綜合上述文獻研究總結對比如表1所示。

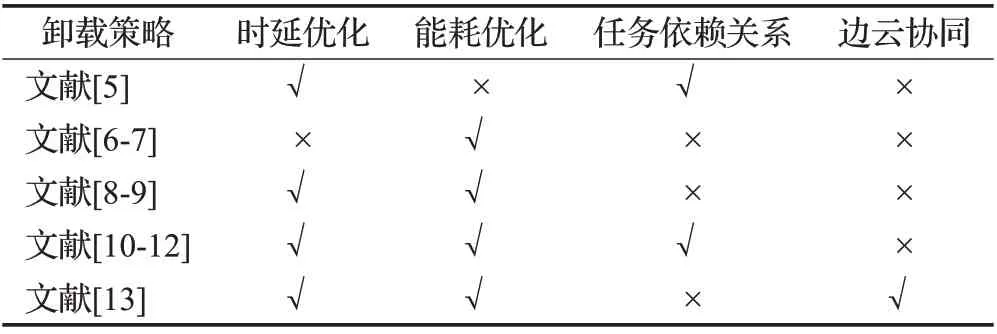
表1 不同卸載策略總結對比Table 1 Comparison of different uninstall strategies

綜上所述，以上計算卸載策略問題的研究，大多只對時延或能耗進行優化，亦或對任務之間的依賴關系沒有考慮。另外，大部分工作只針對移動邊緣計算或者移動云計算的卸載策略進行研究，并沒有考慮MEC 與MCC 之間的協同。綜合考慮上述研究的局限性，本文設計了一種云邊協同的計算卸載策略，并提出了CRPSO計算卸載算法。主要工作如下：

（1）為防止任務無序執行時導致服務器負載過高，無法很好地執行卸載策略，很大程度上影響卸載進度，考慮了任務之間的依賴關系，并使用任務的優先級矩陣表示任務執行的先后順序，優化卸載效率。

（2）在任務卸載時，利用MCC 和MEC 各自的傳輸時延和計算能力特點，將任務采用就近原則卸載，總體考慮移動設備、邊緣服務器和云服務器的計算資源，將計算任務卸載至附近有計算資源的邊緣服務器中，形成邊緣服務器間的協同卸載，合理利用本地端、邊緣端和云端服務器的計算資源。

（3）設計了基于改進混合粒子群算法的計算卸載算法，利用改進后的算法對粒子進行分組交叉迭代后得到最優卸載策略，從而得到最小系統總代價。

2 系統模型

2.1 通信模型

本文提出的移動云計算融合MEC的網絡通信框架模型如圖1 所示，分為三層：用戶層、邊緣計算層、云計算層。其中，云計算層有高性能的服務器群組成，具有強大的計算能力并且能夠協同管理邊緣層服務器之間的資源；邊緣計算層由小型基站以及具有一般計算能和存儲能力的邊緣服務器組成；用戶層可根據自身設備計算和存儲能力計算一定范圍內的任務。

2.2 計算卸載模型

假設用戶在進行任務卸載時的卸載決策：

本地執行：計算任務在本地用戶設備執行。

邊緣服務器執行：通過無線網絡將計算任務卸載至邊緣服務器或者周邊具有計算能力的邊緣服務器執行。

云服務器執行：云服務器具有強大的計算能力。

假設由n個任務T={ }T1,T2,…,Tn。其中每個任務被建模為一個三元組{ }αi,βi,γi，其中，αi表示任務Ti的輸入數據量，βi表示任務計算的數據量，γi表示為反饋計算任務結果的數據量。移動設備、邊緣端和云端服務器的計算力（單位：GHz）分別為fl、fe、fc；移動設備、邊緣服務器和云服務器計算1 bit 數據所需CPU 周期分別為Clb、Ceb、Ccb。其中本地與異地邊緣服務器計算能力相同。

在任務執行的過程中，移動服務中往往不只存在一個任務，任務與任務之間存在依賴關系，所以在任務卸載時要考慮任務卸載的優先關系。引入n×n的任務卸載優先級矩陣D來表示任務i與任務j的優先關系：

由于用戶產生的任務數量的不固定性，任務之間的關系也是不確定的，由此可以根據具體數量和關系自定義矩陣，如圖2 所示為3.2 節中7 個任務的優先級矩陣。例如，D23=1，則說明任務2優于任務3先執行；D26=0，說明任務2 與任務6 之間無約束關系；D56=-1，說明任務6優于任務5先執行。

（2）卸載至邊緣服務器執行

將任務卸載至邊緣服務器時，邊緣服務器可以看作一個感知節點，若邊緣服務器過載，則可以將任務卸載至附近資源較多的邊緣服務器進行計算，然后將結果回傳給用戶端。根據Shannon公式，移動用戶與邊緣服務器的通信傳輸速率為：其中，l2為本地邊緣服務器與異地邊緣服務器之間的距離。

任務i從本地邊緣服務器卸載至異地邊緣服務器執行時，時間延遲為：其中，l3為用戶設備與云服務器之間的直線距離，Be為用戶設備與云服務器之間的信道帶寬。

任務i從本地設備卸載至云服務器執行時，總時延為：

本文的目標是任務執行總時間和設備的總能耗最小時的卸載策略。因此，目標函數定義如式（15）：

3 算法設計

將粒子群優化算法（particle swarm optimization，PSO）應用到移動用戶任務卸載的現實場景中，傳統粒子群算法容易早熟，導致局部最優解[14]。為了解決這個問題，本文中引入遺傳算法中的交叉操作，將粒子根據適應度進行分級，適應度低的粒子經過交叉重組后得到適應度好的粒子進入適應度高的等級中，這樣得到的種群中的粒子適應度較優。因此，在粒子群算法快速收斂并保持較好的全局搜索能力的同時，結合遺傳算法選擇交叉的思想能夠提高算法的精度，并跳出局部最優。

3.1 傳統粒子群算法

粒子群算法是一種常見的傳統智能算法，在PSO算法中設置粒子種群數量，粒子的位置與速度。第i個粒子的位置Xi和速度Vi分別表示目標優化問題的解和粒子i位置的更新方向以及距離，Pbest表示粒子i自身最優位置，Pgbest表示整個種群搜索到的最佳位置。在每次迭代中，粒子i速度和位置更新公式如式（16）、（17）：

其中，c1、c2為學習因子；r1、r2為0～1 之間的隨機數；ω為慣性因子（ω較大則全局搜索能力強，ω值較小時局部搜索能力強）。

3.2 粒子編碼

本文采用浮點數編碼方式，每個粒子對應任務分配方案。文中用0、1、2、3表示4種不同的卸載方案，0表示任務在本地設備執行，1表示任務在邊緣服務器執行，2表示任務在異地邊緣服務器執行，3表示在云服務器執行。假設任務集合有7 個任務（n=7）T={T1,T2,T3,T4,T5,T6,T7}，對應的粒子編碼為χ=[1.1，2.0，3.2，4.0，5.1，6.1，7.3]，其中整數部分表示任務Ti{i∈[1,n] }；小數部分表示任務的執行位置（取整數）。例如編碼χ=[1.1，2.0，3.2，4.0，5.1，6.1，7.3]，根據上述編碼過程可知：T4和T2在本地執行（任務t4先于t2執行可根據關系矩陣判定）；T1、T6、T5在邊緣服務器執行；T3在異地邊緣服務器執行；T7在云服務器執行。

3.3 適應度函數

本文中所要解決的問題的是得到最優的卸載策略，由建立的模型可知，目標函數值f越大，系統總成本越大，卸載方案越差；反之亦然。因此，將目標函數的倒數作為適應度函數。其中，f的最小值不為0。

3.4 分組交叉重組

在常用的進化算法中[15]，選擇操作是把相對較好的區域與較差區域區別開來并將較差的區域直接淘汰。但是進行選擇操作將較差區域的粒子淘汰后，粒子種群的豐富性就會降低。為了提高粒子種群的優越性與多樣性，在本文所提出的改進算法中，先通過各個粒子的適應度值的高低將粒子分為兩個小組。第1 組為適應度高的粒子，第2組為適應度低的粒子，迭代時用第1組粒子的位置和速度矢量取代第2組粒子的對應矢量，并且不改變其個體極值。在執行遺傳思想的交叉重組操作時，第2 組粒子進行兩兩配對重組，子代粒子與父代粒子進行適應度對比，選取整組中適應度高的一半粒子進入第一組。通過交叉重組使得第1 組中的粒子種群適應度優于分組前，能夠增加粒子種群的優越性和多樣性，防止陷入局部最優并使收斂速度增加。粒子分組交叉過程如圖4所示。

其中，X和V分別為位置與速度矢量；child1(X) 和child2(X)為子代粒子的位置；child1(V)和child2(V)為子代粒子的速度；p是均勻分布的隨機數向量，為交叉概率，并且每個分量都在[0，1]取值；子代粒子的位置由父代粒子位置的算數加權和計算[16]。

進行交叉操作過程如圖5所示。

粒子交叉重組后得到的Pbest和Pgbest，根據粒子與速度更新公式進行全局學習，通過交叉重組操作后可以跳出局部最優，以更快的收斂速度找到優化問題的最優解。

3.5 算法流程設計

CRPSO算法參數與卸載策略參數的對應關系如表2所示。

表2 算法參數與卸載策略參數的對應關系Table 2 Uninstall policy parameter relationship

基于CRPSO算法的優化策略流程，具體如下。

輸入：請求任務數量n、移動設備的計算能力fl、邊緣服務器的計算能力fe、云服務器的計算能力fc、本地設備計算功率pl、邊緣服務器的計算功率pe、云服務器的計算功率pc。

輸出：最優卸載策略，最優適應度值。

步驟1 初始化。確定迭代次數和粒子的數量，并初始化粒子的速度和位置。

步驟2 計算每個粒子的適應度值，并比較各個粒子的適應度值，記錄其當前個體極值Pbesti和群體最優粒子Pgbest。

步驟3 執行分級交叉重組操作。

步驟4 根據公式（15）和（16）更新交叉重組之后新粒子的位置和速度。

步驟5 計算交叉后粒子的適應度，更新個體極值Pbesti和全局極值Pgbest。

步驟6 終止條件判斷。檢查是否滿足迭代次數，若滿足則執行步驟7，若不滿足，執行步驟3。

步驟7 輸出全局最優適應度和最優任務卸載策略。

4 仿真與結果分析

根據以上模型中假設的服務器的數量以及模型中涉及到的參數，在本節的仿真場景中，由于用戶在通信小區內的移動性較小，因此忽略移動過程中通信鏈路軟硬切換帶來的影響，只關注任務卸載的過程，并假設所有邊緣服務器的計算能力都是相同的，本地終端設備為3個，邊緣服務器數量為8個，1個云服務器。

在文獻[17]的基礎上設定系統的基本參數，并結合本文所建立的任務卸載模型，將實驗環境適當調整后，對本文所提出的CRPSO 算法以及Local-MEC 算法、ECPSO 算法、GCPSO 算法利用MATLAB R2020a 仿真平臺進行了仿真對比實驗。任務卸載的仿真參數由表3給出，CRPSO算法的相關參數由表4給出。

表3 算法相關參數Table 3 Algorithm related parameters

表4 實驗仿真參數Table 4 Experimental simulation parameters

Local-MEC算法：任務卸載至本地設備的計算卸載策略。

ECPSO（Edge Computing PSO）算法：邊緣計算中基于傳統粒子群算法的計算卸載算法。

GCPSO（Genetic Cross PSO）算法：邊緣計算中基于遺傳的改進粒子群的計算卸載算法。

4.1 任務數量改變對系統總代價的影響

為了研究任務數量的變化對系統總代價的影響，設置模擬的任務數量分別為25、50、75、125、150（個），利用CRPSO 算法、Local-MEC 算法、ECPSO 算法、GCPSO 算法進行性能比較。仿真結果如圖6所示，隨著任務數量的增加，系統的總代價逐漸增加，這是由于任務數的增加將會導致任務在卸載過程中消耗的能量和處理任務的時間會增加。從圖中能夠看出，與Local-MEC 算法、ECPSO 算法、GCPSO 算法相比，本文提出的CRPSO 算法的系統總代價是最小的，約為Local-MEC 算法的11.91%、ECPSO算法的36.79%、GCPSO算法的56.24%。

4.2 迭代次數對系統總代價的影響

本節中為了更好地顯示迭代次數對系統總代價的影響，取最大迭代次數G=100，總任務數n=80，時延與能耗的權重系數ω=0.5。由于Local-MEC 算法中任務只在本地設備和邊緣服務器執行卸載策略，迭代次數對實驗結果的影響省略。仿真結果如圖7所示，隨著迭代次數的增加，CRPSO算法、ECPSO算法、GCPSO算法的系統總代價都逐漸減小。從圖中可以看出，迭代70 次之后，系統總代價趨于平穩。因此，當迭代次數為70時，可以得到系統最優解。

4.3 工作量對系統總代價的影響

任務工作量的大小對系統總代價也是有影響的，在本節中取任務工作量在[0，100]之間，任務數n=100，ω=0.5，從圖8 可以看出，任務工作量的增加，設備的能耗會隨之增加，由于計算量較大，執行時間也會增加，故而系統的總體代價也逐漸變大。從圖中可以看出，CRPSO算法得到的系統總代價最小，約為Local-MEC算法的13.1%、ECPSO算法的31.8%、GCPSO算法的76.5%。

4.4 異地邊緣服務器對系統總代價的影響

本文提出的邊緣協同的框架下，離用戶最近的邊緣服務器周邊服務器的數量也會對系統總代價產生影響。考慮到若附近邊緣服務器的數量為0時，邊緣服務器之間的協同卸載則不能執行，因此本節中附近邊緣服務器的數量設置為1～7個進行仿真實驗，由于傳統卸載策略不受周邊服務器數量的影響，所以在圖中略去。仿真結果如圖9所示，當附近邊緣服務器的數量為3個時，系統總代價最低，可以輸出最優卸載策略；隨著附近邊緣服務器的數量不斷增加時，任務卸載時服務器之間的傳輸時延與能耗增加，導致系統總代價升高，當附近邊緣服務器的數量為6個時，系統總代價有略微的升高就是這個原因。但是從圖中可以得到，本文提出的CRPSO算法卸載策略系統總代價始終是最低的。

4.5 時延與能耗權重比對系統總代價的影響

在對系統總代價產生影響的因素中，時延與能耗權重比值也是需要考慮的重要因素之一。本節主要研究時延與能耗權重比ω/(1-ω)在[0.01，100]時，ECPSO 算法、GCPSO算法、CRPSO算法的性能比較。仿真結果如圖10所示，隨著時延與能耗權重比值的增大，CRPSO算法的系統總代價約為ECPSO 算法的33.1%，GCPSO 算法的58.9%，明顯優于上述算法。因此，CRPSO 算法能夠對不同場景下的移動服務起到優化作用。

5 結束語

本文針對移動任務卸載的時延與設備能耗的優化問題，及多個邊緣服務器與云服務的協同問題進行研究，提出了多個邊緣服務器的協同計算卸載方案，通過引進遺傳交叉思想對粒子群中部分粒子進行分組交叉取優，使算法跳出局部最優，更快收斂于全局最優解，得到最優卸載策略。仿真結果表明，CRPSO 算法的系統總體代價最小，可以在時延與能耗均衡的情況下輸出最優卸載策略。下一步工作將對卸載模型進一步完善，采用深度學習相關算法進行卸載策略研究。