分數的雙重含義在問題解決中造成的困擾及對策

李 梅

(江蘇省揚州市育才小學，江蘇揚州，225000)

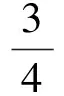
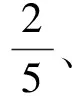
學生對分數的理解傾向分率的意義，而忽視數量意義，必然會對分數除法問題的解決產生不良影響，那么在教學中就要注重引導學生全面理解分數的雙重意義，使認識的“天平”達到平衡，從而幫助學生有效解決分數除法問題.

1 關注問題結構，讓學生學會有序思考

分數的雙重意義在應用題中對學生思考產生干擾的原因之一，就是學生在解決問題中沒有分清思考的主次.學生的注意力先被分數吸引了，于是把思考放在了對分數意義的揣摩上，而沒有首先分析題目中的數量關系，再把分數放入題目的整體關系中進行理解.因此，要注重引導學生在解決問題時采用“找關系——代數字”的解決策略和步驟，所謂“找關系——代數字”就是在分析題目時，通過認真審題，先從題目結構和數量關系入手，根據已知信息找出數量關系，然后把對應的數量代入數量關系式中，最后進行解答.這種先宏觀(對題目進行宏觀層面的結構分析，找出數量關系)再微觀(對題目微觀層面的運算)，符合學生認知規(guī)律，使學生的思考主次分明，減小了思考時的混亂.

2 建立多元表征，促進對分數的全面理解

學生對分數的理解偏向于分率意義，而忽視數量意義，這與學生學習分數的經歷有關.學生一開始接觸分數時，教材中就是借助分物的情景來定義分數的，把一個整體平均分成若干份，分數就表示其中的一份或幾份.而且在分數的后續(xù)學習中存在大量平均分的情景與問題，更加加重了學生對分數的分率意義的偏向理解.這種學習經歷使學生對分數的表征傾向于分物的動作性表征和形象表征，而沒有進一步建立起抽象表征，致使很多學生片面地理解分數.因此在教學中，老師要促進學生對分數表征進行多元建構，把學生從這種理解偏向中“拉回”到分數作為具體數量的意義上，讓學生全面地理解分數，使認識的“天平”達到平衡.

首先，利用數線模型，豐富分數的表征形式，讓學生在直觀表征的基礎上建立抽象表征.數線模型就是在線段上表示數，它是數軸的雛形.在學生的理解中，分數的模型一般是平均分之后的小棒、蛋糕等實物和面積等模型，這種直觀模型在學生初步學習分數時有利于學生對分數的分率意義的理解和掌握，但如果只停留在這一階段就會造成學生對分數膚淺理解.通過數線模型，把分數在線段上用一個個點表示出來，是一種抽象表征，需要更高的抽象能力，有助于打破學生直觀認識分數的思維定勢，實現分數、小數、整數之間的意義聯(lián)通.

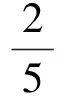
3 合理設計題組，在對比中加深理解

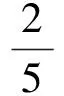
其次，給學生呈現這樣的題組，一組是題目里沒有分數的題目，題目是學生熟悉的，這種題目可以喚醒學生已有相關經驗，從而順應學生學習過程和思維過程.另一組是題目里有分數的題目，但兩道題目的問題結構是相同的.然后讓學生自主解決，進行對比，感受分數在問題解決中的意義.

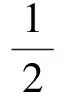
做完兩道題后，讓學生進行對比分析，兩道題目除了數字上有變化之外，其他沒有任何變化，這樣把整數、小數、分數放入同一道題目中，學生通過分析比較就能發(fā)現分數和整數、小數一樣都能表示具體數量的大小，就會減少分數雙重意義的干擾.