對八年級學生學習實數的現狀分析

王興樂，袁曉龍

(蘭州市第九十二中學，甘肅蘭州，730060)

數學概念是整個數學知識結構的基礎，作為學生進行數學思維的核心，它不僅是數學思維的產物，同時是更高層次的數學思維的工具.概念的獲得和有效理解掌握，可以幫助學生在沒有直接現實經驗的條件下獲得抽象觀念，同時已掌握的概念又成為學生學習新的概念時的起點，成為學生發現或同化新知的“固著點”.學生只有透徹地理解數學概念，才能形成正確的邏輯論理，形成空間想象能力，把握住后續的運算技能，本文從八年級學生實數的測試情況進行了以下分析.

1 實數相關概念的學習現狀分析

學習生活中由于數的不夠用而產生了實數，有理數與無理數是截然不同兩種數，無理數的出現進一步補充了原有的數系.所以在已有基礎之上，對其進行了規范，定義為有理數與無理數統稱為實數，所以實數概念的定義，看起來是矛盾的，實際上它們又是對立統一的.

通過測試，了解到學生對實數的相關概念認識模糊不清，區別不開.如：

例1下列說法中，正確的是

( )

A.無理數是無限小數 B.有理數只是有限小數

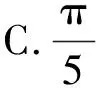
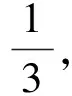
2 實數表示方法的學習現狀分析

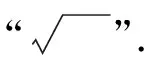
例25的平方根可以表示成.

( )

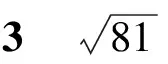
A.±9 B.9 C.±3 D.3

在這個問題的作答中，近四分之一的學生選項為A，沒有徹底的理解問題，將此理解成為了81的平方根去做了.對于題目中的運算意圖沒有掌握跟理解，在實際運算在只進行了一次運算.由此，我們可以清晰地知道，八年級的學生對于平方根的符號表示還不夠熟練.

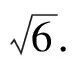
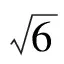
3 實數分類標準的學習現狀分析

實數的分類有兩種：分為有理數與無理數，按照定義來分類；另外一種就是根據與0的大小來分.如：

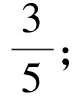
有理數有無理數有

整數有實數有

通過批改學生作業發現，學生對于實數的正負符合表現形式理解的比較清晰，歸納分類的準確度是比較高的.但對于無理數和有理數的分類，準確率還不到50%.通過深層次的分析，發現在這其中存在以下幾個具體的問題：

(2)處理0的劃分不夠好

八年級的大多數學生在整數的分類上，最容易遺漏就是0這個特殊的數，我們知道，0它不是正數也不是負數.0它是整數也是有理數，它具有多方面的意義.有的學生會將0劃分到無理數當中去，受定勢思維的影響，學生普遍認為在正無理數與負無理數之間應該會有個0的.

(3)關于無理數的表現方式

特殊符號π與3.14的區別；開方開不盡的數與根號下的數的區別；怎樣才算是無限不循環，在這幾處學生們都容易出現混淆.另外并不是所有的無理數都可以寫成帶根號的形式，還有就是無理數也包含具有特定意義的數，比方π，2π等，無理數也包含一些特定結構與規則的數比方說該題中的“0.202 000 200 000 2……(相鄰兩個2之間0的個數逐次增加2)”，學生們容易漏掉.可見，部分學生對于無理數的表現形式認識得不夠徹底.

(4)關于分數的歸類

(5)類似開方運算的歸類

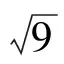
4 實數運算的學習現狀分析

初中生對于四則運算掌握的較好，在加入實數運算后就顯得不容樂觀了.通過觀察測試卷實數的運算，顯著的問題具體如下：

(1)運算順序不清楚

先要進行乘除，然后在進行加減，對于同一級的運算我們應該依次進行運算，我們說有分母就去分母，有括號的情況下，就先算括號里面的.部分學生對我們常說的運算要求不是很理解，一通亂算，有進行完加減再進行乘除的.

(2)不清楚去括號法則

復雜實數運算的技巧之一就是去括號，主要依據就是乘法對加法的分配律，在其運算過程中運算符號起著決定性的作用，分不清符號的話最容易產生運算錯誤，也是實數運算中的一個難點所在.歸結下來有以下幾種：

a.當括號前面有負號存在的時候，學生在去括號的時候不是說忘記變號，而是忘記里面的各項都要變號，尤其在根式化簡里面最為常見.

b.如果括號前面的系數不是1的話，我們在去括號時，沒有合理利用乘法的分配律將我們括號內部的所有的項都進行分配.

c.另外就是有括號跟沒括號對于有的學生來說沒有任何影響，直接去掉，各項都原封不動，這個時候反映的就是此類學生對于去括號有沒有依據根本不清楚.

(3)逆向思維不靈活

思維定勢的緣由導致部分學生將各種運算律都不能逆向使用，出現此類的運算就蒙圈了，不知道如何是好，胡亂寫出答案.

(4)不明確運算的性質

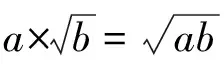
除此之外，學生還存在一些其他方面的問題.如錯誤的理解“帶分數”的意思，有理數的合并與無理數的合并相提并論；計算器使用不當的，計算器開方是課程改革后新加進來的，基本掌握的還是很熟練，但在復雜的問題上還是會出現錯誤的；在二次根式的運算當中，尤其是化簡不知道什么時候運算就終止了，分辨不出最終的結果；合并同類項與最簡二次根式的區別，根式化簡與平方根之間的區別也有不清楚的學生，以至于運算結果錯誤.

通過測試，本文主要分析了以上四種情況，后續還會對其他情況進行詳細分析，希望分析的這些情況能為新課改后的概念教學提供一些幫助.