多思維視角切入，巧方法破解題目
——一道最值題的探究

梁禮華

(福建省福州瑯岐中學，福建福州，350017)

雙變元代數式的最值(最大值或最小值)問題，一直是歷年高考試題中一道亮麗的熟悉“面孔”.破解此類最值問題，常見的破解思維是借助基本不等式、函數或方程、三角函數以及導數等工具與思維切入，合理融合相關的數學知識，從數學知識、思維方法與能力等方面加以交匯與綜合，恒等變形，巧妙處理，正確破解.

1 問題呈現

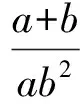
2 問題剖析

此題題目條件簡單明了，通過兩正實數所滿足的二次方程關系，利用雙變元之間的對應關系來確定其對應分式代數式的最值或最值范圍問題.這里，題目條件關系式與結論關系式之間沒有明顯的過渡或聯系.

解決此類問題的關鍵就是如何在已知條件的代數關系式背景下，通過認真審視試題條件，構建題目的條件與結論這兩者關系式之間的“橋梁”，對相關的代數關系式進行合理的恒等變形，利用參數之間的關系轉化與合理切入，巧妙處理.在不同的數學思維視角下，如基本不等式、函數或方程、三角函數以及導數等思維方式，進而確定不同的解題思維與對應的精彩解法.

3 問題解決

思維視角一：基本不等式思維

利用基本不等式來確定相關雙變元代數式的最值問題，是解決此類問題中最常用的技巧與方法.解決問題的關鍵就是合理配湊條件與結論之間的關系，以及基本不等式成立的條件.利用基本不等式思維來處理問題時，有時可以直接利用，有時需要通過換元法、消元法等來綜合與應用.

解析：

方法1：換元+基本不等式法

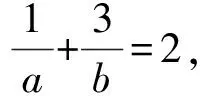
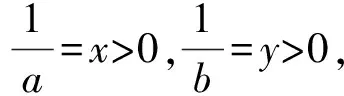
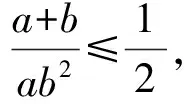
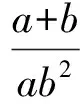
方法2：消元+基本不等式法

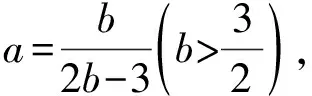
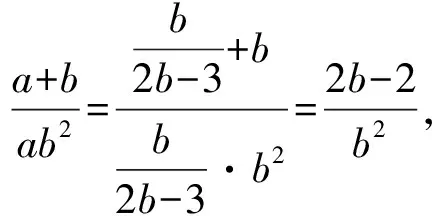
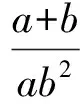
方法3：代“1”+基本不等式法

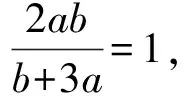
根據基本不等式，有(b+3a)2=(b+a+2a)2≥4(b+a)·2a，

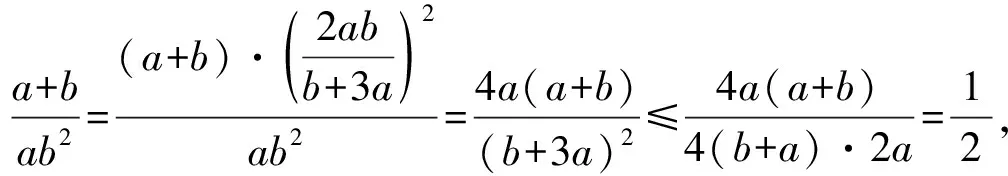
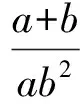
評析：涉及雙變元代數式的最值問題，最常見的思維方式就是借助基本不等式思維來處理.解決問題的關鍵在于通過對代數關系式的合理恒等變換，與結論對應的分式關系式加以聯系，借助相應的技巧方法，或換元處理，或消元化簡，或代“1”變換等，構建利用基本不等式的條件.

思維視角二：函數思維

利用一些特殊函數的圖象與性質來確定相關雙變元代數式的最值問題，是函數的圖象與性質的進一步掌握與綜合應用.解決問題的關鍵就是進行合理變形，轉化為涉及其中一個參數的函數問題，利用特殊函數(如一次函數、二次函數等)的圖象與性質來解決.特別的函數模型所對應的圖象與性質是解決此類問題的基本數學模型.

方法4：二次函數法

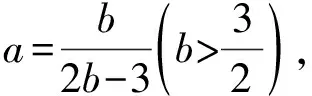
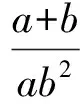
評析：涉及雙變元代數式的最值問題，函數思維是破解問題的一大基本技巧與策略.通過對代數關系式的合理恒等變換，或整體代入，或關系式轉化，進行巧妙的合理消元，轉化為涉及其中一個參數的一元二次函數問題，借助配方處理，利用二次函數的圖象與性質等來確定對應的最值問題.

思維視角三：方程思維

利用方程來確定相關雙變元代數式的最值問題，是初中方程與高中不等式求解的綜合應用.解決問題的關鍵就是利用所求的結論關系式引入參數，構建涉及其中一個參數的方程(一般是一元二次方程)，利用方程有根的判別式法來構建不等式，通過不等式的求解來分析與解決.引入參數，待定系數法，綜合不等式的求解是關鍵.

方法5：方程的判別式法

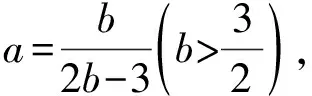
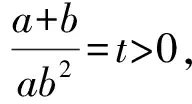
由于以上關于參數b的二次方程有正實數根，

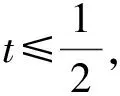
評析：涉及雙變元代數式的最值問題，方程思維也是破解問題的一大基本技巧與策略.通過對條件中的代數關系式的合理恒等變換，結合所求的代數關系式的設元處理引入參數，進而利用消元，轉化為涉及其中一個參數的二次方程問題，利用二次方程有根的判別式法等來確定對應的最值問題.

思維視角四：導數思維

利用導數來確定相關雙變元代數式的最值問題，是解決此類問題中最“萬能”的一種技巧與方法.解決問題的關鍵就是合理消元，將所求的代數關系式轉化為涉及其中一個參數的函數關系式，通過求導處理，結合函數的單調性來解決最值問題，往往運算量比較大，過程比較繁雜.

方法6：導數法

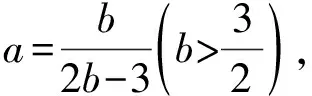
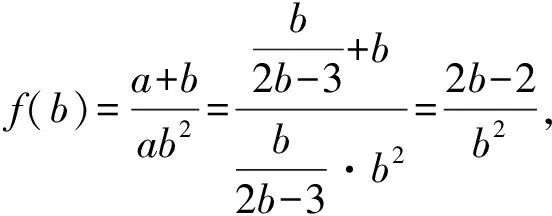
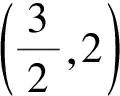
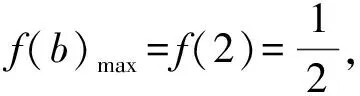
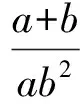
評析：涉及雙變元代數式的最值問題，結合關系式的轉化進行消元處理，將所求代數關系式轉化為一元關系式，構建函數關系式，通過函數求導運算與轉化，利用函數的單調性、極值以及最值等相關知識來確定對應代數式的最值或取值范圍.

4 變式探究

探究1：根據條件改變所求解的代數關系式的形式，從另一個層面來求解對應代數式的最值問題，與原題在知識點考查、試題難度、思想方法應用等各個方面都比較相似.

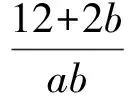
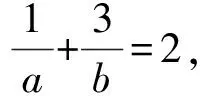
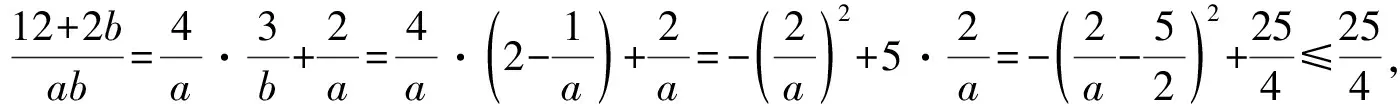
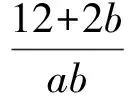
評析：根據條件中代數關系式的變形與轉化，對所求解的代數關系式的變形進行消元處理，通過配方，利用二次函數的圖象與性質來確定最值問題.當然，也可以參照原問題的解析的不同思維視角，嘗試利用其他相關的方法來分析與解決，也可以達到解決問題的目的.

探究2：保留問題的條件背景，改變原來求解的分式代數式中的分子與分母的位置，得到以下對應的變式拓展問題.該變式問題考查的知識點與原題基本相當，但由于格式更加難變形，試題難度有所提升.

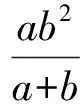
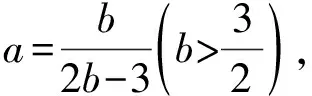
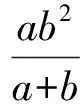
評析：利用所求分式關系式為正數的情況，與原來所求的代數式互為倒數，從而可以采用函數關系式的變形，結合二次函數的圖象與性質來分析與解決.在原問題的基礎上分析與解決，難度就比較大，可以嘗試從其他思維方法來解決.

探究3：保留問題的創新情境，引入對應的參數來構建條件中的代數關系式，使得問題更具一般性，得到以下對應的變式拓展問題.該變式問題考查的知識點與原題基本相當，而試題難度有所提升.

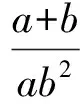
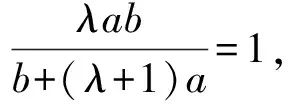
根據基本不等式，有[b+(λ+1)a]2=(b+a+λa)2≥4(b+a)·λa，

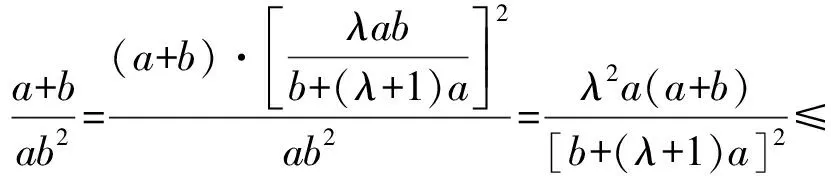
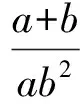
5 教學啟示

5.1 總結技巧策略，形成思維習慣

此類涉及給定方程關系式的雙變元或多變元的代數式最值或取值范圍問題，命題新穎，背景變化多端，破解思維奇思妙想，破解策略多樣，切入多變，方法精彩紛呈，殊途同歸.具體解答時往往是結合題目條件給出的代數式(整式、分式、根式等)的基本特征(定和、定積、定比例等)，合理恒等變形與巧妙轉化，正確數學運算與合理推理，借助一些相關的數學思想方法，綜合一些常見技巧策略加以應用.

5.2 提升解題能力，形成學科素養

在解決一些相關的數學問題中，我們要不斷積累、比較、總結、提升，總結技巧方法，歸納類型，總結并形成“多題一解”“多類一法”等，做到具體解題時有“法”可依，有“據”可查.巧妙融合與交匯相關的數學基礎知識、思想方法等，學會應用思想方法等“武裝”頭腦，不斷提升數學的解題技巧以及數學能力，舉一反三，融會貫通，靈活變通，真正形成數學體系，提升數學能力，培養數學學科素養.