初中數學“整體法”解題思路分析

陳 宇

(江蘇省南通市幸福中學，江蘇南通，226001)

整體法是初中數學中常用的一種解題方法，這種方法將問題看作一個完整的整體，注重問題的整體結構和結構改造，特點是可以宏觀上全面觀察事物的整體結構，從而揭示事物的本質[1].初中數學和高中以及小學數學有著很大的不同，小學數學更多地注重學生的逆向思維，高中數學更側重于學生正向思考并解決問題，而初中數學則需要完成這個過渡.初中數學有很多種解決的方法，而方法的選取決定了解題的上限，運用好的解題方式可以更加方便快捷.整體法就是解決初中部分數學問題的一種非常便利的方法.靈活運用整體法可以提高數學分析能力和解決能力.整體法在初中數學的應用主要可以從以下幾個方面進行展開.

1 整體法在代數式求值中的應用

代數式求值是初中數學中最為重要的知識點，在解決此類問題時，利用整體法可以有效進行化簡求值，其中整體代入可以更快捷地解決部分問題.整體代入的解題思路是將一個代數式作為一個整體，然后將這個整體的值代入到另一個代數式中進行運算，具體案例如下：

例1已知a2+5ab=16，并且3b2+2ab=50，求a2+11ab+9b2的值.

題目中出現兩個未知數a和b，在正常的解題中，需要通過兩個代數式結合計算出a和b相對應的代數值，再代入到最后所要計算的代數式中進行解析，計算起來相對繁瑣.

現采用整體法對這道題進行解題分析，首先將兩個代數式a2+5ab=16和3b2+2ab=50看作兩個整體A和B進行分析，然后可以發現最后所求的代數式a2+11ab+9b2，可以由一個整體A和三個整體B進行相加得到，即a2+11ab+9b2=(a2+5ab)+3×(3b2+2ab)，因此可以很方便地求出最后的函數值為166.

因此，在解題時，學生的思路應該時刻保持清晰，能夠準確地把握題中的要點，結合整體法的思路對代數問題進行分析，找到解決問題的捷徑，進而快速準確地完成解題.

2 整體法在因式分解中的應用

整體法在函數中的運用還可以體現在初中數學最重要的解題要點——因式分解中，因式分解在很大程度上運用了數學的整體思想，把重點放在問題的整體上，多方位思考，進行整體變形，多角度探究，最終確定解題的策略，進而解決問題.

例2分解因式(x+1)(x+2)(x+3)(x+6)+x2

題干中可以發現如果將每一個括號內的代數式分別進行相乘最后再進行分解因式會顯得非常困難，這里我們可以進行分組，當(x+1)和(x+6)相乘以及(x+2)和(x+3)相乘可以得到相似的內容，因此可以先將這兩部分進行組合計算，得到的展開式再利用整體進行運算即可，具體的解題過程如下：

解：原式=(x+1)(x+2)(x+3)(x+6)+x2

=(x+1)(x+6)(x+2)(x+3)+x2

=(x2+7x+6)(x2+5x+6)+x2.

設(x2+6x+6)為a，

那么原式=(a+x)(a-x)+x2

=a2-x2+x2

=a2

=(x2+6x+6)2.

通過上述問題的解決，可以發現因式分解的過程中應該特別注意整體法的應用，結合整體代入的方法，不僅可以簡化運算，而且能夠有效地避免由繁瑣的運算帶來的弊端.將部分算式看作整體，在實際解題中有著很大的作用.

3 整體法在解方程中的應用

初中數學離不開方程的運用，解方程的題目類型多種多樣.很多解方程的問題，也會運用到整體法，在解方程的過程中，韋達定理對于學生一定不會陌生，這種利用根的性質所運用的定理，同樣利用了整體法的性質，從而使問題更加容易解決.

例3若m是方程2x2-3x-1=0的一個根，則6m2-9m+2 022的值是多少？

題目中可知m是方程的一個根，因此將m代入到方程中，一定成立，而代入后通過比較已知方程和需要求解的方程，會發現二者存在數量關系，然后利用整體法直接代入可以得出所求方程的值.利用整體法可以免去計算未知數的值，整體代入求出所需值，提高了準確性.

解：2x2-3x-1=0

則2x2-3x=1，

將m代入可得2m2-3m=1，

原式=6m2-9m+2 022

=3×(2m2-3m)+2 022

=3+2 022

=2 025.

通過上述方程的解決，可以發現，合理地運用整體法的知識可以解決很多解方程的問題.計算過程中，對問題整體化考慮，可以將問題簡潔化，有時甚至可以不計算未知數的值就可以解出所需結果.在教學過程中要注意到學生使用整體法尋找最優解題的路徑，這可以拓寬學生的知識面，同時培養學生的發散思維.

4 整體法在分式方程組中的應用

處理部分分式方程組時，對方程組直接進行賦值計算會比較麻煩.這些較為復雜的方程組利用常規的計算既浪費時間，又容易出錯.如果可以利用整體法對問題進行簡化處理，然后再進行計算會使問題的解決變得更加容易.

例4甲、乙二人合作完成一項工程需要24天；若乙先干10天后甲再加入，則需要花費20天完成，問甲，乙單獨完成這項工程各需要多少天？

面對這類問題，首先想到的就是列方程組進行計算，接著進行解方程分別計算出甲、乙完成這項工程需要花費多少天即可.真正解題時會發現所得方程組為分式方程組，這時如果利用傳統解方程組的方法，并不容易求解，因此需要靈活變通，找到便捷的解題路徑，做到解題省時又省力.該題利用整體法就可以很好地解決，求解過程與分析如下：

解：首先需要假設甲、乙單獨完成這項工程各需要x天以及y天.

這時可以得到如下方程組

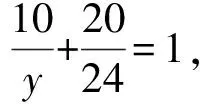
通過上述問題的解決，可以發現整體法在處理分式方程組的便捷之處.在實際教學工作中，教師應滲透整體的思想方法，提高學生的解題效率.

5 整體法在幾何問題中的應用

初中幾何問題是初中數學的難點，解決此類問題的困難之處在于做輔助線進行分析，但輔助線的選取對于學生來說是一個巨大的考驗，整體法同樣適用于解決此類問題.解決初中幾何問題經常會用到的方法就是整體補形法，這是整體法的一個分類.利用整體補形法對幾何問題進行分析，通過補形還原整體圖形的原有狀態，可以有效訓練學生的整體性思維，從而更好地對問題進行分析處理.

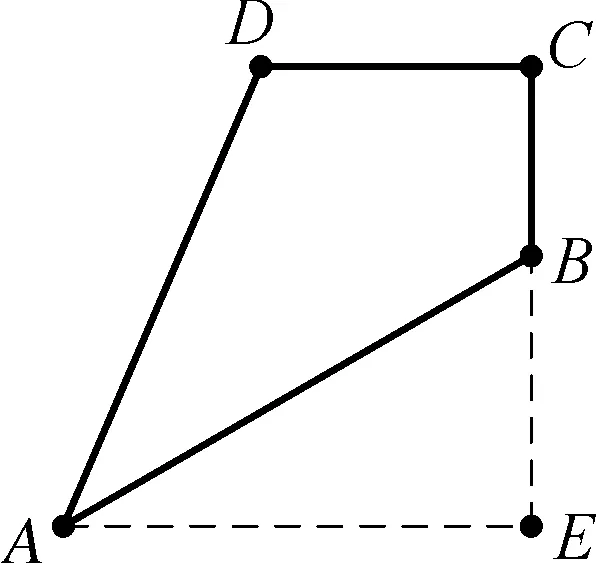
例5如圖，四邊形ABCD中，AB=2，BC=1，CD=1,∠ABC=120°，∠BCD=90°，求四邊形ABCD的面積.

從圖中我們可以發現，由于四邊形ABCD是一個不規則的四邊形，想要直接求出四邊形ABCD的面積是很難做到的.那么要想求出它的面積，首先就要進行組合或者拆分，將其轉化為熟悉的規則四邊形的面積.因此就需要利用整體補形法對其進行補形，然后再進行計算，具體解題思路和方法如下：

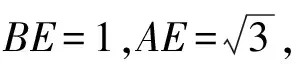
初中幾何問題中，利用輔助線解決問題是難點也是重點.大部分題目都是缺失輔助線導致很難分析，間接考慮這個問題就會發現，添加輔助線在大多數情況下都是在利用整體補形法將缺失部分補全，從而還原本身圖形進行分析.因此，學生掌握整體法的思維模式是解決幾何問題的重中之重.掌握好整體法的思路，會極大提高學生的空間想象能力，對于學生的解題技巧同樣會有所提高.同時，幾何問題對于學生們的智力開發也起到了非常大的積極作用，利用好整體法解決問題可以增加學生的學習興趣，除此之外，合理運用整體法進行解題也會使得不易解決的幾何問題更加清晰明了.

6 整體法在邏輯思維問題中的應用

整體法在一些思維邏輯問題上同樣可以起到意想不到的效果.在面臨很多相對復雜的問題時，將問題步驟細化會導致思考量增大，解決問題相對也不容易，但利用整體法思考，拋棄中間的步驟，將問題簡化，反而會有更好的成效.

例6王師傅開店，一雙鞋進價為30元，甩賣20元，顧客買鞋給了50元，王師傅找鄰居換了50元，事后鄰居發現這是假幣，王師傅又賠給鄰居50元，問王師傅虧了多少錢.

這個問題看似很簡單，但很多人都會走入誤區.很多學生習慣于把這個問題分開考慮，將問題細化到每一個交易環節，反而會使頭緒出現問題，最后出現錯算，少算以及誤算的情況.將問題進行整體分析，會發現在全部的交易中，導致王師傅虧損的只有甩賣以及收假幣兩個環節，其他部分找零錢以及換錢等環節都是平等交易，不涉及虧損，因此通過整體法分析，發現只存在假幣50元以及甩賣所賠10元，共計虧損60元.

通過上述問題，可以發現，很多思維邏輯問題都是給學生創造誤區，讓學生追求分析每一個步驟，反而忽略了問題的本身，做了大量無用功.而合理運用整體法，一方面可以幫助學生將復雜的邏輯梳理清楚，另一方面可以幫助學生對問題有更深層次的理解.能否將復雜的問題簡單化處理是一個學生的邏輯思維水平的重要體現.

7 整體法對于初中數學教學思考

在初中數學的教學中，整體法可以讓學生在解答各種類型問題的過程中，對所了解的知識內容進行整體分析和研究，可以有效提高解題的正確率和效率[2].初中數學的教學過程是一個漫長的過程，它需要老師和學生的緊密配合.解決問題的方法有很多種，整體法只是研究問題的其中一個方法，但整體法的應用，不拘泥于常規的解題思路，它可以更深層次地幫助學生建立做題的思維模式.

在對于初中數學習題的分析過程中，整體法一直都扮演著一個特殊的角色，它不僅僅是一種解題的策略，更是一種對于學生能力培養的有效方法.熟練運用整體法最大的優勢依然在于計算時間上的節省以及解題準確率上的大幅提高.

對于學生亦或是教師而言，數學是一個美麗的學科，是一個有魅力的學科，它最讓人流連忘返的地方在于它的多樣性，每道題的解題方法都不單單是某一種，整體法在龐大的初中數學解題方法中，也不過是冰山一角.很多學生會把這種方法當作投機取巧而不屑一顧，因為它似乎與傳統數學枯燥復雜燒腦的解題手段格格不入，但是整體法的靈活運用，摒棄了那些冗長繁瑣的步驟，它如同生活中“大道至簡”的理論一樣，將問題化繁從簡，更應該是初中數學教學發展的方向.

總而言之，整體法在初中數學的學習中是一種非常重要的學習方法.在解題方面，它可以提高學生解題的效率和能力，讓學生可以在題干中找到問題的關鍵點，把握住總體視角，也讓學生的解題思路更加清晰明確，省時省力的同時也提高了解決復雜問題的準確性.在教學方面，整體法的教學應該更高水準地應用于初中數學教學中，讓它不僅僅作為解題的一種手段.教師要能通過這種方法，提高學生的分析思考能力，構造學生的空間想象力，引導學生舉一反三，靈活運用所學到的知識，積累更多的經驗，實現一題一解.一題多解至一題優解的轉化.