一種基于SARIMA-LSTM模型的電網主機負載預測方法*

王 堃，鄭 晨，張立中，陳志剛

(1．中南大學計算機學院，湖南 長沙 410083；2．國網寧夏電力有限信息通信公司，寧夏 銀川 753000)

1 引言

隨著人民生活水平的日益提高，電力企業的業務規模在不斷增長，目前的系統運維水平已難以支撐多變的業務場景和問題。為了提高運維效率，許多研究人員開始致力于電力企業智能化運維研究[1]。時間序列的預測分析是其中重要的一環。目前，時間序列預測已經在工業環境中有了諸多經典的應用案例，如運用自回歸AR(Auto Regressive)模型[2]、滑動平均MA(Moving Average)模型[3]或自回歸滑動平均ARMA(Auto Regressive Moving Average)[4]模型進行負載預測。它融合了趨勢性、季節性等時間序列結構的先驗知識，對單一線性時間序列具有良好的預測性能。但是在現實場景中，內存等性能指標有著毛刺多、陡升陡降的特點。在預測這類復雜的時間序列數據方面,傳統方法無法利用時間相關的特征，難以捕捉數據間的復雜模式。

近年來，在主機負載預測方面，國內外的研究人員已經開展了廣泛的研究,并提出了一些行之有效的預測方案。文獻[5]將ARIMA(Auto Regressive Integrated Moving Average)模型與分類回歸樹CART(Classification And Regression Tree)[6]相結合，采用了加權最小二乘法[7]和邊界判定[8]進行優化，模型組合的方式彌補了自回歸模型無法擬合非線性信息的缺陷，大大提高了預測精度。這些方法反映出自回歸預測模型不斷完善、融合和創新的過程。

然而，這些方法的一個關鍵問題是誤差積累。在常見的統計學和機器學習方法中，大多數模型采用了滾動預測的策略。在預測過程中，將上一步的預測結果作為下一步預測模型的輸入，這種誤差的累積效應造成了數據的預測性能隨著預測距離的增加而急劇下降。因此，在優化時間序列預測模型結構中，如何在減少誤差積累的同時提高預測性能已成為當前研究的重要課題之一。文獻[9]在多步預測的基礎上，通過徑向基函數RBF(Radial Basis Functoin)神經網絡利用歷史預測誤差對未來時刻預測值進行修正，既解決了誤差累積問題，也提高了預測準確性。文獻[10]中的殘差遞歸神經網絡R2N2(Residual RNN)將傳統的AR模型視為初始預測變量，并使用遞歸神經網絡RNN(Recurrent Neural Network)估計殘差，從其實驗結論可以看出，對殘差的補償大大提高了時間序列預測的準確性。這2個方法為本文提供了研究思路。

在上述工作的基礎上，本文提出了基于誤差補償的周期性ARIMA——SARIMA-LSTM(Seasonal Auto Regressive Integrated Moving Average-Long Short-Term Memory)預測模型。首先,建立周期性ARIMA模型SARIMA將時間序列進行周期性分解，然后分開預測。周期預測采用解離出的周期波動值，趨勢預測使用ARIMA模型。對于SARIMA模型的預測誤差，本文采取了誤差自回歸預測的方法分析歷史誤差與未來誤差的關聯性。最終周期分量、ARIMA趨勢預測分量及誤差補償預測分量集成后得到預測結果。

2 方法與模型

對于給定的時間序列X={x1,x2,…,xn}，xi(1≤j≤n)表示n時刻時間序列的觀測值。本文建立的誤差補償負載預測模型主要是以時間序列X為輸入預測出n～n+v時刻數據值，并在一定程度上克服誤差累積效應,其中v表示預測時間步長。具體技術原理將在2.1節和2.2節詳細闡述。

2.1 SARIMA模型

ARIMA模型[11]是一種基于時間序列的預測方法,它由ARMA模型發展而來，用于解決實際生產環境中非平穩數據的預測問題[12],例如經濟領域內的GDP和進出口額等數據[13]。ARIMA模型的主要思想是通過差分方法消去序列的局部水平或者趨勢，再將差分后的序列應用到ARMA模型中，借此來實現非平穩時間序列的預測。ARIMA的建模公式如式(1)所示：

(1)

其中,yt代表時間序列X差分后在當前時刻t的值；μ表示常數值;p和q分別表示AR模型和MA模型的階數;et表示誤差值;γi表示自相關系數;θi表示相關系數[14]。

在此基礎上的SARIMA模型考慮了周期性因素的影響，是指一種預測周期性時間序列的模型。為了消除時間序列中的周期變動因素，一般采用STL(Seasonal and Trend decomposition using Loess)分解等方法進行趨勢解離、預測[15]。其變化周期用s表示。周期為s的乘積SARIMA模型建模公式如式(2)和式(3)所示:

(2)

(3)

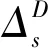
SARIMA的建模流程包括：數據預處理、周期性檢驗、平穩性檢驗、差分、BIC(Bayesian Information Criterion)準則[16]定階、建模求參和殘差檢驗。其中，周期性檢驗是SARIMA建模的重中之重，通過時序圖觀測法獲得周期值s，如圖1所示，橫坐標為1天的24小時，多條線段代表不同日期內每天的負載值變化趨勢。觀察發現,9點到18點存在2個明顯的波峰曲線，即存在明顯周期變化趨勢，周期值為12小時。本文采取ADF(Augmeted Dickey-Fuller)檢驗[17]，實驗數據經過一階差分就滿足了平穩性要求。

Figure 1 Daily periodogram of memory load time series圖1 內存負載時間序列的日周期圖

2.2 LSTM模型

LSTM網絡[18]，又叫長短期記憶網絡，是遞歸神經網絡RNN的一種變體，主要是為了解決在訓練RNN網絡時存在的梯度爆炸和梯度消失問題。這些問題會造成特征輸入RNN時,較早時間步的信息無法傳遞到較遠的時間步中，使得整個網絡可能遺漏掉極為重要的信息。

LSTM的核心在于它建立了一條貫穿所有時間步的信息流，通過門控機制控制每個時間步信息在信息流中的保留與刪除。整體的模型結構如圖2所示。LSTM在循環單元中采用了復雜的計算公式，其中最重要的核心結構被稱為細胞狀態(Cell State)。細胞狀態是貫穿LSTM單元的信息流，在圖2中用Ct-1到Ct的直線箭頭流表示。

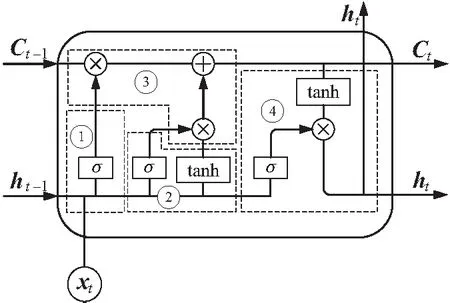
Figure 2 Structure of LSTM model圖2 LSTM模型結構

下面詳細介紹LSTM單元的具體結構：

(1)遺忘門(Forget Gate)。

在LSTM單元中，首先決定細胞要遺忘哪些信息。將上一單元的隱藏狀態ht-1和當前單元的輸入序列xt輸入遺忘門，經過sigmoid函數后生成輸出向量ft,其分量取值在[0,1]。向量中分量的值為0時，表示Ct-1的信息完全不保留；為1時，表示Ct-1的信息完全保留,具體如式(4)所示：

ft=σ(Wf·[ht-1,xt]+bf)

(4)

其中,σ(·)為神經網絡中的sigmoid激活函數，Wf表示權重參數。

(2)輸入門(Input Gate)。

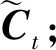
(5)

it=σ(Wi·[ht-1,xt]+bi)

(6)

其中,tanh表示神經網絡中的激活函數，WC和Wi表示權重參數，bC和bi表示偏置參數。

(3)更新門(Update Gate)。

經過遺忘門和輸入門后，確定了丟棄和更新的信息。接著對細胞狀態進行更新操作，得到Ct,具體如式(7)所示：

(7)

(4)輸出門(Output Gate)。

更新細胞狀態后，首先通過sigmoid函數處理輸入的ht-1和xt，得到判斷條件向量ot。然后，使細胞狀態Ct經過tanh函數，得到每個分量取值為[-1,1]的向量值，該向量與ot相乘，得到LSTM單元的輸出ht，具體如式(8)和式(9)所示：

ot=σ(Wo[ht-1,xt]+bo)

(8)

ht=ot*tanh(Ct)

(9)

其中，Wo表示權重系數，bo表示偏置系數。

綜上所述，LSTM通過其內部門控機制和模型循環結構，實現了具有長短期記憶的時間序列數據處理模型。

2.3 SARIMA-LSTM模型

ARIMA模型被廣泛應用于設備狀態預測中，通過差分方法處理非平穩數據，挖掘出歷史數據與預測數據的函數關系，實現數據預測并推測出置信區間。但是，傳統的ARIMA在進行多步預測時，存在誤差累積現象，難以滿足預測精度的要求。為此，本文提出了SARIMA-LSTM模型，首先，通過STL分解建立SARIMA模型;然后,對其進行誤差補償分析，利用誤差數據訓練LSTM神經網絡；訓練完成后，利用現有歷史誤差數據預測未來誤差；最后，結合SARIMA模型的預測值和LSTM的誤差補償值得到指標值未來12小時的預測值。

SARIMA-LSTM模型的建模流程如圖3所示。首先，進行數據預處理，刪除無關指標項后，取內存值每小時的均值作為該小時的指標值；然后，依據數據缺失狀況，采用K最近鄰插值法對數據進行補全；最后，輸出SARIMA-LSTM模型預測結果。

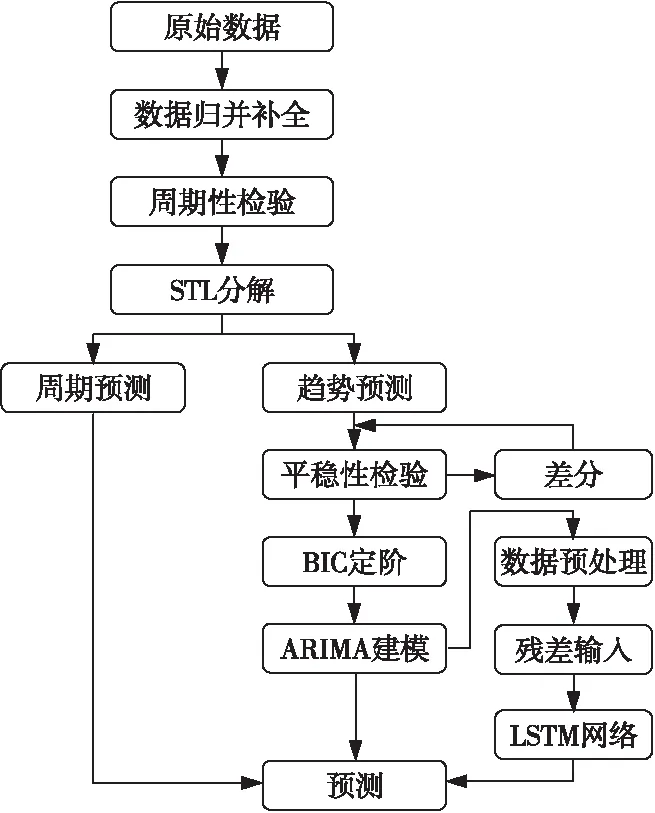
Figure 3 Flow chart of SARIMA-LSTM modeling圖3 SARIMA-LSTM建模流程圖

2.4 模型評價指標

本文的評價指標采用相對均方誤差RMSE(Root Mean Square Error)[19]和決定系數R2[20]。均方根誤差RMSE對一組預測結果中的極大或極小誤差比較敏感，它可以反映出預測的精密度和整體偏差大小。RMSE值越小，代表模型預測越準確。決定系數是用來衡量預測結果與真實樣本之間的相似程度，正常值處于[0,1]，結果越接近于1說明預測模型的擬合效果越好。2個指標的計算公式分別如式(10)和式(11)所示：

(10)

(11)

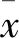
3 實驗與分析

本文將提出的SARIMA-LSTM模型應用于寧夏電力公司財務應用服務器的內存負載數據，采樣間隔為5 min。本文的所有方法基于Python3.8實現，實驗環境采用Windows10，AMD Ryzen 5 3550H with Radeon Vega Mobile Gfx 2.10 GHz，16 GB內存。神經網絡使用PyTorch 1.4.0+cu92實現。

3.1 實驗數據與參數

建模過程的數據信息如表1所示。

首先對實驗數據進行周期性檢驗，根據周期情況進行STL分解，得到周期分量和趨勢分量(包含隨機部分)。周期分量作為周期預測部分加入模型預測值中。在趨勢分量上，建立ARIMA模型預測趨勢部分，通過StateModels方法得到歷史數據預測誤差。在其基礎上，建立LSTM訓練集及測試集。輸入LSTM模型進行訓練。最后將周期預測值、趨勢預測值和誤差預測值累加在一起，得到多步預測結果。最終的預測公式如式(12)所示：

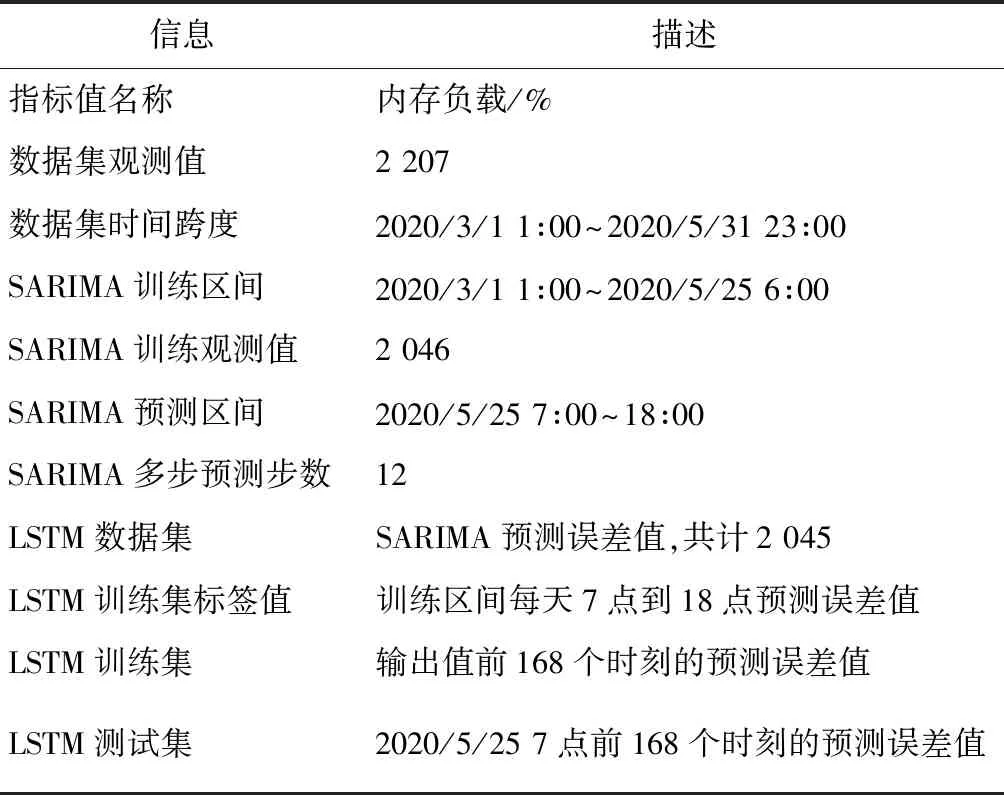
Table 1 Information of modeling data表1 建模數據信息

(12)

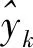
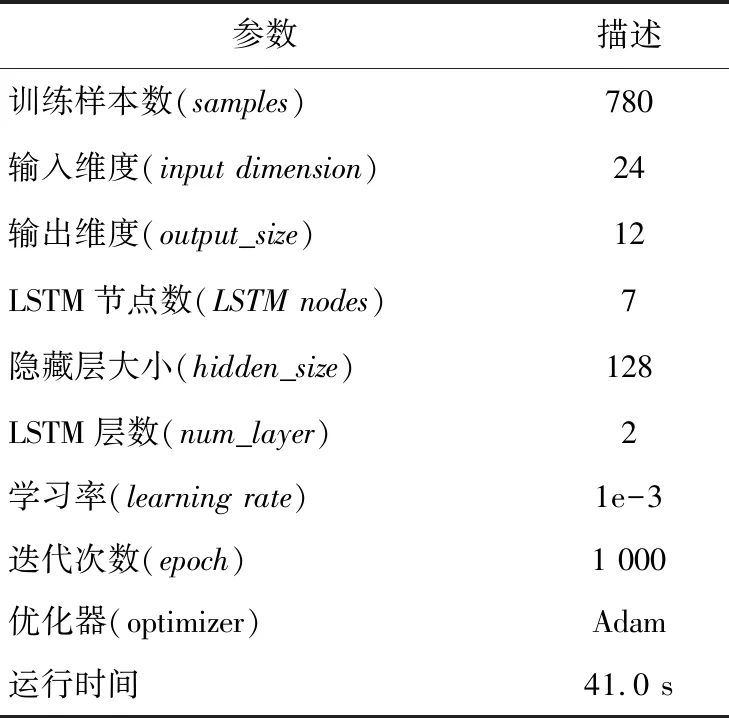
Table 2 Parameters of LSTM model表2 LSTM模型參數

3.2 數據預處理

圖4所示是2020年3月1日內存負載的波動變化圖。圖4a采樣間隔為5 min，數據上下波動劇烈;圖4b時間間隔為1 h，數值取每小時均值，數據波動平穩。對比可以發現,數據經過歸并后，消除了影響預測的數據抖動，又保留了大體趨勢。

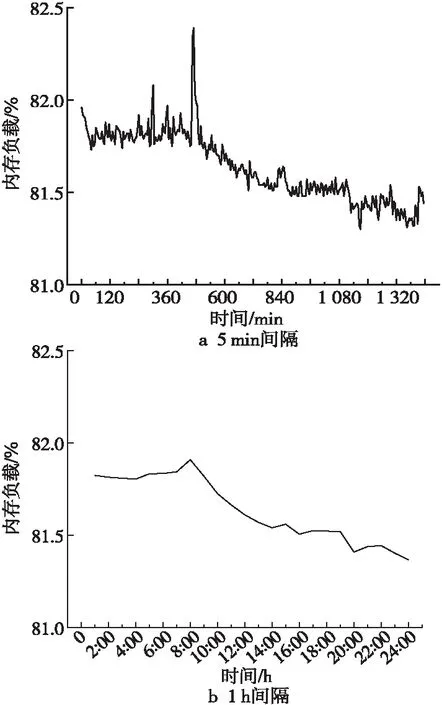
Figure 4 Memory load time series of 5-minute and 1-hour intervals圖4 5 min間隔和1 h間隔內存負載時間序列

3.3 實驗及結果分析

使用SARIMA-LSTM模型對預處理后的內存負載時間序列進行訓練和預測，預測誤差絕對值變化如圖5所示。

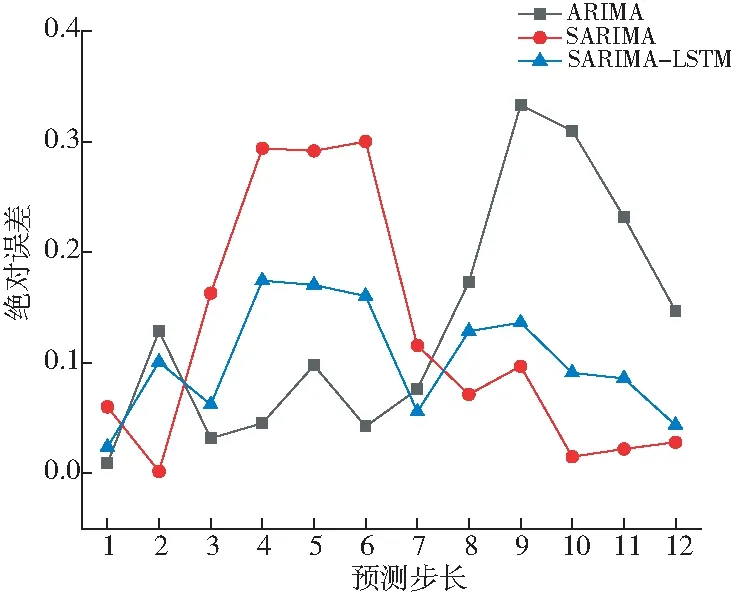
Figure 5 Variation of absolute prediction error圖5 絕對預測誤差變化

從圖5可以發現，ARIMA在進行前1～6步預測時，誤差較小，在6～12步時誤差值急劇上升，絕對誤差最大值為0.332 97，其預測效果需進一步提高。對ARIMA進行周期補償后，SARIMA模型前半段誤差增大，后半段的誤差顯著減小，整體多步預測效果相對于ARIMA提升不大。因此得出結論:SARIMA可以有效減少誤差累積，但周期變化會影響短期預測精度。而從圖像上看，SARIMA-LSTM模型前12步的絕對誤差值都小于0.2，整體預測性能高于其他模型。由此可見，SARIMA-LSTM能夠較好地權衡長期和短期預測效果，使得一段時間內的整體預測結果有顯著提升。

如表3所示，本文采用不同評價指標綜合比較不同模型的預測性能。在RMSE值上，ARIMA模型、SARIMA模型和SARIMA-LSTM模型的RMSE值分別為0.170 7,0.162 0和0.117 6，ARIMA的多步預測誤差最大，相比之下SARIMA-LSTM誤差下降了0.0531，這說明SARIMA-LSTM模型的誤差補償方法顯著提升了模型的預測效果。在R2值上，SARIMA-LSTM模型的R2值為0.564 6，在3種預測模型中數值最接近1，這反映出SARIMA-LSTM模型的擬合效果最好，優于其他模型。

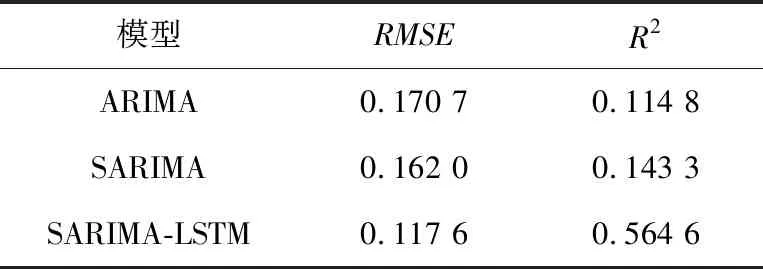
Table 3 Comparison of indicators of different models

除了模型預測性能的比較以外，本文還利用SARIMA-LSTM模型的預測結果生成了內存負載的動態閾值區間。如圖6所示，本文利用置信理論生成陰影區間，表示未來這一預測時間段的指標值有95%的可能性處于該區域內。首先，從真實值和預測值之間的對比效果來看，本文模型可以準確地預測內存負載在白天業務高峰期7點～18點的波動變化。其次，將95%置信區間作為閾值區間后，可以發現正常的指標值波動處于閾值區間內時不會觸發報警。而實際內存負載超出了該區間，說明發生了概率為5%的內存異常事件，系統通知運維人員進行設備運行狀態檢查。這種利用服務器內存歷史數據預測并估算設備運行指標動態閾值的方法，可以提高設備故障的預知能力，充分提升運維監控和故障搶修工作的主動性，提高了運維效率。

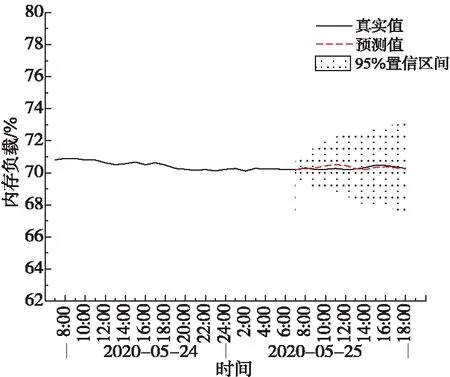
Figure 6 Prediction results of SARIMA-LSTM圖6 SARIMA-LSTM預測結果

4 結束語

本文借鑒了時間序列預測方向應用廣泛的預測模型以及誤差補償的前沿算法技術，提出了一種基于LSTM誤差補償的電網主機負載預測模型——SARIMA-LSTM模型。在綜合分析了電網主機負載數據的波動性和周期性后，建立SARIMA模型對時間序列趨勢、周期進行分開預測，再利用 LSTM誤差補償模型對SARIMA預測誤差進行自回歸分析。實驗數據中，以內存負載數據為例，驗證了本文所提出的模型在電網運維場景中的準確性和有效性。本文的未來研究工作如下：

(1)預測指標項。值得注意的是，本文的預測指標項為主機內存負載數據。業界常用的設備運行狀態指標還有CPU負載數據。下一步可以考慮進行多元時間序列預測，提高預測模型的穩定性和準確性。

(2)實時性。智能電網建立在集成、高速的雙向網絡上，需要運維人員能夠及時地發現問題甚至是預測問題。所以，需要在保證預測精度的情況下，降低預測模型的計算消耗，提高運算速度。

(3)自動化。電力運維系統逐步向高集成化、高智能化發展，先進的自動化系統可以實時調取歷史資料信息，建立信息分析平臺，防范未知風險。未來，先進的設備監控技術、信息決策技術、智能調度技術將在智能電網領域發揮巨大作用。