立足代數思維，學習《簡易方程》

徐斌

算術思維與代數思維有很大的差異，代數思維具有形式化、關系化、結構化的特點。布魯納說：“如果一門學科有明確的特征概念可以代表它，那么對這些概念的全面理解也就相當于對整個學科知識的理解。如果一門學科的知識根據某種固定的模式進行組織，那么充分理解這些模式會使適合學科設計的主要特定要素更清晰。”同樣地，掌握代數的思維方式，對小學生學習方程及今后系統學習代數知識，發展代數思維，具有戰略性的作用。因此，在《簡易方程》的學習過程中，要讓學生充分感受并學會用關系化思想分析問題，促進其思維從具體運算向形式運算過渡和適應。

一、認識方程：重構方程意義，直抵關系本質

什么是方程？教材給出的形式化定義：含有未知數的等式叫方程。很明顯，這樣的表述并沒有體現方程的價值與本質。因此，在課堂教學中需要引導學生通過反思，去體會方程的本質，重構對方程的理解，對概念的理解從“教學的數學”走向“學科的數學”。

在教授方程的概念時，教師就可引導學生感知方程的價值。如通過對列方程解決問題過程的反思，教師引導學生對方程重新認識與定義。除了及時組織學生對用算術方法解決問題與用方程解決問題進行比較，讓學生感悟到“未知數是否參與運算” “是否順著題目的意思列式子”等，還要讓學生結合解決問題的經歷，引導學生反思：列方程的依據是什么？方程能直接求出未知數嗎？你能用自己的話說說什么是方程嗎。這樣，對方程的理解與解決具體問題聯系起來。學生在反思中感悟到方程只是在表達關系，將題目中的數量關系用含有未知數的等式表達出來就行了，而不需要計算出結果。弗賴登塔爾認為，兒童的思維發展是跳躍性的，沒有內省，學生思維就不能實現跳躍而達到一個新的高度。對方程意義的重構，在于重新建立屬于學生自己的對方程的認識，以本質去代替形式，對方程的認識達到一個新的高度，思維方式也在發生著改變。

二、解方程：強化運作特質，走向形式運算

（一）抽象模型，反思運作意義

解方程的過程是形式化運作，分別把等號的兩邊看成對象，這與算術思維不同。很多學生由于受算術思維的影響，不習慣這樣的運作。“真正的數學頭腦是思維的頭腦，是內省的頭腦，這也是學校應當教學生的東西。”只有學生意識到每一次運作的目標與意義，他才能理解這樣的操作，而不是一種機械行為。反思就是把較低水平的活動看成較高水平活動的分析對象。在教學時，一要引導學生反思對比，解方程的過程與之前的計算過程中等號作用的不同之處，豐富學生對等號作用的認識。二是在進行方程的復習時，在對具體方程模式化表達的基礎上，對解法抽象分析從而達到一般化程度，有利于學生的認識與思維更上一個層次。

在復習課上，筆者讓學生小組內說一說：對解方程，你有哪些經驗值得與同伴分享？筆者讓學生舉例說出會解哪幾種類型的方程？再引導學生通過分類，將所學的方程分為簡單的方程與稍復雜的方程兩大類。接著引導學生抽象出這些方程的模型。

師：如果用字母表示這些數字，用x表示未知數，你能把這些方程表示出來嗎？

學生分別用字母概括出各類方程。

師：像這樣的方程，x±a=b，是如何解的？

生：兩邊同時加a或減a。

師：為什么要同加時或同時減a？

生：抵消，然后x就解出來了。

師：其他的簡單方程你會解嗎？

生：形如ax±b=c的方程，是在兩邊同時加或減b，把b消去，轉化為基本方程。

生：形如ax±bx=c的方程，是利用分配律進行合并，轉化為基本方程的。

師：是的，復雜的方程轉化為基本的方程，但是在具體轉化方法上面有所區別。

模型的深刻概括性本身對學習就具有數學意義，有利于學生思維水平的提升。而利用模型，進行方法的抽象總結，通過關鍵性問題：為什么要同時加或減或乘或除a？學生感悟到運作的意義是為了抵消，這樣直接說出了解方程的本質。通過比較，發現復雜方程都可以轉化成基本方程解決的，強調了轉化的方法，突出了運作思維。

（二）順勢而為，體會思維差異

蘇教版教材中有意回避了未知數在減數位置和除數位置的方程，因為利用等式的性質解決這兩類方程，涉及負數的運算，而小學又不涉及負數的運算，在教學中并不需要刻意回避。當學生在解決問題的過程中用到這樣的方程時，因勢利導，通過比較，讓學生發現異同，從而自己發現錯誤。在探討正確的解法時，有的學生提出，可以根據“減數等于被減數減差”直接求出未知數，實際上這是一種“倒過來想”的思路，其本質是算術思維。還有學生想出可以通過兩邊同加x，轉化成加法方程來求解。在對兩種方法進行比較的過程中，發現第二種方法其實是巧妙利用了等式的性質，轉化為加法方程，這樣讓學生進一步體會解方程運算的思維特點，把左右兩邊各看作一個對象，方程表示兩個對象的等價，解方程是通過運作進行轉化求出未知數，從而體會解方程運作的特點。

三、解決問題：價值引領，基本模型提升能力

（一）數形結合，感受基本模型的魅力

方程的背后是數量關系。只有讓學生掌握了從具體情境中抽取概括數量關系，才能列出方程。因此，抽取數量關系的能力，直接影響學生列方程的能力，也是學生思維水平的體現。如何找題中的數量關系？有的教師讓學生根據題目中的關鍵句尋找數量關系，如根據一些提示性語句（ ）比（ ）多（少）多少，（ ）和（ ）共多少，（ ）是（ ）的多少倍等。且不說一旦題目沒有這樣的“套路”表達，學生會一籌莫展，就算有這樣的語句，學生直接根據這些語句把握數量關系是有困難的，因為這些文字表達，與算術問題的表達沒有異樣，學生在面對這些文字時，受長期以來算術思維的影響，不自覺地就啟用算術思維方式，想到的是“是多少”的問題，即問題如何求解，如何求得答案等，而不是數量關系。因此，需要改變的是學生的思維方式，即建立結構化的思維，這樣才能讓學生的思維聚焦關系而非結果。

數量關系是實際問題的數學化表達，其實質是加、減、乘、除四則運算意義的運用。而學生在解決實際問題過程中，難以發現數量關系的原因就是因為無法透過情境，用思維把相關數學信息進行關聯并根據運算意義表達出來。教學中可以把這種基本的模型結構以一種恰當的方式，整體呈現在學生面前，當知識以整體進入學生的知識結構中時，其解決問題調用的也是整體而非部分。所謂整體，就是最簡的也是最本質的知識。在這里就是基本的數量關系模型，讓學生的認識通過基本模型，透過表面，直抵本質。如何才能發現眾多數量關系中的內在一致性而又利于學生接受呢？一是要去情境化，二是要具體化。兩者結合的最佳路徑便是直觀表達。直觀圖去掉了情境，直達本質，同時又直觀，又具體，符合兒童的思維特點。方程就是數量關系的符號化表達，而數量關系是半具體半抽象的，直觀模型則具有抽象與直觀的并存。

如通過不同類型的題目，引導學生畫出線段圖。

題目1：學校里買了18個籃球和20個足球，共付了492元，每個籃球14元，每個足球多少元？

題目2：一幢19層的樓房高57.8米。它的一樓是臨街店鋪，高為3.8米。其余18層平均每層高多少米？

題目3：兩輛車同時從同一地點向相反的方向開出，一輛車每小時行駛45千米，另一輛車每小時行駛50千米，幾小時后兩車相距237.5千米？

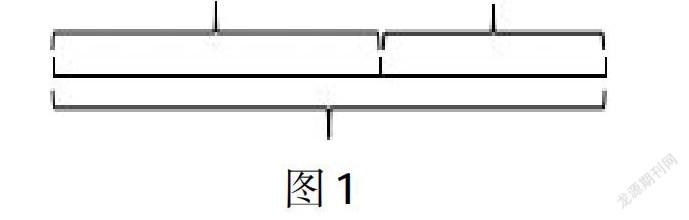
在隱去具體細節與情境后，如圖1所示。

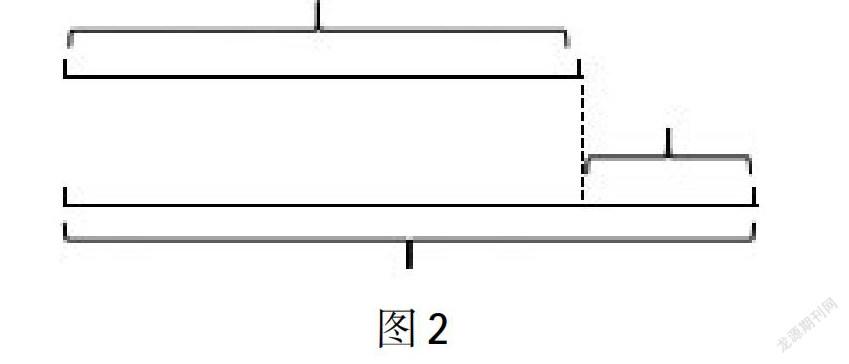
在此基礎上，引導學生進行反思：為什么這些題目各不相同，畫出來的圖卻是一樣的？學生在討論中感悟：其實這些題目都只不過在說一件事，即部分與整體之間的關系。這種直觀表達學生很容易發現三個量之間的三個不同的數量關系。在此基礎上，讓學生再回到現實，這樣的圖還可以表示哪些數學故事？從抽象到具體，用具體情境豐富對模型的認識，模型在學生思維中豐富，成為一種解決問題的工具。再如，加法模型的另一種表達，如圖2所示。

需要說明的是，模型的解釋是從抽象到具體的過程，這一過程非常重要。兒童的思維發展走向形式化并不是說要完全脫離具體，把形式化的東西具體化，把具體的東西形式化，只有當兩者均能自由實現時，才能說明學生的理解程度，這樣才能促進學生思維水平的發展，并且形式化的過程也不是一蹴而就的，而是一個反復的過程，不斷需要半抽象半具體表象支撐這一過程的發展。

（二）體驗價值，提升運用方程的內需

剛剛學習解方程，最大的矛盾是學生沒有用方程的需求，不能體會到列方程解決問題的價值。因為題目思考比較簡單，用方程要寫設未知數，書寫反而麻煩。所以，學生是排斥方程的，除非題目明確要求列方程解答之外，學生一般不選擇用方程。如何擺脫這一困境？筆者認為，要充分讓學生體會方程解決問題的思維特點，從而體現方程的實用價值。教學中要有意識地不露痕跡地引導學生用方程解決問題，有時也可以逼迫學生“就范”，主動用方程。

一是復雜問題悟關系。教學中可讓學生用方程解決一些復雜問題，從而讓學生體會到方程能達到算術方法所不能及的簡單。需要注意的是，對這樣的題目，并不是要讓學生會做，重要的是讓學生感受方程的價值，這是一種思維方式的啟迪與熏陶，讓學生體會方程在解決問題時的優勢。因此，在教學時，可以在學生一籌莫展時，出示方程，然后讓學生去悟出其中的數量關系，從而感受方程思路之簡，突出方程的價值。這可以作為一種數學欣賞、一種熏陶。

二是體會方程思維的樂趣。這種體驗不是外在的刺激，而是一種深層次的對智力活動的驚奇，進行思維的探究之旅。如特級教師任衛兵老師團隊開發的數學故事課程“方程的故事”一課，通過《丟番圖巧設未知數》的故事：丟番圖的學生帕普斯要解決問題“有四個數，把其中每三個相加，其和分別為20、22、24、27。求這四個數” 。從帕普斯設四個未知數列方程組開始，到丟番圖一反常規，只設一個未知數，最后學生受到啟發，不斷優化方法，列出更簡潔的方程。學生在活動中不斷感受到方程的魅力，感受到方程解決問題之巧妙。實踐證明，這種形式學生能在輕松的氛圍中進行高效、深入的數學思考，代數思維得以有效培養。當學生形成了運用方程的意識后，說明其代數思維有了進一步的發展。

代數思維與算術思維是兩種不同的思維方式，學習一種方式，并不意味著對另一種方式的否定。因此，教學中還需要通過比較，進一步感受兩種思維的特點，讓學生能根據現實情境選擇合適的方法解決問題。總的來說，小學生算術思維向代數思維的躍升，并非是一蹴而就的，而是連續性與非連續的結合，代數思維的可持續發展，需要學生在解決問題的過程中，提升把握關系的能力，在反思中感受方程的價值，形成結構化的思維方式。

（基金項目：本文系江蘇省“十三五”立項課題“促進理解的小學數學結構化學習的實踐研究”（編號：D/2020/02/138）的研究成果）