初中數(shù)學(xué)例題變式教學(xué)的實(shí)踐與認(rèn)識

蔣媛

【摘? 要】本文對初中數(shù)學(xué)例題變式教學(xué)的實(shí)踐進(jìn)行探究。首先，概述初中數(shù)學(xué)例題變式教學(xué)的原則，包括目的性原則、啟發(fā)性原則；其次，分析例題變式教學(xué)的作用；最后，從概念教學(xué)、習(xí)題教學(xué)、復(fù)習(xí)教學(xué)三個角度出發(fā)，列舉例題變式教學(xué)的實(shí)踐策略。

【關(guān)鍵詞】初中數(shù)學(xué)；例題變式；教學(xué)

一、初中數(shù)學(xué)例題變式教學(xué)的原則

近年來，在初中數(shù)學(xué)課堂教學(xué)中，有很多教師對例題變式教學(xué)活動進(jìn)行了一系列的探索與嘗試，取得了寶貴的經(jīng)驗(yàn)，經(jīng)驗(yàn)表明，遵循以下原則進(jìn)行例題變式教學(xué)，可使例題變式教學(xué)取得最佳成效。

（一）目的性教學(xué)原則

例題變式教學(xué)中，教師多數(shù)情況下都會使用現(xiàn)成材料進(jìn)行課堂教學(xué)，如針對教材中出示的例題，設(shè)置變式題目進(jìn)行課堂教學(xué)。教師有必要遵循目的性教學(xué)原則，完成教學(xué)工作，將現(xiàn)有的資料，以多種方式進(jìn)行靈活變化，形成更具針對性、創(chuàng)新性的例題，吸引學(xué)生的注意力。結(jié)合教學(xué)需求，采用多種新穎的教學(xué)模式，為學(xué)生講解例題及變式題，使課堂變得更豐富多彩，活躍學(xué)生的學(xué)習(xí)思維，緩解學(xué)生的學(xué)習(xí)疲勞，最大化發(fā)揮例題變式教學(xué)的效果。為達(dá)到以上教學(xué)目的，教師有必要在備課環(huán)節(jié)中，仔細(xì)分析題目特點(diǎn)，找到變式方向，如此便可使變式題教學(xué)真正成為數(shù)學(xué)教學(xué)的助推力，促進(jìn)學(xué)生的成長和發(fā)展。

（二）啟發(fā)性教學(xué)原則

以循循善誘的啟發(fā)性教學(xué)方式，引導(dǎo)學(xué)生進(jìn)行自主探究式學(xué)習(xí)，是課程改革倡導(dǎo)的教學(xué)思路。教師應(yīng)遵循啟發(fā)式教學(xué)原則，開展例題變式教學(xué)。在日常授課過程中，教師應(yīng)結(jié)合學(xué)生的學(xué)習(xí)需求、學(xué)習(xí)能力、思維特點(diǎn)甚至興趣愛好，選擇具體的例題變式教學(xué)方法，循序漸進(jìn)、潛移默化地帶領(lǐng)學(xué)生借助變式題，鞏固數(shù)形知識、技能，提升學(xué)生的學(xué)習(xí)質(zhì)量，推動學(xué)生數(shù)學(xué)學(xué)習(xí)水平的持續(xù)進(jìn)步。

二、初中數(shù)學(xué)例題變式教學(xué)的作用

（一）有利于幫助學(xué)生克服思維定勢

長期學(xué)習(xí)數(shù)學(xué)學(xué)科后，學(xué)生往往會形成一定的思維定勢，這種思維定勢通常指的是一種固化的思維習(xí)慣。大量研究及實(shí)例證明，人腦的認(rèn)識活動常受“經(jīng)驗(yàn)”的影響，有時人們會因這種經(jīng)驗(yàn)的影響而走入誤區(qū)，這便是思維定勢為人們帶來的不利影響，若無法及時察覺這種思維定勢，人們的思考會變得因循守舊、生搬硬套，細(xì)化到數(shù)學(xué)解題領(lǐng)域中，就是學(xué)生常會因思維定勢的蒙蔽，走入解題的誤區(qū)。教師可借助例題變式教學(xué)，解決以上問題，減少思維定勢為學(xué)生帶來的影響，使學(xué)生的學(xué)習(xí)思維變得更科學(xué)、嚴(yán)謹(jǐn)，鼓勵學(xué)生開闊思路，使學(xué)生逐漸形成良好的思維習(xí)慣。

（二）有利于培養(yǎng)學(xué)生的發(fā)散思維能力

培育學(xué)生的發(fā)散思維能力，使學(xué)生解題思維變得更為變通，這也有助于提升學(xué)生的數(shù)學(xué)學(xué)習(xí)水平。初中生正處青春期，大腦尚在發(fā)育，可塑性強(qiáng)，教師可借助例題變式教學(xué)，開發(fā)學(xué)生的潛能，促進(jìn)學(xué)生發(fā)散思維能力及創(chuàng)新能力的成長發(fā)展。例如，教師可從例題的情境、條件等角度出發(fā)，給予例題靈活的變化，從多視角切入，考查學(xué)生對不同知識的掌握情況，使學(xué)生形成挑戰(zhàn)欲望，激發(fā)學(xué)生的學(xué)習(xí)積極性，拓展學(xué)生的發(fā)散思維能力。此外，現(xiàn)階段看來，初中數(shù)學(xué)課堂中，進(jìn)行例題變式教學(xué)的價值，還在于能夠彰顯數(shù)學(xué)學(xué)科的本質(zhì)，能夠幫助學(xué)生更為明確地察覺題目給出的干擾項(xiàng)，對數(shù)學(xué)知識的本質(zhì)產(chǎn)生明確認(rèn)識，這同樣也有助于拓寬學(xué)生的發(fā)散思維，使學(xué)生在學(xué)習(xí)時能舉一反三、靈活變通。

三、初中數(shù)學(xué)例題變式教學(xué)的實(shí)踐策略

（一）概念教學(xué)中的變式教學(xué)

概念教學(xué)是數(shù)學(xué)教學(xué)的基礎(chǔ)。目前看來，初中課堂中，很多學(xué)生背誦數(shù)學(xué)公式十分熟練，卻對概念的理解十分膚淺，在使用這些數(shù)學(xué)基礎(chǔ)知識進(jìn)行解題時，常會遇到瓶頸，若教師給予變式題，這些學(xué)生很難順利完成“舉一反三”。為解決以上問題，使這類學(xué)生真正領(lǐng)會數(shù)學(xué)概念的核心意義，教師應(yīng)重視在概念教學(xué)中，為學(xué)生設(shè)計(jì)一系列的變式題，將概念還原到真實(shí)的數(shù)學(xué)模型或數(shù)學(xué)情境中，為學(xué)生呈現(xiàn)有針對性的變式題，供學(xué)生進(jìn)行探索，使數(shù)學(xué)概念的內(nèi)涵變得更為清晰、明確，使學(xué)生更好地經(jīng)歷知識體系在腦海中構(gòu)建而成的全過程，突破概念教學(xué)瓶頸。

以對“相似三角形”這一知識內(nèi)容的教學(xué)為例。教師可為學(xué)生出示兩個全等三角形△ABC、△DEF，并提出問題：這兩個三角形是全等三角形嗎？你是如何判斷的？你認(rèn)為滿足什么特征的兩個三角形，可被稱作全等三角形？引導(dǎo)學(xué)生對這些問題展開思索。之后教師可為學(xué)生拿出兩張大小不同的中國地圖，提問學(xué)生這兩張地圖有怎樣的關(guān)系？接著為學(xué)生展示兩個大小不同的等邊三角形，引導(dǎo)學(xué)生分析“全等三角形”的特點(diǎn)。最后，教師可為學(xué)生展示兩組相似三角形，鼓勵學(xué)生走上臺來，以直尺等工具，測量兩個三角形，分析“相似三角形”的內(nèi)涵，明確相似三角形的判斷定理，掌握概念的核心特征。

又如在教學(xué)“平面直角坐標(biāo)系”這一知識點(diǎn)時，教師可針對例題，為學(xué)生設(shè)計(jì)變式題：

（1）x軸上有一點(diǎn)P（a，b），求b的值是多少；若點(diǎn)P位于y軸上，求a的值是多少；若點(diǎn)P與0點(diǎn)重合，求a、b的值分別是多少。

（2）若點(diǎn)P位于第一象限，求a與b的取值范圍。若條件不變，P位于第三象限呢？

（3）求點(diǎn)P（-3，1）到x軸、y軸、原點(diǎn)的距離。

（4）若點(diǎn)P到x軸距離為5，到y(tǒng)軸距離為4，且點(diǎn)P位于第二象限，寫出點(diǎn)P的坐標(biāo)。

（5）已知點(diǎn)P坐標(biāo)為（3，-6），現(xiàn)有一點(diǎn)關(guān)于x軸與點(diǎn)P對稱，寫出該點(diǎn)坐標(biāo)；還有一點(diǎn)關(guān)于y軸與點(diǎn)P對稱，寫出該點(diǎn)坐標(biāo)。

教師可依據(jù)教學(xué)需求及學(xué)生的學(xué)習(xí)情況，精心設(shè)計(jì)層層遞進(jìn)、由淺入深的變式題，訓(xùn)練學(xué)生的思維，讓學(xué)生感受到通過自主探究，一步步探明數(shù)學(xué)概念的滿足感與成就感，升華學(xué)生對核心概念的理解，增強(qiáng)學(xué)生的解題能力，培育學(xué)生的思維品質(zhì)。

（二）例題教學(xué)中的變式教學(xué)

現(xiàn)階段來看，數(shù)學(xué)教材給出的例題極具典型性，對學(xué)生而言，有良好的潛能開發(fā)價值。在教學(xué)過程中，若教師僅沿用傳統(tǒng)教學(xué)手段，讓學(xué)生孤立、靜止地解答這些習(xí)題，學(xué)生獲得的學(xué)習(xí)體驗(yàn)，也僅是使用學(xué)過的數(shù)學(xué)知識，解決了一個問題而已。但如果教師能夠指引學(xué)生對例題展開深入研究，通過一題多解、一題多變等方式，挖掘題目更為深刻的學(xué)習(xí)價值，長此以往，學(xué)生思維的靈活性與深刻性將會得到質(zhì)的提升，教學(xué)成效會更加顯著。同時，在教學(xué)過程中，為學(xué)生設(shè)計(jì)恰當(dāng)合理的變式題目，也有助于在課堂中營造出民主、活躍、寬松的學(xué)習(xí)氛圍，使學(xué)生對數(shù)學(xué)知識產(chǎn)生一定的親近感，這有利于減小學(xué)生的學(xué)習(xí)壓力，培育學(xué)生的創(chuàng)新精神，使學(xué)生逐步形成從多視角出發(fā)、自主探究數(shù)學(xué)題目的意識、習(xí)慣與能力。

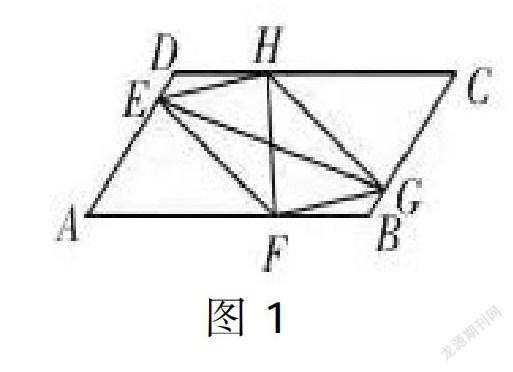
原題：如圖1所示，已知四邊形ABCD為平行四邊形，AF與CH、DE與BG長度相等，EG與HF互相平分嗎？為什么？

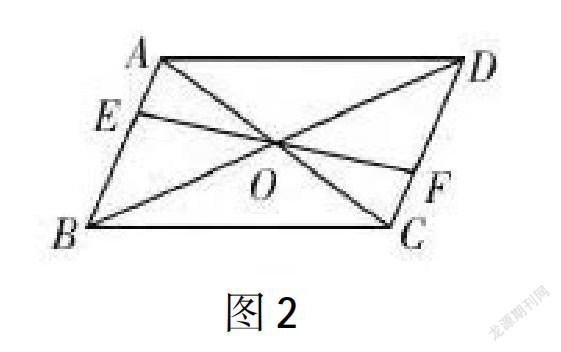
變式1：如圖2所示，已知四邊形ABCD為平行四邊形，O為對角線AC與BD的交點(diǎn)，現(xiàn)作一線過點(diǎn)O，交AB、CD于點(diǎn)E、點(diǎn)F，OE與OF長度相等嗎？為什么？

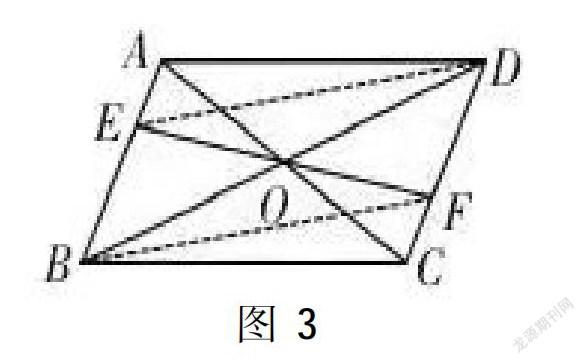
變式2：連接圖2中哪些線段，可構(gòu)成新的平行四邊形？圖3、圖4出示了兩種構(gòu)成新的平行四邊形的方法，請證明四邊形EBFD、AECF為平行四邊形。

變式3：圖2中， 若過點(diǎn)O，再作一線段GH， 分別交AD、BC于點(diǎn)G和點(diǎn)H （圖5） ， 可得到哪些新的平行四邊形，為什么？

在上題組中，教師對題目的條件、結(jié)論、背景給予了層層遞進(jìn)的變化，為學(xué)生提供了一系列豐富多樣的變式題，從不同角度出發(fā)，考查了學(xué)生對課堂所學(xué)知識的掌握情況，這有利于使學(xué)生形成靈活的數(shù)學(xué)解題思維，提升學(xué)生的學(xué)習(xí)水平。

（三）復(fù)習(xí)教學(xué)中的變式教學(xué)

復(fù)習(xí)課在初中數(shù)學(xué)課堂教學(xué)中有重要的作用。在課程改革背景下，教師應(yīng)積極思索傳統(tǒng)復(fù)習(xí)課的不足，將復(fù)習(xí)課真正視作深化、提升學(xué)生學(xué)習(xí)思維的重要環(huán)節(jié)，精選習(xí)題，給予學(xué)生有針對性的變式訓(xùn)練，指導(dǎo)學(xué)生從更高層次出發(fā)，進(jìn)一步思索自己學(xué)過的數(shù)學(xué)知識，夯實(shí)知識、技能儲備。

例如在教學(xué)完“全等三角形”一課后，教師可為學(xué)生設(shè)計(jì)變式題：

問題：在△ABC中，有AB=AC，BD與CE為三角形角平分線，求證BD=CE。

教師可設(shè)計(jì)以下的變式題：（1）你能夠用不同方法證明BD=CE嗎？（2）原題目中，若已知條件不變，可得出哪些結(jié)論？（3）能否在改變已知條件的情況下，證得BD=CE？（4）請你同時改變已知條件與結(jié)論，甚至改變圖形，利用學(xué)過的知識點(diǎn)，對題目進(jìn)行一定的改編，并自己回答問題。

以上的變式題，體現(xiàn)了教師與學(xué)生對“全等三角形”相關(guān)題目的創(chuàng)新，實(shí)踐證明有良好的課堂教學(xué)效果。在數(shù)學(xué)課堂教學(xué)中，教師應(yīng)重視革新問題情境與問題條件，使題目變得更為新穎，培養(yǎng)學(xué)生“舉一反三”的思維習(xí)慣。但應(yīng)注意，為“變式”而“變式”，設(shè)計(jì)形式僵化的數(shù)學(xué)題也是不妥當(dāng)?shù)模處煈?yīng)遵循目的性原則，結(jié)合教學(xué)目標(biāo)設(shè)計(jì)變式題，確保變式題與學(xué)生的學(xué)習(xí)需求一致，力求激發(fā)學(xué)生思維的積極性與創(chuàng)造性，使學(xué)生活學(xué)活用、學(xué)以致用地學(xué)習(xí)數(shù)學(xué)知識，彰顯數(shù)學(xué)知識的本質(zhì)屬性，培養(yǎng)學(xué)生的知識應(yīng)用能力、發(fā)散思維能力與創(chuàng)新能力，促進(jìn)學(xué)生的進(jìn)步發(fā)展。

四、結(jié)束語

綜上所述，在初中數(shù)學(xué)課堂教學(xué)中，圍繞教材給出的例題，為學(xué)生設(shè)計(jì)一系列的變式題目，有重要的意義。教師應(yīng)為例題變式教學(xué)制訂明確的目標(biāo)，結(jié)合學(xué)生的學(xué)習(xí)基礎(chǔ)、學(xué)習(xí)需求，圍繞例題，給予學(xué)生一系列層層遞進(jìn)的變式題目，發(fā)展學(xué)生的數(shù)學(xué)思維能力，促進(jìn)學(xué)生的持續(xù)成長。

【參考文獻(xiàn)】

[1]許道娒.“變式教學(xué)活動”在初中數(shù)學(xué)例題教學(xué)中的組織設(shè)計(jì)[J].教育界，2020（27）：50-51.

[2]胡安紅.初中數(shù)學(xué)教學(xué)中變式題的應(yīng)用技巧探究[J].新智慧，2019（3）：32.

[3]吳玉龍.掌握初中數(shù)學(xué)變式題組，提升復(fù)習(xí)課學(xué)習(xí)效果[J].現(xiàn)代中學(xué)生（初中版），2021（6）：25-26.