自尋優最大轉矩電流比矢量控制連載之三：同步磁阻電機電感掃描的虛擬信號注入法控制

張雨馨，王云沖,2，史 丹，徐彬涵，沈建新,3

(1.浙江大學 電氣工程學院，杭州 310027；2.浙江省電機系統智能控制與變流技術重點實驗室，杭州 310027；3.流體動力與機電系統國家重點實驗室，杭州 310027)

0 引 言

針對同步磁阻電機(以下簡稱SynRM)的最大轉矩電流比(以下簡稱MTPA)控制，學者們提出了多種虛擬信號注入法(以下簡稱VSIM)[1-7]。信號注入法通過注入前后的轉矩值來提取判定MTPA點的信息。真實的信號注入法[8]可通過測量獲取注入前后的轉矩值，而VSIM不具備此測量條件。VSIM的解決方案是構建注入信號后的轉矩數學模型，通過近似計算來獲得注入后的轉矩數據。VSIM沒有真正注入信號，不會造成額外損耗，同時保留真實信號注入法計算方便、動態響應快的優點。

VSIM常用的虛擬注入信號有正弦波[1-2]和方波[3]。采用虛擬正弦波信號注入法的控制模塊涉及大量信號處理環節，引入較多濾波器，算法動態性能較差，而采用虛擬方波信號注入法可以解決這些問題。同時文獻[3]修正了虛擬注入控制法的方程，引入了與d軸電感參數有關的補償項，提高了算法的穩態精度。該算法將此補償項中的d軸電感參數視為常數，取空載下的d軸電感為近似。然而SynRM參數是非線性變化的，當電機進入飽和區工作時算法的穩態控制精度會下降。

考慮到SynRM參數非線性變化的特性，本文采用引入補償項的轉矩模型，將其中d軸電感參數作為優化搜索變量，獲得考慮電機參數非線性的精準轉矩模型，在此模型上進行虛擬雙極性方波信號注入MTPA尋優，可以有效補償電機參數非線性變化帶來的誤差，取得較好的MTPA控制效果。該方法可以避免如傳統搜索法直接對電流矢量角進行高時間成本的搜索，在虛擬信號注入法的基礎上對電感參數進行掃描，間接實現極值搜索，具有更高的控制精度和動態特性。

1 SynRM模型

三相SynRM在d-q參考坐標系下的模型可以表述：

(1)

(2)

(3)

(4)

iq=Iscosβ

(5)

id=-Issinβ

(6)

式中：vd,vq分別為d,q軸電壓；id,iq分別為d,q軸定子電流；Ld,Lq分別為d,q軸電感；R為定子電阻；Te,TL分別為電磁轉矩和負載轉矩；ωm為轉子的機械角速度；p為電機極對數；Bm為摩擦系數；J為轉動慣量；Is為電流矢量的幅值；β為電流矢量超前q軸的相位角。

SynRM轉子沒有永磁體，從式(3)可以看出，其轉矩主要為d,q軸電感差導致的磁阻轉矩。運行過程中電機的磁路會隨著定子電流的變化發生非線性的飽和，同時受到交叉耦合的影響，d,q軸電感隨著d,q軸電流的變化而變化。因此SynRM參數具有顯著的非線性變化特性，在控制過程中不可忽略。

針對SynRM MTPA控制，傳統的45°電流相位角公式法在控制過程中將電機電感參數視為常數，忽略參數的非線性變化，難以實現準確的MTPA控制。電機參數的非線性變化難以用模型準確擬合，故LUT和在線參數辨識法需要進行復雜的工作且難以實現精準的控制。為考慮SynRM參數非線性特性，同時不依賴參數，學者們提出搜索法來實現精準的MTPA控制。

2 基于電流相位角搜索的MTPA控制原理

2.1 電流相位角極值搜索原理

搜索法將電機系統看作一個黑箱，不考慮具體的電機模型及參數，其核心是以電流相位角為優化變量，以最小化電流幅值為優化目標，通過不斷檢索尋優找到使電流幅值最小化的MTPA點。具體可通過向電流相位角施加一定擾動信號，根據反饋回來的電流幅值的變化情況，在線搜索對應于電流最小時的MTPA點。不同的擾動信號、搜索方式對應不同的控制精度，下面以正弦式擾動為例描述電流相位角極值搜索原理。電流相位角擾動調制方式的數學描述：

(7)

式中：β為電機穩態運行時的電流相位角；k1為相位角變化方向，取+1或者-1；k2為相位角調制的幅度；ti為控制周期中的采樣時間。

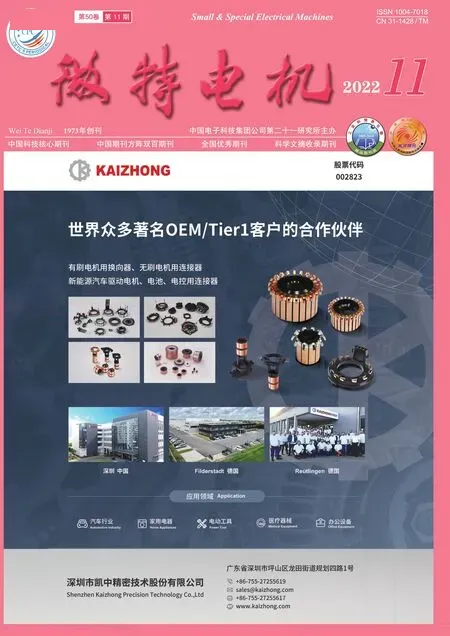
電流相位角的擾動會引起電流幅值的變化ΔIs,常用的判斷方式為閾值三段式，需提前預設一個閾值ΔI閾。

1) ΔIs小于-ΔI閾，說明當前工作點下相位角的調整可以有效降低電流大小，維持相位角變化方向k1不變，同時更新相位角：

βbase,new=βbase,old+k1k2

(8)

2) ΔIs大于ΔI閾，說明當前工作點下相位角的調整反而導致電機電流增大，需要改變相位角變化方向，對k1取反，同時如式(8)更新相位角。

3) ΔIs絕對值小于ΔI閾，說明當前工作點下相位角的變動對電流基本沒有優化效果，可認為當前的工作點已處于最佳位置，只需維持此相位角不變即可。

以上三種情形電流相位角β的變化如圖1所示。

圖1 相位角極值搜索法的閾值三段式控制

圖1中的正弦波動表示搜索過程中對電流相位角的擾動，根據閾值三段式的判斷，對相位角進行相應的調整，可以使得電機最終穩定工作在最優MTPA點。

2.2 基于極值搜索原理的VSIM

極值搜索法直接將電流相位角作為搜索變量進行工作點尋優，以相位角施加擾動后電流幅值的變化為控制依據，不依賴參數便可實現最優MTPA控制，然而極值搜索法動態性能較差。基于極值搜索法的原理，學者們提出信號注入法，改善了算法的動態性能。信號注入法向系統中注入小信號來提取判斷電機是否工作在MTPA的信息。真實注入信號會引入額外損耗，造成轉矩波動等，VSIM注入虛擬的信號，克服了真實信號注入法的缺點。虛擬單極性方波注入法便屬于VSIM的一種。

虛擬單極性方波注入法采用占空比為50%的方波作為虛擬信號：

(9)

式中：N=1,2,3…；δ和Ts分別表示方波信號的幅值和周期。

對注入虛擬方波信號后的轉矩進行泰勒展開及忽略二階及以上導數項，可得：

(10)

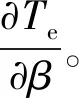
(11)

式中：Ld的值采用空載下的Ld值做近似。

根據前述對SynRM模型的分析，電機的電感參數是非線性變化的，將其視為常數則將降低MTPA尋優的準確性。實際上每一個電感值Ld均對應了一個虛擬信號注入法的參考轉矩模型，結合極值搜索法的原理，可將Ld看成類似電流相位角的一種決定控制系統性能的參數，通過檢索Ld以決定最佳參考轉矩數學模型。最佳工作相位角再經由最佳參考轉矩模型進行虛擬信號注入法尋跡得到。

本文基于虛擬雙極性信號注入法系統，通過掃描搜索最優的電感參數Ld，并以式(11)重建轉矩模型，從而間接實現極值搜索，這種方式結合了傳統VSIM動態響應快速的優點，可避免直接對電流相位角進行搜索造成的高時間成本。

3 電感參數掃描MTPA控制算法

3.1 電感參數掃描MTPA基本原理

考慮到MTPA的控制目標為最小化給定轉矩下所需的電流，電機的實際電流值可以通過電流傳感器直接觀測，因此基于VSIM的電感參數掃描法以電流矢量幅值作為監控目標，通過記錄每一輪電感值掃描變化后的電流幅值，以決定適配當前工況的最佳電感值，并以此電感值作為當下VSIM中重建轉矩模型里的電感值Ld。

具體控制思路：首先，基于當前電感值的轉矩模型，采用VSIM控制電機，記錄電機的穩態電流值。然后對電感施加小偏移量，VSIM根據更新后的電感值再次尋優相位角。在算法穩定之后，記錄下新穩態下的電流值。通過比較兩次穩態的電流值可以判斷電感值修正產生的是正向作用還是反向作用，從而決定下一次電感值的修正方向。其工作原理如圖2所示，圖2中θ為由于電機的機電常數而產生的時延值。

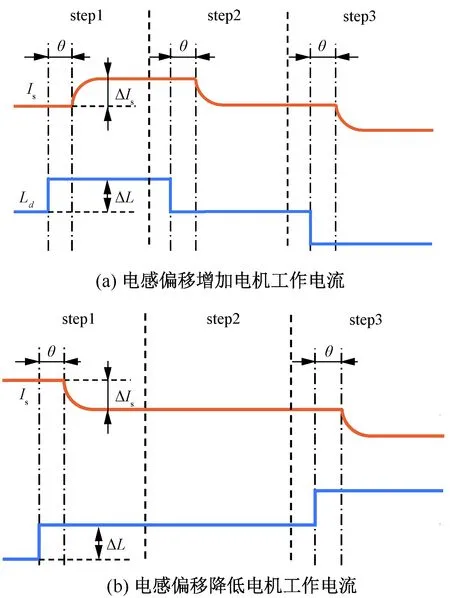
圖2 電感參數掃描法原理圖

圖2中，電感參數掃描可以分為兩種情況處理：

1) 如圖2(a)所示，電機在新穩態下的電流值比之前值更大，需改變電感掃描的方向，并舍棄此時的電感值，沿用之前的電感作為電感基值；

2) 如圖2(b)所示，電感值偏移后，電機在新穩態下的電流值比之前值更小，說明此時更新的電感值更加逼近最佳電感。維持電感掃描的方向，且將偏移后的電感值更新為新的電感基值。

圖3展示了電感參數掃描法控制下電機工作點在轉矩曲線上的變化過程。實線為考慮參數非線性變化特性的SynRM的真實轉矩曲線，虛線為采用不同電感值對應的參考轉矩模型。電感掃描法迭代更新電感值來修正參考轉矩模型，此過程以實線箭頭指示在圖3中。可以看到，電機經過不斷迭代，最終能夠穩定工作在MTPA點，實現良好的控制效果。

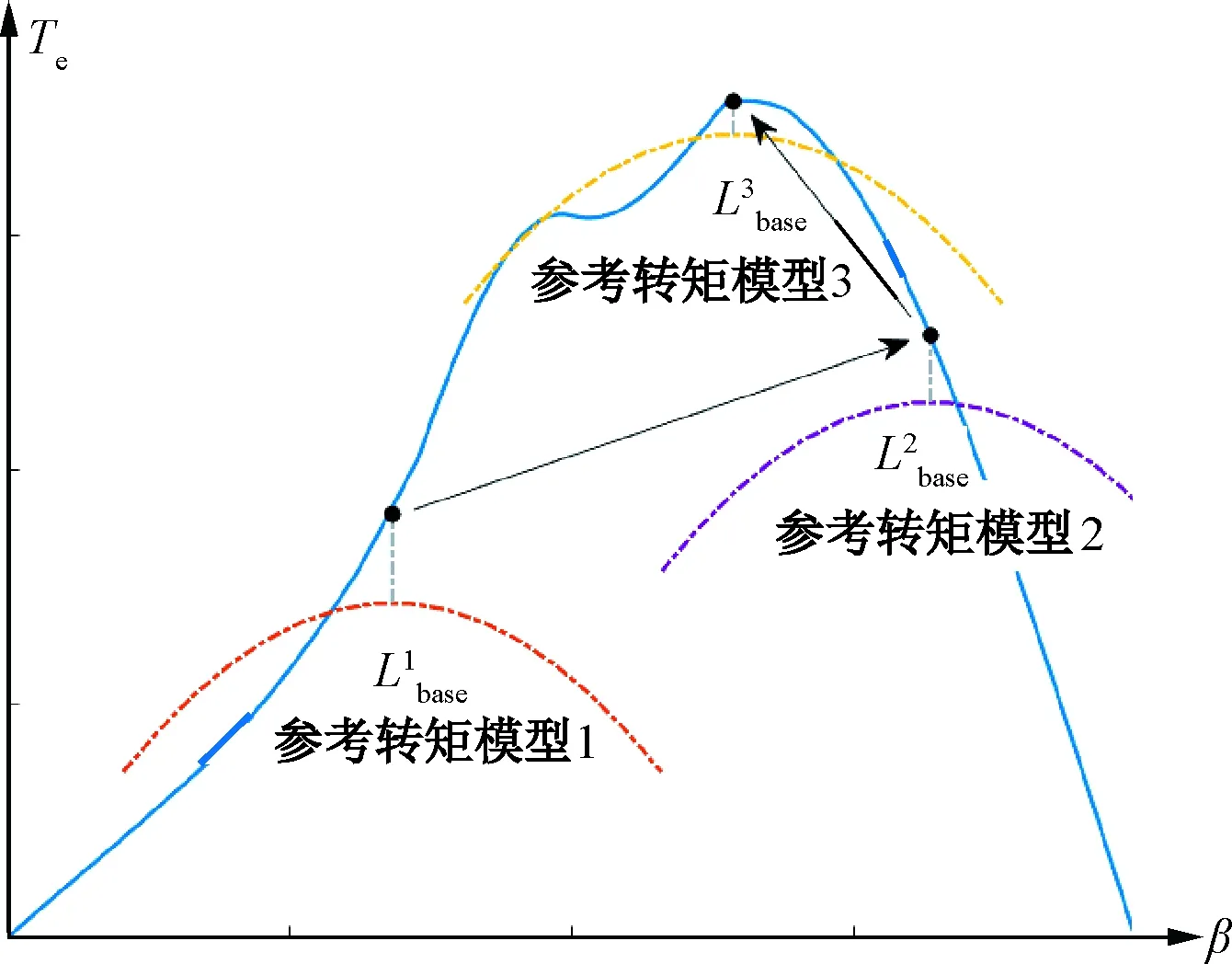
圖3 電感參數掃描法控制過程

3.2 雙向增量電感探測機制

合理搜索步幅能較大提高搜索法的控制效率。電流相位角極值搜索法采用的傳統閾值三段式法的步長是固定的，無法依據與最佳點間的距離和電機參數范圍進行靈活調整，且閾值設計的精準度會影響判斷工況變化的靈敏度。本文設計雙向增量電感探測機制，可以同時確定電感值變化的方向和步長，根據控制效果和工況進行靈活調節。

雙向電感探測機制設計如下：

1) 基于當前電感值的參考轉矩模型進行VSIM控制，當電機運行到穩態時記錄當前的電流值Io；

2) 令Ld正向偏移ΔL，基于新的電感值運行VSIM直至穩定，記錄此時的電流值Ipos；

3) 令Ld負向偏移ΔL，同樣記錄系統穩定后電流值Ineg；

4) 通過比較Ipos和Ineg來修正Ld，更新公式：

Lbase,new=Lbase,old-k(Ipos-Ineg)

(12)

式中：k為電感更新系數。

5) 重復上述步驟至電流穩定趨向定值。

ΔL被稱為探測電感，其值相對而言比較小，這樣設計的目的在于令系統穩定時不會引起大的模型振蕩而導致電流中出現較大的紋波。雙向增量電感探測機制的邏輯原理如圖4所示。

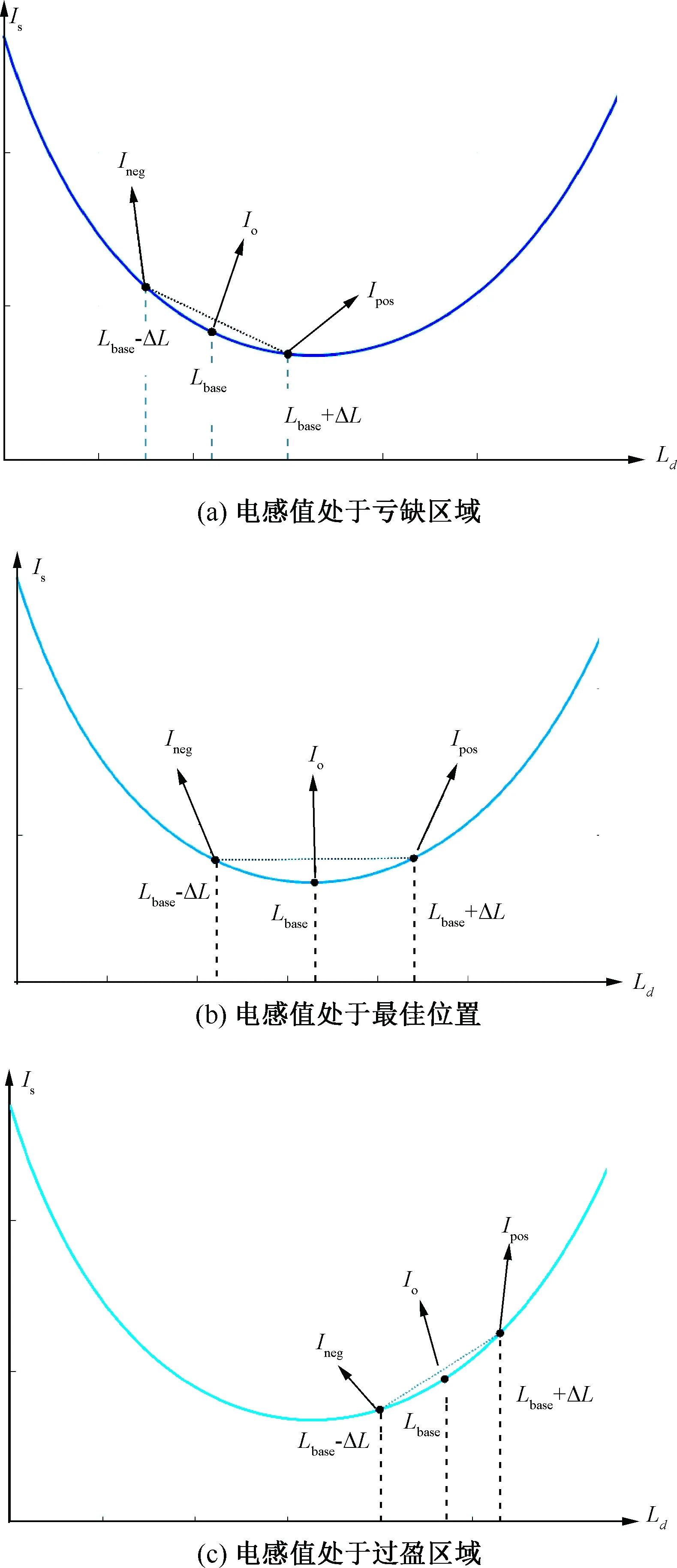
圖4 雙向增量電感探測機制原理

圖4(b)中，當正向探測結果和反向探測結果橫跨在極值點的兩端時，當前的電感能穩定落在最佳電感值處，實現最優MTPA控制。此外，電感的更新步幅與正向探測和反向探測得到的電流差值線性相關，故算法在不同電機模型和工況變動中均能自適應調整電感參數掃描步幅直至穩定，實現高性能控制。

4 仿真分析

首先對電感參數掃描法進行理論仿真。在Simulink中搭建的SynRM模型的電感參數是非線性變化的，與被控制電機的有限元仿真結果一致，在控制過程中通過查表獲得。電機參數如表1所示。

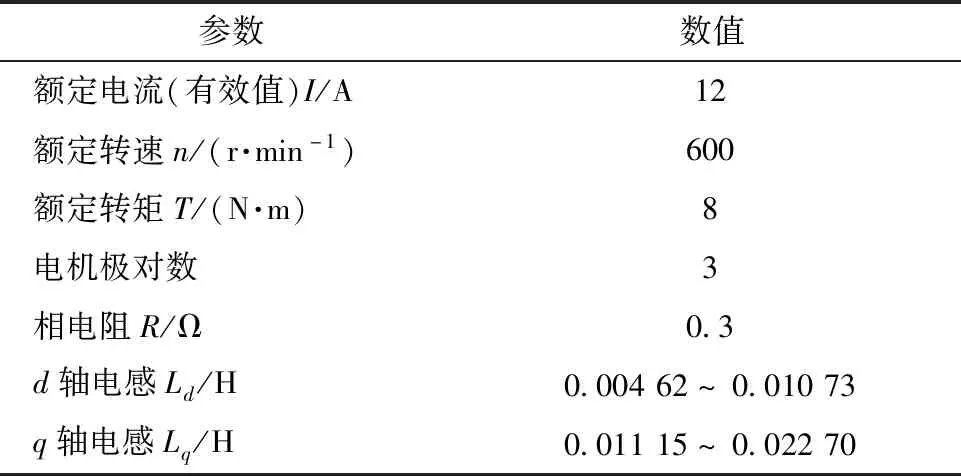
表1 SynRM參數

4.1 穩態性能研究

將仿真得到的電感參數掃描法與傳統的虛擬單極性方波信號注入法控制下的電機穩態電流幅值的結果進行對比，如表2所示。仿真中給定負載轉矩分別為2 N·m、4 N·m、6 N·m、8 N·m，給定轉速為600 r/min。

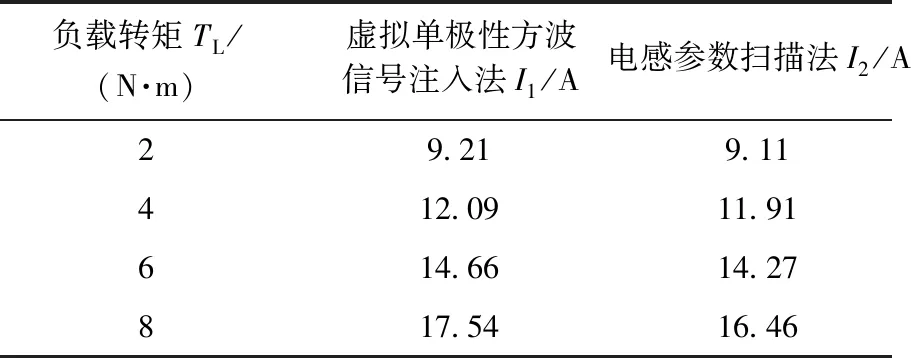
表2 600 r/min下SynRM穩態電流值仿真結果

從表2中可以看出，考慮了SynRM非線性特性的電感參數掃描法具有更高的穩態精度，較大地減小了電機穩態電流幅值，能有效降低電機損耗，提升電機效率。

4.2 暫態性能研究

在給定轉速為600 r/min，給定負載轉矩在t=2.5 s時刻由2 N·m突變至6 N·m工況下，觀察電機在電感參數掃描法控制下電流幅值、電流矢量相位角的變化，并將結果與虛擬方波信號注入法的暫態響應結果作比對。

圖5展示了兩種MTPA方法控制下電機電流幅值Is的暫態波形。可以看到，由于電感參數掃描法考慮了電機參數非線性特性，對電感參數進行極值搜索，搜尋最優電感值，相比于虛擬單極性方波注入法有了較大的提升，其控制下的電機電流幅值比虛擬單極性方波注入法小，并且隨著轉矩的增大，算法的優化效果更顯著。

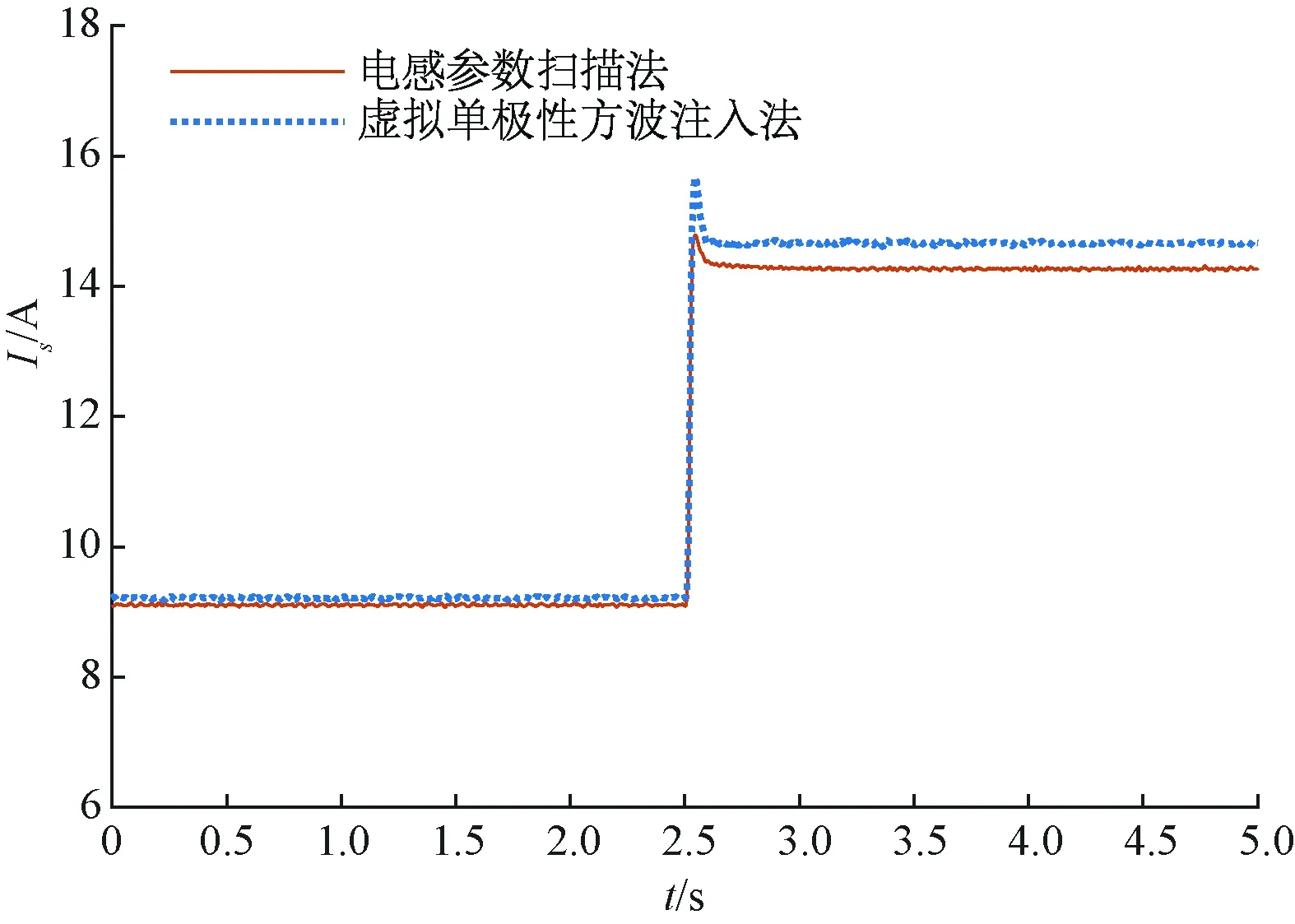
圖5 600 r/min變負載下的電流幅值波形

圖6展示在兩種MTPA控制方法下電機電流矢量相位角β的暫態響應波形。可以看出，負載突變后，本算法的電流相位角經一段時間后基本進入穩定，但由于采用雙向增量探測機制，電機的電流矢量相位角會小幅振蕩。結合圖5可以看出，相位角的小幅振蕩并不影響電流幅值的穩定性，依然可以實現穩定且精準的MTPA控制。

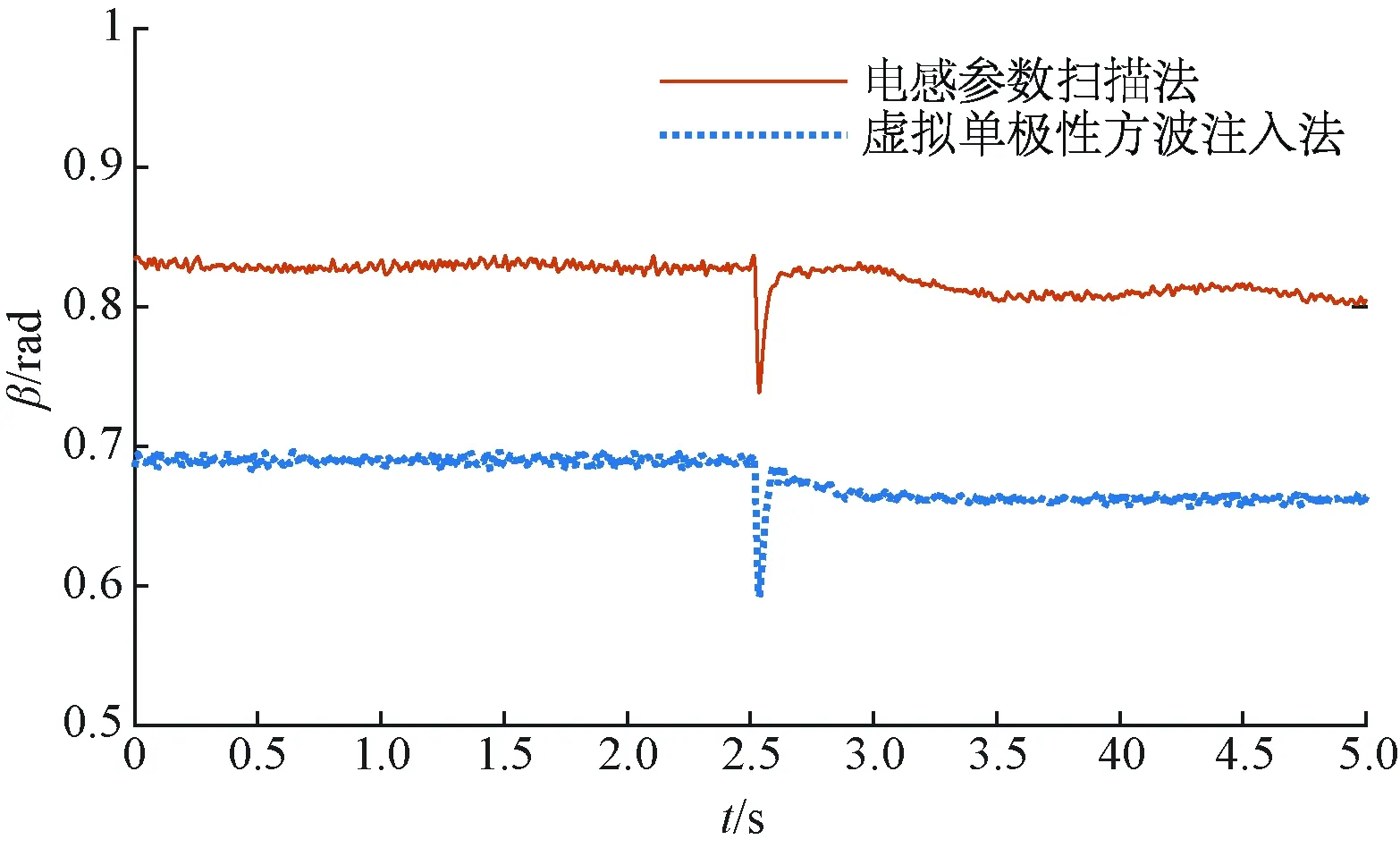
圖6 600 r/min變負載下的電流相位角波形

此外，圖7展示了本方法控制下電機d，q軸電流id,iq的暫態響應過程。事實上，從圖5的電流幅值Is和圖6的電流相位角β可以直接推導出id與iq(見式(5)和式(6))。雖然β有小幅變化，但經三角函數運算后，id與iq基本穩定。從圖7中可以看出，在負載突變的工況下，id與iq能實現快速響應，具有良好的動態性能。

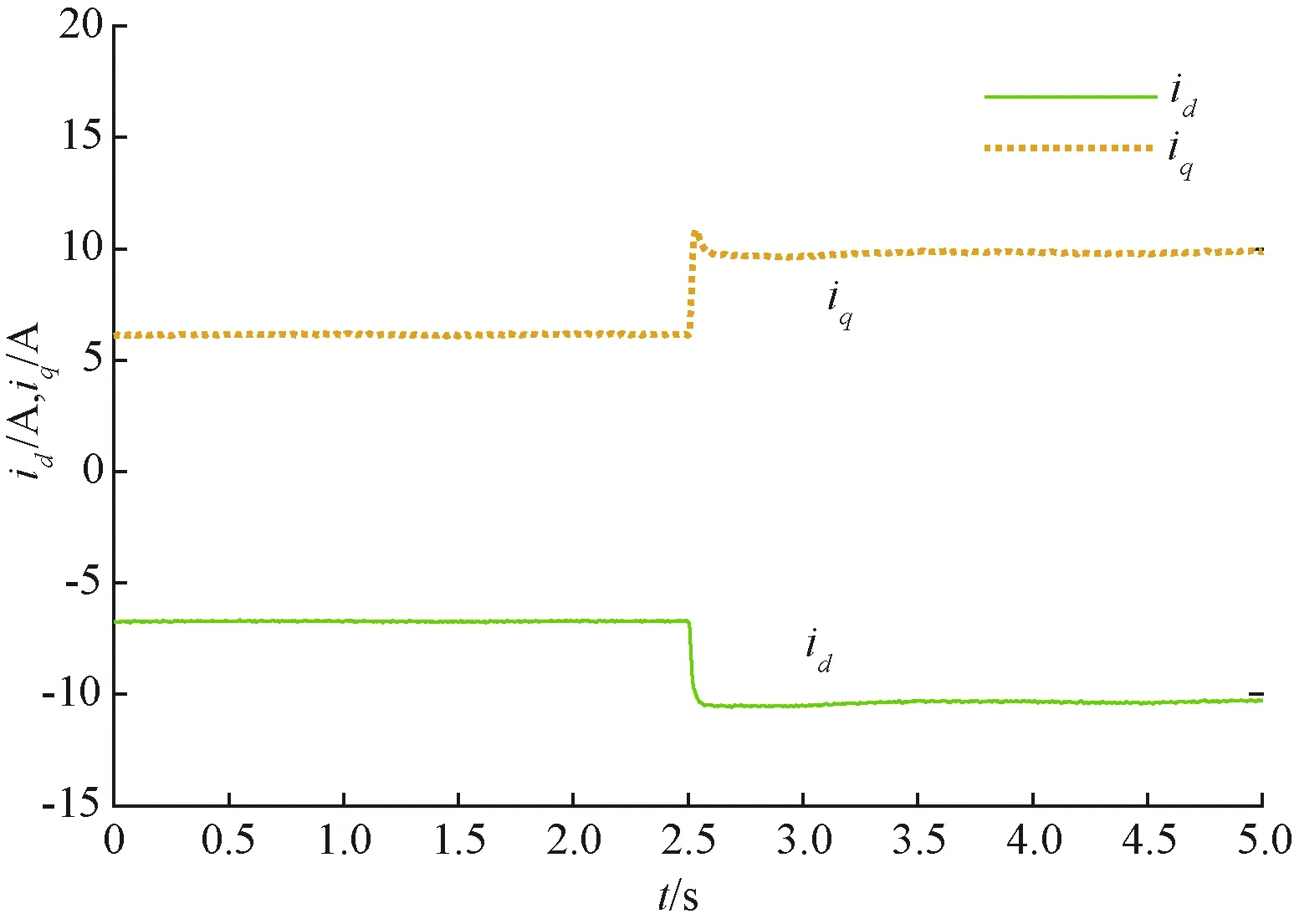
圖7 600 r/min變負載下的id,iq波形

5 實驗驗證

本文搭建了SynRM實驗臺架，對電感參數掃描法的控制性能進行實驗驗證。臺架主要由被控SynRM和作為對拖負載的PMSM組成，兩臺電機經扭矩傳感器連接。PMSM輸出的三相電流經整流橋連至電子負載，通過電子負載調整負載的大小。SynRM由Myway系統控制，Myway系統主要由SiC逆變器和PE-Expert4控制器組成，PE-Expert4搭載了處理數字信號的DSP (TMS320C6657)高性能控制板。逆變器直流側施加300 V母線電壓，被控SynRM的相關參數如表1所示。

5.1 穩態性能研究

在給定電機轉速600 r/min，負載轉矩分別為2 N·m、4 N·m、6 N·m、8 N·m四種工況下，觀測參數掃描法控制下SynRM的穩態電流幅值，并且與傳統虛擬單極性方波注入法控制下的結果作比較，如表3所示。

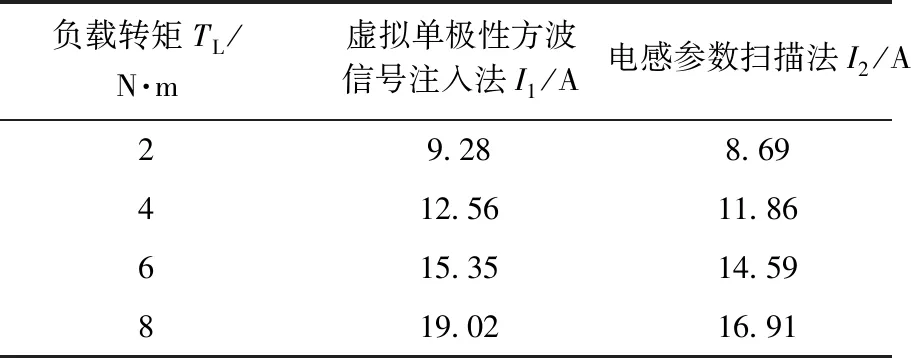
表3 600 r/min下SynRM穩態電流值實驗結果

從表3中可以看出，由于電感參數掃描法考慮了參數的非線性變化，以電感為優化變量進行極值搜索，彌補了將電機電感參數視為常數的傳統VSIM帶來的誤差，實現精準的MTPA控制，在同樣的工況下較大程度地減小了電機的電流幅值，降低了損耗，提高了電機效率。

圖8 SynRM三相電流給定量波形

實驗中，當電機穩定運行在600 r/min、8 N·m負載下時，觀測三相電流給定量，如圖8所示。可以看到電機三相波形是光滑的正弦波，這是因為：電感參數掃描法基于VSIM對電感參數進行極值搜索，不會真正注入電流矢量相位角偏移信號，不會引入額外的損耗和諧波，克服了真實信號注入法的缺陷；雖然尋優后的電流矢量相位角β有小量振蕩(見圖6)，但是d、q軸電流仍然是比較穩定的(見圖7)。β的小幅振蕩對電流波形質量沒有明顯影響。

5.2 暫態性能研究

電機給定轉速為600 r/min，觀察當負載轉矩在t=2.5 s時刻從2 N·m突變至6 N·m時電機的電流幅值與電流矢量相位角的暫態波形圖。

圖9展示了采用電感參數掃描法和虛擬單極性方波信號注入法控制下電機電流幅值Is的暫態響應波形。可以看到，相比于虛擬單極性方波信號注入法，本算法控制下的電機電流幅值大幅減小，并且在重載工況下算法的改善效果更明顯。在負載突變后，電流幅值波形能快速響應，具有良好的動態響應特性。

圖9 600 r/min變負載下的電流幅值波形

在負載突變后的2.5 s內，由于工況突變使得轉矩模型中掃描電感變化劇烈，導致這段時間內的電流幅值存在波動。但隨著電機運行狀態進入穩定，電感參數趨于穩定，此時電流幅值波形呈現較好的穩定性，也印證了圖8中電機穩態三相對稱正弦波電流波形。

圖10展示了采用電感參數掃描法和虛擬單極性方波信號注入法兩種MTPA控制方法下電機電流矢量相位角β的暫態響應波形。可以看到，由于本算法基于雙向增量探測機制對電流矢量相位角進行極值搜索，電機的電流矢量相位角存在小幅振蕩，但這并不影響圖9中電流幅值的平穩性，算法依然能實現精準穩定的MTPA控制。

圖10 600 r/min變負載下的電流相位角波形

仿真和硬件實驗的結果保持了較好的一致性，結合它們的結果可以看出，相比于虛擬方波信號注入法，電感參數掃描法能夠實現精準的MTPA控制，具有較高的穩態精度。盡管采用雙向增量電感探測極值，優化了搜索法動態響應慢的缺點，但對電感參數的檢索依然需要花費一定時間并且存在小幅振蕩。相比虛擬方波信號注入法，電感參數掃描法的動態響應特性較差，其犧牲了部分動態響應性能來提高MTPA的穩態控制精度，因此不適用于工況變化頻繁的場合。

6 結 語

本文在虛擬雙極性信號注入法的基礎上提出了電感參數掃描MTPA控制算法。考慮到SynRM電機參數非線性變化顯著，本文通過掃描搜索最優的d軸電感參數變量重建轉矩模型，間接實現極值搜索，該方法同時結合了極值搜索法不依賴參數、計算簡便和VSIM響應快速的優點，能夠實現更精準的MTPA控制。針對搜索方向和步長的設計，本文提出了雙向增量電感探測機制，可以自適應調整電感參數值增量的方向和步長，提高搜索的效率和穩定性。最后通過仿真和實驗驗證了電感參數掃描法的MTPA穩態尋優精度優于傳統的虛擬方波信號注入法，并且具有較好的動態響應特性。

該方法的缺點是，電感參數遍歷掃描的執行比較繁瑣，所花費的尋優時間較長，并且在穩態MTPA控制時電流相位角仍有小幅振蕩，當然，該振蕩對系統穩定性的影響很小。為了克服此缺點，可以采用其他方法獲得最優的電感參數，如同構電感法，將在后續論文中介紹。