聯想開路，化生為熟，提升數學運算素養

324000 浙江省衢州第二中學 汪耀生

324200 浙江省衢州數字工業學校 徐春紅

311121 浙江省杭州二中未來科技城學校 李 盛

數學運算素養是高中數學的六大核心素養之一，具體是指在明晰運算對象的基礎上，依據運算法則解決數學問題的素養.如何提升高中學生的數學運算素養，提高數學運算能力？這是高中數學教學中的一個核心問題.筆者在長期的教學實踐中發現，采用“聯想開路，化生為熟”的解題策略，對復雜的數學問題進行簡單表征，容易抓住數學問題的本質，把握研究對象的數學特征，形成解決問題的思路，使運算過程簡潔明快，解題思維程序化，感悟通性通法中的數學原理和其中蘊含的數學思想，有利于培育學生的數學運算素養.

一、聯想與轉化

聯想思維是指在人腦內記憶表象系統中，由于某種誘因使不同表象發生聯系的一種思維活動.聯想思維是很重要的一種創新思維方法，在人的思維活動中起著基礎性的作用.

轉化與化歸思想就是在研究和解決有關數學問題時，通過變換將問題轉化，進而使問題得到解決的一種數學思想方法.化陌生為熟悉是一種重要的解題策略.

當面臨一道沒有接觸過的陌生題目時，要聯想曾經解過的或比較熟悉的題目，或聯想類似題的求解方法，“化生為熟”，充分利用已有的知識、經驗或解題模式，這樣才能順利地解題.

二、應用舉例

(一)聯想熟悉的數學知識

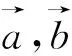
分析：聯想到絕對值的一個基本性質|a+b|+|a-b|=2max{|a|,|b|}，可簡捷求解.

例2已知數列{an}(n∈N*)滿足an+1=|a2-a1|+|a3-a2|+…+|an-an-1|(n≥2)，且a1=1，a2=a(a>1)，則a1+a2+a3+…+a24=________.(結果用含a的式子表示)

分析：題設中的關系式是若干項求和的形式，相似聯想，容易想到數列中前n項和與通項的關系，打開了解題思路.

解：當n=2時，a3=|a2-a1|=a-1.

當n≥3時，由題設得

評析：相似聯想是由某一事物或現象聯想到與它相似的其他事物或現象，進而產生某種新設想的聯想方法.解答本題時，在理解題目蘊含的信息后，通過對題目結構等信息的加工，聯想相似的數學對象和關系結構，遷移方法后發現解題思路，順利解決問題.

解決相似問題的過程中讓學生感悟數學的通性通法.對運算問題，合理選擇運算方法，設計運算程序，在演繹推理運算解決問題的過程中，學生形成規范化思考問題的品質.

(二)聯想熟悉的解題方法

例4(2021全國高中數學聯賽福建賽區預賽-7) 設正實數x,y滿足x(x+2y)=9,求x5y的最大值.

分析：聯想到這類問題的一般解題方法，利用平均值不等式，適當配湊即可解決問題.

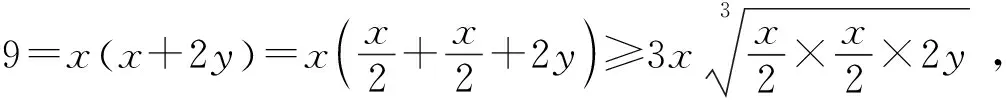
評析：這里運用的是連續性聯想思維.其主要特征是由此及彼，連綿不斷地進行，可以是直接的，也可以迂回曲折地形成閃電般的聯想鏈，連續性聯想思維是打開沉睡在頭腦深處記憶的最簡便和最適宜的鑰匙.

(三)聯想熟悉的數學問題

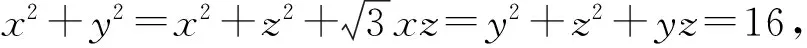
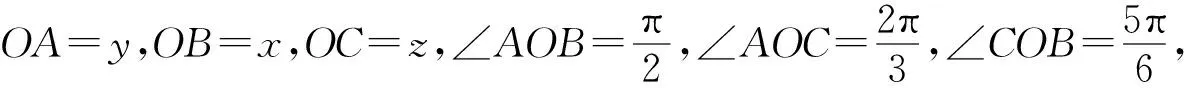
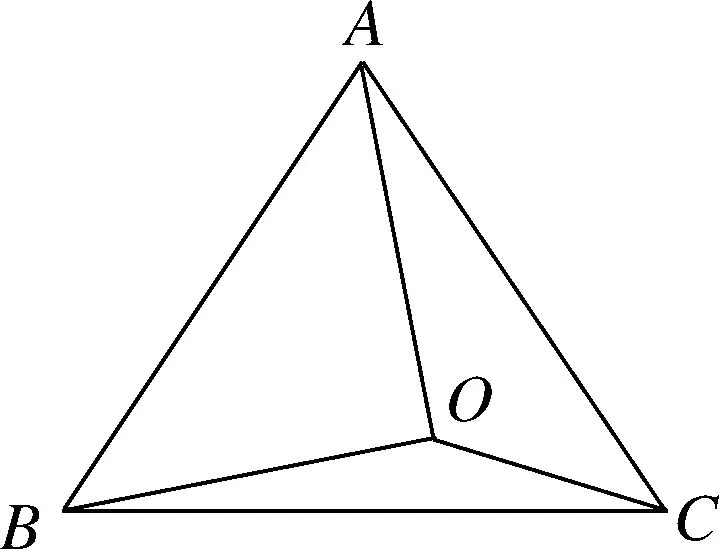
圖1

評注：根據題目條件結構，構造圖形探索解決問題的思路，“化生為熟”，尋找原型，這是破解難題的重要策略，有利于學生形成數形結合的思想.在解決某個新問題之前，如果能先知道其原型，借助圖形性質探索數學規律，研究圖形與圖形、圖形與數量之間關系的基本方法，那么對新問題的理解就會更自然、深刻和全面.遇新思陳、推陳出新對順利解決數學問題具有重要的現實意義.

例6若f(x)=(x+a)(|x-a|+|x-4|)的圖像是中心對稱圖形，則a=________.

分析：聯想已學過的中心對稱圖形，奇函數的圖像是符合要求的.已知f(x)的圖像是中心對稱圖形，若能經過適當平移，使函數f(x+t)剛巧為奇函數，則問題就能得到順利解決.

解法1：f(x-a)=x(|x-2a|+|x-4-a|)，使函數f(x-a)是奇函數，只須g(x)=|x-2a|+|x-4-a|是偶函數.

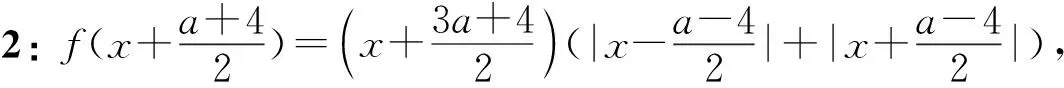
評析：聯想思維是形象思維的具體化，其基本的思維操作單元是表象，所以，聯想思維十分生動，具有鮮明的形象.

(四)變換條件，聯想熟悉的特殊技巧

變換條件，聯想熟悉的局部(或整體)處理技巧解答問題.

如果用構造函數的方法分類求導進行求解，過程比較復雜.聯想到不等式的基本性質，巧妙地對問題進行整體處理，可避免繁復的分類討論.

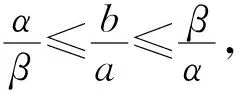
評析：聯想思維的主要特征是由此及彼，連綿不斷，或直接或迂回曲折地形成閃電般的聯想鏈，進而解決問題.

(五)類比結構，利用接近聯想轉化問題

接近聯想是根據事物之間在空間或時間上的接近進行聯想，進而產生某種新設想的思維方式.有些問題給出的結構與某些三角公式的結構完全相同，利用接近聯想，可以通過三角代換實現問題的轉化，化為三角問題.

分析：從結論x2+y2知本題求解的關鍵，是怎樣將欲求結論變換為易于應用的求解條件.

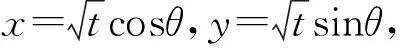
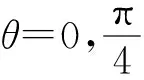
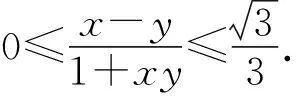
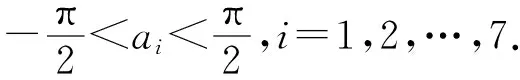
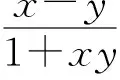
一般來說，對于題目的熟悉程度取決于對題目自身結構的認識和理解.從結構上來分析，任何一道題都包含條件和結論(或問題)兩個方面.要把陌生題轉化為熟悉題，就要根據題型全方位、多角度分析題意，充分聯想回憶基本知識和基本方法，或恰當構造輔助元素，在變換題目的條件、結論(或問題)以及它們的聯系方式上多下功夫.