基于雙流降維EEMD-CNN滾動軸承故障診斷
郭梓良, 郝如江, 王一帆, 楊文哲, 趙瑞祥
(石家莊鐵道大學機械工程學院,河北 石家莊 050043)
對工作中的軸承進行故障識別與診斷的過程中,常常受到噪聲的干擾導致故障識別準確率降低。因此對噪聲進行篩選和處理,是滾動軸承故障識別的關鍵所在[1]。
當今的軸承故障診斷主要是圍繞著故障振動信號的特征提取和分類等方面進行研究。史東海等[2]通過使用傳統方法對信號進行處理后使用PCA降維,隨后采用K近鄰算法對結果進行分類。姚峰林等[3]通過使用小波包變換對滾動軸承數據消噪處理后再進行極限學習機特征提取分類。汪朝海等[4]對原數據通過經驗模態分解后使用卷積神經網絡進行故障分類。上述方法對原始故障信號進行相應處理,削弱了噪聲干擾信號所帶來的影響,從而使得信號特征更易提取,但是仍存在著一定的不足。傳統方法雖然能減少噪聲帶來的信號干擾,但是由于初始參數的影響,常常導致有用的特征信號被篩選清除。使用小波分解處理方法,因小波基參數需要多次實驗分析確定,缺少信號處理的泛化性。EMD可以對信號進行自適應分解,但是會產生嚴重的端點效應并具有模態混疊的缺點。
為了解決上述問題,本文采用一種集合經驗模態分解(Ensemble Empirical Mode Decomposition,EEMD)、主成分分析算法(Principal Component Analysis,PCA)和一維卷積神經網絡(one-Dimensional Convolutional Neural Network,1D-CNN)相結合的軸承故障識別的方法:首先將原始數據進行重構分解得到若干個本征模函數(Intrinsic Mode Function,IMF)分量,通過篩選能夠充分表達出數據特征的一條IMF分量再進行PCA算法去冗余處理,其次將原始數據也經過PCA去冗余處理,并采用將PCA-IMF分量和經過處理的新數據作為一維卷積神經網絡(1D-CNN)的輸入數據,最后把處理后的數據投入到網絡中進行多次迭代訓練特征提取分類,為滾動軸承故障預防和故障研究提供了一種新方法。
1 信號分析常用方法
1.1 EEMD算法
EEMD方法是為了彌補EMD模態混疊現象而提出的,通過對EMD分解后的若干個IMF分量添加對應的高斯白噪聲來改變分解過程中極值點的位置,從而可以有效地抑制模態混疊的產生。具體步驟如下:
(1)設定EEMD的運算次數z和高斯白噪聲標準差n。
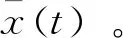
(4)重復步驟(1)和步驟(2)的操作z次后,篩選適當的IMF分量進行信號重構。
1.2 主成分分析(PCA)
當振動信號經過EEMD分解后仍存在干擾和冗余,這些干擾在網絡訓練時會影響網絡準確性,因此需要篩選并去除其中的干擾值,提高IMF分量的表現力。
PCA算法通過計算樣本向量中的特征值和均值,并通過投影運算便可以達到降維的目的。主要步驟如下:
(1)首先將數據進行中心化。
(2)計算樣本的協方差矩陣ZZi。
(3)對協方差矩陣ZZi進行特征值分解。
(4)取最大的d個特征值所對應的特征向量ωi。
(5)將ωi投影成矩陣。
1.3 卷積神經網絡(CNN)
隨著機器學習的發展,卷積神經網絡在數據處理及分類等方面取得了巨大的進步。卷積神經網絡是通過類似神經元的反應及反饋,利用卷積運算提取訓練樣本中的特征,其主要包括卷積層、池化層和全連接層。由于CNN超強的學習和特征提取能力因此廣泛用于工學的各個領域。
卷積層是通過卷積塊對數據進行局部運算并產生特征圖。池化層可以通過特征降維,提高網絡活性。全連接層是將上層傳入的數據進行進一步特征提取并將提取出的特征輸入Softmax函數進行分類。
2 故障診斷步驟
為了防止EEMD分解所帶來的特征缺失,提高模型的魯棒性和泛化性,提出基于EEMD分解和原始數據相互結合的方法。具體滾動軸承故障識別實驗方法如圖1所示。
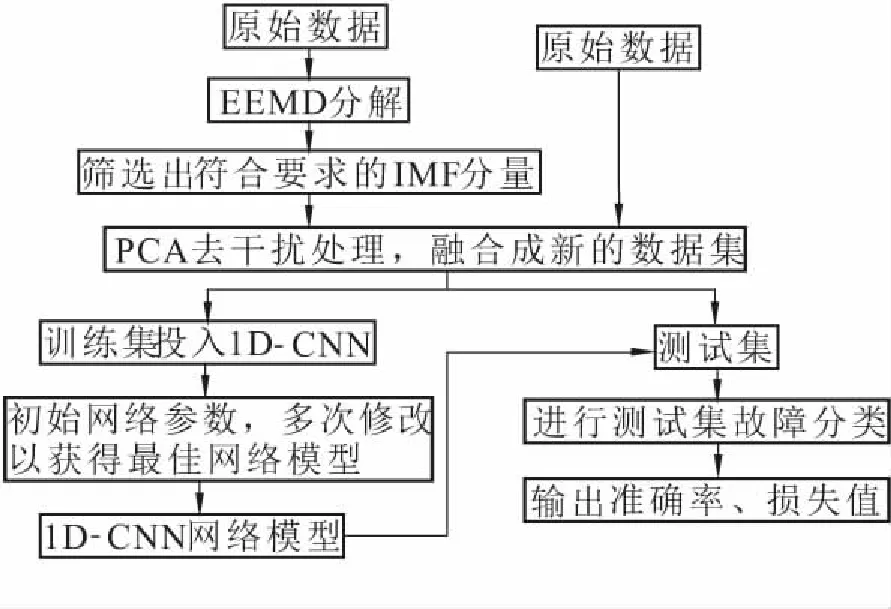
圖1 EEMD-PCA-1D-CNN故障分類流程
3 實驗驗證
3.1 信號處理
本文數據是采用美國西儲大學電機軸承故障狀況實驗,通過人為電火花破壞滾動軸承形成三種故障類型,對比正常類型,并篩選不同工況、載荷以及轉速下的振動信號,具體數據選取如表1所示。
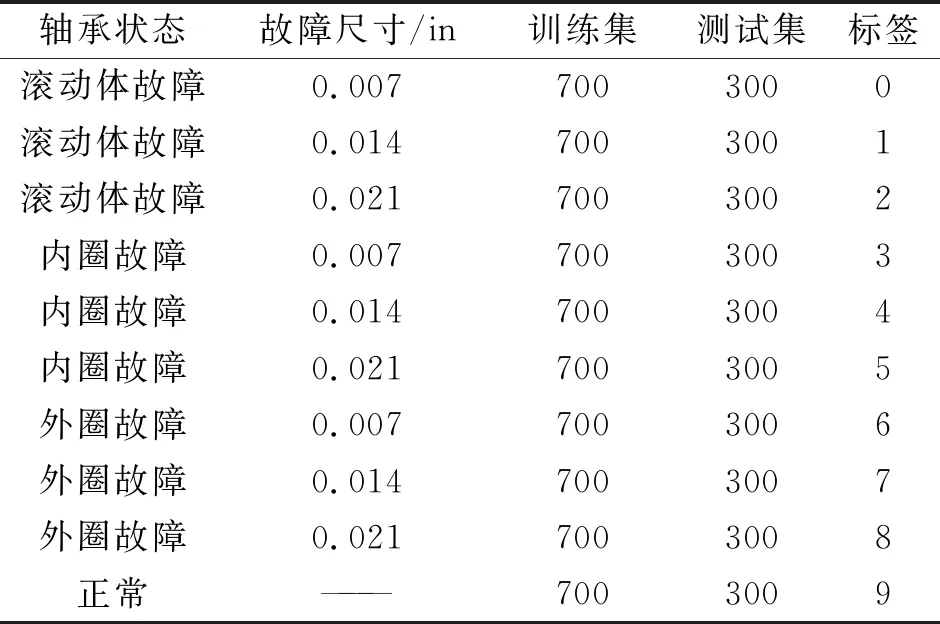
表1 軸承信號選取參數
根據本文上述的實驗方法,首先對數據進行EEMD處理,通過篩選適合的IMF分量對分解后的信號進行重構。相關系數可以用來表現分解后的IMF分量與原數據的相關程度。通過計算振動信號的譜峭度值ku可以發現運行系統中的異常,當軸承在正常運行時,譜峭度ku約等于3;當軸承發生故障或者運行不正常時,此時的譜峭度將會偏離正常值[5]。
相關系數的計算公式:
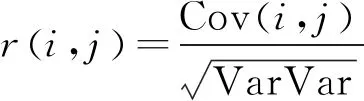
(1)
式中:i,j為兩個變量;Cov()為i,j的協方差;Var[]為i,j的方差。求得各IMF分量的相關系數并取絕對值,絕對值越大則表明該IMF分量所體現的故障振動信號所包含的原始信號相關程度越高。
根據上述的方法,計算各個IMF分量的相關系數和譜峭度,部分結果如表2、表3所示。為了體現EEMD算法更能體現出故障信號特征,因此將原始數據經過EMD分解設置為對照組,并計算對照組的相關系數和譜峭度值,部分結果同見表2、表3。
由表2、表3可知,軸承故障越嚴重,數據經過EEMD分解后所得譜峭度與正常值偏差更大,故障特征信息更明顯。由表2、表3可知,EEMD相比于EMD可以更有效的提取軸承信號的故障信息。通過計算分解后的各個IMF分量,將含有故障的軸承進行分解篩選,選取譜峭度與正常值3偏差較大、相關系數的絕對值較大的分量進行數據重構,并作為神經網絡的輸入數據集。

表2 EEMD-滾動體故障和EMD-滾動體故障(0.007 in)
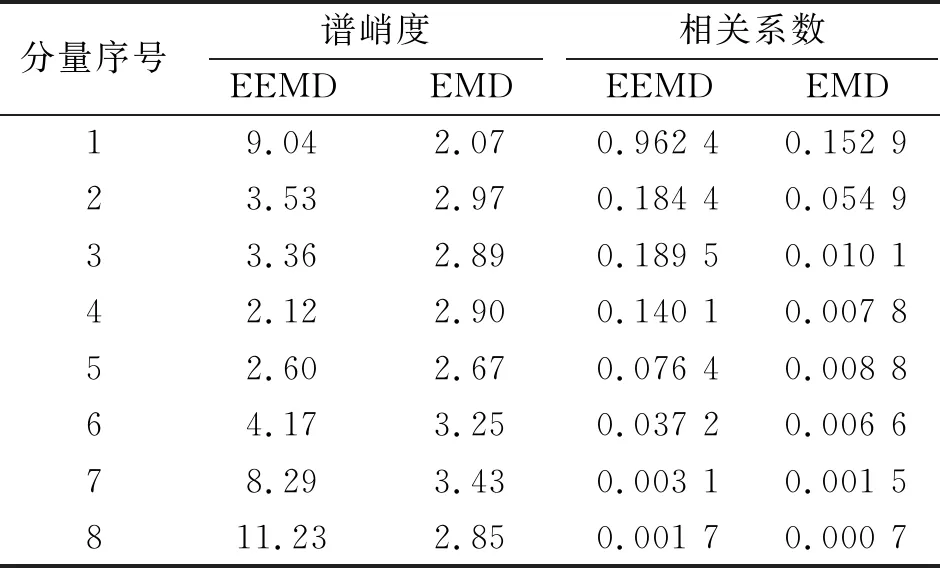
表3 EEMD-滾動體故障和EMD-滾動體故障(0.014 in)
3.2 網絡模型參數
將重構后的信號輸入主成分分析算法中計算,按照7∶3的比例分為測試集與訓練集,放入一維卷積神經網絡中。本文基于經典卷積網絡LeNet-5模型并多次調試,最終選取的各個參數如表4所示。

表4 卷積層參數
本次實驗所使用的深度學習框架為Tensorflow,編程語言為Python。計算機配置為銳龍R7-5800H,英偉達GeForce RTX3050Ti,16G內存。此次實驗每組數據中包括1 000個數據點,通過五折交叉驗證法確定最優網絡模型,測試階段重復5次,最終測試結果取均值。
4 實驗結果分析
通過多次對比實驗,10類故障信號分類準確率和損失值如圖2、圖3所示,經過500次迭代后準確率趨于穩定。通過t-SNE技術對原始數據和經過訓練的模型進行特征可視化分類,如圖4所示(只模擬分類擬合情況,橫、縱坐標無實際意義),未經過模型訓練的各個故障混亂,經過訓練后的模型故障標簽7和標簽8發生分類錯誤。通過圖5可知EEMD算法過程中存在端點效應而導致分類錯誤。
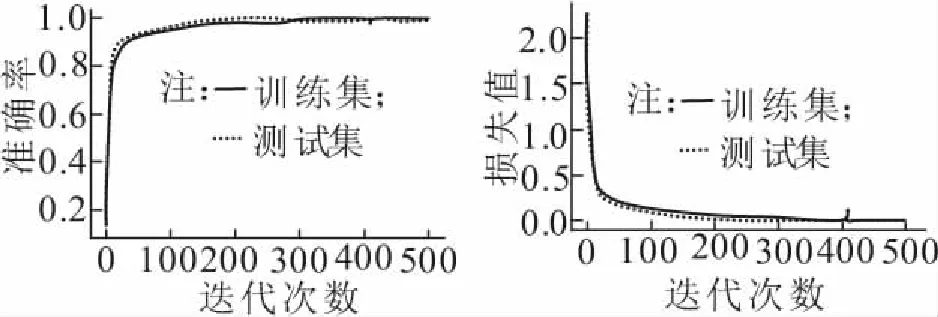
圖2 準確率 圖3 損失值

圖4 特征可視化 圖5 混淆矩陣
5 對比實驗驗證
為了驗證本文所采用的軸承診斷方法的適用性和準確性,通過使用機器學習中的分類方法對處理后的數據進行對比。將上述處理好的數據作為輸入數據輸入到EEMD-CNN和隨機森林中,10次實驗測試結果為:本文方法平均準確率98.6%,EEMD-CNN平均準確率92.3%,EEMD-隨機森林平均準確率86.6%。可知,通過使用EEMD-PCA-1DCNN的方法可以有效的提取故障類型的振動信號特征并分類,相比于其他算法有最高的平均準確率(98.6%),特征識別及分類效率有著明顯的提高,證明本文所提方法的可行性與有效性。
6 結束語
因軸承故障的振動信號復雜且包含有多種干擾,本文提出一種基于EEMD-PCA-1D-CNN的故障診斷方法,由對比結果可知,本文的方法在軸承故障診斷分類中準確率更高。本文在EEMD處理時數據產生了端點效應而導致準確率降低,還應探究多種網絡及算法優化以獲得最優模型,并通過變工況設計實驗增加網絡模型的魯棒性和泛化性。

