部分定體積幾何體的表面積極值討論部分定體積幾何體的表面積極值討論

◎王麗萍 張萬龍

(首鋼工學院基礎學院，北京 100144)

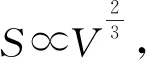
本討論中用到了極值思想.極值問題是經典微積分學中最成功的應用，無論在科學研究，還是在實際工程中、運籌規劃方面，將問題轉化為求解某種極值是十分常見的.

一、定體積圓臺表面積極值

再將上述表達式代入表面積公式S中，得到表面積表達式為

(1)

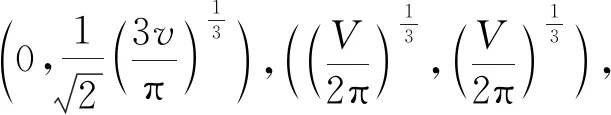
(2)

又因為圓錐的表面積為

S=πR2+πRl.

(3)

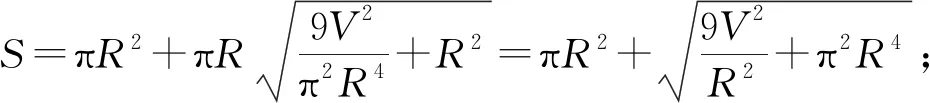
(4)

將(4)式兩邊平方，然后化簡得:

2Sx2-S2x+9V2π=0,

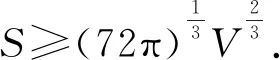
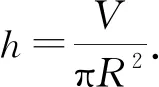
S=2πR2+2πRh

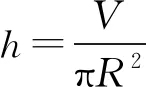
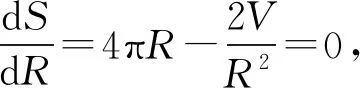
二、定體積球缺表面積極值

S=π(2Rh+R2-(R-h)2)=π(4Rh-h2).

(5)

(6)

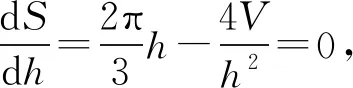
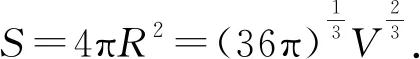
三、定體積長方體表面積極值

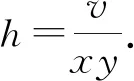
(7)

下面通過兩種方法求其表面積公式(7)的極值.

(一)初等方法

即

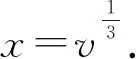
因此，當長方體的表面積取得最小值時，正是同體積下正方體的表面積.

(二)極值法

分別對(7)式中的x,y求偏導得下面的偏導公式：

(8)

(9)

令(8)(9)兩式為0，得到以下偏導方程組：

(10)

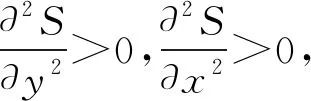
四、定體積錐球結合體的最小表面積

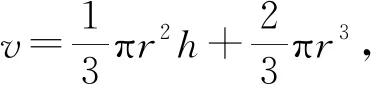
(11)

通過計算組合體的表面積，得到表面積公式為：

s=πrl+2πr2.

(12)

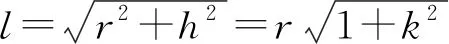
將斜高公式代入組合體的表面積公式，得

(13)

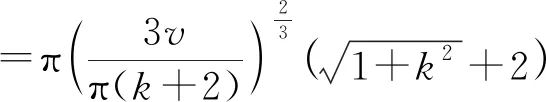
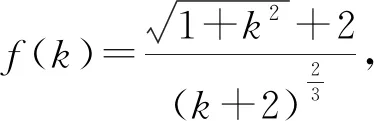
對f(k)求導可得到

化簡可得到

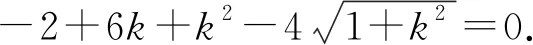
五、結束語

通過對定體積圓臺、球缺、長方體表面積極值的討論，我們可以發現：定體積圓臺取得最大表面積時為圓錐，取得最小表面積時為圓柱；定體積球缺取得最小表面積時為球體；定體積長方體取得最小表面積時為正方體.本文通過比較幾何體表面積的極值，發現了36π<54π<216<72π，因此對于體積一定的幾何體，最小表面積從小到大的排列順序為球體、圓柱體、正方體、圓錐體，同時，也能得到體積相等的立體圖形，越接近球，表面積越小的結論.