Bernoulli泛函空間上的算子構造的量子隨機游蕩模型Bernoulli泛函空間上的算子構造的量子隨機游蕩模型
◎張 銀 李 唯
(吉利學院智能科技學院,四川 成都 641402)
一、引言
量子概率理論 (von Neumann) 以二元組(A,φ)為概率空間,其中A是一個von Neumann 代數,φ是A上的態 (即定義在A上的非負正規線性映射).A中的投影算子稱為量子隨機事件,因投影算子的乘積未必是投影算子,從而量子隨機事件一般不構成σ-代數,但如果它們的乘積可交換,則構成σ-代數,于是化為經典情形.在這個意義上稱量子概率論為非交換的概率論,經典概率論屬于它的特殊情形.作為經典概率論的非交換推廣,量子概率論中的一些概念可看作經典概率論中相應概念的直接推廣,如,量子隨機變量、量子隨機過程、量子Markov 鏈、量子Markov過程等.作為另一類重要的隨機過程,經典隨機游蕩在傳統的信息技術處理領域有著非常廣泛的應用.
隨著量子信息理論在20世紀90年代的研究熱潮,量子隨機游蕩(quantum random walk)成為一種新的游蕩模式,這種新的模式開始被人們所關注,它在量子信息理論和量子計算等領域中有著廣泛的應用.量子隨機游蕩簡稱為量子游蕩,是基于量子力學原理的一種隨機游蕩,我們可將其看作經典隨機游蕩的量子類似物,由于量子隨機游蕩的演化速度遠遠快于經典的隨機游蕩,因此,它們的演化行為與經典的隨機游蕩有著極大的不同.
2008年,Privault給出了關于Bernoulli噪聲泛函的兩種運算——散度運算和梯度運算,并在這基礎上,構建了一種Malliavin型隨機分析框架.2010年,Nourdin等研究了一種對稱型的Bernoulli泛函的正態逼近,這種對稱型的Bernoulli泛函也叫作Rademache泛函.2011年,王才士等在根據Privault的Malliavin型隨機分析框架,定義了增生和湮滅兩種算子,證明了這兩種算子滿足等時典則反交換關系,并利用這兩種算子給出了量子Bernoulli噪聲的定義.2015年,針對一類具有有限多個內部自由度的開放型量子隨機游蕩,Attal運用經典Markov鏈方法證明了相應的中心極限定理.2016年,量子Bernoulli噪聲首次被王才士等用在了量子隨機游蕩的研究當中,并利用量子Bernoulli噪聲構建了一種量子隨機游蕩模型,這種模型是定義在一維整數格上的具有無窮多個內部自由度的離散時間量子隨機游蕩模型,可歸于酉量子隨機游蕩的范疇.從文獻[1]的結論可看出,該模型在特殊的初始態下,與經典隨機游蕩模型有相同的極限概率分布.因此,該量子隨機游蕩呈現了強烈的退相干效應.
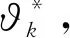
本文組織結構如下.第一部分,主要回顧一些基本概念和事實.第二部分,給出了定義在Bernoulli泛函空間上的兩類新算子,并研究了這兩類算子的性質,利用這兩類算子構造了一種量子隨機游蕩模型,給出了該模型在任意初始態下的態及其概率分布,證明了該量子隨機游蕩在某些特殊的初始態下的極限分布為正態分布,此結果與經典隨機游蕩模型的極限概率分布相同.
二、預備知識
本章先簡單介紹Bernoulli泛函空間相關的概念、記號以及結論,詳細內容可見文獻[1].
Γ={σ|σ?,#σ<∞},這里#σ表示σ中元素的個數.設n≥0是非負整數,則記Γn={0,1,…,n}.此處,當σ=?時,約定maxσ=-1,否則maxσ表示σ中的最大數.
設Ω={-1,1}表示所有映射ω:{-1,1}構成的集合.以(ζn)n≥0表示定義在Ω上的典則投影序列,即對每個n≥0,投影ζn由ζn(ω)=ω(n),ω∈Ω來定義.
令I=σ(ζn;n≥0),即I表示Ω上由序列(ζn)n≥0生成的σ-域.設(pn)n≥0是給定的正數序列,這里0 其中k,nj∈,εj∈{-1,1}(1≤j≤k),當i≠j時,ni≠nj,因此,就能得到一個概率測度空間(Ω,I,P),此概率測度空間(Ω,I,P)稱為Bernoulli空間. 利用序列(ζn)n≥0可定義(Ω,I,P)上的隨機變量序列: 因此,Z=(Zn)n≥0可看作離散時間的Bernoulli噪聲.并且,我們還可以證明I=σ(Zn;n≥0)是由Bernoulli噪聲(Zn)n≥0生成的σ-域.因此,我們把Bernoulli空間(Ω,I,P)上的隨機變量也叫作Bernoulli噪聲的泛函,簡稱Bernoulli泛函.為了簡便,用In=σ(Zk;0≤k≤n)表示Ω上由(Zk)0≤k≤n生成的σ-域,其中n≥0,且I-1={?,Ω}. 本節首先定義了兩類Bernoulli空間上的單位算子,并討論了這兩類算子的性質.其次,利用這兩類算子構造了一種量子隨機游蕩模型,考察了所給出的量子隨機游蕩模型的動力學性質,證明了該量子隨機游蕩在任意初始態下的態以及概率分布,該結果表明,本文所構建的模型具有強局部化性質.最后,證明了其在真空初始態下的極限分布為正態分布. 定義2.1對任意k≥0,在H上存在一個有界算子?k,使得 ?kZσ=Zσk,σ∈Γ, 其中σk=σ{k},且‖?k‖=1,稱?k為差算子. 證明?σ∈Γ有 ?k?lZσ=?k(?lZσ)=?kZσl=Zσ{k,l}, ?l?kZσ=?l(?kZσ)=?lZσk=Zσ{k,l}, 同理可證,?k?k=?k. 定義2.4設l2(Ζ,H)表示整數格上的離散時間量子隨機游蕩模型的態空間,其態由l2(Ζ,H)中的標準正交基線性表示,其時間演化滿足方程 其中Φn表示該量子隨機游蕩在n時刻態,n≥0,特別地,Φ0表示初始態. 引理2.5設量子隨機游蕩的初始態Φ0∈l2(Ζ,H)滿足:Φ0(x)∈Hn-1,x∈,其態序列(Φn)n≥0具有如下性質: {Φn(x)|x∈}?Hn-1,n≥1, Hn-1是前一段所定義的子空間. 上述引理說明,當量子隨機游蕩的初始態滿足適當的條件時,其態序列滿足某種“可料”性質.結合文章所給量子隨機游蕩模型和上述引理,我們利用數學歸納法,能夠給出量子隨機游蕩在任意初始態下,各個時間態的具體形式. 定理2.6設量子隨機游蕩模型的初始態Φ0∈l2(Ζ,H)為: 這里f(σ)∈,且則對于n≥1就有 證明根據引理2.5,Φ0(x)∈Hn-1,x∈. 易見,當x∈{-1,1}時,Φ1(x)=0, 因此,定理對于n=1成立; 假設n=k,k≥1時,定理成立; 那么,當n=k+1時,x?{2j-(k+1)|0≤j≤k+1}時,Φn+1(x)=0,那么 Φk+1[2j-(k+1)] 則當n=k+1時,定理成立; 綜上,定理成立,證畢. 定義2.4中,通過函數x‖Φn(x)‖2,我們給出了定義在整數格上的一個概率分布,把它稱為量子隨機游蕩在n≥0時刻,x∈位置的概率分布,這里,‖Φn(x)‖2表示在n≥0時刻,x∈處發現量子游蕩者的概率.利用定理2.6的結論,我們就能給出了量子隨機游蕩在真空初始態下, 量子隨機游蕩的概率分布. 定理2.7設新模型的初始態Φ0∈l2(Ζ,H)如定理2.6中所示,則對于n≥1,就有 P{Xn=x}=‖Φn(x)‖2 證明這里我們直接利用定理2.6的結論.由于 并且當x?{2j-n|0≤j≤n|}時,P{Xn=x}=‖Φn(x)‖2=0,證明完畢. 下面一個定理給出了量子隨機游蕩在真空初始態的條件下,量子隨機游蕩的態,該定理說明本文中的量子隨機游蕩模型具有很強的局部化性質. 則對一切n≥1,有 證明這里直接利用定理2.6的結論.取σ=?,f(σ)=1,就有 得證. 定理2.9設量子隨機游蕩模型的初始態為真空初始態,當對于n≥1,量子隨機游蕩模型就有如下的概率分布 證明這里我們直接利用定理2.6的結論,由于 那么,當x=2j-n,0≤j≤n,時, 并且當x?{2j-n|0≤j≤n}時,就有:P{Xn=x}=‖Φn(x)‖2=0,證明完畢. 下面一個定理給出了量子隨機游蕩模型在真空初始態下的極限分布. 上述定理說明,本文所給出的模型在真空初始態下的極限分布是標準正態分布,這與經典的隨機游蕩有著相同的極限分布. 本文定義了在Bernoulli泛函空間上的兩類新算子,利用這兩類算子構造了一種量子隨機游蕩模型,給出了量子隨機游蕩模型在任意初始態下的態以及概率分布,又給出了該模型在真空初始態下的態、概率分布以及其極限分布.在未來,我們可以考慮該模型在開放的量子系統中的表示,并且可以討論該模型在一般初始態下的極限分布.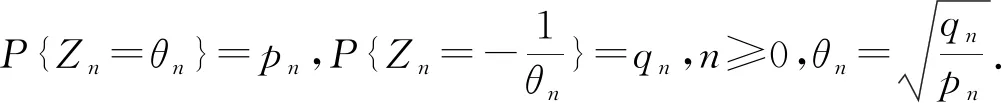
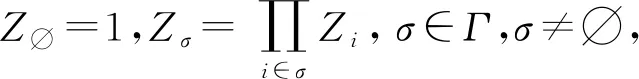
三、主要結果及證明
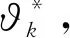
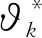
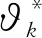
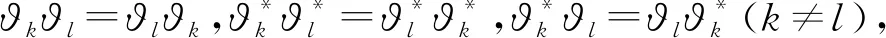
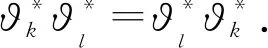
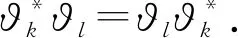
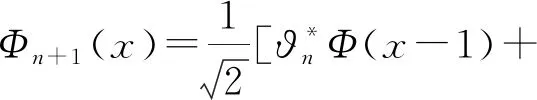

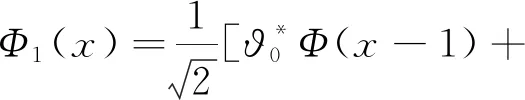
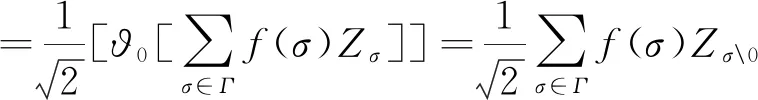
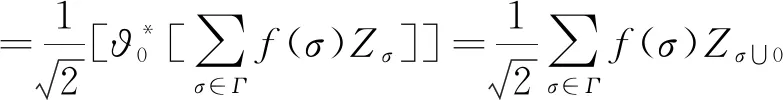
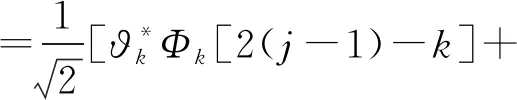
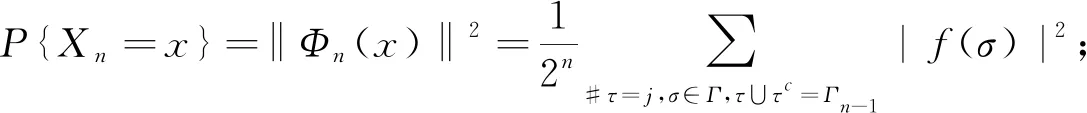
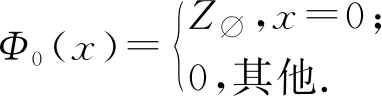
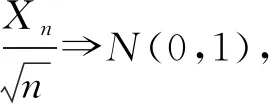
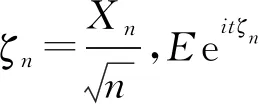
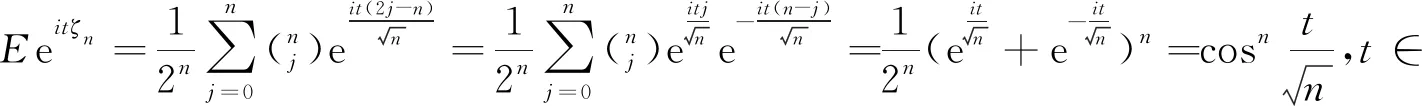
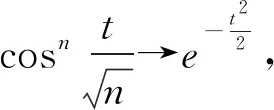
四、總結與展望

