爆炸地震動下儲液結構動力響應試驗研究

張浩天， 趙雪川， 宋春明， 吳紅曉， 鄭際鏡， 岳松林， 程怡豪

(1. 陸軍工程大學 爆炸沖擊防災減災國家重點實驗室， 南京 210007； 2. 96911部隊， 北京 100010)

世界格局與戰爭形態不斷演變，各國爭相運用高新技術研發和改進武器裝備。在持續緊張的安全形勢之下，國防工程建設與防護技術研究面臨著嚴峻的挑戰。作為工程防護關注的特種結構之一，儲液結構(liquid storage structures ，LSS)在給排水系統和石油化工等方面有著重要的應用，關乎水源、油料等戰略資源的儲備安全[1-3]。在面臨突發武器打擊和偶然爆炸襲擊，特別是核武器爆炸時，強烈的沖擊地震動將導致儲液結構產生動力響應，嚴重時將造成結構的損傷破壞，乃至引發巨大的次生災害，對人民群眾的生命和財產安全造成極大的威脅[4-6]。因此，有必要開展爆炸地震動下儲液結構的動力響應研究，對于補充和完善國防工程理論體系，提高工程防護能力具有重要意義。

當前，國內外學者圍繞儲液結構開展了大量研究工作。其中，儲液結構動力特性研究是分析結構動力響應的基礎，魏發遠等[7-9]將儲液容器簡化為梁式結構，分別基于懸臂梁彎曲、剪切、彎剪變形理論建立了儲液結構的振動方程，并指出工程應用時可根據結構高寬比選用不同變形理論進行近似計算。Kim等[10]對儲液結構單一壁板進行分析，建立了固支-自由-對邊簡支板和固支-自由-對邊固支板兩種計算模型，發現隨著壁板長高比的增大，結構基頻逐漸趨近于懸臂梁模型計算結果。Hashemi等[11]提出了儲液結構四面壁板的振動分析方法，在水平和豎直方向分別利用連續梁和懸臂梁變形理論，組合得到了儲液結構折板振型。楊鳴等[12]基于聲固耦合算法分析儲液容器固有特性，發現液體的附加質量效應使得結構的固有頻率下降，增大了結構在低頻荷載下發生強烈振動的可能性。杜永峰等通過數值算例得到類似的結論，指出液動壓力使結構自振頻率明顯下降，同時發現在儲液條件下結構振型變化不大，在分析其振動響應時可使用無液結構振型近似替代。程選生等[13]針對Winkler彈性地基和彈性構造底板的情況，推導了儲液結構液-固耦合振動方程，討論了無量綱參數對自振頻率的影響。

關于儲液結構動力響應，現有研究多以自然地震動作為輸入載荷，進行理論推導、數值分析與振動臺模型試驗。地震激勵下需要考慮液體與結構的相互作用問題，以達到科學安全的設計要求。Housner[14]提出了剛性儲液結構計算簡化模型，將液動壓力分為兩部分：一是隨結構作同步運動的液體產生的脈沖壓力；二是結構內液體晃動產生的對流壓力，并將液體等效為與結構相連的彈簧-質量系統，在儲液結構設計中被廣泛應用。Veletsos[15]將儲液結構考慮為單自由度體系，并假定結構按照給定形式發生撓曲變形，提出了彈性儲液結構簡化計算方法，發現考慮結構柔性時液動壓力有所增加。Chen等[16]基于廣義單自由度理論并考慮懸臂梁變形邊界條件進行儲液結構動力響應案例分析，發現單自由度方法用于儲液結構設計具有較高的精度，同時應考慮高階模態的影響。Kim等、Hashemi等提出了考慮流固耦合作用和壁板彈性的柔性儲液結構動力響應計算模型，在計算脈沖壓力時疊加了壁板變形引起的脈沖壓力。特別地，針對帶有彈性壁板的鋼筋混凝土儲液結構，程選生等[17]推導了液動壓力計算公式。程選生等[18]采用ADINA軟件建立儲液結構有限元模型，考慮了液體表面重力波的影響，探討了地震烈度和液位高度對液晃波高和結構壁板變形的影響。張如林等[19]建立流固耦合運動方程并利用ANSYS軟件建模，分析了地震波頻譜特性對儲液結構地震響應的影響，發現當地震波卓越周期接近流固耦聯振動周期時，結構響應顯著增強。Radnic等[20]利用振動臺進行地震激勵下儲液結構的動力響應試驗研究，討論了激勵特性、壁板剛度與儲液水位等參數對結構動力響應的影響。程選生等[21-22]采用人工黏彈性邊界模擬地基效應進行有限元分析，發現考慮土-結構相互作用后，內部水體液動壓力和儲液結構動力響應均有較大程度的減小。

綜上所述，儲液結構在生命線工程中具有重要應用，其安全性備受關注，地震激勵下儲液結構的動力響應研究已經取得了一些成果。然而，以往研究側重于自然地震動下儲液結構響應，在方法上則偏重于理論計算和模擬仿真。相比之下，爆炸地震動加速度信號具有峰值大、持時短等特點，該震動環境下儲液結構動力響應研究較少，特別是在試驗方面，由于操作難度大、危險系數高、成本高等，成功案例鮮有，缺少能夠指導工程實踐的規律性發現，也不足以有效驗證和補充相關理論與數值研究結果。因此，本文開展爆炸地震動下儲液結構動力響應試驗研究，對不同強度地震動下，處于無水、淺水、深水液位狀態的儲液結構進行振動臺試驗，同時結合理論方法與相關設計規范，分析結構振動加速度、結構變形、動水壓力等動力響應的變化規律，以期為國防工程中儲液結構的研究與設計提供有益參考。

1 試驗概況

1.1 試驗設備

結構試驗于爆炸沖擊震動模擬平臺進行，如圖1所示。該平臺由陸軍工程大學爆炸沖擊防災減災國家重點實驗室研制，用以模擬核武器爆炸沖擊震動環境[23]。平臺試驗時，用掛鉤吊住擺錘，卷揚機通電提升擺錘至預定高度后釋放，自由下落的擺錘撞擊振動臺，提供單次近半正弦加速度脈沖，通過調整擺錘下落高度與緩沖墊塊厚度，可改變輸入加速度波的峰值與脈寬。其中，下落高度定義為擺錘自釋放至水平撞擊振動臺，其錘頭重心下降高度，示意圖如圖2所示。需要說明的是，爆炸震動與爆炸參數、介質條件、結構特性等因素有關，該平臺以沖擊荷載對爆炸震動環境進行模擬，究其原理：一是反應譜等效[24-25]，將結構系統簡化為若干單自由度系統，爆炸震動對結構的作用效果與對各單自由度系統作用效果相同時，可對爆炸震動加速度信號進行反應譜分析，并以半正弦加速度信號反應譜包絡，則半正弦加速度脈沖峰值和脈沖持時即為相應爆炸震動加速度等效值；二是波形等效，爆炸地震動的波形難以準確預測，通常采用某一較符合實際情況的假定波形進行參數分析。設計中可近似將自由場地運動參數取為結構運動參數，而半正弦類脈沖及其主導的加速度信號是爆炸試驗典型波形之一[26-27]。

圖1 爆炸沖擊震動模擬平臺Fig.1 Explosion shock and vibration simulation platform

圖2 擺錘自由下落Fig.2 Free falling of the pendulum bob

1.2 模型結構及傳感器布置

試驗模型為地面式矩形無頂蓋儲液結構，其尺寸特征參考地下工程典型儲液結構，如圖3所示。模型材料為201不銹鋼，長1 200 mm，寬900 mm，高750 mm，壁厚10 mm，存儲液體為常溫常壓下的自然常用水。儲液結構底板與震動平臺對應布置φ30 mm孔洞，通過螺栓連接，結構長邊平行于加載方向。動力試驗過程中，布置一系列傳感器來記錄各種參數，如圖4所示。其中，加速度傳感器(記為A)與動水壓力傳感器(記為P)沿加載方向布置，分別測量加載后結構的振動響應、結構受到的動水壓力，應變片(記為S)沿結構短邊方向布置，反映結構的變形情況，以上傳感器均為單向式。

圖3 矩形儲液結構Fig.3 Rectangular LSS

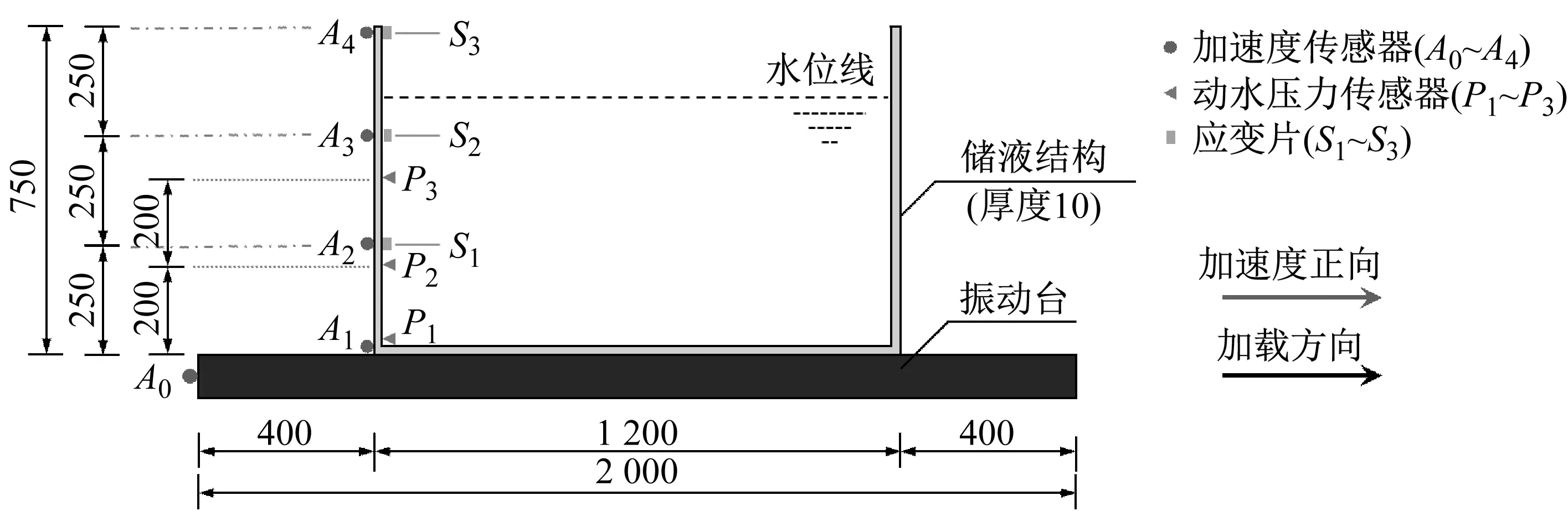
圖4 傳感器布置 (mm)Fig.4 Sensors layout (mm)

1.3 試驗工況

分別進行爆炸地震動下無水、300 mm儲水、500 mm儲水結構動力響應試驗，墊塊厚度50 mm，通過調整擺錘下落高度H1～H5，提供5種幅值的輸入加速度。其中，H1～H5分別為1 140 mm，1 340 mm，1 540 mm，1 740 mm， 1 940 mm。500 mm儲水、擺錘高度H3時得到的典型輸入加速度時程曲線，如圖5所示。該工況下獲得幅值15.8g、持續時間15.5 ms的單次加速度脈沖。可以看出，結構底部A1處與振動臺臺面A0處采集的加速度時程曲線一致性較好，說明螺栓連接緊實可靠，保證了加載過程中振動臺與結構之間無相對滑移，試驗的有效性得到驗證。

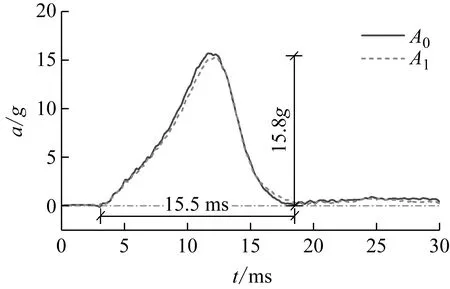
圖5 典型輸入加速度時程曲線Fig.5 Typical time history curve of input acceleration

對于每種工況進行至少兩次平行試驗，在試驗結果差值小于兩者平均值5%的前提下取平均值作為可信數據進行后續分析，否則補充第三次及以上試驗直至滿足可信條件。不同工況下得到的地震動參數如表1所示，地面峰值加速度(peak ground acceleration,PGA)范圍為10.0～26.4g，持續時間(duration time of ground acceleration, TGA)平均值為14.8 ms。經查閱文獻資料[28-29]，了解到加速度型地震動強度參數可以較好地表征地震動對結構的潛在破壞作用，同時考慮到GB 50011—2010《建筑抗震設計規范》[30]將峰值加速度作為地震動強度指標，本文亦選取峰值加速度這一參數描述地震動強度特性，以便于分析爆炸地震動對儲液結構動力響應的影響。此外，由于篇幅有限，而不同地震動輸入條件下動力響應時程曲線變化規律基本一致，僅展示500 mm儲水、15.8g地震動強度(擺錘高度H3)時得到的典型時程數據，并分析儲液狀態、地震動強度對響應峰值等參數的影響。

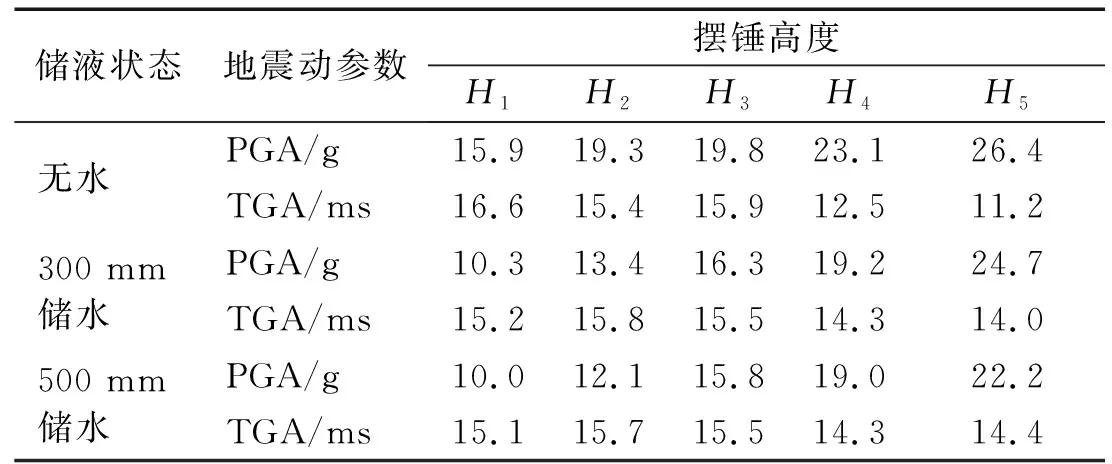
表1 不同工況下地震動參數Tab.1 Seismic load parameters under different working conditions

2 試驗結果與分析

2.1 結構動力特性分析

結構的動力特性包括固有頻率、阻尼比、振型等，通常認為固有頻率對擋墻等短周期結構的地震響應有很大影響[31]。本文振動臺模型試驗中，通過傳遞函數分析法確定結構的動力特性參數[32]，傳遞函數Ha(ω,zj)計算為

(1)

式中：GXX(ω)為振動臺臺面A0處加速度時程信號的自功率密度函數；GXY(ω,zj)為結構測點Aj(j=2,3,4)處加速度時程與振動臺臺面A0處加速度時程信號的互功率密度函數。描繪復函數Ha(ω,zj)的幅值-頻率曲線，其首個峰值對應的頻率fn即為結構固有頻率。

不同儲液狀態下得到的加速度傳遞函數幅值-頻率曲線，如圖6所示。由圖6可知，結構壁板不同高度測點A2，A3，A4得到的結構固有頻率基本一致，取3處測點計算結果的平均值為結構固有頻率。相比于無水結構(fn=54.15 Hz)，300 mm儲水結構(fn=48.84 Hz)和500 mm儲水結構(fn=38.56 Hz)自振頻率分別下降9.82%，28.80%，說明儲液深度的增加使儲液結構固有頻率下降，與以往杜永峰等和楊鳴等研究的結論一致。

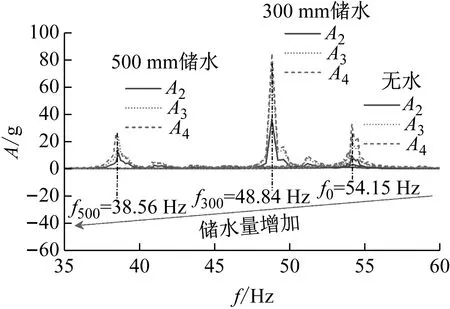
圖6 結構加速度傳遞函數幅值-頻率特性曲線Fig.6 Amplitude-frequency characteristic curve of structural acceleration transfer function

2.2 結構振動加速度響應分析

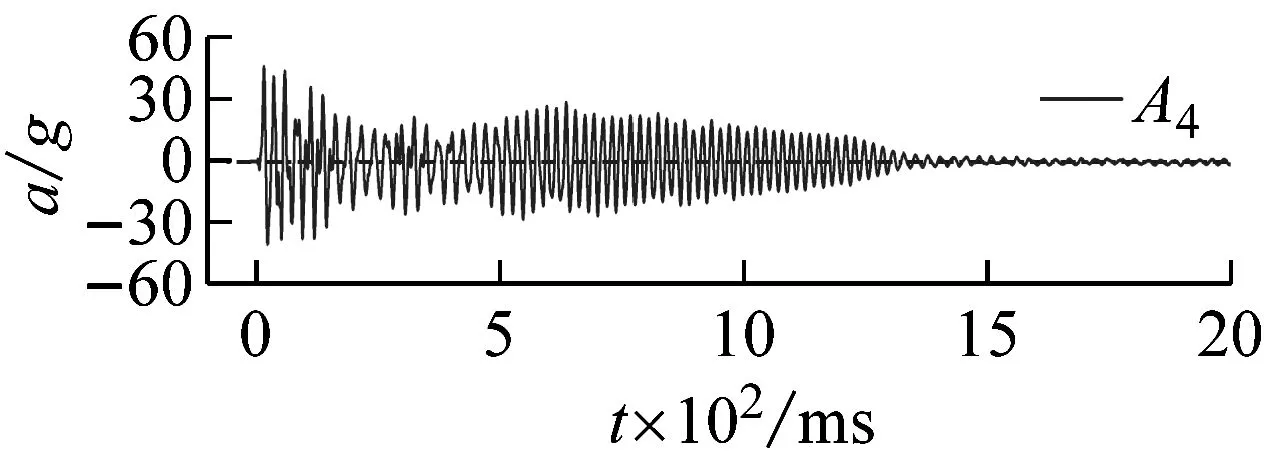
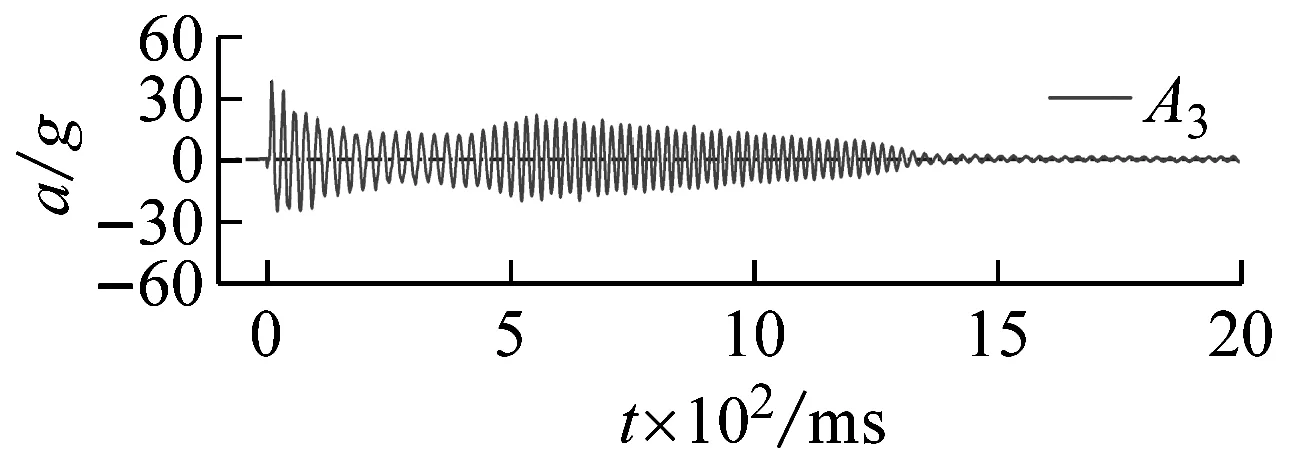
500 mm儲水、15.8g加載條件下，測點A2，A3，A4處結構振動加速度響應典型時程曲線，如圖7所示。由圖7可知，受沖擊荷載后結構振動加速度迅速達到峰值，在低阻尼作用下，往復振動幅值逐漸減小。加載后120 ms內輸入加速度與不同測點處結構加速度隨時間變化的規律，如圖8所示。由圖8可知，由振動臺臺面A0測點至頂部A4測點，加速度曲線峰值依次出現，說明地震動影響由底部逐漸傳至頂部。為了描述地震動從基礎傳遞到上部結構的變化情況，采用傳遞系數β表征結構加速度沿模型高度的放大或者衰減效應，β的定義為測點加速度峰值與臺面輸入加速度峰值的比值，即

(a)

(b)

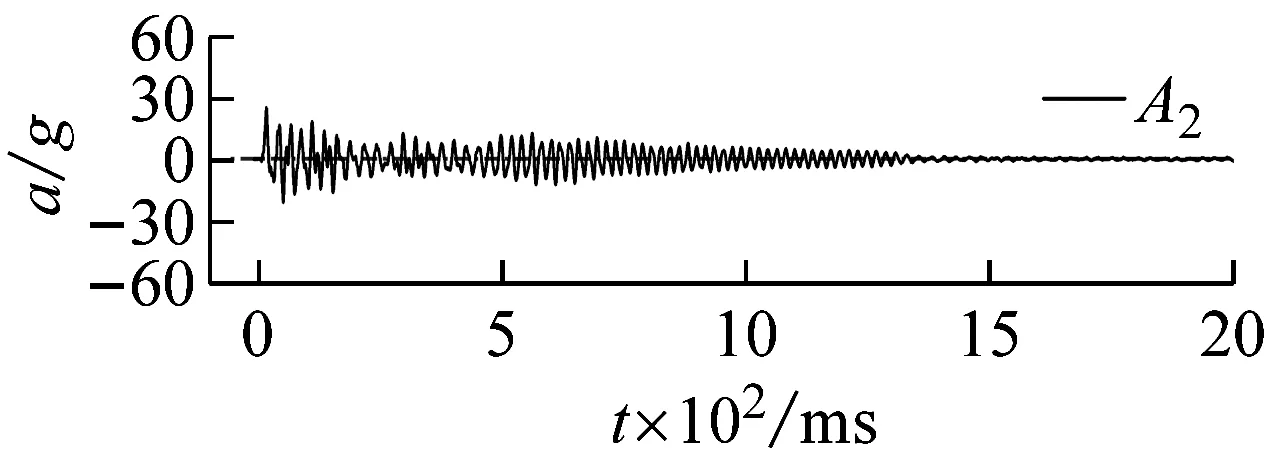
(c)圖7 結構加速度響應典型時程曲線Fig.7 Typical time history curve of structural acceleration response

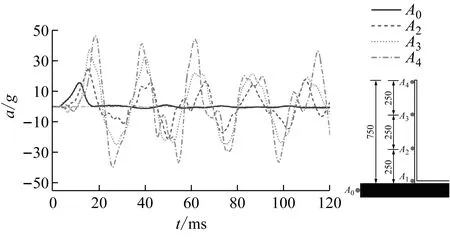
圖8 結構加速度響應規律對比Fig.8 The comparison of the law of structural acceleration response

β=ai/a0

(2)

式中：ai為壁板上A2～A4測點加速度峰值；a0為臺面A0輸入加速度峰值。

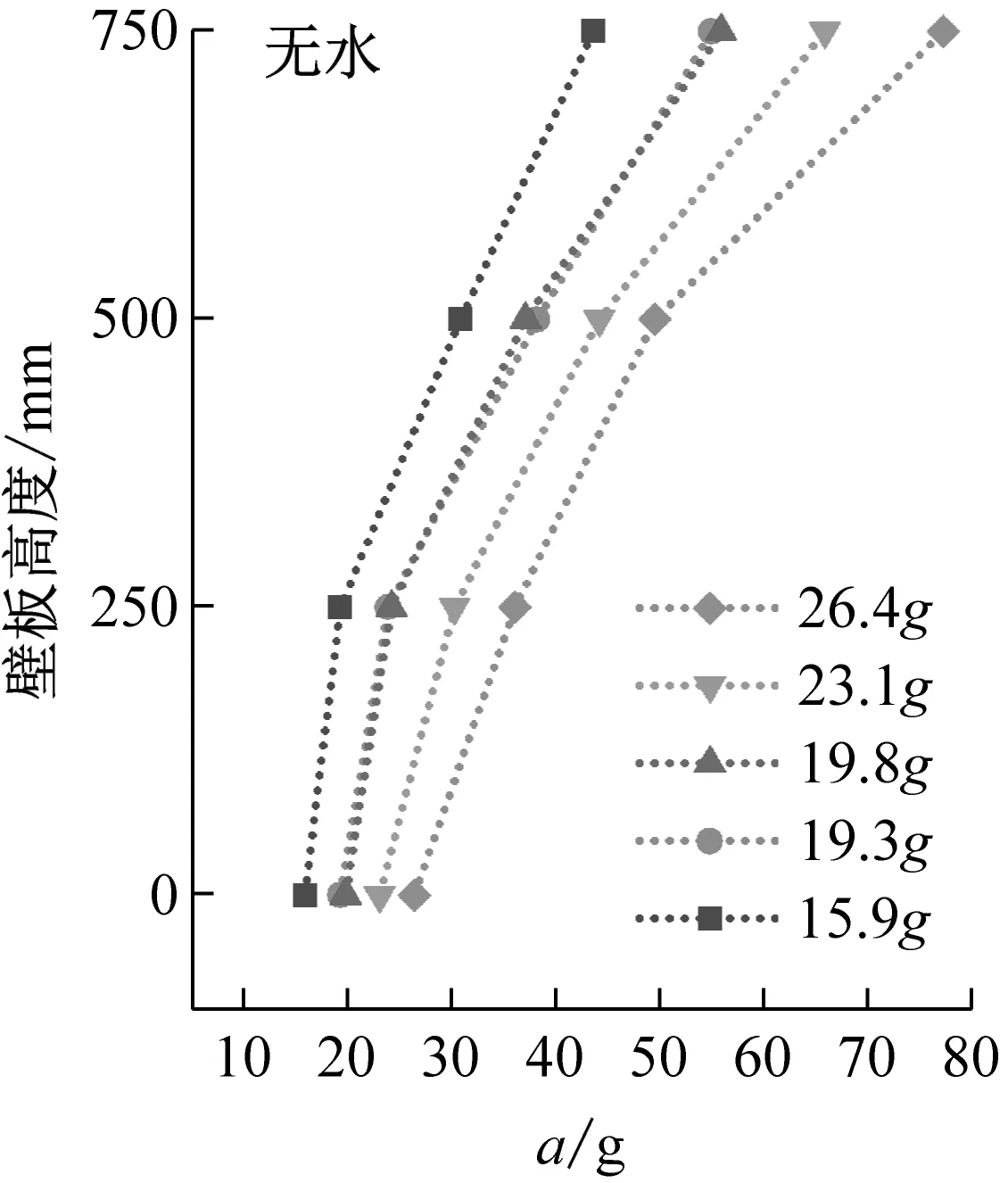
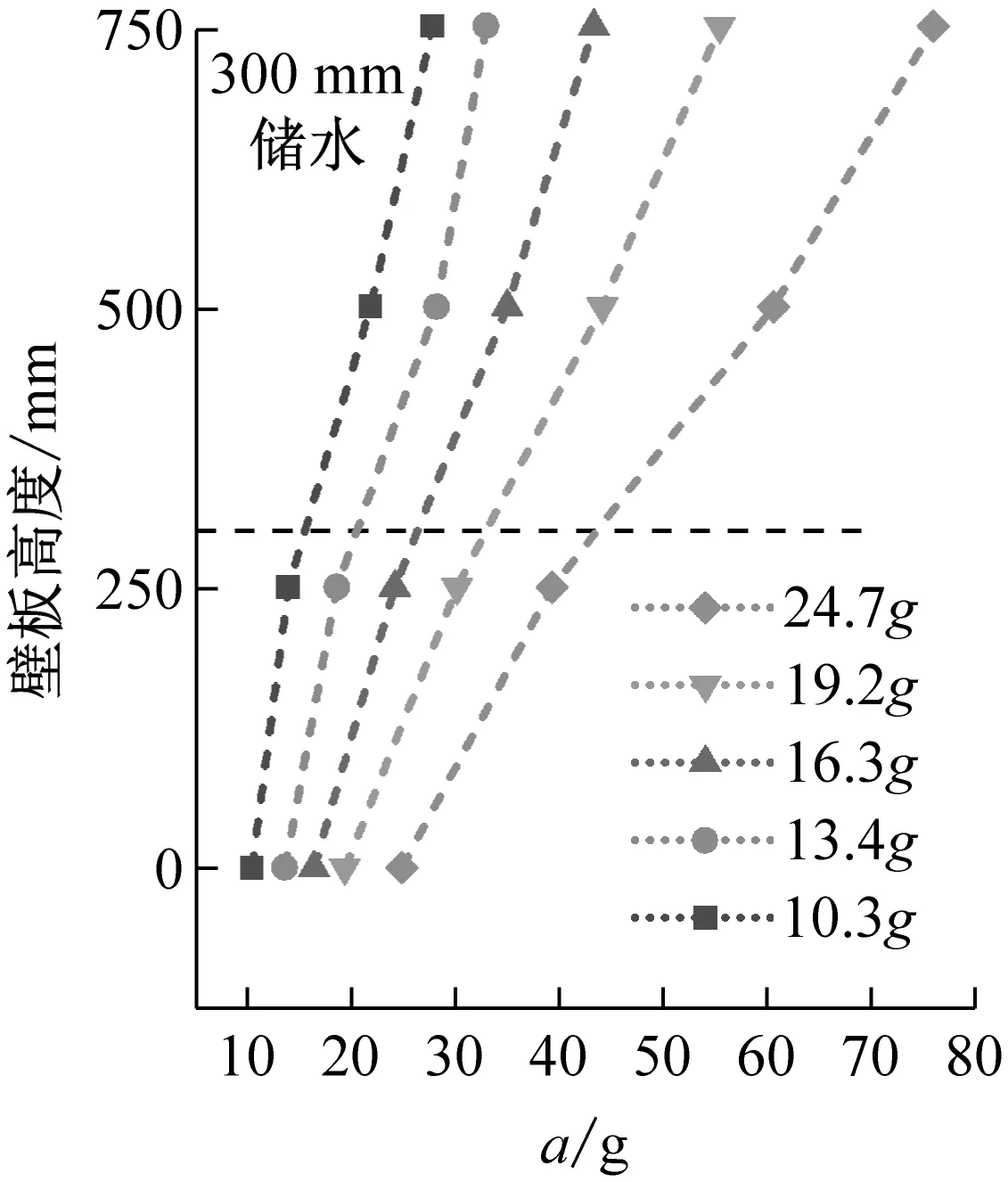
結構加速度峰值與加速度傳遞系數沿壁板高度變化規律，如圖9、圖10所示。由圖9、圖10可知，由壁板底部至頂部，加速度峰值呈現非線性增大趨勢，傳遞系數均大于1，說明地震動在由基礎向上部結構傳遞的過程中存在遞增的放大效應，在結構頂部放大效應最為明顯。無水條件下，結構加速度傳遞系數沿結構高度呈加速增大趨勢；儲水條件下，液面以下由于液體的附加質量效應，結構加速度放大效應更加顯著。因此，以儲水液面為劃分界面，加速度傳遞系數沿壁板底部至頂部呈現先加速增大、后減速增大的趨勢。

(a)

(b)

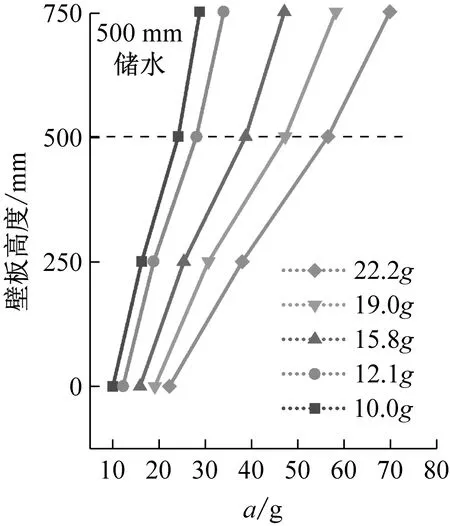
(c)圖9 加速度峰值沿壁板高度變化Fig.9 Peak acceleration varies along the height of the wall

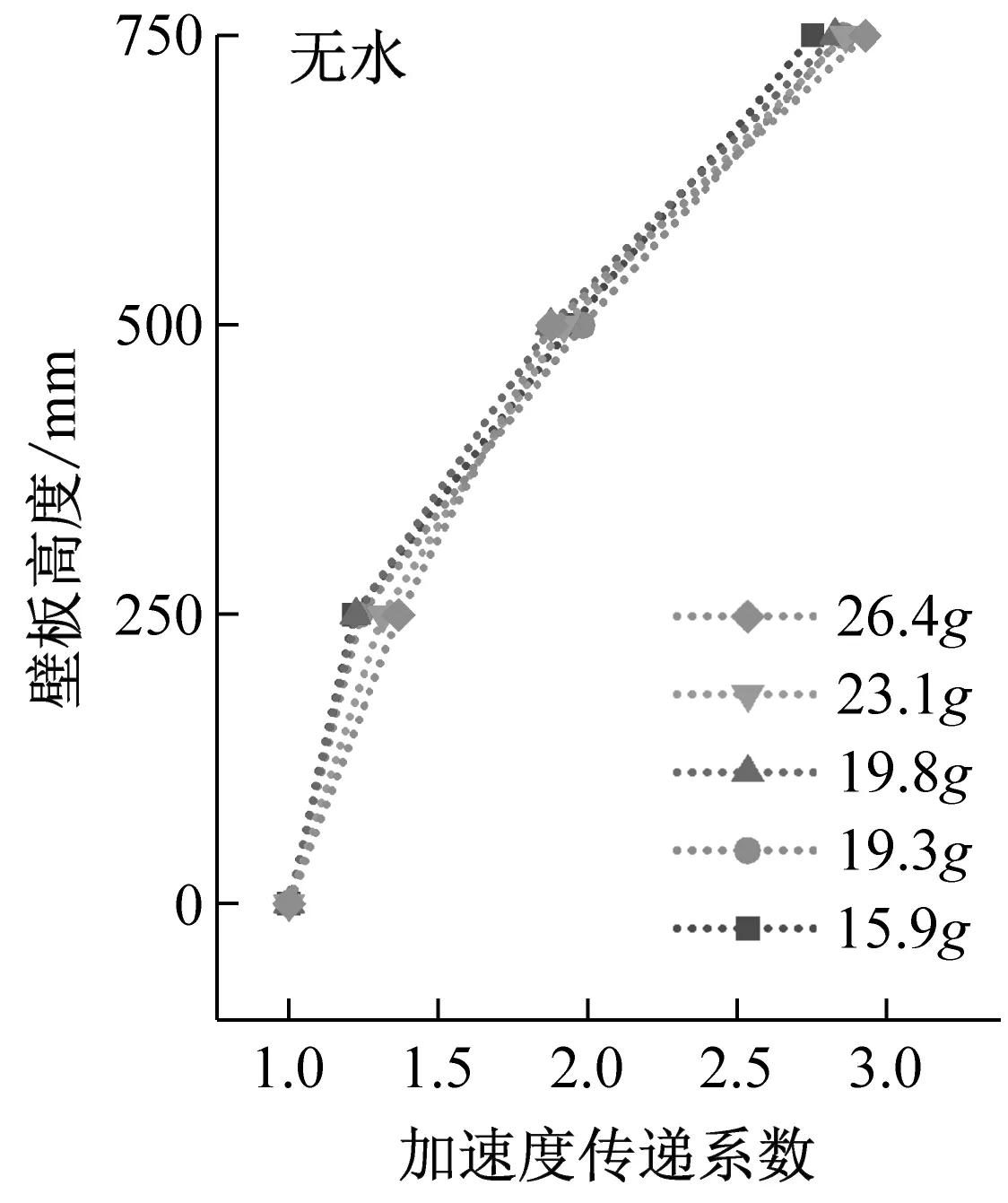
(a)

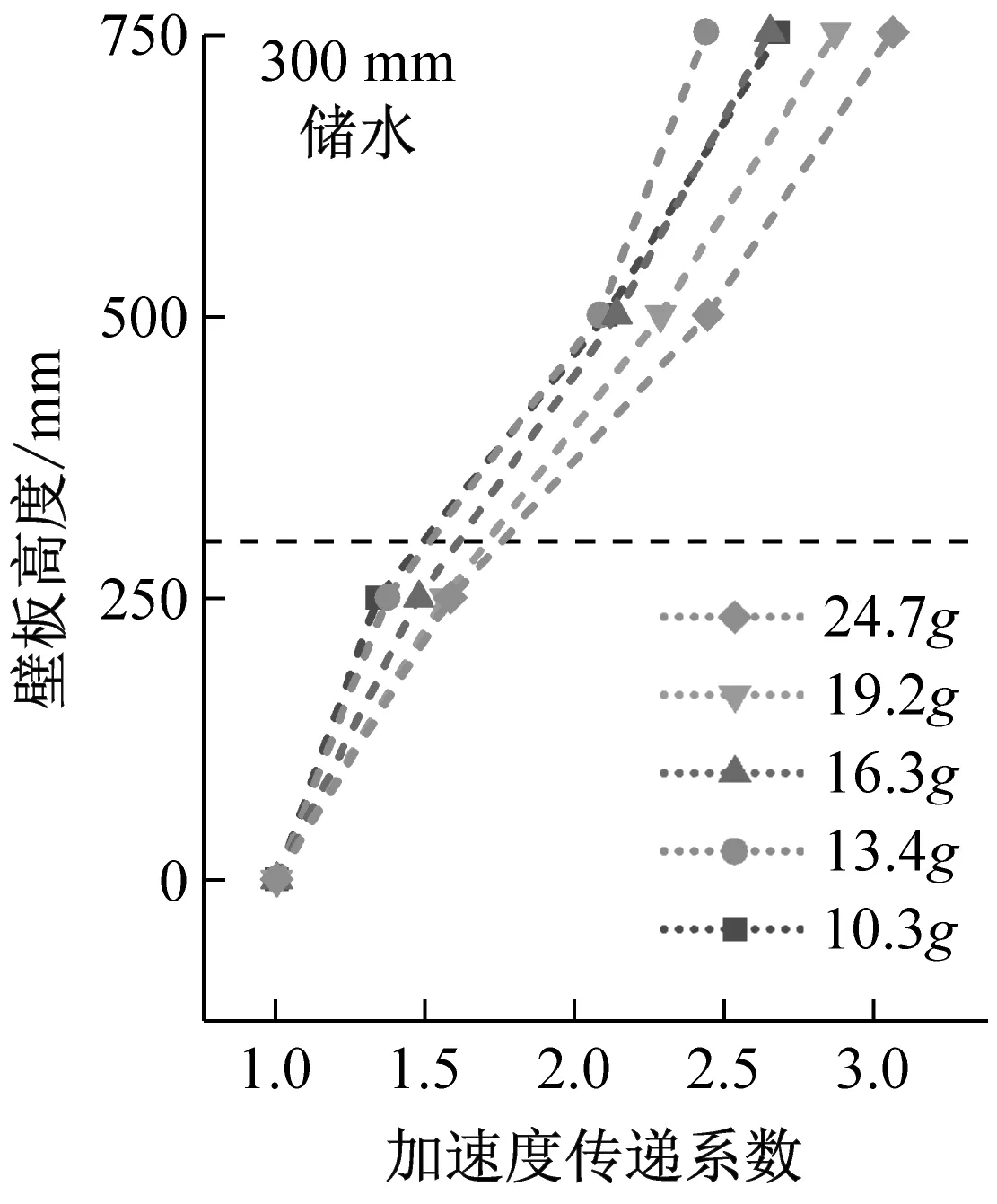
(b)

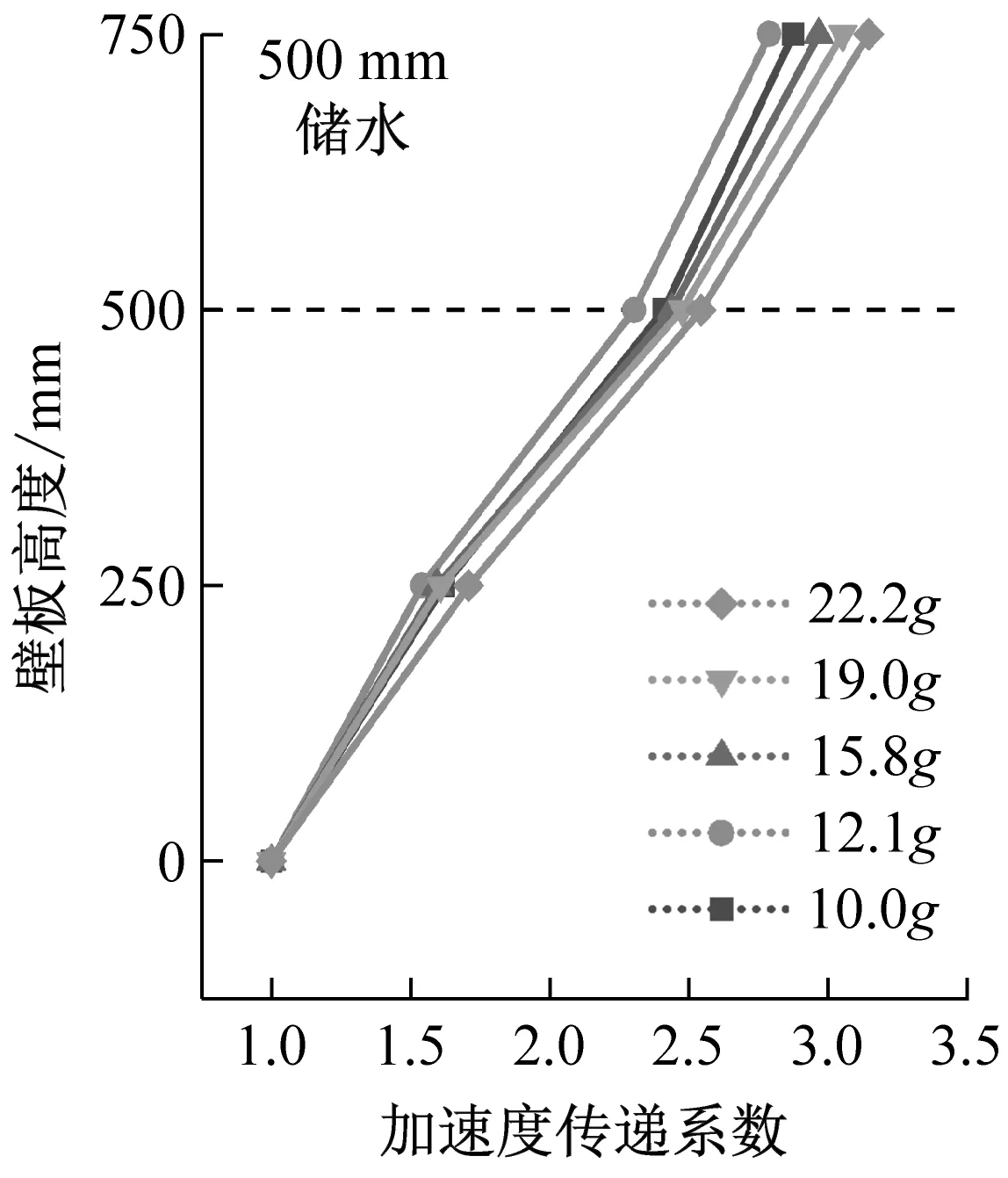
(c)圖10 結構加速度傳遞系數沿壁板高度變化Fig.10 Acceleration transfer coefficient varies along the height of the wall

不同工況下，結構加速度傳遞系數隨輸入加速度變化曲線，如圖11所示。總的來說，不同儲水條件下，隨著輸入加速度的增大，結構振動加速度放大效應均得到一定提高。無水條件下，曲線變化較平緩，說明隨著輸入加速度的增加，結構加速度傳遞系數增幅不大；儲水條件下，曲線斜率增加，說明結構加速度傳遞系數受輸入加速度的影響增大，地震動強化效應更加明顯。為了直觀體現儲液狀態對加速度傳遞系數的影響，定義16.0g等級輸入加速度(無水15.9g、300 mm儲水16.3g、500 mm儲水15.8g)和19.2g等級輸入加速度(無水19.3g、300 mm儲水19.2g、500 mm儲水19.0g)，該兩種等級輸入加速度下加速度傳遞系數隨儲水狀態變化規律，如圖12所示。由圖12可知，同一強度等級地震動加載條件下，隨著儲液深度的增加，不同測點的結構振動加速度放大效應均得到增強。

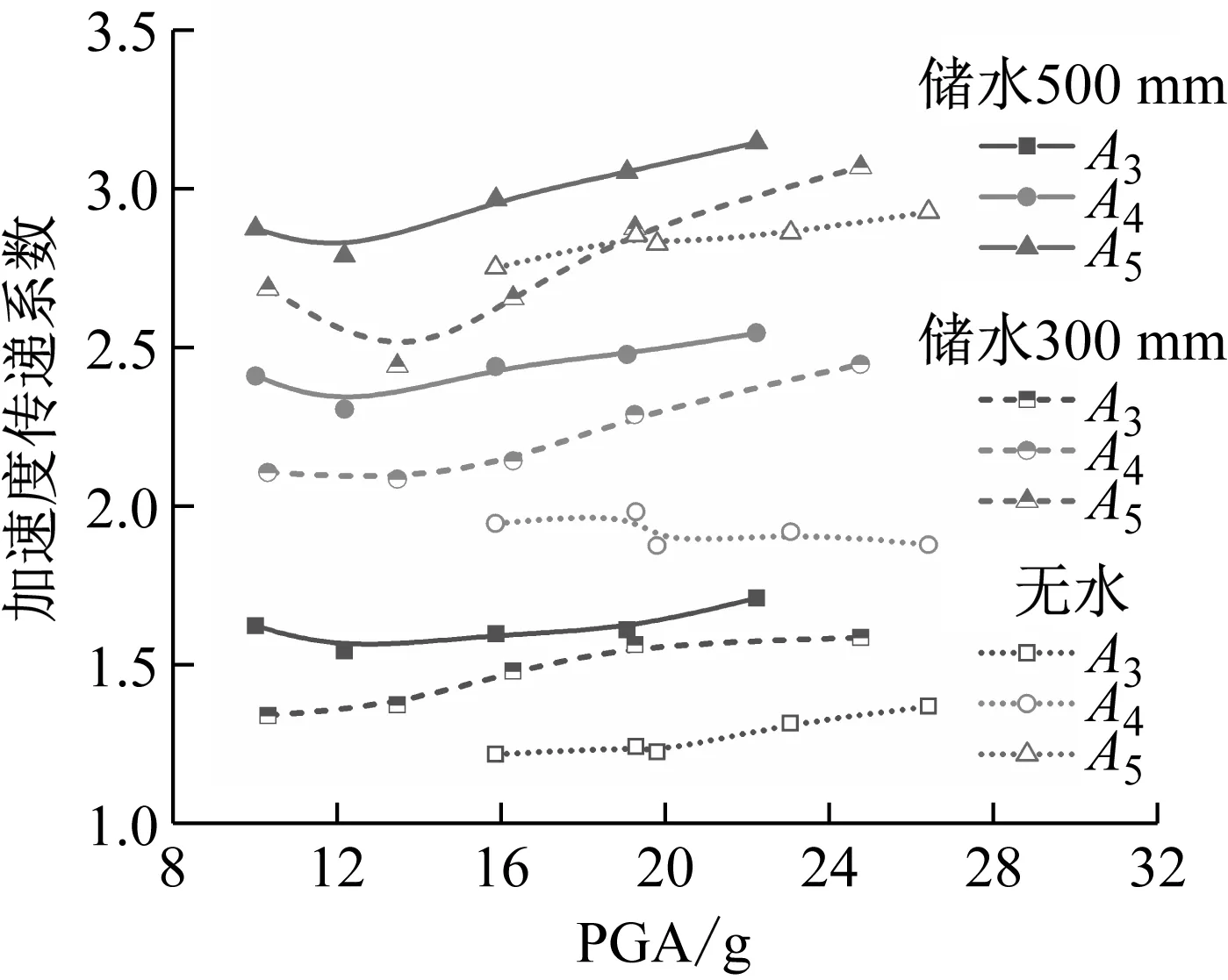
圖11 結構加速度傳遞系數隨輸入加速度變化Fig.11 Acceleration transfer coefficient varies with the input acceleration

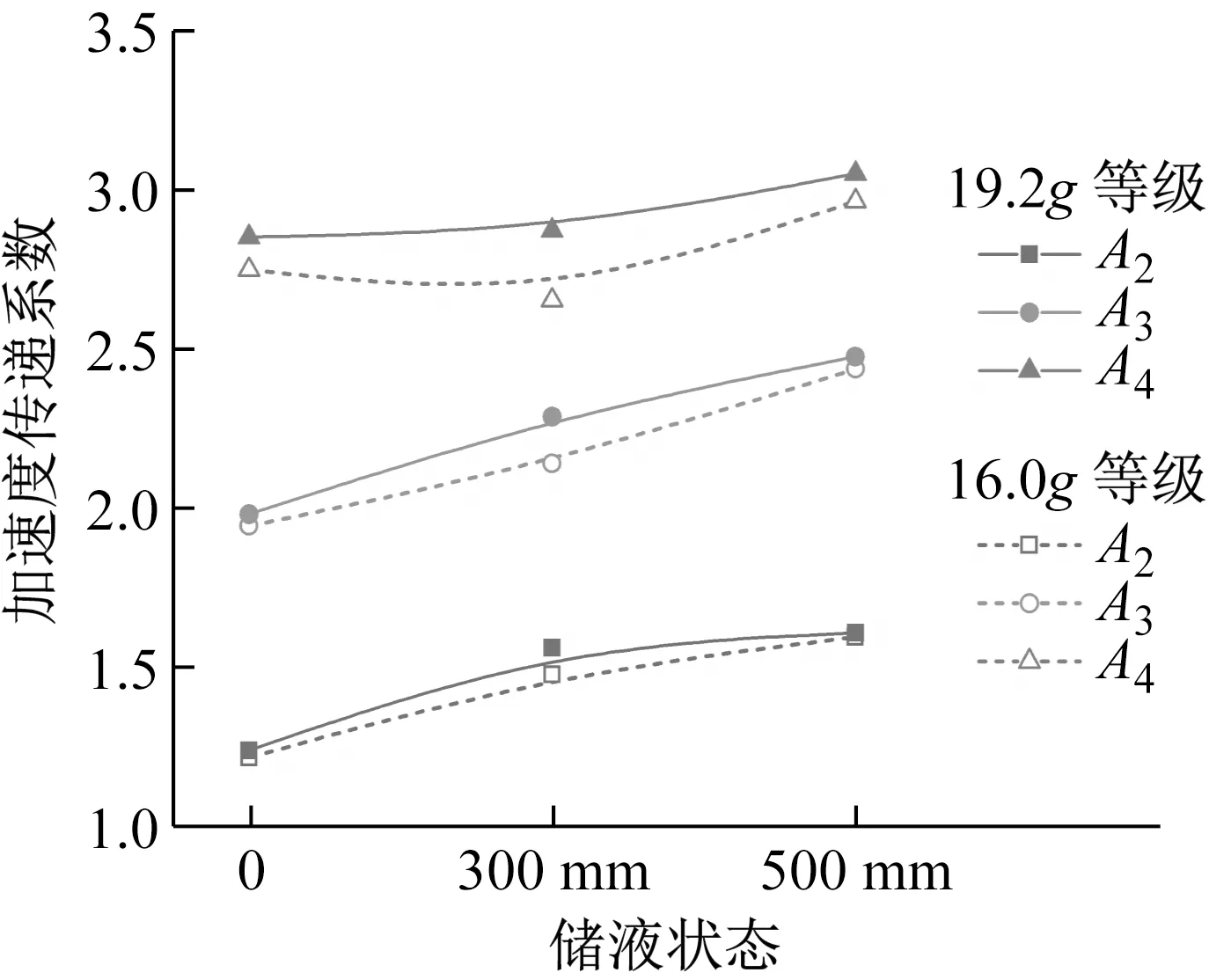
圖12 結構加速度傳遞系數隨儲液狀態變化Fig.12 Acceleration transfer coefficient varies with the liquid storage conditions

2.3 結構應變響應分析

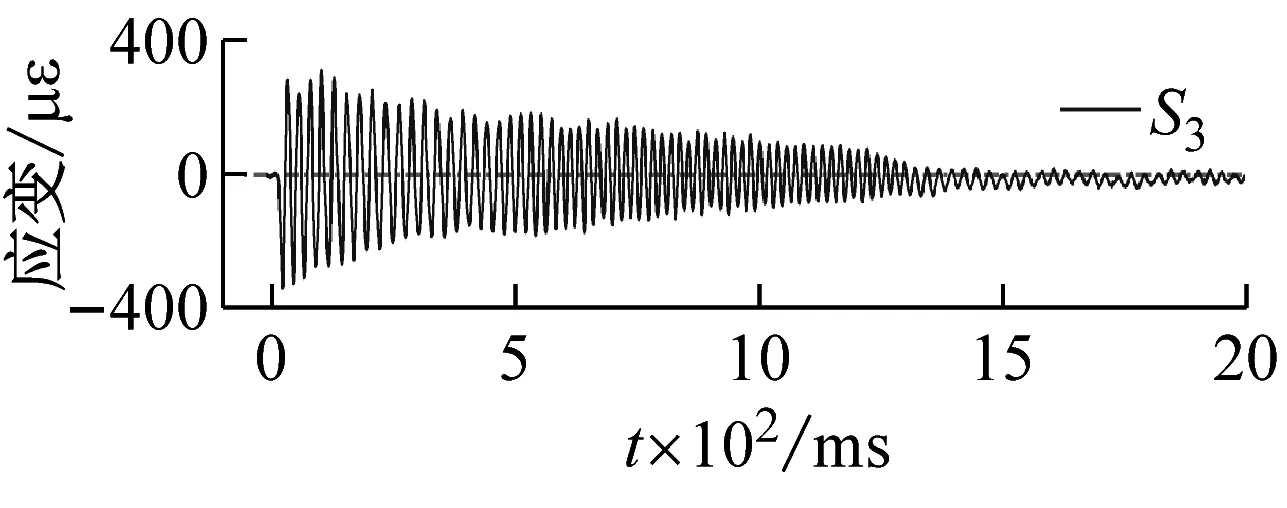
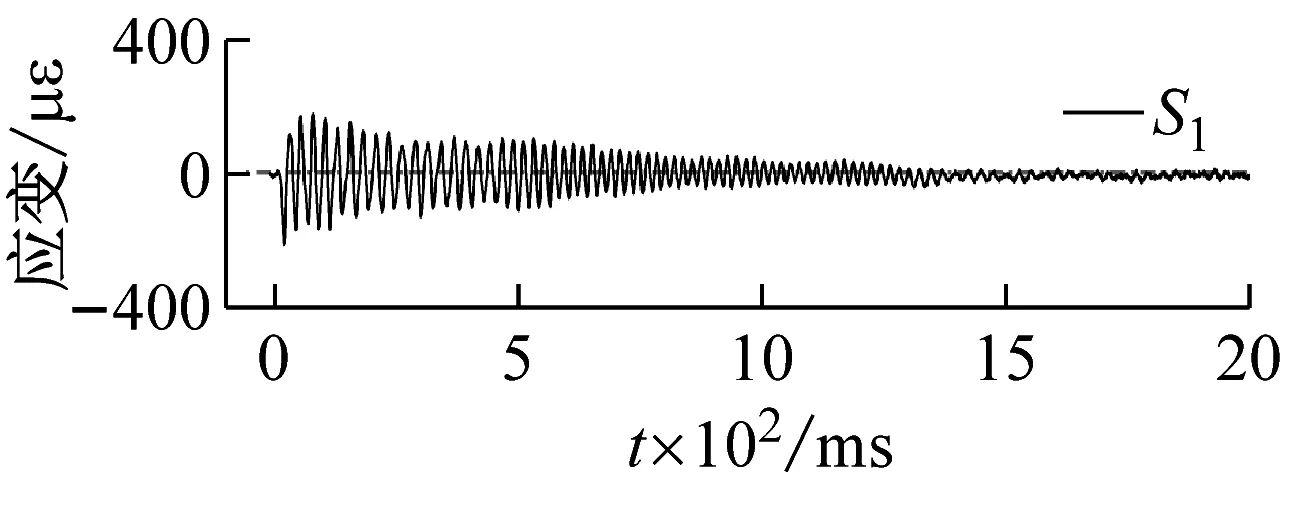
500 mm儲水、15.8g加載條件下，測點S1，S2，S3處應變響應時程曲線，如圖13所示，可以發現，受沖擊荷載后結構迅速達到最大變形，經阻尼消耗能量，往復振動變形幅值逐漸減小。加載后120 ms內不同測點處應力隨時間變化的規律，如圖14所示，可以看出，不同測點處應變的變化趨勢基本一致，由于應變片布置于結構內側，故加載后應變首先達到負向極值，即結構振動變形首先呈現內側受壓、外側受拉的狀態。

(a)

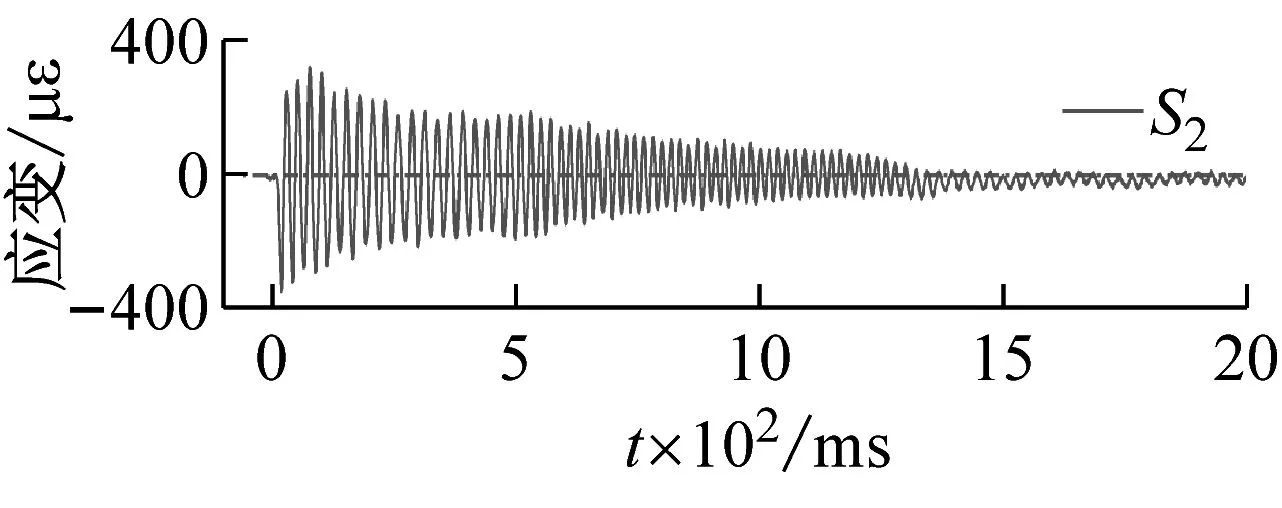
(b)

(c)圖13 應變響應典型時程曲線Fig.13 Typical time history curve of strain response

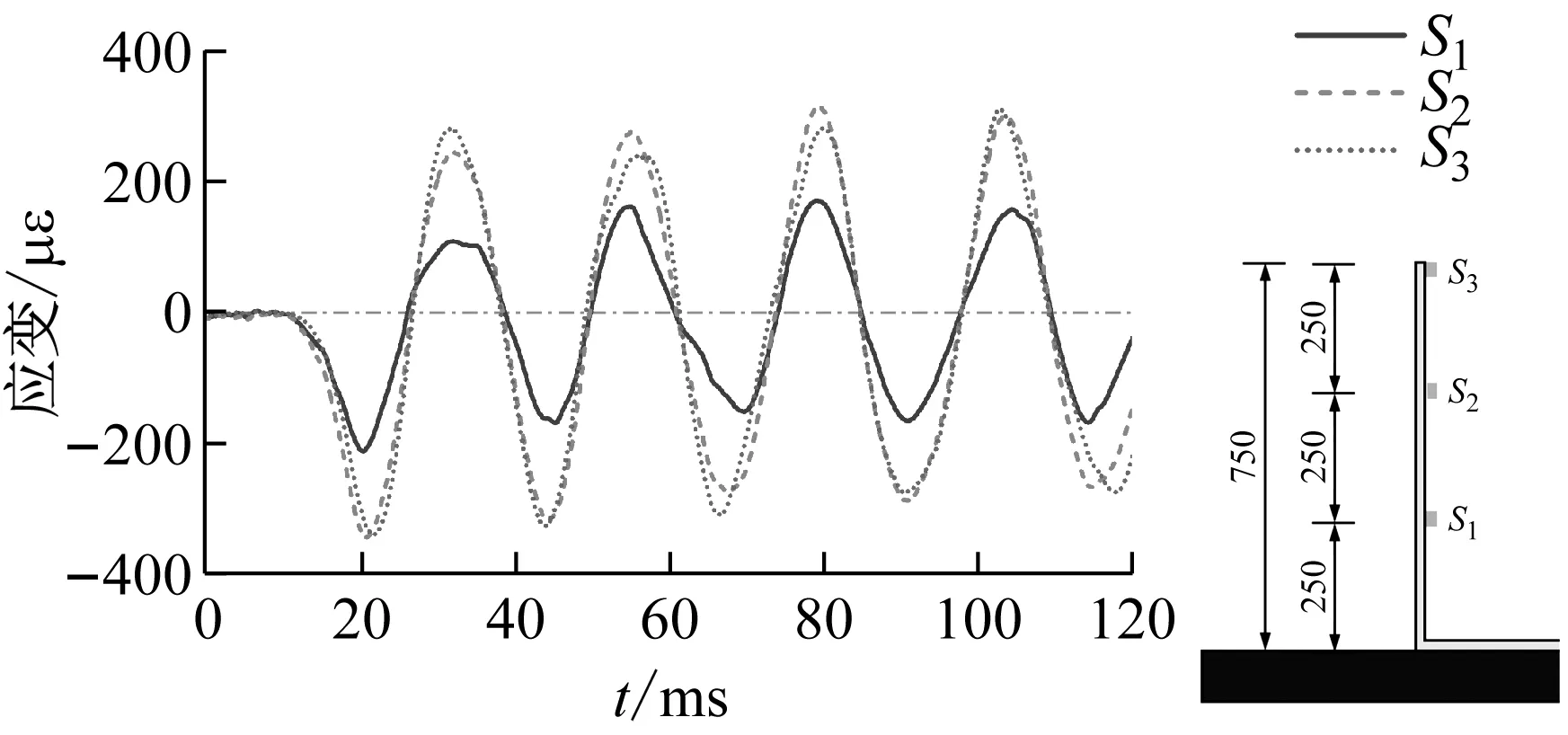
圖14 不同測點處應變規律對比Fig.14 The comparison of the law of strain response

不同儲液深度、不同輸入加速度下結構應變峰值沿壁板高度變化情況，如圖15所示。可以反映出，加載過程中結構動態應力壁板底部至頂部呈現減速增大的趨勢，在結構頂部達到最大值。相比于無水結構，儲水結構應變分布發生變化，液面以下應變增速提高，液面以上應變增速降低，當儲液深度達到500 mm時，結構頂部S3測點處應變與500 mm高度S2測點處應變相差不大。

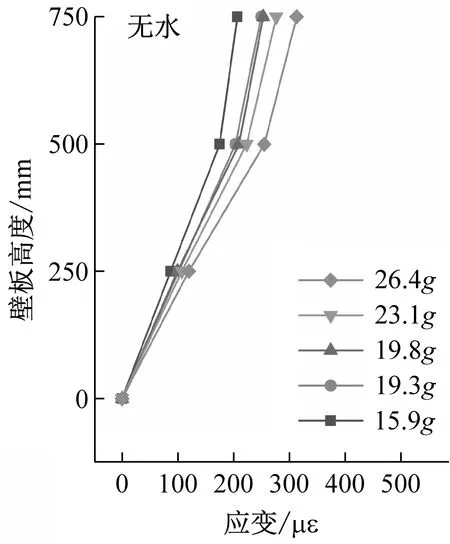
(a)

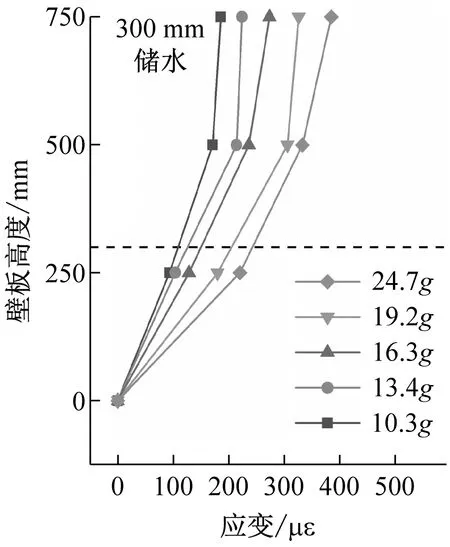
(b)

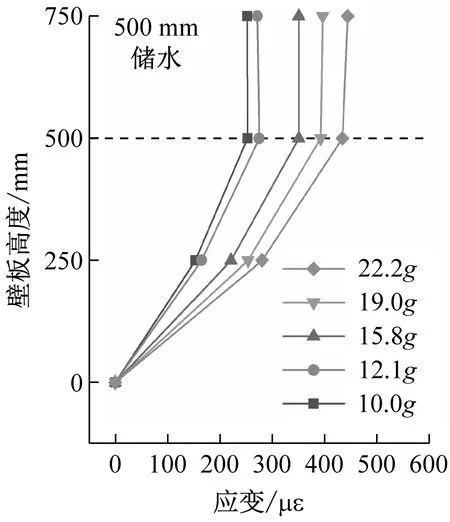
(c)圖15 結構應變峰值沿壁板高度變化Fig.15 Peak strain varies along the height of the wall

不同儲水條件下，結構應變隨輸入加速度變化曲線，如圖16所示。由圖16可知：隨著輸入加速度的提高，結構應變響應逐漸增大，其中結構頂部增幅更加明顯；與無水條件相比，儲水條件下曲線斜率增大，說明應變對于地震動強度變化的敏感性提高。16.0g等級和19.2g等級輸入加速度下，結構應變隨儲液狀態變化，如圖17所示，說明在同一等級地震動加載條件下，儲液深度的增加使結構變形值增大。以19.2g輸入加速度為例，無水、300 mm儲水、500 mm儲水條件下結構頂部最大應變值分別提高30.4%，45.9%。

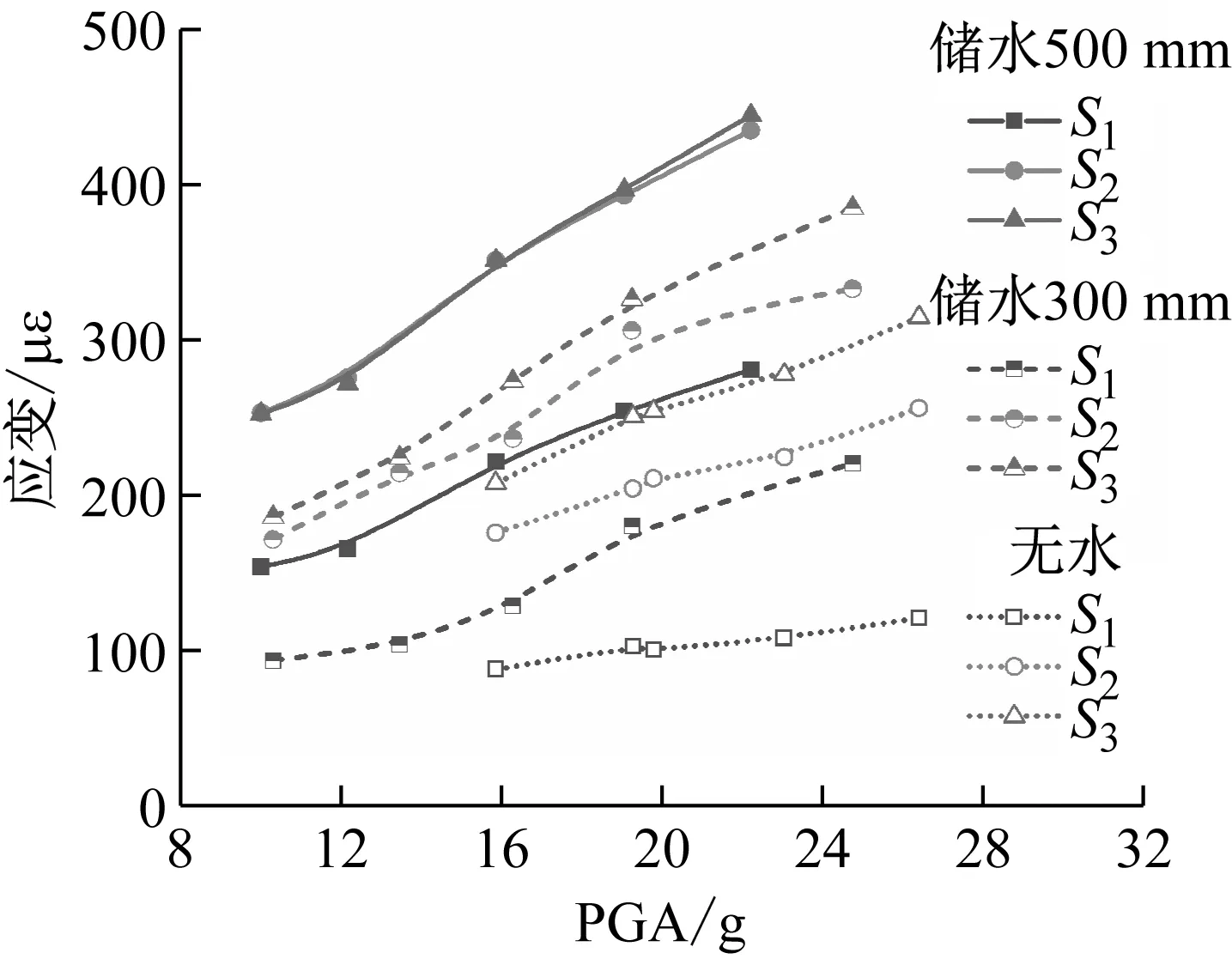
圖16 結構應變峰值隨輸入加速度變化Fig.16 Peak strain varies with the input acceleration

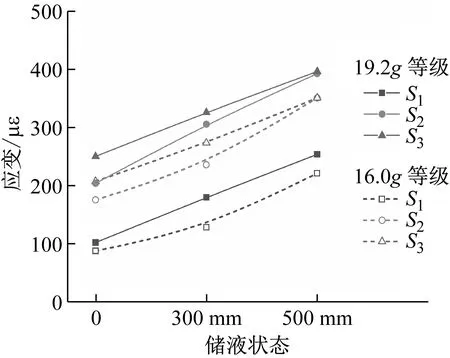
圖17 結構應變峰值隨儲液狀態變化Fig.17 Peak strain varies with the liquid storage conditions

2.4 結構動水壓力響應分析

由2.2節、2.3節分析可知，儲液狀態對于儲液結構的動力響應影響很大，動水壓力是關鍵因素。500 mm儲水、15.8g加載條件下，測點P1，P2，P3處動水壓力響應時程曲線，如圖18所示。由圖18可知，受沖擊荷載后作用于結構壁板的動水壓力迅速達到峰值，隨著結構振動衰減，動水壓力幅值逐漸減小。此外，在800～1 000 ms段，動水壓力傳感器監測到的響應值為零，這是由于爆炸沖擊震動模擬平臺缺少限位裝置，振動臺晃動致結構內儲液體流向對側壁板。加載后120 ms內不同測點處動水壓力隨時間變化的規律，如圖19所示。由圖19可知，由結構底部P1測點至上部P3測點，動水壓力首個峰值依次出現，說明動水壓力響應自結構底部向頂部傳遞的過程中產生了相位差。

(a)

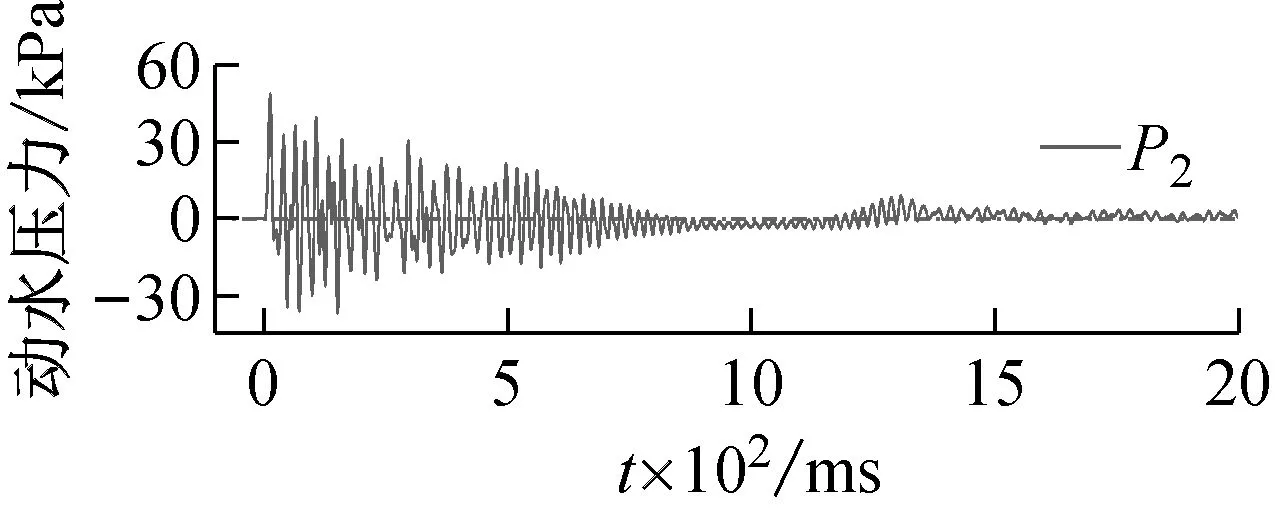
(b)

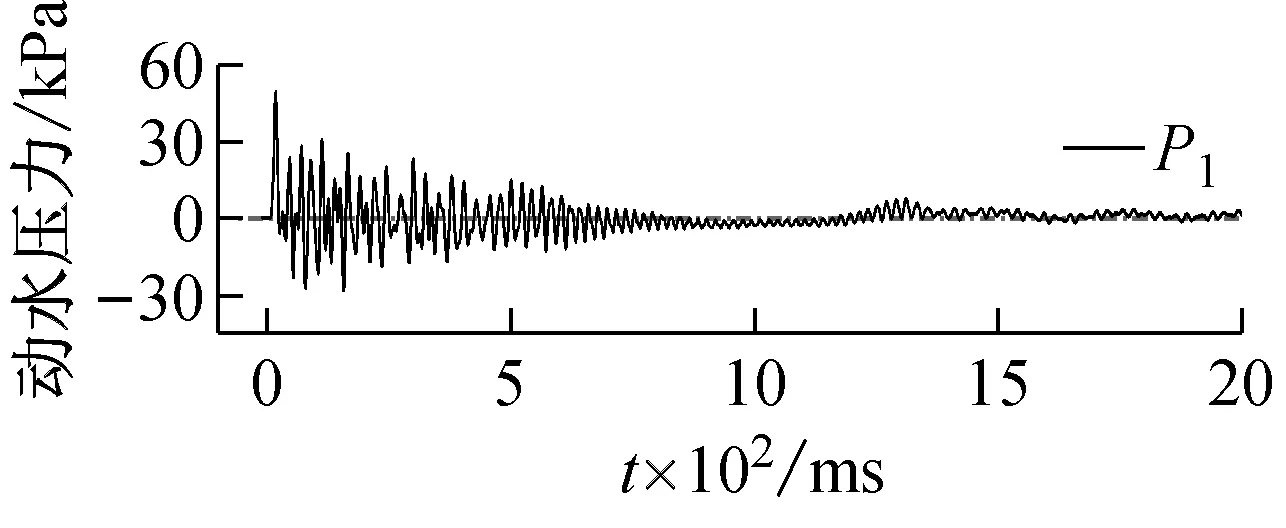
(c)圖18 動水壓力響應典型時程曲線Fig.18 Typical time history curve of hydrodynamic pressure

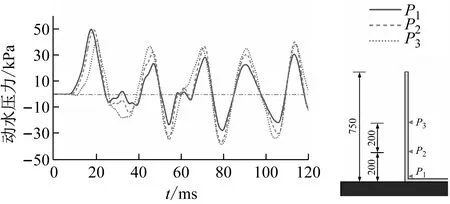
圖19 不同測點處動水壓力規律對比Fig.19 The comparison of the law of hydrodynamic pressure

不同儲液深度、不同輸入加速度下結構動水壓力峰值沿壁板高度變化情況，如圖20所示。由圖20可知，在500 mm儲水條件下，動水壓力隨水深增加表現出減速增大的趨勢，結構底部動水壓力最大，而2/5水位處與結構底部動水壓力相差不大，結構臨水部分中下段承受了水平相當且幅值較高的動水壓力。

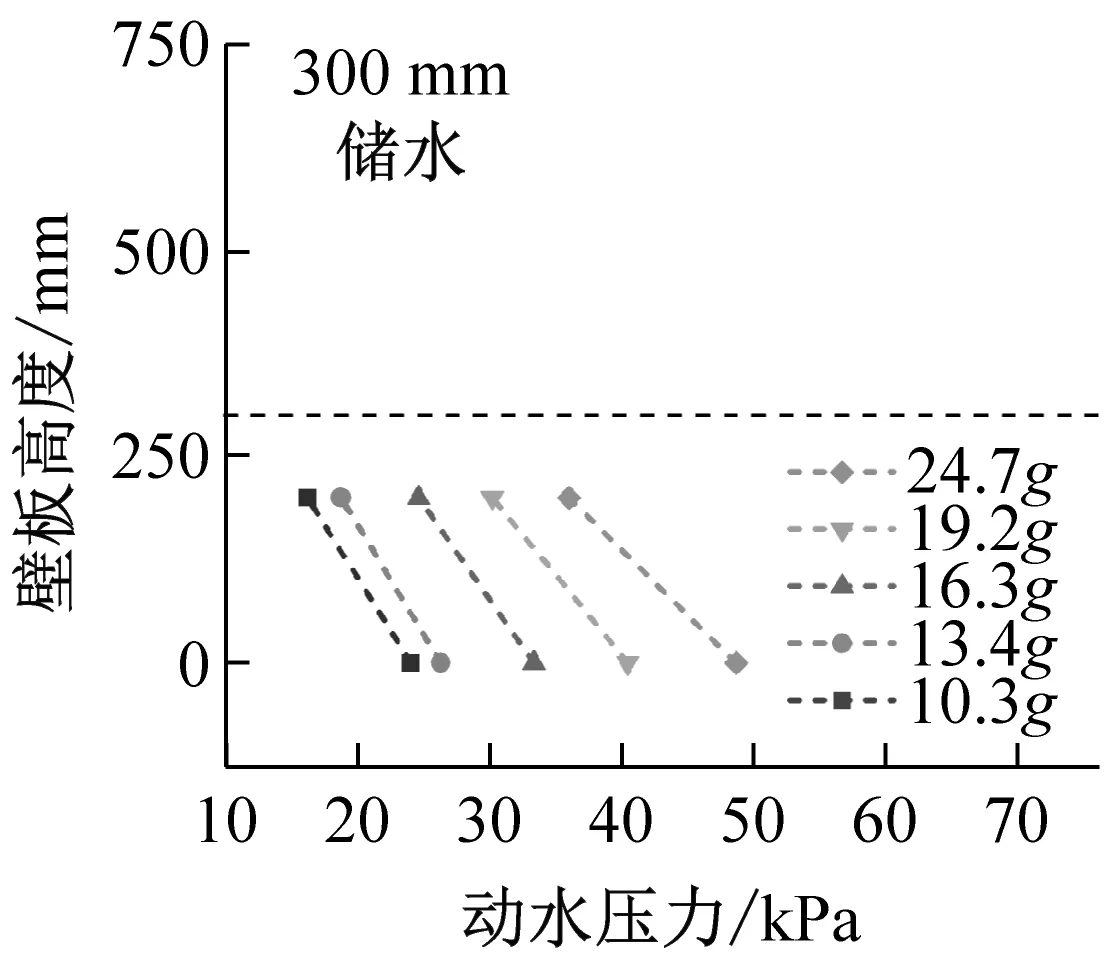
(a)

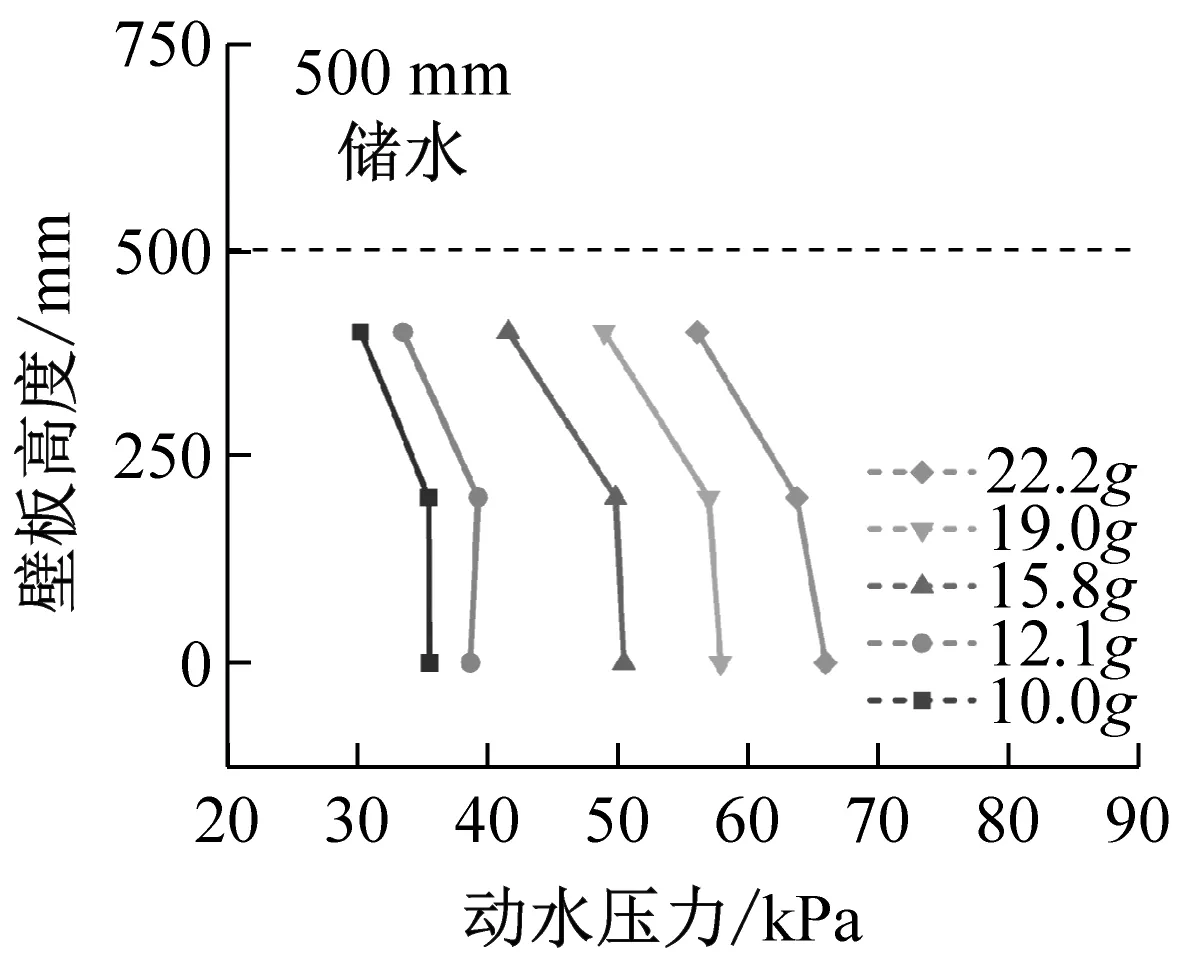
(b)圖20 結構動水壓力沿壁板高度變化Fig.20 Hydrodynamic pressure varies along the height of the wall

不同工況下，結構動水壓力隨輸入加速度變化曲線，如圖21所示。由圖21可知：隨著輸入加速度的增加，結構承受的動水壓力逐漸增大；結構儲水由300 mm增至500 mm，在不同加速度加載的條件下，動水壓力均有明顯的增幅。

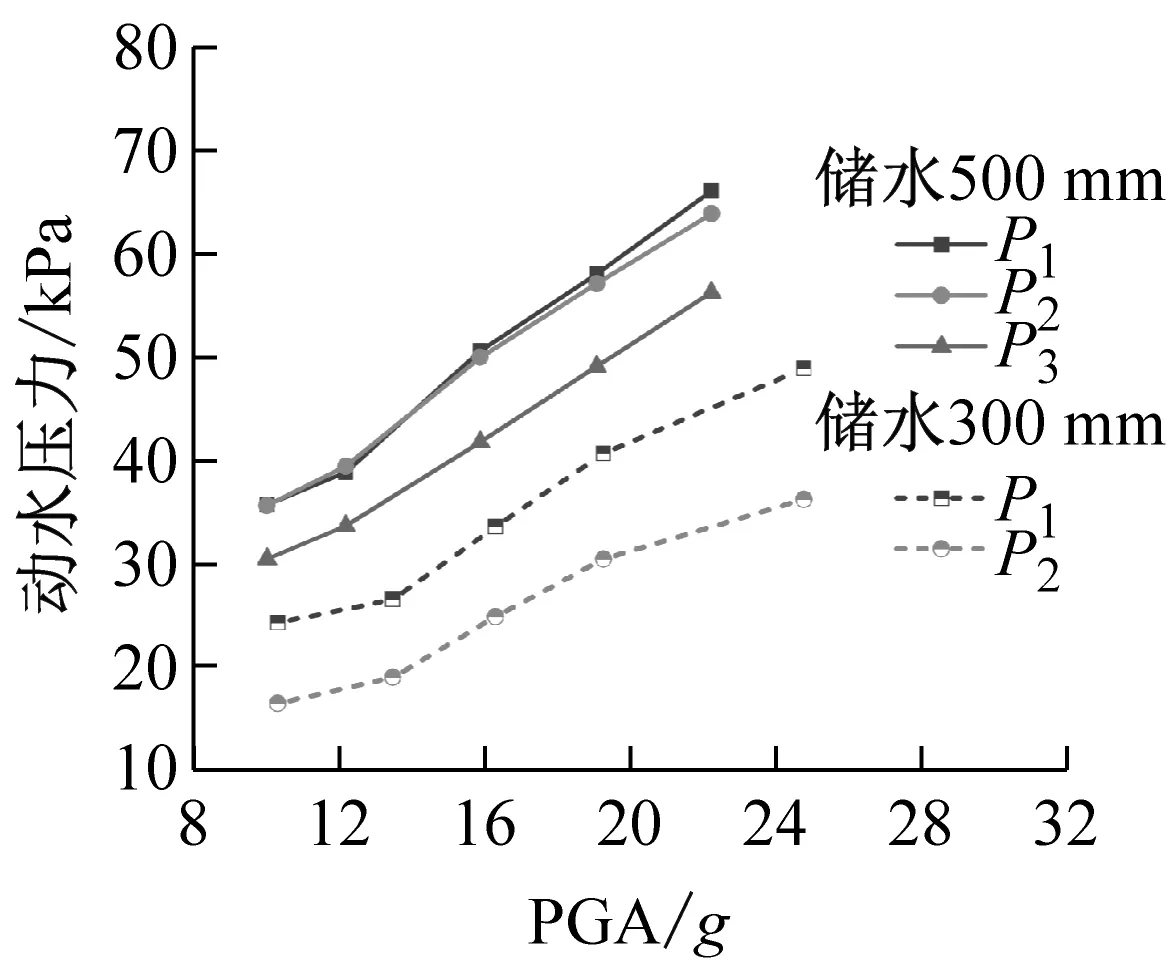
圖21 結構動水壓力隨輸入加速度變化Fig.21 Hydrodynamic pressure varies with the input acceleration

3 理論分析與討論

3.1 儲液結構壁板振型探討

由引言部分可知，以往學者對于儲液結構自振特性開展了相關研究，關于壁板振型尚未得到一致結論。本文基于試驗數據，對于儲液結構壁板振型進行初步的探討。儲液結構計算模型示意圖如圖22所示，圖22中：地震動沿x方向；Lx為矩形儲液結構沿地震作用方向的邊長；Ly為結構垂直地震作用方向的邊長；Hs為結構高度；Hw為儲液深度。

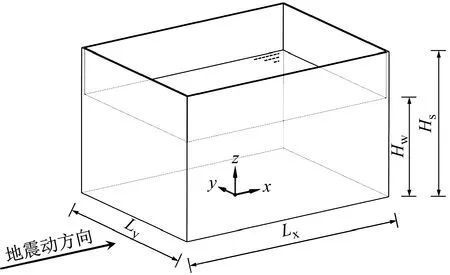
圖22 儲液結構計算模型示意圖Fig.22 Schematic diagram of LSS calculation model

由板殼振動理論[33]可知，矩形板固有振動分析可采用雙向梁函數組合級數逼近方法，一般性矩形薄板的撓度振型W(y,z)可表示為

(3)

式中：Ym(y)與Zn(z)分別為與壁板水平y方向，豎直z方向兩端邊界條件對應的第m與n階梁振型函數；Amn為待定系數，用于調整梁函數的組合以逼近矩形板振型真實解。矩形薄板的振動方程w(y,z,t)可表示為

w(y,z,t)=W(y,z)T(t)

(4)

式中，T(t)為時間相關的動力函數。因此，得到板內橫向應變分量εy為

(5)

將式(3)、式(4)代入可得

(6)

式中，t為壁板厚度。考慮到試驗中單向應變片沿壁板水平y方向布置，且均粘貼處于壁板中軸位置(y=0)，故由式(6)可知S1，S2，S3測點應變值對比結果為

εy(S3):εy(S2):εy(S1)=Zn(S3):Zn(S2):Zn(S1)

(7)

該結果反映了結構壁板豎向振型。因此，將圖15應變測量結果進行歸一化處理，結果如圖23所示。

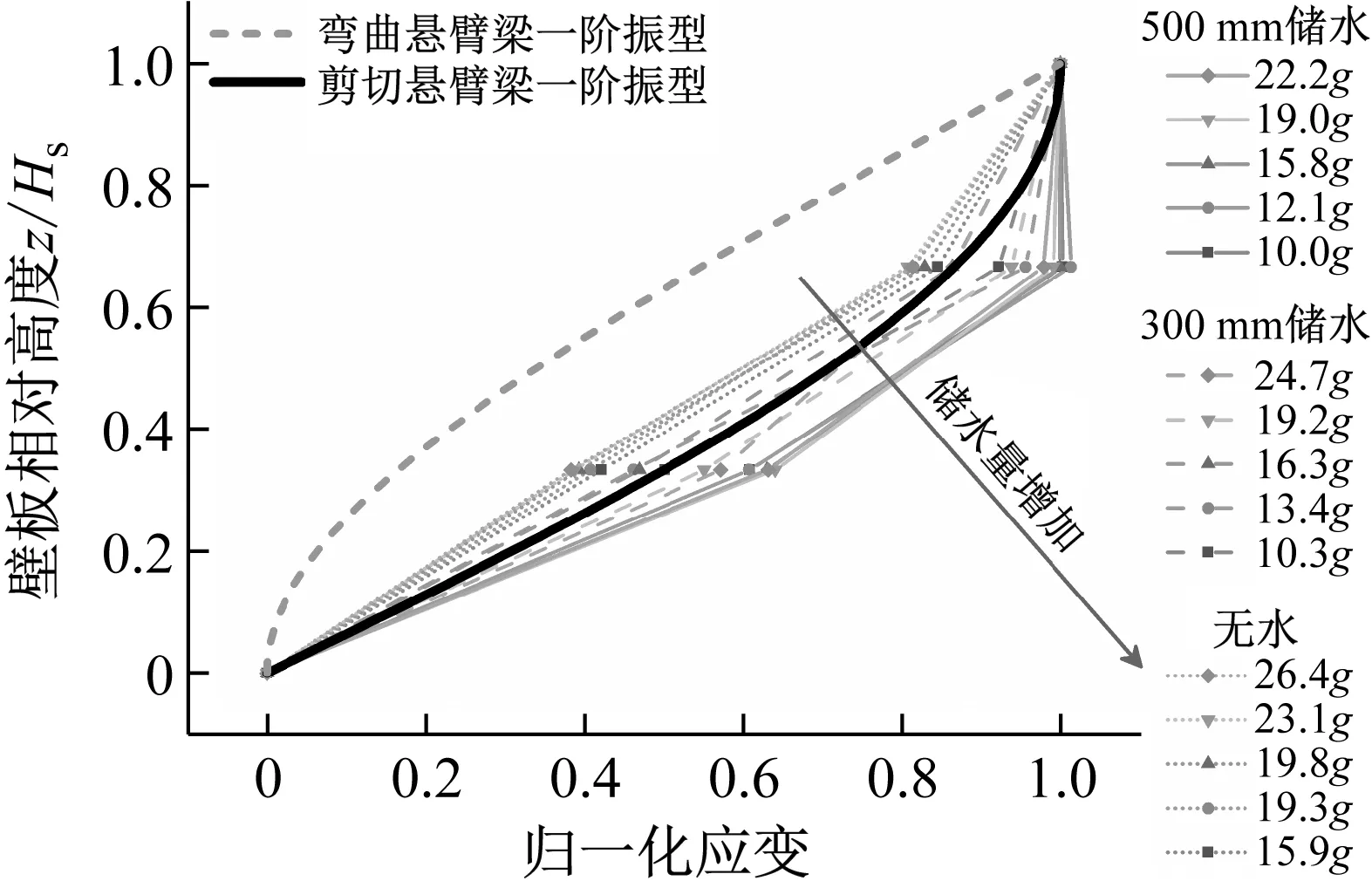
圖23 結構應變峰值沿壁板高度變化歸一化結果Fig.23 Normalized results of peak strain along the height of wall

圖23中除歸一化的試驗數據外，標注了彎曲懸臂梁一階振型曲線與剪切懸臂梁一階振型曲線。可以看出，不同工況下試驗值與剪切懸臂梁振型曲線更接近，說明儲液結構壁板振動豎向振型更加符合剪切型變形理論。由無水至300 mm儲水、500 mm儲水，液體附加質量效應出現并逐漸增強，壁板振型在剪切懸臂變形的基礎上發生局部變化，表現為液面以下壁板臨水部分變形得到增強，上部無水部分變形相對弱化。

3.2 動水壓力理論計算與規范對比

考慮到動水壓力對于儲液結構動力響應的重要影響，抗震設計時需對爆炸地震動下的動水壓力進行驗算。首先進行理論方法求解，計算模型參考圖22。基于程選生等推導的動水壓力計算方法，在考慮儲液結構彈性變形的條件下，壁板受到的脈沖動水壓力pi由兩部分組成：剛體運動產生的脈沖壓力pg與考慮壁板側向變形產生的脈沖壓力pf，可按式(8)～式(11)計算

(8)

(9)

(10)

(11)

(12)

式中，βmax為單質點彈性結構的最大水平加速度與地震動最大加速度的統計平均值的比值[34]，即

(13)

對于鋼筋混凝土儲液結構取值2.25。對于本文不銹鋼儲液結構，以2.2節加速度傳遞系數統計平均值進行修正，取為2.85。

此外，基于Hashemi等提出的流固耦合理論方法，壁板對流壓力pc可按式(14)～式(19)計算

(14)

(15)

(16)

λj=(2j+1)π/2

(17)

αj=λj/Lx

(18)

(19)

以500 mm儲水、擺錘高度H3工況為例，通過Maple軟件進行理論計算前，以Asym2Sig模型[見式(20)]對地震動加速度信號進行單峰值擬合，結果如圖24所示，擬合曲線與試驗曲線吻合較好。

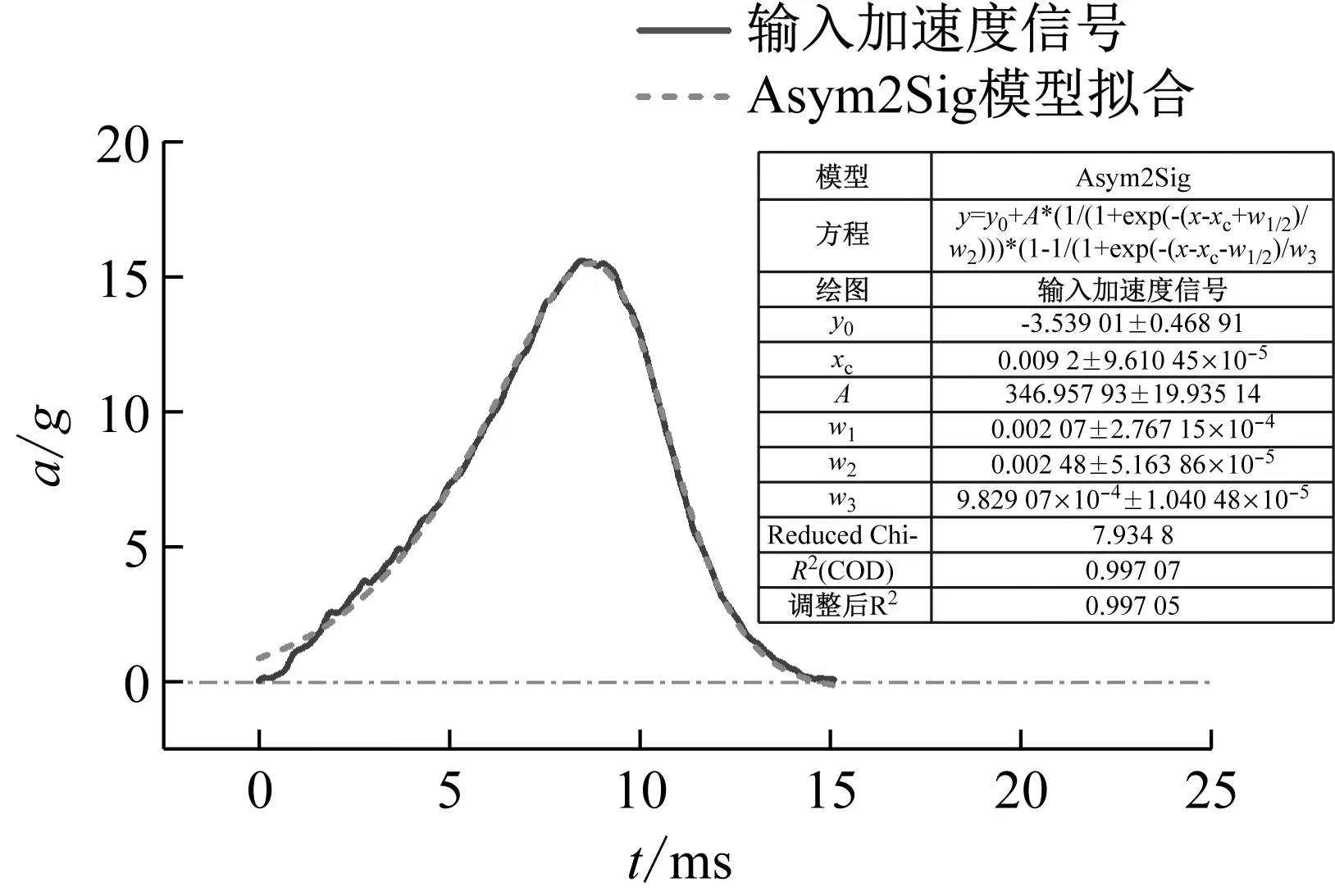
圖24 典型輸入加速度信號與Asym2Sig模型擬合結果Fig.24 The typical input acceleration signal and the fitting results using Asym2Sig model

(20)

將擬合函數代入式(8)～式(19)，計算得到該工況下動水壓力理論值，計算結果如圖25～圖26所示。圖25中呈現了地震動加速度峰值時刻脈沖壓力pi、剛體運動脈沖壓力pg、壁板變形脈沖壓力pf、以及對流壓力pc沿臨水壁板分布情況。可以看出：液面以下隨著水深增加，pi，pf先增大后減小；pg逐漸增大，在結構底部達到最大值；pc逐漸減小，最大值出現在液面處。相比之下，液體晃動產生的對流壓力不足脈沖壓力的1%，對動水壓力影響可忽略。脈沖壓力則是動水壓力主要組成部分，對儲液結構動力響應起主要作用。

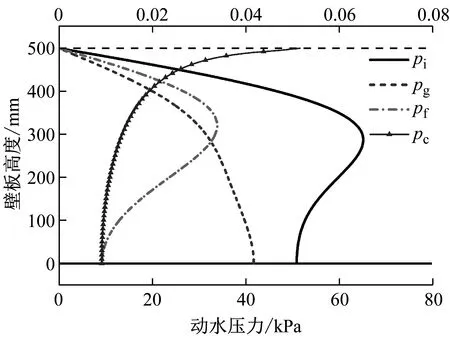
注：脈沖壓力pi,pf，pg參照下軸；對流壓力pc參照上軸。圖25 理論計算動水壓力沿壁板分布Fig.25 Theoretically calculated hydrodynamic pressure distribution along the wall

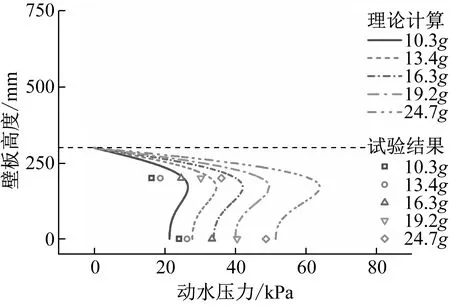
(a) 300 mm儲水

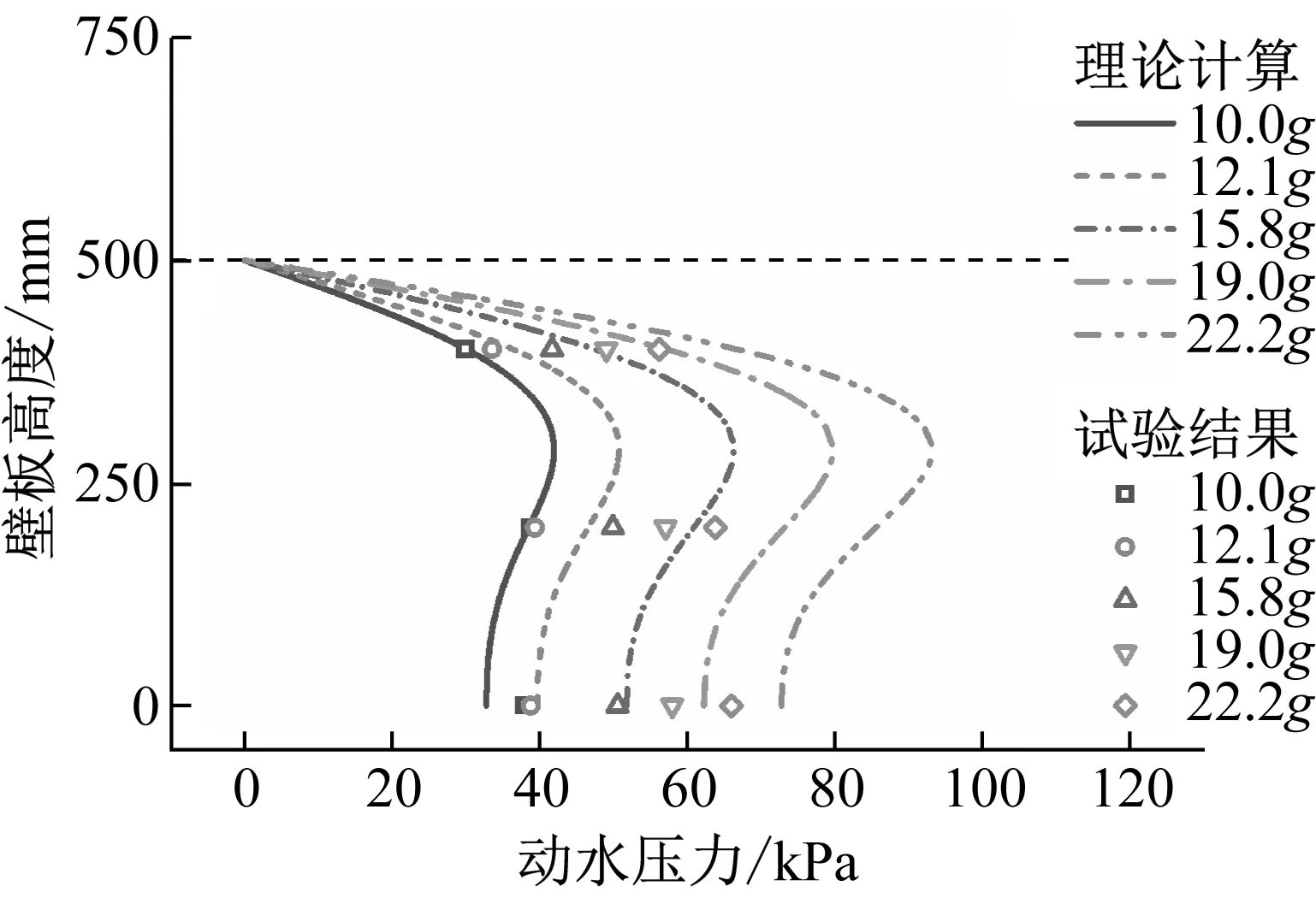
(b) 500 mm儲水圖26 動水壓力理論計算與試驗結果對比Fig.26 Comparisons between theoretical calculations and experimental results of hydrodynamic pressure

對比不同測點處動水壓力最大值理論計算與試驗結果，如圖26所示。可以發現兩者存在一定偏差，分析其原因，一是式(8)～式(11)計算pg與pf時對結構振型進行簡化，弱化了結構響應的非線性；二是式(12)計算pi時作了簡化處理，以便于工程設計。但總的來說，理論計算值在結構底部P1，上部P3處吻合較好，不同測點處計算偏于保守，有利于結構安全設計。加之工程設計往往關注計算求解的便利性，上述理論計算方法仍具有較好的適用性，下面結合現有設計規范進行討論。

現行規范中提供了盛水構筑物動水壓力的抗震驗算方法。其中，GB 50032—2003《室外給水排水和燃氣熱力工程抗震設計規范》[35]在進行矩形水池抗震驗算時，將壁板受到的動水壓力簡化為沿平面、沿高度等值分布，并給出地面式矩形水池在水平地震作用下動水壓力標準值Fwr,c的計算方法

Fwr,c=KH·γw·Hw·fwr

(21)

式中：KH為水平地震加速度與重力加速度的比值；γw為池水重力密度；fwr為地面式矩形水池動水壓力系數，可按表2采用。

表2 地面式水池動水壓力系數fwrTab.2 Hydrodynamic pressure coefficient of above-ground pool, fwr

參照規范計算式(21)對動水壓力理論計算式(12)進行改進，得到

Fwr,c2=KH·γw·Hw·fwr2

(22)

(23)

將式(23)進一步化簡，得到

(24)

式(24)表達了fwr2與Lx/Hw的函數關系，對應函數曲線如圖27所示。可以看出，對于本文地面式不銹鋼矩形儲液結構，GB 50032—2003《室外給水排水和燃氣熱力工程抗震設計規范》系數fwr偏差較大且不利，需要進行修正。參考規范中常見做法進行離散化處理，得到修正后的動水壓力系數fwr2取值表，見表3，可供相關工程按照線性差值法使用。

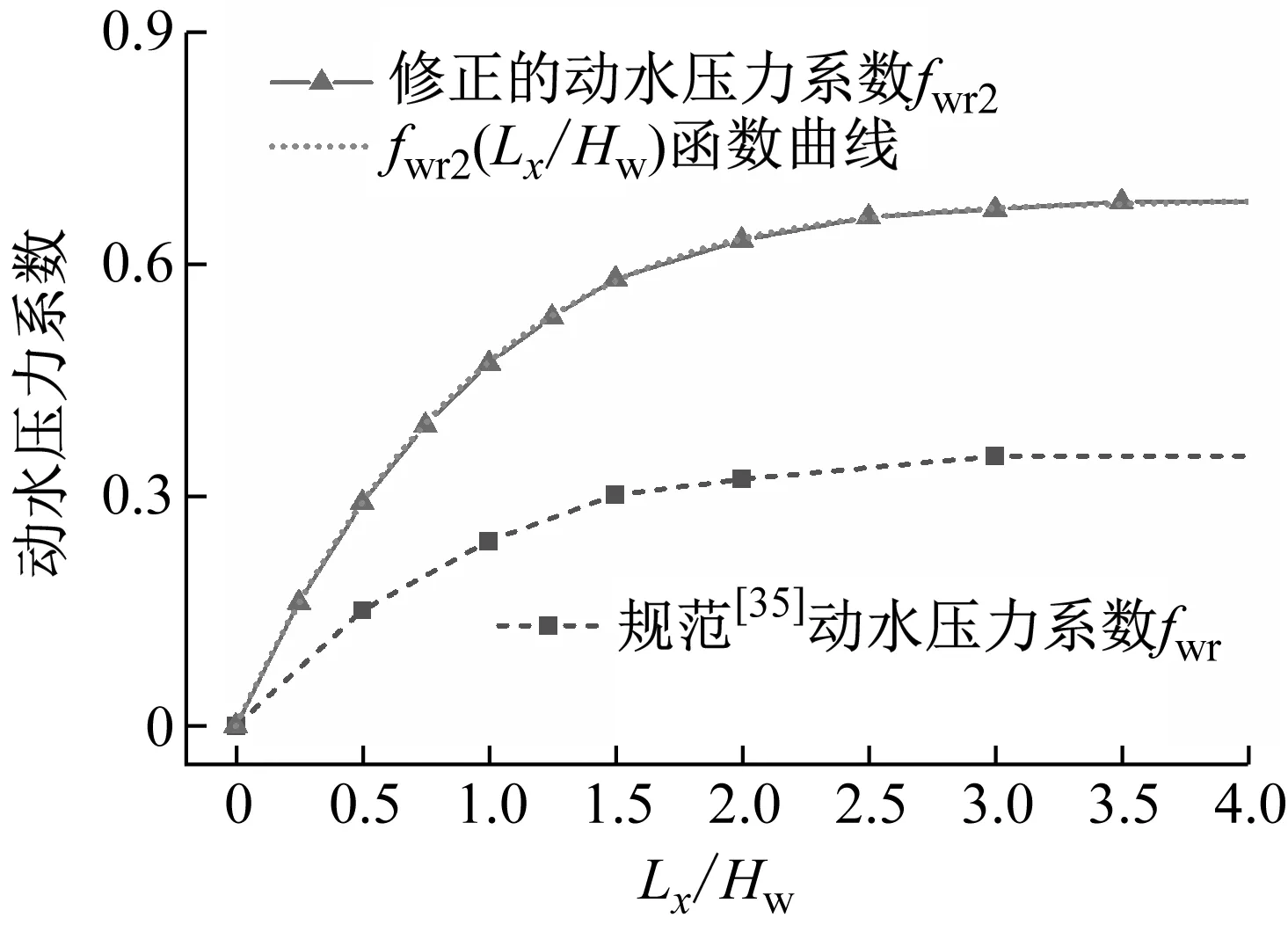
圖27 動水壓力系數修正結果Fig.27 Modified result of hydrodynamic pressure coefficient

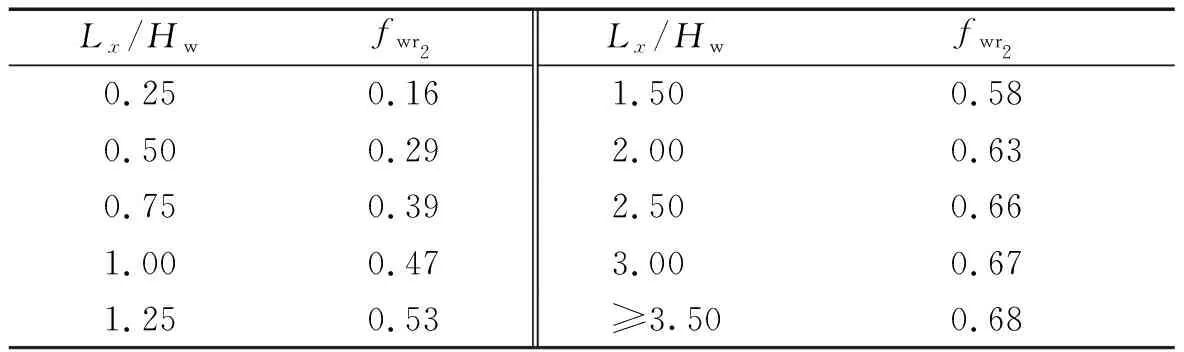
表3 修正后的地面式不銹鋼儲液結構動水壓力系數fwr2Tab.3 Modified hydrodynamic pressure coefficient for ground-mounted stainless steel rectangular LSS, fwr2

此外，在進行儲液結構抗震設計時，需要考慮動水壓力所產生的傾覆力矩。在推導動水壓力計算式的基礎上，作用于儲液結構壁板上的動水壓力所導致的傾覆力矩可計算為

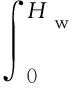
(25)

聯立式(12)并參照規范計算式(21)進行改進，得到

(26)

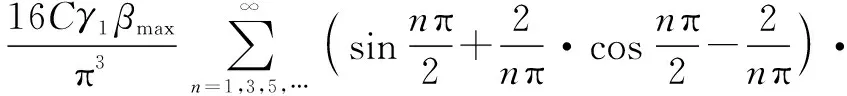
(27)

式(27)表達了傾覆力矩系數mover與Lx/Hw的函數關系，對應函數曲線如圖28所示，經離散化處理得到的動水壓力傾覆力矩系數mover取值表，見表4，可供相關工程按照線性差值法使用。

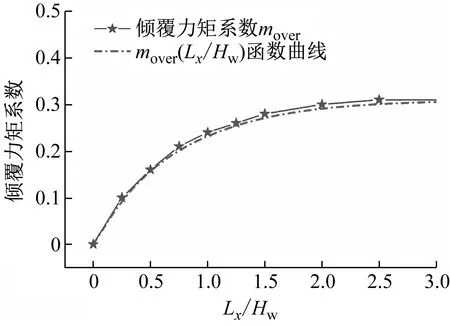
圖28 動水壓力傾覆力矩系數計算結果Fig.28 Calculation result of overturning moment coefficient

表4 地面式不銹鋼儲液結構傾覆力矩系數moverTab.4 Overturning moment coefficient for ground-mounted stainless steel rectangular LSS, mover

4 結 論

本文利用爆炸沖擊震動模擬平臺對固有頻率為54.15 Hz的地面式矩形無頂蓋儲液結構開展了動力響應試驗研究，得到了峰值加速度范圍為10.0～26.4g、平均持時為14.8 ms的地震動荷載，分析了儲液狀態、地震動強度對儲液結構動力響應的影響，結合試驗與理論方法揭示了儲液結構振型特點和動水壓力變化規律，主要結論有：

(1) 通過分析傳遞函數得到不同儲液狀態下儲液結構的固有頻率，發現儲液狀態影響液-固體系固有頻率，由無水到300 mm儲水、500 mm儲水狀態，液-固體系固有頻率分別下降9.82%，28.80%。

(2) 儲液結構振動加速度沿壁板高度呈放大效應，地震動強度的提高使放大效應更加明顯。相比于無水條件，儲水條件下加速度傳遞系數對地震動強度的敏感性提高。同一等級地震動強度下，隨著儲液深度增加，結構加速度放大效應增強。

(3) 儲液結構應變沿壁板高度呈現減速增大的趨勢，壁板振動豎向振型符合懸臂梁剪切變形理論。儲水條件下，壁板臨水部分變形由于液體附加質量效應得到加強，無水部分變形相對弱化。結構變形隨地震動增強而增加，結構頂部應變值的地震動強度敏感性較強。同一等級地震動強度下，儲水深度的增加使結構變形幅度提高。

(4) 儲液結構動水壓力隨水深增加呈現先增大后減小的趨勢，相較于對流壓力，脈沖壓力是動水壓力主要組成部分。分別以流固耦合理論方法和現行設計規范計算得到了水平地震作用下動水壓力標準值，發現現有規范對地面式矩形不銹鋼儲液結構設計不利，結合理論方法修正了動水壓力系數。推導了動水壓力所致傾覆力矩的計算公式，并得到了傾覆力矩系數。

本文采用模型試驗方法進行參數研究，并結合理論分析得到了一些結論。未來還需要對針對不同結構尺寸、形狀等進一步研究，以擴充認知體系，得出更具普遍指導意義的結論。