基于機電耦合動力學的3K行星輪系裂紋故障電流信號研究

桑 萌， 黃 康， 熊楊壽

(1.合肥工業大學 機械工程學院，合肥 230009；2.安徽省數字設計與制造重點實驗室，合肥 230009)

行星齒輪傳動因其結構緊湊、傳動比大、傳動效率高等特點，適用于高速大功率以及低速大扭矩的傳動場景，在運行過程中常承受較為復雜的動態載荷，相比于一般機械設備更易發生故障。因此，針對行星齒輪箱的故障診斷研究具有重要意義[1-2]。

3K行星齒輪傳動作為一種基本行星傳動類型，與2K-H行星輪系相比，結構更為緊湊，能提供更大傳動比范圍和更高的承載能力，在航空航天、工業機器人、微型傳動等領域有著廣泛的應用前景[3-4]。目前關于行星齒輪傳動的故障診斷研究主要集中在2K-H行星輪系上，對于3K行星輪系的研究還較少。

關于行星齒輪傳動的故障診斷方法，其中較為常用和成熟的為基于振動傳感器的箱體振動信號分析[5-6]。但由于行星輪隨行星架繞中心軸的公轉，行星齒輪箱中故障激勵點到測量點傳遞路徑時變，振動信號會產生調制現象，給故障診斷帶來困難[7]。此后部分學者，針對箱體振動信號的調制問題，提出利用齒軸扭轉振動信號的故障診斷方法[8-9]。但該方法同樣依賴角度編碼器等機械檢測設備，存在易受外部噪聲干擾和安裝限制較大等缺點。

為克服上述振動信號缺陷，近年來，電機電流信號分析(motor current signature analysis，MCSA) 逐漸被用于齒輪系統故障診斷[10]。如文獻[11]通過監測風力發電機定子電流信號來檢測發電機組傳動系統故障；文獻[12]提出異步電動機電流信號的調制信號雙譜分析方法，實現對齒輪傳動系統的故障監測；文獻[13]通過定子電流信號分析了時變工況下行星齒輪箱故障。MCSA以電機定子電流為切入點，依據電機定子電流的波動反映扭矩的波動，從而對設備進行故障診斷。在實際操作時，使電機定子電源線 (三相中任一相) 通過霍爾電流傳感器或電流鉗，利用霍爾磁平衡原理，將電流信號經采集卡轉化為可以識別的信號，屬于無創檢測，具有容易獲得、抗干擾能力強等特點[14]。但目前關于MCSA的理論分析大多基于數學模型的推導，將轉矩波動設定為具有固定幅值和故障頻率的簡諧形式，并不能反映如時變嚙合剛度和阻尼等齒輪系統內部參數的影響[15-16]。

鑒于此，本文以電驅動3K-II型行星傳動系統為研究對象，綜合考慮齒輪傳動部分時變嚙合剛度、阻尼、齒側間隙、綜合嚙合誤差等非線性因素和電機-減速器系統內部機-電-磁耦合效應，建立了系統的機電耦合動力學模型。并以此為基礎，通過去工頻邊帶頻譜和包絡解調譜對不同齒輪存在裂紋故障時的定子電流信號進行了分析，探討了齒輪裂紋故障對電流信號的調制作用。分析結果表明本文提出的機電耦合模型的合理性，能夠準確模擬電機-3K減速器系統電流信號中的齒輪裂紋故障特征，可為研究各類齒輪故障情況下的電機定子電流信號和相關故障診斷技術提供理論指導。

1 3K型行星傳動系統機電耦合動力學建模

1.1 齒輪系統動力學模型

以3K-II型行星輪系為研究對象，建立如圖1所示，包含電動機 (轉子)及負載的平移-扭轉耦合集中參數模型。其中，下標c,b,e,s,pn,M,L(n=1,2,…,N,N為行星輪個數)分別為行星架、齒圈b、齒圈e、太陽輪、行星輪、電動機(轉子)和負載。下標spn，bpn，epn分別為太陽輪-行星輪、齒圈b-行星輪、齒圈e-行星輪齒輪副。定義j=c，b，e，s，pn，M，L；g=spn，bpn，epn。本文如無特殊說明，均沿用此下標。kjx，kjy分別為各構件沿x方向、y方向的支撐剛度；cjx，cjy分別為各構件沿x方向、y方向的支撐阻尼系數；kju為各構件扭轉支撐剛度；cju為各構件扭轉支撐阻尼系數；kcMu,cLu分別為與電動機(轉子) 和負載相連的聯軸器扭轉剛度；ccMu,cLu為與電動機(轉子) 和負載相連的聯軸器扭轉阻尼系數；kg為各齒輪副時變嚙合剛度，cg為各齒輪副嚙合阻尼系數，eg為各齒輪副綜合嚙合誤差。令齒圈b固定，太陽輪為輸入構件，齒圈e為輸出構件，即電動機輸出轉子與太陽輪連接，外部負載與齒圈e連接。采用牛頓運動定律建立系統運動微分方程如下。

圖1 3K-II型行星輪系平移-扭轉耦合動力學模型Fig.1 Translational-torsional coupling dynamics model of the 3K-II planetary gear system

電機轉子

(1)

太陽輪

(2)

ψsn=π/2+ψn-αs,ψn=2(n-1)π/n,

n=1,2,…,N,

δspn=(xs-xpn)cos(ψsn)+(ys-ypn)sin(ψsn)+

rsbθs-(-rpbθpn)-rcbθccosαs+espn(t)

齒圈b

(3)

ψbn=π/2-(ψn+αb),

δbpn=-(xb-xpn)cos(ψbn)+(yb-ypn)sin(ψbn)+

rbbθb-rpbθpn-rcbθccosαb+ebpn(t)

齒圈e

(4)

ψen=π/2-(ψn-αe)

δepn=(xe-xpn)cos(ψen)-(ye-ypn)sin(ψen)-

rebθe+rpbθpn+rcbθccosαe+eepn(t)

行星架

(5)

行星輪

(6)

負載

(7)

(8)

考慮到動態嚙合過程中，各構件轉速往往圍繞某一值波動，而非保持不變，通過構件轉速來表示時間和誤差項的對應關系不夠恰當。本文使用各構件相對行星架的轉角位移來表示各誤差激勵項。

eg(θ)=Egsin(Z1θ1c+φg)

(9)

式中:Eg為各齒輪副綜合嚙合誤差幅值；Z1和θ1c分別為各齒輪副主動輪的齒數及其相對于行星架轉角；φg為各齒輪副綜合嚙合誤差初始相位。

同理，通過勢能法[17-20]計算的各齒輪副時變嚙合剛度也可表示為隨轉角變化的形式

(10)

(11)

式中：上標i為第i個嚙合齒對；Ntooth為同時參與嚙合的齒對數；下標1，2分別為主、從齒輪；假定主動輪裂紋故障出現在第一個嚙合齒對初始位置，取w=mod(θ1c-2π(i-1)/Z1,Z1θT)，s=mod(w,ceil(ε)θT)；其中θT=2π/Z1為主動輪相對于行星架的嚙合角周期；mod為取余函數；ceil為向上取整函數；ε為齒輪副重合度。

將式(1)～式(7)進行整理，可得系統運動方程的矩陣形式如下

T(t)+F(t)

(12)

式中：M，G，Cb，Cm，Kb，Km，KΩ分別為廣義質量矩陣、陀螺矩陣、支撐阻尼矩陣、嚙合阻尼矩陣、支撐剛度矩陣、嚙合剛度矩陣和向心剛度矩陣；T(t)和F(t)分別為外部激勵力向量和內部激勵力向量；q為位移向量。

1.2 永磁同步電機數學模型

永磁同步電機因其效率高、功率密度高等特點，在現代工業生產中被廣泛應用。本文擬以永磁同步電機驅動的電機-減速器系統為對象建立3K型行星輪系機電耦合動力學模型。

永磁同步電機物理模型示意圖，如圖2所示。包括固定的三相繞組磁軸AM，BM，CM(定子) 和以電角速度ωMr轉動的永磁體S-N(轉子)。當定子繞組中接入三相對稱交流電后，將產生旋轉磁場，帶動磁體轉子同步旋轉，用以實現電機輸出軸機械轉動。

圖2 永磁同步電機的物理模型示意圖Fig.2 Diagram of the physical model of a permanent magnet synchronous motor

為降低模型復雜程度，便于求解，本文采用Park變換，將三相繞組用相互獨立的兩項正交對稱繞組等效替代，在dM，qM坐標系(圖2中淺色磁軸) 中建立永磁同步電機數學模型[21-22]。相應的三相-兩相坐標變換公式、電壓方程、磁鏈方程、電磁扭矩計算公式分別如式(13)～式(16)所示。

(13)

(14)

(15)

TM=1.5pM(ΨMfIqM+(LdM-LqM)IdMIqM)

(16)

1.3 機電耦合動力學模型

圖3 3K型行星傳動系統機電耦合關系示意圖Fig.3 Diagram of electromechanical coupling relationship of 3K planetary transmission system

(17)

式中:第一個方程為3K行星傳動系統機械部分受迫振動模型;第二個方程為電氣系統等效電路模型;U=[VdM,VqM]T為電壓向量;I=[IdM,IqM]T為電流向量;Ψ=[ΨdM,ΨqM]T為定子磁鏈向量;ΨMf=[0,ωMrΨMf]為轉子磁鏈向量。

2 齒輪系統故障對定子電流的影響

2.1 定子電流信號AM-FM數學模型

本節主要從數學公式推導角度討論由故障引起的調制效應對定子電流信號的影響。

假設齒輪故障引起的轉矩波動以故障特征頻率ffault的正弦形式引入，則電機總體負載轉矩可以表示如下

Ts(t)=Ts0+Tsfsin(ωfaultt+φfault)

(18)

式中：Ts0為瞬時平均負載轉矩；Tsf為故障引入轉矩波動幅值；φfault為故障初始相位；ωfault=2πffault為故障角頻率，其中ffault與各齒輪存在裂紋時的故障特征頻率fscf,fpcf,fbcf,fecf對應。

假定電機-減速器系統穩態條件下，電磁轉矩TM=Ts0，則電機轉子轉速可表示為

(19)

式中，ωMr0為電機轉子平均轉速。

對轉子轉速ωMr(t)積分，可得轉子轉角位移

(20)

對于永磁同步電機，在定子坐標系中的轉子磁動勢可表示為

FMr,(Ms)(θMs,t)=FMrsin{pM[θMs-θMr(t)]}=

(21)

式中：FMr為轉子磁動勢幅值；ωps=pMωMr0為供電頻率；pM為磁極對數；θMs為定子坐標系中的轉子角位置。

而定子坐標系中的定子磁動勢與齒輪故障引起的轉矩波動無關[23]，可以寫為

FMs,(Ms)(θMs,t)=FMssin(pMθMs-ωpst)

(22)

式中，FMs為定子磁動勢幅值。

氣隙磁通密度可表示為總體磁動勢和氣隙磁導率之積

B(θMs,t)=Λ[FMs,(Ms)(θMs,t)+FMr,(Ms)(θMs,t)]=

BMssin(pMθMs-ωpst)+

(23)

式中，氣隙磁導率Λ被視為常數。通過對B(θMs,t)關于轉子轉角θMs積分可得定子任意項磁通量

ΨMssin(ωpst)

(24)

式中，BMs, Mr和ΨMs,Mr分別為由定子和轉子造成的氣隙磁通密度和磁通量幅值。

又，對于定子任意相電壓有

V(t)=RMsI(t)+dΨ(t)/dt

(25)

結合式(24)、式(25)，定子電流I(t)可表示為

Is0sin(ωpst)-IMsωpscos(ωpst)-

(26)

式中：Is0為流過定子電阻的電流幅值；IMs=ΨMs/RMs；IMr=ΨMr/RMs。

由上述數學推導過程可知，齒輪故障對定子電流信號同時有調頻和調幅效果，載波頻率為電源供電頻率ωps，調制頻率為齒輪故障特征頻率ωfault。這為通過定子電流信號進行電機-減速器系統故障診斷提供了依據。

2.2 定子電流信號故障特征分析

依據建立的定子電流AF-FM模型，分別從調頻和調幅角度，分析電機-減速器系統齒輪故障在頻譜和包絡譜圖中的表現特征。

2.2.1 頻譜分析

根據雅可比-安格爾恒等式

(27)

可將調頻函數寫成

(28)

式中，Jm(z)為m階第一類Bessel函數。則式(26)中的定子電流可表示為

(29)

對式(29)進行傅里葉變換可得

exp[-jarctan(IMsωps/Is0)]-

δ[ω-ωps]exp[jarctan(IMsωps/Is0)]}-

exp(-jmφfault)+δ[ω-(ωps+mωfault)]·

{δ{ω-[(ωps+(m+1)ωfault)]}exp[j(m+1)φfault]+

δ{ω+[(ωps+(m+1)ωfault)]}exp[-j(m+1)φfault]}-

[(ωps+(m-1)ωfault)]}exp[j(m-1)φfault]+

δ{ω+[(ωps+(m-1)ωfault)]}·

exp[-j(m-1)φfault]}

(30)

式中，δ(·)為單位脈沖函數。

由式(30)可知，定子電流信號將會在頻率±(ωps±mωfault)處，即正負供電頻率±ωps附近，出現邊帶，邊帶間隔為故障頻率ωfault。如考慮供電頻率的高階諧波，邊帶可能會在±(lωps±mωfault)處出現，其中m，l為正整數。

2.2.2 包絡譜分析

根據式(26)中定子電流表達式的第二項可知，其振幅受故障頻率調制作用。對第二項幅值進行傅里葉變換可得包絡譜

δ(ω-ωfault)exp(jφfault)]+IMrωpsδ(ω)

(31)

由式 (31) 可知，在頻率±ωfault處包絡譜會出現峰值。如考慮高階諧波，峰值也會在±mωfault處出現，其中m為正整數。

3 基于3K行星輪系機電耦合模型的定子電流仿真信號分析

3.1 基于機電耦合模型的定子電流信號仿真

本文選定的3K行星傳動機電耦合系統中減速器部分和電機部分主要參數,分別如表1和表2所示。

表1 機電耦合系統減速器部分主要參數Tab.1 Main parameters of the reducer part of the electromechanical coupling system

表2 機電耦合系統電機部分主要參數Tab.2 Main parameters of the motor part of the electromechanical coupling system

考慮到太陽輪與齒圈e在行星輪同齒側嚙合，齒圈b在行星輪另一側嚙合的情況，為模擬局部齒根裂紋故障影響，本文針對5種齒輪裂紋故障情況進行分析，即：①太陽輪齒根裂紋；②太陽輪-齒圈e側行星輪齒根裂紋；③齒圈b側行星輪齒根裂紋；④齒圈b齒根裂紋；⑤齒圈e齒根裂紋。本文主要為探討基于電驅動3K行星傳動機電耦合模型，采用電機定子電流信號進行齒輪裂紋故障定位的可行性。基于這一研究目的，假定各齒輪裂紋均為直線且長度(1.32 mm) 和角度(65°)一致，上述 5種裂紋故障情況下受故障影響的各齒輪副嚙合剛度,如圖4所示。

(a) 太陽輪齒根裂紋

(b) 太陽輪-齒圈e側行星輪齒根裂紋

(c) 齒圈b側行星輪齒根裂紋

(d) 齒圈b齒根裂紋

(e) 齒圈e齒根裂紋圖4 受裂紋故障影響的嚙合剛度曲線Fig.4 Meshing stiffness curves affected by crack faults

(a) 正常情況

(b) 太陽輪故障

(c) s-e側行星輪故障

(d) b側行星輪故障

(e) 齒圈b故障

(f) 齒圈e故障圖5 定子電流信號時域波形Fig.5 Time domain waveforms of stator current signals

表3 各特征頻率Tab.3 Each characteristic frequency Hz

從圖5所示的6種齒輪健康狀況下的定子電流信號時域波形中可以看出，正常情況和各類齒輪裂紋故障情況下的波形區別并不明顯，供電頻率占絕對優勢，表現為簡諧形式。

為提取定子電流信號中的故障特征，本節依據前文所述，分別對信號頻域邊帶和包絡譜進行分析。

3.2 頻域邊帶分析

由圖5可知，定子電流信號主要表現為以供電頻率為主頻率的簡諧形式，直接對電流信號進行傅里葉變換，頻譜主要為供電頻率處的脈沖信號，使得其余特征頻率被淹沒在其中。因此，要分析電流信號頻域邊帶特征需對其進行去工頻處理。本文采用時移疊加的方式來去除工頻，該方法易操作，便于工業應用。

3.2.1 時移疊加

時移疊加即將電流信號與其平移半個周期后的自身相加，以消除基頻信號的方法，根據上文建立的電流信號AM-FM(amplitude modulation-frequency modulation)模型，取式(29)所示電流信號，時延半個周期可得

(32)

(33)

式中，Tps=2π/ωps為供電周期。

由式(32)、式(33)可以看出，時移疊加后的電流信號能有效去除電流中的基頻，而保留由故障引起的調制成分。

3.2.2 去工頻后電流頻譜

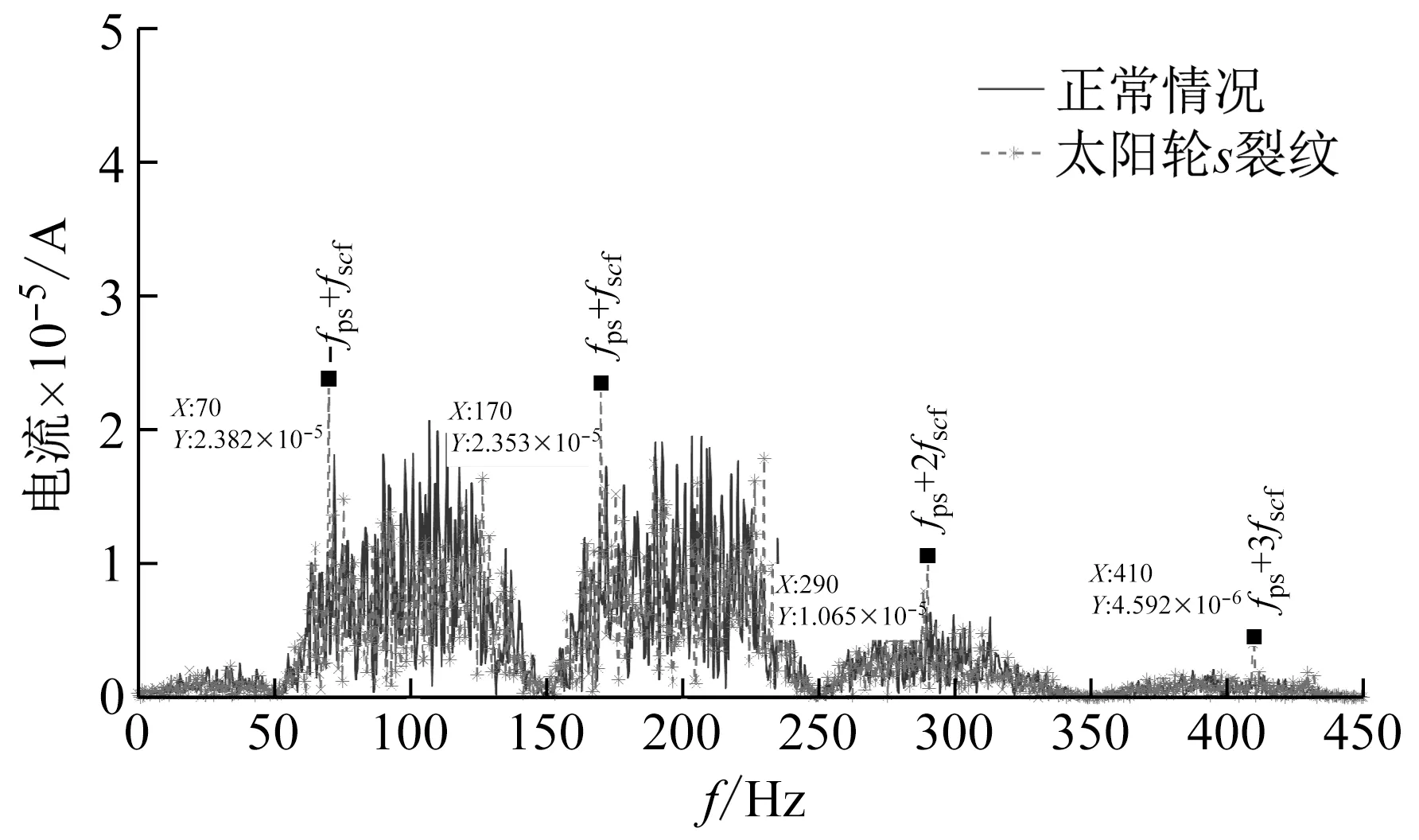
去工頻后的電流殘余信號傅里葉頻譜，如圖6所示。從圖6可以看出，去工頻后的電流傅里葉譜圖中消去了主導的供電頻率 (fps=50 Hz)，而保留了邊帶。當齒輪箱存在故障時，會產生新的邊帶成分，這些邊帶與故障頻率相關。

(a) 太陽輪故障

(b) s-e側行星輪故障

(c) b側行星輪故障

(d) 齒圈b故障

(e) 齒圈e故障圖6 電流信號去除工頻后的傅里葉譜Fig.6 Fourier spectrum of current signal after removing power supply frequency

由圖6(a)可知，新出現的邊帶成分對應正負供電頻率加減太陽輪故障頻率的倍頻，即±fps±mfscf，其中m為正整數，如170 Hz=fps+fscf，70 Hz=-fps+fscf，這與2.2節中關于定子電流信號的頻譜分析結果對應。這種現象意味著太陽輪存在故障。

在圖6(b)和圖6(c)中，新出現的邊帶成分與正負供電頻率加減行星輪故障頻率的倍頻相對應，即±fps±mfpcf，如207 Hz=fps+6fpcf，107 Hz=-fps+6fpcf，這一特征表示行星輪存在故障。

在圖6(d)所示的齒圈b故障對應的頻譜中，在正負供電頻率加減齒圈b故障頻率的倍頻處出現新的邊帶成分，即±fps±mfbcf，如200.5 Hz=fps+5fpcf，70.5 Hz=-fps+4fpcf。

而當齒圈e出現故障時，相應的在正負供電頻率加減齒圈e故障頻率的倍頻，即±fps±mfecf處，出現新的邊帶，如222 Hz=fps+6fecf，93 Hz=-fps+4fecf。

通過對比5種齒輪故障情況可知，由太陽輪故障引起的邊帶成分雖然也能識別，但與其他幾種故障相比不夠明顯。這與3K型行星輪系傳動比較大而導致的輸入端傳遞扭矩較小，且3K-II型的一體式雙聯行星排結構使得齒輪對s-p(n)的有效嚙合齒寬相比于其他齒輪對較大相關。此外，值得注意的是，在各齒輪故障引起的邊帶成分中包括供電頻率fps的負值，這一現象與Chen等研究中的結果存在差別，這可能與故障頻率和供電頻率相近甚至超過供電頻率有關。

3.3 包絡譜分析

通過2.2節中的分析可知，頻譜邊帶中包含故障頻率和供電頻率的組合成分，并不能直觀顯示出故障特征。而包絡譜中峰值與故障特征直接相關，本節通過采用Hilbert變換幅值解調的方式獲得包絡譜。

各齒輪裂紋故障下的包絡譜，如圖7所示。與正常情況相比，在齒輪故障情況下，包絡譜中會出現新的峰值，這些峰值位置與故障頻率對應。

(a) 太陽輪故障

(b) s-e側行星輪故障

(c) b側行星輪故障

(d) 齒圈b故障

(e) 齒圈e故障圖7 電流信號包絡譜Fig.7 Envelope spectrum of current signal

對于太陽輪故障，從圖7(a)中可以看出，在頻率120 Hz處(fscf)包絡譜幅值有所增加，這與太陽輪故障頻率一致。與其他齒輪故障相比，圖7(a)中太陽輪故障特征不夠明顯，這一現象同上文頻率邊帶分析對應。

在圖7(b)和圖7(c)中，可以看出在行星輪故障頻率及其倍頻處相比于正常情況幅值明顯增加，如131 Hz=5fpcf，157 Hz=6fpcf，這表明行星輪存在故障。

當齒圈b存在故障時，可以從圖7(d)中看出在齒圈b故障頻率及其倍頻處出現明顯的峰值，如60.5 Hz=2fbcf，180.5 Hz=6fbcf。這一現象說明了齒圈b存在故障。

而對于齒圈e故障，與正常情況相比，圖7(e)中出現了新的峰值成分，這些峰值位置與齒圈e故障頻率及其倍頻對應(28.5 Hz=fecf，172 Hz=6fecf)。這同樣說明了齒圈e存在故障。

通過上述分析，說明電機定子電流信號能夠準確反映3K行星齒輪箱的故障特征信息，電流信號同時受故障特征的幅值調制和頻率調制作用。也說明了本文提出的機電耦合模型的合理性，能夠準確模擬電機-3K減速器系統電流信號中的齒輪故障特征，為研究各類齒輪故障情況下的電機定子電流信號提供理論指導。

4 結 論

本文通過綜合考慮齒輪傳動部分時變嚙合剛度、齒側間隙、綜合嚙合誤差等非線性因素和電機-減速器系統內部機-電-磁耦合效應，建立了電驅動3K行星傳動系統的機電耦合動力學模型。并基于該模型，計算了5種裂紋故障情況下的時變嚙合剛度，得到了不同齒輪裂紋故障情況下的定子電流仿真信號。通過時移疊加去工頻頻譜和包絡解調譜對電流信號進行分析，得到下列結論：

(1) 定子電流信號受故障特征的頻域調制作用。在通過時移疊加去工頻后的頻譜中，齒輪故障表現為圍繞供電頻率及供電頻率負值的變頻帶，邊帶間隔為故障頻率。且由于3K行星輪系大速比特點，各齒輪故障頻率與供電頻率接近或超過供電頻率，在頻率正軸出現的邊帶成分中包含供電頻率負值。

(2) 定子電流信號受故障特征的幅值調制作用。在包絡解調譜中，齒輪故障表現為在故障頻率及其倍頻處出現峰值。

(3) 由于3K行星輪系傳動比較大，電機輸入端扭矩較小，且3K-II型特殊的一體式雙聯行星排結構令齒輪對s-p(n)的有效嚙合齒寬相比于其他齒輪副較大。太陽輪故障在定子電流頻譜邊帶和包絡譜中雖能識別，但相較于其他齒輪故障，表現不夠明顯。

(4) 通過機電耦合模型得到的電機定子電流信號分析結果與通過AM-FM數學模型分析結果吻合，表明本文提出的機電耦合模型的合理性，能夠準確模擬電機-3K減速器系統電流信號中的齒輪故障特征，為研究各類齒輪故障情況下的電機定子電流信號提供理論指導。