考慮作動器輸出飽合的光電平臺終端滑模神經網絡控制

朱志忠， 袁 鑫， 趙 豐， 董登峰

(1.中國科學院微電子研究所,北京 100049;2.北京航天控制儀器研究所,北京 100854)

在光電偵察、探測識別與跟蹤瞄準領域，為了保證光電載荷在慣性空間視軸指向的穩定性，常常將其安裝于具有陀螺穩定功能的平臺框架上。陀螺穩定平臺能夠有效減小外部各種擾動對光電負載的影響，保證光學負載成像的穩定精度[1]。對于影響視軸穩定精度的干擾因素，主要來源于軸端摩擦力矩、載體振動、環境中的風阻及平臺自身的不平衡力矩等，通過控制方法直驅內、外框架力矩電機進而補償載體姿態的變化，能夠保證光電平臺的整體性能[2]。

光電平臺各個框架由內向外的角速度存在交叉耦合，現有大部分文獻是在陀螺穩定平臺動力學解耦模型的基礎上，從平臺框架動力學特性、擾動力矩分析與建模，干擾觀測與補償等方面展開研究[3-6]。如文獻[7]中陀螺采集的框架角速度和編碼器測量得到的框架角，構建等價捷聯慣性穩定回路。提出基于逆模型前饋的復合控制方法。文獻[8]利用擴張觀測器對慣性穩定平臺的內外總體擾動進行觀測，通過PID(proportion integration differentiation)控制器進行誤差反饋控制，穩定精度顯著得到提升。慣性穩定平臺中系統參數，如負載轉動慣量、傳感器信號誤差與摩擦力矩等均存在一定的參數不確定性。針對這種問題，許多學者提出了高動態跟蹤控制算法，例如滑模控制(sliding mode control, SMC)[9]、模糊控制[10]以及自抗擾控制[11]等。其中，滑模控制對非線性系統具有較好的控制效果，然而，在滑模面上的延遲切換與參數界限的不確定會引起被控框架平臺的高頻抖動[12]。針對這一問題，提出將多種控制器與滑模進行綜合與優化，將反演控制方法與滑模控制相結合[13]，形成響應速度更快、魯棒性能更強及高穩定精度的復雜智能控制算法。文獻[14]設計了基于終端滑模面的有限時域魯棒控制器，該控制律可以確保跟蹤誤差在有限時間內快速收斂至零。神經網絡技術具有在動態系統中逼近非線性函數的優勢，可在沒有準確系統動力學先驗知識下設計基于神經網絡的自適應控制器。文獻[15]提出了一種基于自適應徑向基函數(radial basis function,RBF)神經網絡和擴展狀態觀測器的反饋控制方法，RBF神經網絡可在線生成反饋控制參數。文獻[16]提出神經網絡復合跟蹤控制器，用以估計與補償三軸慣性穩定平臺的系統參數的不確定和外界環境的擾動。

對于機載光電平臺在飛機大俯仰角爬升工況下，框架電機的輸出可能會出現力矩飽和現象，為了滿足負載平臺的穩定性，文獻[17]采用基于有限濾波器與擴展狀態觀測器的改進自適應魯棒控制算法，確保在執行器輸出飽和狀態下光學鏡片的穩定性和跟蹤性能。文獻[18]提出在力矩電機飽和情況下通過線性矩陣不等式最優狀態反饋的方法，實現兩軸慣性穩定平臺外界基座擾動的有效衰減。文獻[19]針對有界虛擬控制律引入線性飽和函數，從而在輸入飽和的情況下確保系統的全局穩定性。

本文建立了包含軸端摩擦力、系統參數不確定的兩軸光電平臺非線性耦合動力學模型，分析了內外擾動對圖像穩定的影響。提出終端滑模結合RBF神經網絡控制器對光電穩定平臺進行跟蹤控制，RBF神經網絡的非線性逼近能力用于克服系統的不確定性和框架之間耦合擾動。同時，設計的輔助函數用以補償理想控制設計和實際輸出扭矩之間的誤差。基于李雅普諾夫穩定性理論，推導與證明了加權矩陣的更新律和閉環系統的穩定性。

1 建模與分析

1.1 慣性穩定平臺動力學建模

引入大地坐標系(xE,yE,zE)、負載相機所在俯仰軸的坐標系(xP,yP,zP)、方位框架所在的坐標系(xA,yA,zA)及與運載器相連的基座坐標系(xB,yB,zB)。如圖1所示。

圖1 各個坐標系之間的旋轉關系Fig.1 Rotation relationship between each coordinate system

根據圖1旋轉關系，基座坐標系至方位框架坐標系變換矩陣RAB、方位框架至俯仰框架的變換矩陣RPA如下所示。

(1)

(2)

定義基座、方位框與俯仰框相對大地坐標系下的轉動角速度分別為ωB=[ωBxωByωBz]T，ωA=[ωAxωAyωAz]T和ωP=[ωPxωPyωPz]T。各個框架角速度之間的角速度關系如下

ωA=RABωB+η

(3)

(4)

根據歐拉方程建立兩軸慣性穩定平臺動力學方程如下所示[20]。

(5)

式中，矩陣HP如式(6)所示

(6)

Exx,Eyy與Ezz為內框架相對內框坐標系x，y和z的轉動慣量，Exy,Exz與Eyz為內框架相對其他軸的慣量矩。俯仰軸電機轉矩TPx可表示為

(7)

式中:TPx為俯仰軸電機的控制轉矩;TPe和TPc為外框架旋轉的耦合項;TPd為俯仰框相對于方位框架的擾動項，分別如下式所示

光電陀螺平臺內框為俯仰框，外框的旋轉需考慮內框的運動，則有

HA=JAωA+RAPHP

(11)

由式(11)可得外框的動力學方程為

(12)

式中:TAz為方位電機的轉矩;TAe和TAc為動態不平衡慣性矩陣的影響;TAd為內部俯仰框相對于方位框旋轉運動的交叉耦合項。

IA=Azz+Ezzsin2θp+Eyycos2θp-Ezysin 2θp

(13)

TAe=(Axx-Ayy-Exx+Ezzcos2θp+

Eyysin2θp+Eyzsin 2θp)ωAxωAzcosθp

(14)

(15)

2Eyz(ωAzsin 2θp+ωAycos 2θp)+

(Exysinθp+Exzcos 2θp)(ωAx+ωPy)-ExxωAzθa]+

ωPxωPy

(16)

1.2 軸端摩擦力建模

為了精確地描述光電平臺的動力學響應，需要建立框架軸端的摩擦力模型。光電平臺常工作在低速旋轉的狀態，擬采用Stribeck摩擦力模型反映軸端靜摩擦與動摩擦連續變化的情況，如下所示[21]。

(17)

式中:Mc為庫倫摩擦力；Ms為最大靜摩擦力；ω為接觸面的相對轉動角速度；σ為黏滯摩擦因數；ωs為Stribeck速度。

2 光電平臺控制系統分析

本文采用終端滑模控制器對光電平臺電機力矩進行控制。選用徑向基神經網絡進行非線性函數的逼近與估計。引入輔助函數補償理想控制器和實際輸出扭矩之間的誤差，使力矩電機避免長時間工作在飽和輸出狀態，以保證穩定平臺具有響應更快、穩定精度高的性能。

定義x1=θPx，x2=ωPx，x3=θPz，x4=ωAz，對式(7)與式(12)進行變換，有

(18)

(19)

式中符號表示如下

(20)

(21)

在式(18)與式(19)中，平臺系統模型參數不確定與外界的擾動綜合表示為

Ξi=ΔFi(t)+ΔBiT+Di(t),i=1,2

(22)

式中,Δ為系統參數的不確定性。控制器實際輸出的轉矩如式(23)所示

(23)

引理：若f(x)為非線性連續函數，存在一個神經網絡表達式WTΘ(x)能夠以任何精度逼近函數f(x)，即

f(x)=WTΘ(x)+ε

(24)

(25)

式中:μ=[μ1,μ2,…,μN]T和ηi分別為高斯函數的中心和寬度;n為x向量的維數;ε(x)為神經網絡的逼近誤差且有界。

3 終端滑模神經網絡控制器設計

跟蹤誤差定義為e=x1-xθ_desired，式中，xθ_desired為理想的參考角度軌跡，對跟蹤誤差e求二次導數，并將式(18)代入有

(26)

式中，Ξ=ΔF(x,t)+ΔBTu+D(t)。

引入終端滑模面設計力矩電機的輸出轉矩Tu，終端滑模面的表達式如下所示。

(27)

式中，β為正實數，且0<φ<1。滑模面s的導數為

(28)

(29)

引入輔助函數進而分析框架電機飽和輸出時的影響，輔助函數如式(30)所示。

(30)

式中:Δτ=Tu-Tc，Kυ∈R+;μ為較小的正實數且ζ∈R為中間輔助設計變量。考慮到滑模面s與狀態變量ζ對光電穩定平臺系統的穩定性的影響，提出李雅普諾夫函數如式(31)所示。

第二，突出教學重點，確保幼兒一日活動的高效性。幼兒園一日活動的內容非常豐富，細節較多，因此，幼兒園應在每一學期設置不同的重點，扎實地展開幼兒的教學活動。在教學過程中要注重理論與實踐之間的結合，通過案例的示范、研究討論、實踐與反思等來提高教學活動的時效性。

(31)

對V1求取一階導數，并將式(29)與式(30)代入得到如下表達式

(32)

(33)

根據Tu=Tc+Δτ，將其代入不等式式(33)有

(34)

利用徑向基神經網絡逼近平臺動力學系統中的未知函數，根據引理1，可得到如下表達式

(35)

考慮電機輸出飽和的影響，提出控制律表達式如下

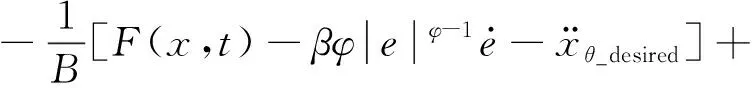
(36)

RBFNN(radial basis function neural network)的權重更新律為

(37)

(38)

(39)

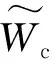
(40)

-(?-0.5)S2-(Kυ-0.5?2-0.5)ζ2+

(41)

將權重與誤差迭代更新律式(37)和式(38)代入式(41)中，可進一步得到

(42)

4 仿真分析與試驗

4.1 仿真分析

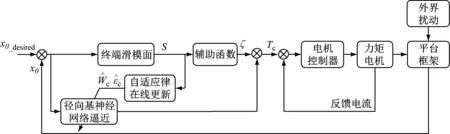
圖2 光電慣性穩定平臺自適應神經網絡滑模控制原理圖Fig.2 Schematic diagram of TSMCNN for inertial stabilization platform

兩框架光電平臺的仿真參數如表1所示。

表1 光電慣性穩定平臺主要參數Tab.1 Main parameters of inertial stabilization platform

在正弦擾動工況下，如圖3所示。從仿真開始時TSMCNN控制力由接近飽和輸出值逐漸振蕩收斂。當達到穩態后，最大跟蹤角度誤差出現在正弦曲線的換向時刻。整個跟蹤過程中，TSMCNN跟蹤角度誤差的(root mean square，RMS)值最小為1.6 mrad，SMC跟蹤角度誤差均方根RMS為3.7 mrad，PID控制方法的跟蹤誤差角RMS最大為25 mrad。

(a) 俯仰軸跟蹤角度曲線

(b) 俯仰框架力矩輸出曲線圖3 基座正弦擾動工況仿真結果Fig.3 Simulation results of sinusoidal disturbance conditions

在受到外界瞬時干擾工況下，如圖4所示，力矩電機的瞬時輸出會接近最大值。從俯仰軸目標角度跟蹤誤差曲線可以看出，TSMCNN在受到瞬時干擾時單邊誤差峰值最小為6.2 mrad，SMC算法跟蹤角度誤差峰值為8.9 mrad，PID角度誤差峰值比TSMCNN惡化了約3.8倍，達到了23.7 mrad。整個過程中TSMCNN算法的跟蹤角度誤差RMS值最小，比SMC算法角度誤差RMS值減小約54%。

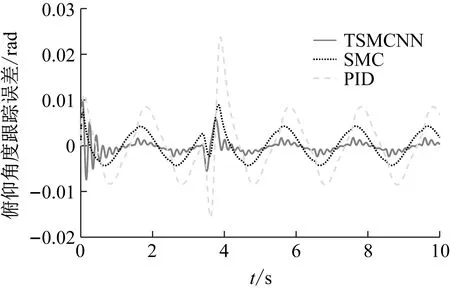
(a) 俯仰軸目標跟蹤角度誤差曲線

(b) 俯仰框架力矩輸出曲線圖4 基座瞬時脈沖干擾工況仿真結果Fig.4 Simulation results of transient pulse interference

4.2 試驗測試

將光電平臺固定于雙軸搖擺測試平臺上。在搖擺臺上位機中載入俯仰軸的運動數據，如圖6所示，進而產生光電平臺的外部隨機擾動角度。

圖5 光電平臺搖擺試驗Fig.5 Photoelectric platform swing test

圖6 雙軸搖擺臺隨機擾動曲線Fig.6 Random disturbance curve of double-axis swing table

通過搖擺臺的搖擺測試，在隨機工況的擾動下，系統穩定后截取4～9 s的俯仰軸陀螺數據，如圖7所示。

圖7 吊艙俯仰軸陀螺輸出曲線Fig.7 Gyro output curve of pod pitch axis

采樣頻率為100 Hz，經過數據處理，TSMCNN算法的減振效果陀螺RMS值為4.7 mrad/s，相對于SMC穩定控制的RMS值減小了8%，而對于傳統的PID算法減小了13.3%。說明了本文提出的算法能夠有效提升光電穩定平臺的性能。

5 結 論

本文建立了雙軸慣性穩定平臺非線性動力學耦合模型，針對光電平臺中存在的系統參數不確定、軸端摩擦力與外界基座擾動等因素，利用徑向基神經網絡估計與補償平臺動力學系統中的未知函數與外界擾動，提出基于RBF神經網絡的終端滑模控制器對框架平臺伺服系統進行控制。考慮無刷直流力矩電機在實際應用中的輸出飽和特性，引入輔助函數用以補償理想控制力矩和實際輸出力矩之間的誤差，提高了光電負載圖像的穩定性與動態目標跟蹤的快速性。從理論上應用李雅普諾夫方法證明了伺服控制系統的漸進穩定性，通過仿真與試驗分析表明，本文提出的算法具有較小的目標跟蹤誤差與較強的魯棒性，TSMCNN算法的減振效果陀螺RMS值為4.7 mrad/s，相比于傳統的PID控制提高了13.3%。