基于經驗小波變換-噪聲輔助分析的橋梁信號降噪方法

羅燁鈳， 陳永高， 李升才

(1.浙江工業職業技術學院 建筑工程學院，浙江 紹興 312000； 2.華僑大學 土木工程學院，福建 泉州 362000)

橋梁健康監測系統通過監測結構關鍵部位的荷載與環境、結構響應以實現結構狀態的評估，從而輔助橋梁運維、確保交通運輸安全運行。實際工程中的橋梁運營環境極為復雜，監測系統往往會受到噪聲干擾，使得能夠反映結構特征信息的監測信號淹沒于噪聲中，給橋梁結構狀態評估帶來極大影響。因此，在實橋監測信號分析前需通過合理的方法對采集信號開展降噪處理，最大程度地降低噪聲干擾，為橋梁結構狀態評估提供合理可靠的數據基礎。

目前，橋梁信號降噪中應用較多的方法有經驗模態分解(empirical mode decomposition，EMD)、小波變換(wavelet transform，WT)和奇異值分解(singular value decomposition，SVD)。EMD和WT通過對信號進行分解、篩選、重構實現降噪，SVD通過選定合適的奇異值階次進行信號重構實現降噪。路華麗[1]基于EMD濾波及切比雪夫濾波對某單塔自錨式懸索橋變形監測數據進行了有效降噪；顏潮勇[2]基于WT提出了分層、分段降噪方法，并通過蘇通長江公路大橋GPS(global positioning system)監測數據進行了驗證；熊春寶等[3]將完備集合經驗模態分解(complete ensemble empirical mode decomposition，CEEMDAN)與WT結合，對某大跨度斜拉橋主梁豎向位移數據進行了降噪；董林鷺等[4]提出了一種基于局部均值分解和 SVD 的降噪方法，通過 SVD 對局部均值分解法分解篩選后的分量信號進行降噪，實現了對微震信號中高頻噪聲的去除；葉錫鈞[5]提出了基于GA-SVD(genetic algorithm and singular value decomposition)的自適應降噪算法，并以某斜拉橋和某連續梁拱橋的振動信號為研究對象進行了驗證。

橋梁結構體型質量巨大、運營環境復雜，其監測信號具有信噪比小及細節成份豐富的特點。在橋梁振動監測信號的降噪中，EMD易產生模態混疊，端點效應嚴重，且需要依托外部濾波算法實現降噪，WT需要考慮橋梁結構特征對信號的影響來選擇小波基及閾值函數，SVD的奇異值階次確定大多依賴人工判別，3種方法體系均具有一定的局限性。

經驗小波變換(empirical wavelet transform，EWT)是由法國學者Gilles于2013年提出的一種新的時頻域信號分析方法[6]。EWT能夠通過頻譜分割算法實現頻帶劃分，并基于Meyer小波基構造正交小波濾波器組，擁有完備理論基礎同時兼備較高的計算效率，在機械故障診斷領域得到了成熟應用[7]。相比EMD,WT,SVD等算法，EWT可通過頻譜分割算法實現頻帶精確劃分，并基于Meyer小波基進行本征模態函數(intrinsic mode function，IMF)濾波，針對橋梁振動監測信號具有較好的適應度。本文將EWT引入橋梁監測信號降噪中，并結合工程實際應用需求，提出一種基于噪聲輔助分析理論的橋梁結構響應自適應降噪方法，以實現對復雜環境激勵下橋梁監測信號的降噪。先通過仿真信號對所提方法應用效果進行測試，后以某斜拉橋加速度監測信號為例，驗證了所提方法在實橋監測信號降噪分析中的有效性。

1 EWT原理及降噪分析

1.1 EWT算法

EWT步驟如下。

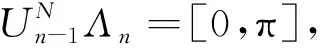
圖1 EWT頻譜分割示意圖Fig.1 EWT spectrum segmentation diagram

步驟2基于頻帶邊界坐標構造濾波器組。根據Little wood-Paley理論構建小波的方法，EWT中Meyer小波基的尺度函數φn(t)及小波函數Ψn(t)在頻域內表達詳見式(1)及式(2)。

(1)

(2)

τn=γωn

(3)

(4)

β(ω)為滿足式(5)的任意函數

(5)

步驟3通過小波基函數濾波得到分量信號。根據WT的方法將EWT的細節系數和近似系數分別定為式(6)和式(7)。細節系數和近似系數分別代表了信號的高頻成分和低頻成分。

(6)

(7)

通過分解所得信號分量為

(8)

(9)

(10)

1.2 EWT降噪分析

隨著EWT的進一步應用，已有諸多學者嘗試將EWT用于機械領域的信號降噪中[8]。EWT實現降噪主要有3類途徑：① 提升頻譜分割精度，使不同頻率成分的特征分量彼此之間得到分離，避免模態混疊，同時使噪聲分量與特征分量分離，避免經Meyer小波基濾波所得IMF分量被噪聲污染[9]；② 提高特征IMF分量的識別精度，通過構造對特征或噪聲分量具有一定敏感度的篩分指標，進而判定IMF中的噪聲分量或無效分量，對其篩分后重構達到降噪目的[10]；③ 對IMF分量進行濾波，如基于WT等方法對IMF分量濾波重構實現降噪[11]。

根據工程應用需求不同，現有基于EWT的降噪案例大多基于上述3類途徑進行組合，但受制于EWT算法的特點，上述3種途徑均具有一定短板。如：途徑①的效果極度依賴頻譜分割方法的分割精度，若頻譜分割不當，會嚴重影響后續的濾波質量，目前大多在頻譜分割前對信號進行譜分析或構造擬合曲線，進而突出信號中的特征譜峰、抑制噪聲譜峰，之后對已平滑的頻譜曲線進行“偽”頻譜分割，得到的頻帶坐標又返至原始信號進行“真”頻譜分割，而此種方法取決于平鋪曲線的平滑效果，不同工程場景中無法統一適用；途徑②的指標建立在人為選擇的基礎上，與EWT中固定的頻譜分割算法不同，指標選擇很大程度依賴研究人員的專業判斷能力，不同的指標對信號的敏感程度不一，如何基于信號特征進行自適應指標構建尚無定論；途徑③將EWT濾波效果依賴于其他算法，構建基于EWT和所選算法的組合降噪框架，該方法雖能夠提升最終的降噪效果，但增加了需要調整的參數，在提高應用難度的同時也降低了算法的自適應性。

2 改進EWT降噪算法

2.1 染噪信號的構造

為抑制EMD分解時的模態混疊和端點效應、降低信號噪聲對分解過程的干擾，Huang基于噪聲輔助分析理論(noise-assisted data analysis，NADA)對EMD進行了改進。NADA理論主要體現為：向原始信號添加高斯白噪聲，基于EMD獲得每次加噪后分解所得IMF分量，再對各組IMF分量集成平均，進而抑制IMF分量中噪聲的影響，重構后即可實現原始信號降噪。

根據Huang所提噪聲輔助分析的思想，向原始信號x(t)中添加標準差比例為σ的高斯白噪聲，根據文獻[12]及EWT算法特點，將σ擬為0.2，將集成次數考慮為迭代次數Ne擬為100。當σ和Nei(i=1,2,…,100)確定時，構造染噪信號為

Xi(t)=X(t)+noise·σ

(11)

式中：noise為高斯白噪聲;Xi(t)為σ下第Nei次集成所得染噪信號。

2.2 有效頻帶的選取

實橋測試信號在環境激勵下的傅里葉譜往往會被噪聲“波浪”影響，這種影響體現在整個頻域內。隨著激勵信息的復雜化及劇烈化，“波浪”會越來越高，直至“淹沒”代表結構特征的幅值。在頻域內，噪聲分布較為均勻且隨機，代表結構固有信息的特征分量分布則較為穩定，且在大多工程案例中，特征分量的頻域幅值往往比噪聲分量高很多。

根據特征分量能量高且穩定、噪聲能量低且隨機的分布規律，本節提出一種基于能量準則的頻帶劃分方法。首先，基于EWT中的Scalespace-Otsu方法對Xi(t)頻帶進行劃分，得到頻帶坐標集合W={w1,w2,…,wj}(j∈N+)，根據Gilles所定規則，將該W標準化于[0,π]內，即w1=0,wj=π。然后，提取j-1個頻帶內的主峰幅值，得到主峰幅值集合A={a1,a2,…,aj}，此處為避免求取頻帶能量時受到大幅值噪聲影響，故以主峰幅值為判斷依據。提取最大主峰幅值的頻帶區間[wm,wm+1](1≤m≤j-1)，利用Meyer小波濾波器組濾波得到FIM,m。定義1階染噪信號為

(12)

按照以上分析流程，在對大多數特征分量所在區間進行定位并濾波得到IMF分量后，殘量頻譜形態主要由兩類構成，即低幅值含噪特征分量與噪聲。針對低幅值含噪特征分量，將以誤差指標進行判斷；針對噪聲分量，理論上當頻域范圍內沒有明顯的高幅值譜峰時，證明特征分量已近似提取完畢，此時無需再進行EWT濾波。然而，噪聲的幅值特征是低且隨機的，當頻域范圍內皆為噪聲分量時，頻譜會呈現出整體幅值較低、所有極大值點的幅值較為接近的多峰形態，本文將其定義為“偽染噪信號”。

2.3 分解終止閾值分析

針對“偽染噪信號”的判斷標準，本節提出一種基于概率密度函數(probability density function，PDF)曲線的自適應判定方法。原始含噪信號傅里葉譜中，含噪特征信號對應的高幅值區域占比較少，噪聲信號對應的低幅值“波浪”區域占比較多，通過對比可知，兩者的分布規律具有較大的差異性，對兩者頻數直方圖的PDF曲線進行峰值位置估計，若峰值位置達到某臨界狀態，則可判定當前信號屬于完全噪聲信號。以某含有4個特征分量及1個噪聲信號的含噪信號為例，X1為原始含噪信號，X2～X5分別為從中去除1～4個特征分量的余量信號。X1～X5的傅里葉譜及對應的PDF曲線如圖2所示。

圖2 X1～X5的頻域統計規律Fig.2 Frequency domain statistics of X1～X5

由圖2可知，隨著信號特征頻點減少，其PDF曲線峰值將逐漸右移，當信號不含特征頻點時，PDF曲線的峰值位置將會穩定于某范圍(見圖2(b)X5)。經過大量試驗，確定該范圍中心穩定于全局分布區間的33%左右，即以33%為臨界閾值。

針對EWT的算法特點，當傅里葉譜某一頻帶經Meyer小波基濾波后，其殘量的傅里葉譜中該區間的幅值曲線將趨近于0，同時呈現出平滑特征，這種與噪聲規律不同的分布形式會使PDF曲線估計產生偏差，因此制定規則如下：

(1) 在單次迭代過程中，第2次及后續分割前需將之前分割得到的能量最大的頻帶剔除，剔除后方可進行PDF曲線估計。

(2) 在單次迭代過程中，當某次分割得到的能量最大區間[wn,wn+1]的頻帶邊界之一wn+1在上一步驟的能量最大區間[wm,wm+1]內時，將wn+1替換為wm。

2.4 IMF分量集成

假設經過p次循環分解后PDF曲線到達臨界閾值，此時可得到p個頻帶區間及p個IMF分量，通過p個頻帶區間又可得p個主峰幅值和2p個頻帶邊界坐標，同時基于隨機減量法又可得p個IMF分量的頻率值。基于噪聲輔助分析思想，對各IMF分量設定集成規則：首先，將各IMF分量按照識別的頻率大小從低頻到高頻排序；其次，為避免集成過程中不同頻段IMF的混疊，定義集成系數Th為

Th=

(13)

第2次迭代結束后可對兩組IMF分量進行第1次集成，小于Th的兩個IMF分量疊加后取平均，對應的兩組特征信息(w,f,a)經同樣平均處理后作為新IMF分量的特征信息，大于Th的兩個IMF分量及對應的特征信息則予以保留，第1、第2次的集成結果將與第3次迭代結果進行第2次集成，后續迭代以此類推。

2.5 有效IMF分量篩分

由于本方法在集成過程中會保留大于集成閾值Th的IMF分量，故當100次迭代結束后，必然會存在幾乎沒有被集成平均或平均次數極少的IMF分量。基于噪聲輔助分析理論可知，該部分IMF分量中仍存在較強的噪聲影響，故應篩分后剔除。針對有效IMF分量的篩分，本節提出一種篩分系數，將能量密度與平均周期乘積ET和JS(Jensen-Shannon)散度結合，通過信號自身噪聲特性及與原始信號間的相關性來進行判別。

Wu等[13]基于能量密度與平均周期的乘積ET對噪聲IMF分量進行了有效判定。兩者定義見式(14)和式(15)

(14)

(15)

式中：E為能量密度;T為平均周期;N為IMF分量的數據長度;Nzc為IMF的過零點個數。當IMF分量特性越接近特征響應，ET值就越大，反之越接近噪聲信號則ET值越小。

JS散度是在KL(Kullback-Leibler)散度基礎上改進的一種衡量相似性的指標，能夠避免KL散度在對兩種不同的分布計算時產生的不對稱性，可較為合理地反映兩種分布的相似程度[14]。以分布P和分布Q為例，兩者JS散度的定義見式(16)

(16)

式中,KL(·)為KL散度。JS散度越大，即證明P和Q的分布越接近，在信號分析中，若某IMF分量與原始信號的JS散度越大，即代表該信號蘊含的特征信息較多，反之則越少。

由于ET指標和JS散度具有不同的分布特征，故通過標準化方法對兩者處理后進行線性平均，形成篩分系數Ts。經過大量試驗發現，當Ts>0.7時，可判定該IMF分量為特征分量，反之則予以篩除。對最終集成所得各IMF分量篩分后再進行特征信號的重構，即可得到最終的降噪信號。本文所提的基于噪聲輔助分析的改進EWT方法降噪具體流程,如圖3所示。

圖3 改進EWT方法降噪流程圖Fig.3 Process of improved EWT noise reduction

3 仿真信號試驗

3.1 降噪評價指標

為對改進EWT方法的降噪效果進行定量分析，引入信噪比(signal-noise ratio，SNR)、均方根誤差(root mean square error，RMSE)、噪聲抑制率(noise suppression ration，NSR)等3個指標，其定義如下

(17)

(18)

(19)

式中：s(i)為初始純凈信號;f′(i)為染噪信號;f(i)為對染噪信號降噪后的信號;N為采樣點數。SNR和NSR隨降噪效果的提升而增大，RMSE反之。

3.2 仿真信號構造

構造正弦信號x1及x4、余弦信號x2、調幅調頻信號x3、自由衰減信號x5，并添加模擬高斯環境噪聲的噪聲信號noise構成含噪仿真合成信號，見式(20)

(20)

將采樣頻率擬為10 Hz，采樣時長2 min，為體現各信號細節，選擇0～30 s的時域波形進行展示，如圖4所示。合成信號加噪前后傅里葉譜如圖5和圖6所示。

(a)

(b)

(c)

(d)

(e)

(f)圖4 信號構成圖Fig.4 Signal composition diagram

(a) 時程曲線

(b) 傅里葉譜圖5 純凈模擬信號Fig.5 Pure simulation signal

(a) 時程曲線

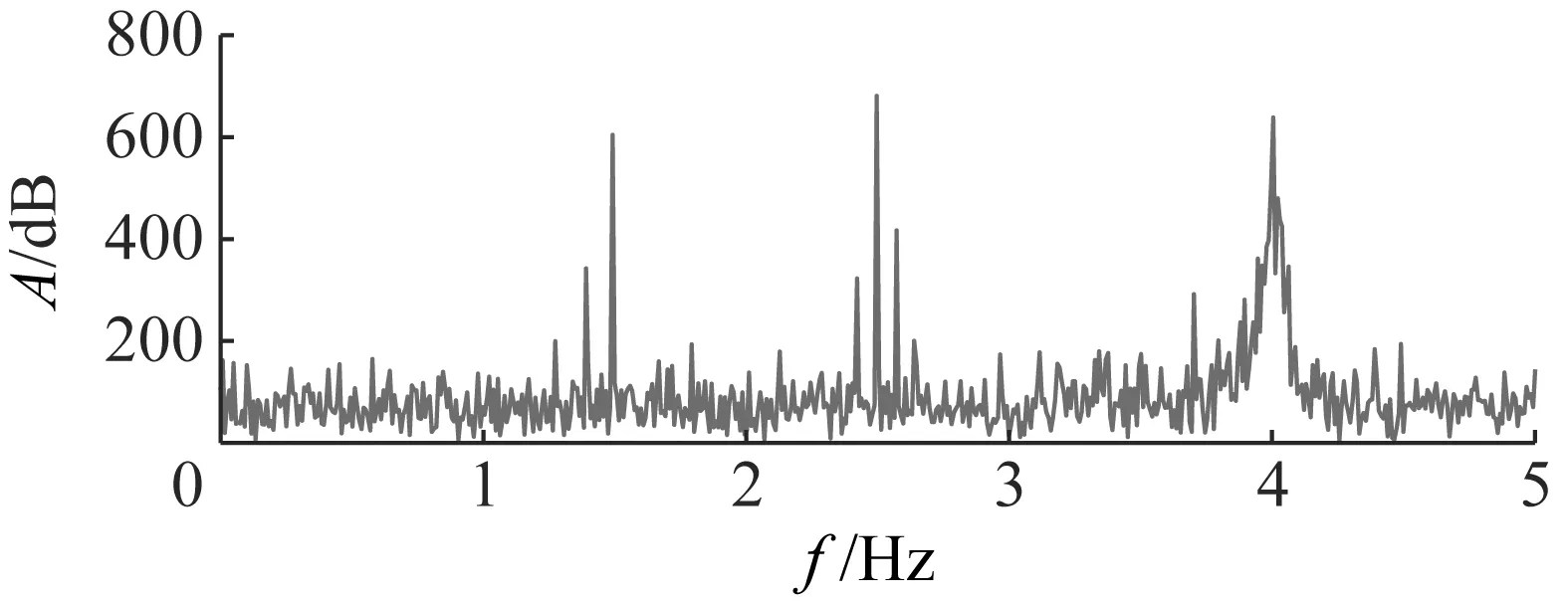
(b) 傅里葉譜圖6 加噪后模擬信號Fig.6 Simulation signal after adding noise

3.3 改進EWT分析及評價

當迭代次數i=1時，染噪信號經改進EWT方法的分析流程如圖7和圖8所示，循環編碼為Ci(i=1，…，N)。6次循環過程對應的峰值位置比例,如表1所示。

表1 前兩組IMF分量的集成系數Tab.1 Integration coefficients of the first two IMF

(a) C1-分割結果

(b) C2-分割結果

(c) C3-分割結果

(d) C4-分割結果

(e) C5-分割結果

(f) C6-分割結果圖7 染噪信號首次迭代分割規律Fig.7 The first iterative segmentation rule

(a) C1-PDF曲線估計

(b) C2-PDF曲線估計

(c) C3-PDF曲線估計

(d) C4-PDF曲線估計

(e) C5-PDF曲線估計

(f) C6-PDF曲線估計圖8 殘量概率密度曲線Fig.8 Probability density curves of residual

當循環次數C為6時，此時PDF曲線峰值位置比例為0.363，超出了33%的閾值限界，故以前5次循環所得IMF分量為有效IMF分量。此外，C3的位置比例較C1,C2偏小，PDF曲線的峰值位置比例從C4開始恢復正常規律，究其原因，可能是C2中的[b8,b9]頻帶受噪聲影響較大，故在濾除該區間后傅里葉譜的整體信噪比有所增強，故對應的峰值位置比例變小。針對實際工程而言，當循環次數達到一定程度時，殘量頻域形態必然會達到接近于噪聲的臨界狀態，基于EWT算法自身特性，無論頻帶受到噪聲的影響強弱與否，改進EWT方法均能夠做出準確的臨界狀態判定。

第1次迭代共得到5階IMF分量，按同樣步驟完成第2次迭代，根據集成規則對兩次迭代過程所得IMF分量進行集成平均，兩組IMF分量對應的集成系數如表2所示。由表2可知，第1次迭代所得5階IMF分量可分別與第2次迭代的IMF21，IMF22，IMF23，IMF25，IMF26等分量進行集成，兩組數據之間的集成系數均大于0.8，滿足集成條件。

表2 前兩組IMF分量的集成系數Tab.2 Integration coefficient of the first two IMF

按相同流程迭代至第100次，此時共得到12個IMF分量，按照2.5節所述流程，計算各IMF分量的能量密度與平均周期乘積ET以及JS散度，對兩者進行標準化后再通過線性平均形成篩分系數，如表3所示。對滿足篩分條件的各IMF分量重構得到降噪信號。

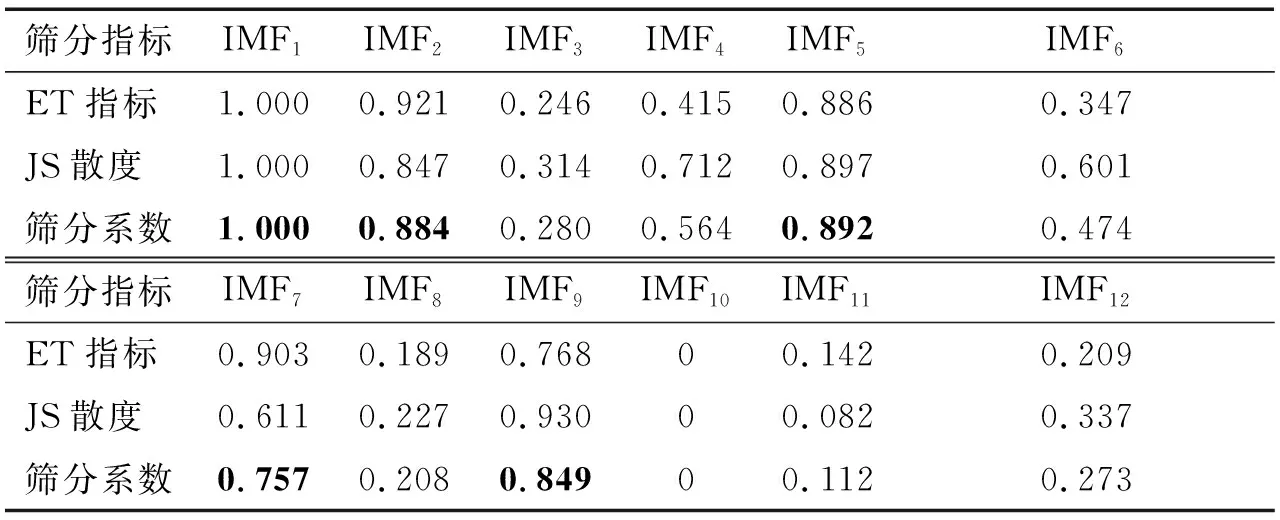
表3 最終迭代所得各IMF分量篩分指標Tab.3 Screening indexes of IMF obtained by final iteration

為量化本文所提改進EWT方法的降噪效果，同時對比該方法的應用性能，分別采用熊春寶等研究中的CEEMDAN-WT降噪、董林鷺等研究中的SVD降噪、改進EWT降噪3種方法對模擬含噪信號進行降噪。其中：CEEMDAN-WT按熊春寶等的研究確定IMF篩分閾值為0.5，選用db6小波基、軟閾值；SVD按董林鷺等的研究采用加權能量貢獻率確定奇異值有效階數，閾值為0.1%。

CEEMDAN-WT和改進EWT分解所得IMF分量，如圖9所示。由圖9可知，改進EWT的IMF分量要比前者更少，且各分量形式與原始分量信號接近，表明經過改進EWT處理后各特征IMF分量可有效保留并分離，且具有較好的分解精度，CEEMDAN-WT中IMF1～IMF4與原始分量雖較為接近，但未能有效反映原始分量的周期規律，且在分析過程中易混入無效IMF分量。對各方法重構后信號進行對比，時程圖、重構誤差、傅里葉譜，如圖10～圖12所示。由圖10及圖11可知，SVD與改進EWT的重構信號與純凈合成信號相近，CEEMDAN-WT效果則相對較差，且前兩者的重構誤差均比后者要低，改進EWT的最大重構誤差為1.358‰，相比SVD的最大重構誤差4.026‰更低。觀察圖12可知，CEEMDAN-WT重構信號傅里葉譜與原始含噪信號傅里葉譜接近，其中高頻部分降噪效果較低頻部分更明顯，但傅里葉譜全局降噪效果較差。SVD與改進EWT的降噪效果更好，其中，SVD在降噪過程中過濾了x1特征頻率，x3雖然能觀察到頻率主峰，但其調幅調頻特性并未在重構信號傅里葉譜中體現。改進EWT相比SVD降噪效果更好，x3的調幅調頻特征得到保留，在降噪過程中x4受到x5影響較小，未出現SVD降噪后出現的x4特征頻率幅值減小的情況。經綜合分析，改進EWT的全局降噪效果相比CEEMDAN-WT及SVD更好，且相比后兩者能夠更加完整地保留分量信號的頻域特征。

圖9 模擬信號各方法分解結果Fig.9 Decomposition results of simulation signals

(a) CEEMDAN-WT

(c) 改進EWT圖10 重構后的模擬信號Fig.10 Reconstructed simulation signal

(a) CEEMDAN-WT

(b) SVD

(c) 改進EWT圖11 模擬信號重構誤差對比Fig.11 Simulation signal reconstruction error comparison

(a) CEEMDAN-WT

(b) SVD

(c) 改進EWT圖12 重構后模擬信號傅里葉譜Fig.12 Fourier spectrum of reconstructed simulation signal

計算重構信號的降噪指標，如表4所示。經前述可知，SNR與NSR越大、RMSE越小，表明降噪效果越好。由表4可知，經改進EWT降噪后重構信號的SNR，NSR，RMSE分別為25.254 dB,1.653×10-3,0.874。觀察可得，SVD的三項降噪指標與改進EWT在數量級保持一致，但仍有一定差距，如SVD的RMSE為4.847×10-3，接近改進EWT對應指標的3倍，而SNR與NSR則較為接近。CEEMDAN-WT的降噪效果最差，其SNR為9.254 dB，是3種方法中的最小值，接近SVD的1/2、改進EWT的1/3，對應的NSR保持同樣的數值規律。此外，由于CEEMDAN-WT未能對信號中的高頻噪聲分量進行有效降噪，導致其RMSE值達到2.986。

表4 重構信號降噪指標Tab.4 Noise reduction index of reconstructed signal

經綜合對比，改進EWT相比CEEMDAN-WT、SVD具有更好的降噪效果，該方法能夠在有效提取特征分量的同時保持較低重構誤差。

4 工程驗證

為驗證改進EWT方法在實橋監測數據分析中具有良好的降噪效果，選用某斜拉橋為研究對象，基于Hilbert-Huang譜對降噪效果進行評價。

4.1 工程概況

該斜拉橋主橋由464 m中跨和兩側對稱布置的216.5 m邊跨組成，主橋全長897 m，屬雙塔雙索面半漂浮體系。大橋跨度大、高程相對較高、車流量多，風荷載和車輛荷載導致橋面振感明顯，該橋加速度傳感器布置形式，如圖13所示。

圖13 加速度傳感器布置圖(m)Fig.13 Acceleration sensor layout (m)

本文選取該橋中跨跨中截面的Z-6#豎向加速度信號為研究對象，采集所用傳感器為941B豎向拾振器，采樣頻率為50 Hz，Z-6#加速度時程曲線及傅里葉譜詳，如圖14所示。由圖14可知，跨中截面特征頻率主要集中在[5,15]Hz，但受環境噪聲影響，特征頻率區間被噪聲淹沒，出現毛刺現象，無法辨別各特征頻率信息。

(a) 時程圖

(b) 傅里葉譜圖14 Z-6#監測數據Fig.14 Z-6# monitoring data

4.2 降噪效果驗證

分別采用CEEMDAN-WT、SVD、改進EWT方法對Z-6#測點的采集信號進行降噪，CEEMDAN-WT與改進EWT方法分解所得IMF分量，如圖15所示;對應的時頻曲線,如圖16所示;3種降噪方法重構信號的傅里葉譜，如圖17所示。

圖15 實橋信號各方法分解結果Fig.15 Decomposition results of bridge signals

圖16 改進EWT分解后的 Hilbert-Huang 譜Fig.16 Hilbert-Huang spectrum of Bridge signal

(a) CEEMDAN-WT

(b) SVD

(c) 改進EWT 圖17 降噪后傅里葉譜Fig.17 Fourier spectrum after noise reduction

由圖15可知，在時域內，CEEMDAN-WT分解得到8個IMF分量，經分析可知IMF1～IMF4為高于15 Hz高頻分量，IMF5,IMF6代表了[5,15]Hz的特征分量，IMF7,IMF8為接近5Hz的低頻分量，改進EWT分解得到6個IMF分量，經分析得IMF1～IMF6均處于[5,15]Hz。在分解數量上改進EWT更具優勢，且通過與原始信號的傅里葉譜對比，CEEMDAN-WT僅有IMF5,IMF6為有效信號分量，而改進EWT的各IMF分量均處于特征頻帶區間，表明改進EWT能夠準確定位信號特征分量所處頻帶范圍。由圖15可知，在時頻域內，改進EWT所得IMF分量的時頻曲線更加清晰和連續，反映出改進EWT方法具備良好的降噪性能。通過圖16中各時頻曲線對應的頻率區間可知，改進EWT的IMF分量特征頻率主要集中在[5,15]Hz，與圖1中原始信號傅里葉譜基本規律一致，即經過頻帶提取、集成平均、分量篩選后，改進EWT能夠在保持分解數量的優勢的同時保留信號特征信息。由圖17可知，在頻域內，SVD與改進EWT均能夠有效抑制環境噪聲對信號中特征分量的影響，在保留特征分量頻率信息的同時能夠避免無效噪聲對特征頻帶的毛刺干擾，CEEMDAN-WT的降噪能力則相對較差。通過觀察可知，改進EWT對6.3 Hz主頻附近的噪聲進行了剔除，而SVD在該位置未能有效降噪，在整體范圍內改進EWT比SVD具備更好的降噪效果。

5 結 論

基于現有降噪算法的局限性，將噪聲輔助分析理論與EWT方法結合，改進了EWT分析過程中存在的有效頻帶選取問題、頻帶數量無法自適應確定、降噪效果較差等問題，通過某斜拉橋監測的動力響應數據，驗證了本文所提方法的有效性，得到以下結論：

(1) 改進EWT方法相比CEEMDAN-WT,SVD具有更強的降噪能力，基于噪聲輔助理論能夠有效抑制噪聲的影響，使最終集成IMF分量的特征信息更為穩定、顯著和豐富。

(2) 基于傅里葉譜的能量準則和PDF曲線峰值位置比例閾值能夠解決頻帶選擇問題，所設參數均基于信號通用特征考量，在實際應用中具備較好的自適應性與推廣性。

(3) 實橋動力響應信號經改進EWT方法處理后，分解所得IMF分量的時頻曲線更加穩定，重構信號的傅里葉譜中被噪聲淹沒的現象減少，表明該方法能夠應用于運營狀態下的橋梁信號分析。