一種高固有頻率的三向隔振系統(tǒng)動力學特性研究

黃子祥， 謝溪凌， 張志誼

(1.季華實驗室，廣東 佛山 528200； 2.上海交通大學 機械系統(tǒng)與振動國家重點實驗室，上海 200240)

隔振設計是保障高性能機載設備輸出精準、穩(wěn)定可靠的關鍵環(huán)節(jié)，當前的機載設備工作環(huán)境存在著如下特點：一方面飛行器的高機動特點易造成振源激勵的寬頻帶和多方向性；另一方面，隨著機載設備的高度集成化、小型化，對隔振系統(tǒng)外形尺寸和質量的限制變得更加嚴格[1-3]。研究匹配于機載環(huán)境的系統(tǒng)隔振方案，對充分發(fā)揮機載設備工作性能、減少環(huán)境因素制約具有較為重要的意義。

從隔振器設計的角度，為獲得較寬的隔振頻帶，希望固有頻率越低越好，但往往受到設備安裝空間的約束和側向穩(wěn)定性的限制，過小的固有頻率易造成承載能力的不足，使系統(tǒng)變形行程無法約束在規(guī)定范圍之內[4]。一些具備“高靜低動”特點的非線性隔振機構從理論上能夠解決承載能力和低頻隔振的矛盾，通過正負剛度并聯的方式，可將靜平衡位置處的微幅振動頻率控制在較低的量值以內[5]。但由于非線性負剛度元件的引入，這類零剛度隔振器普遍存在結構復雜、負載安裝困難、靜平衡位置不穩(wěn)定等缺點[6]，在有限安裝空間的制約下，難以繼續(xù)拓展應用到多個方向的隔振。為滿足結構簡單可靠、小型輕量的要求，本文采用增大隔振器剛度的方式提升承載能力。但剛度的增大會造成隔振頻帶縮短、高頻隔振效果不佳等問題，為此，采用三參數隔振的方式提升系統(tǒng)階數，使高頻段隔振效果滿足使用要求。目前的三參數隔振器多采用可變形金屬容器及流體阻尼結構進行設計[7-8]，但固有頻率鮮有設計到100 Hz以上，且需要考慮在高頻處，如何提供足夠的損耗因子來抑制共振幅值。

在隔振系統(tǒng)設計方面，需要考慮2個問題：一是由于平臺的剛度矩陣存在非對角項，造成單一方向激勵引起多個方向的振動響應，如水平激勵同時引起負載水平和搖擺2個方向的振動，而搖擺造成的測量角偏移是影響精度的最不利因素之一，因此設計低耦合隔振系統(tǒng)十分必要；二是為進一步減小共振發(fā)生的機率，一些場合下要求各自由度上的共振頻率盡可能相等，即隔振系統(tǒng)三向等剛度[9-10]。以多桿并聯為特征的多自由度平臺在載荷隔離方面的應用十分廣泛，如王超新[11]采用一種立方體Stewart平臺，用于抑制有效載荷的在軌微振動，這種平臺的任意相鄰支腿具有正交性，在載荷質心與平臺中心重合的前提下，沿3個線性軸方向的振動可完全解耦，但各尺寸參數需滿足特定的幾何關系，并且還要考慮實現三向平動剛度相等，這對于平臺安裝空間大小提出了很高的要求[12-13]。而在空間局限的場合下，采用非正交Stewart平臺非線性明顯，又不可避免地存在振動耦合。因此，如何運用簡單的布局方式，設計低耦合、三向剛度相等的緊湊型隔振系統(tǒng)，需要進一步的研究。

本文提出一種基于三參數隔振器組件的隔振系統(tǒng)，隔振器組件由2個垂直正交的高剛度流體阻尼隔振器組成，4個隔振器組件協同工作，在保障系統(tǒng)承載能力的同時，可近似實現三向剛度解耦，三向共振頻率相等，且滿足狹小機載空間的安裝尺寸要求。進一步地，考慮負載安裝的影響，采用子結構頻響綜合法建立負載偏心情況下的系統(tǒng)動力學模型，并進行仿真驗證，該模型可反映負載安裝位置對于振動耦合的影響。最后，采用振動臺激勵的方式測量系統(tǒng)三向響應，驗證隔振方案的有效性。

1 三向隔振系統(tǒng)結構與布局設計

1.1 基于流體阻尼的隔振器構型

結合高固有頻率、高損耗因子以及指定頻段傳遞率衰減的設計需求，采用圖1所示隔振器設計構型。

圖1 流體阻尼隔振器原理圖Fig.1 Fluid damping isolator

如圖1所示，頂桿與活塞通過螺紋連接后，串接于膜片彈簧內圓周，由螺母鎖緊為一體，這種分體式設計方便更換不同規(guī)格的膜片及活塞，以調節(jié)隔振器的剛度和阻尼系數。膜片外圓周由壓蓋擰緊固定于剛性外殼上方，利用膜片的軸向撓曲變形提供主剛度。活塞與剛性外殼內壁構成狹小環(huán)形間隙，四周填充有黏性液體介質，當頂桿受力帶動膜片軸向撓曲時，黏性液體將與活塞產生相對運動，產生較大的壓力損失，提供阻尼效果。此外，隔振器下方安裝有層疊式波紋管，輔助彈性元件的引入減小了腔內體積模量，使阻尼力彈性傳遞[14]，近似于在阻尼元件上串聯彈簧。這種特點的隔振器可以用3個包含有剛度、阻尼系數的集中參數來表征，即三參數隔振器。

由于圖1隔振器僅在軸向起阻尼減振效果，需通過多個隔振器在不同方位上的合理組合，來實現系統(tǒng)的多方向隔振，如沿水平方向和豎直方向分別布置相應朝向的隔振器。但問題在于單個隔振器本身具有多方向剛度，除軸向剛度之外，由膜片的面內變形產生的橫向剛度量級也不可忽略。這使得系統(tǒng)沿單一方向的總剛度，是由相同朝向的隔振器軸向剛度與正交方向隔振器橫向剛度的線性疊加，因而系統(tǒng)剛度會明顯大于所設計的隔振剛度。如何消除不同方位隔振器之間的剛度耦合，是隔振系統(tǒng)設計的關鍵。

1.2 基于正交隔振器組件的隔振系統(tǒng)布局

圖2為三向隔振系統(tǒng)布局方案，該系統(tǒng)由負載、4個旋轉布置的隔振器組件以及安裝板組成。其中，隔振器組件由2個正交布置的隔振器組成，隔振器頂桿通過雙向轉接頭連接于負載的各安裝孔處；隔振器底部通過花紋型柔性鉸鏈與基礎連接，這種鉸鏈的橫向剛度較軸向剛度小2個量級以上，因此當隔振器與其構成串聯支路后，橫向剛度大幅降低但軸向剛度近似不變，減小了不同朝向隔振器之間剛度的相互耦合。

圖2 三向隔振系統(tǒng)模型Fig.2 Three-dimensional vibration isolation system

這種由2個正交隔振器柔性連接為一個隔振器組件、再將若干隔振器組件并聯，對負載進行隔振的方式，無需加裝載荷平臺，且安裝和布局更加靈活，有效減小了系統(tǒng)在水面內的外伸尺寸。其中，單個隔振器組件自體質量為0.245 kg，包絡尺寸78 mm×61 mm×63 mm，除底板外的整體尺寸為240 mm×199 mm×101 mm，安裝靜變形量0.44 μm，在確保承載能力的同時，實現了較小的體積和質量。

2 三向隔振系統(tǒng)動力學模型

2.1 三參數隔振模型

首先對單個隔振器進行集中參數建模，如圖3(a)所示:xb,x分別為基礎位移和負載位移；m為負載質量；隔振器視作整體，其動剛度記作Z(s)。則系統(tǒng)在s域上的運動方程簡寫為

(a) 單自由度模型

(b) 三參數隔振器圖3 隔振模型Fig.3 Vibration isolation model

ms2X+Z(X-Xb)=0

(1)

進一步地，由于附加彈簧元件的引入，使1.1節(jié)所述隔振器具有三參數特征，如圖3(b)所示。由串并聯關系，得三參數隔振器動剛度為

(2)

(3)

由于階數增大，當(ω→∞)時，|H(jω)|=O(ω-2)，高頻衰減速率增至40 dB/dec，可一定程度改善因共振峰右移對高頻隔振性能造成的不利影響。

2.2 隔振系統(tǒng)的子結構頻響綜合

在單個隔振器分析基礎上，采用基于頻響函數的子結構綜合法建立隔振系統(tǒng)的動力學模型。當隔振元件之間解除了剛度耦合的情況下，系統(tǒng)的振動耦合主要來自于負載，負載在平臺上的安裝位置不同，會使得系統(tǒng)呈現不同的動力學特性。為此建立了一般安裝情況下(即系統(tǒng)偏心)的整體模型，如圖4所示。

(a) 俯視

(b) 正視圖4 隔振系統(tǒng)簡化模型Fig.4 Simplified model of the vibration isolation system

其中，在4個隔振器安裝點的對稱中心Og處建立全局坐標，過剛體負載質心o建立對齊于全局坐標系的慣性坐標系，使負載的慣量張量對角化，o與Og存在相對偏移(ex,ey,ez)，用Z,2Z分別表示豎向、水平單個隔振器的軸向動剛度，則系統(tǒng)三向平動剛度相等，對于三參數隔振器而言，其動剛度Z即為式(2)。

采用基于頻響函數的子結構綜合法建立系統(tǒng)模型。將整個系統(tǒng)劃分為負載、隔振裝置和安裝板3個子結構，對每個子結構分別進行動力學分析，得到相應的頻響函數矩陣，再根據界面處的力平衡和位移協調關系、以及系統(tǒng)邊界條件綜合各頻響矩陣，得到系統(tǒng)整體的輸入、輸出特性。

系統(tǒng)的子結構劃分,如圖5所示;輸入、輸出矢量定義,如表1所示。

圖5 隔振系統(tǒng)子結構劃分Fig.5 Substructures of vibration isolation system

表1 子結構輸入、輸出矢量定義Tab.1 Inputs and outputs of substructures

將負載視作剛體，輸入輸出的力-位移關系記為

(4)

由剛體負載的受力平衡得到運動微分方程

(5)

式中:m為負載質量;Iu(u=x,y,z)為剛體負載繞相應坐標軸的轉動慣量;(lv,wv)為豎向隔振器安裝距離;(lh,wh)為水平隔振器安裝距離;(x,y,z,φx,φy,φz)為質心的6個自由度。

結合剛體負載運動的合成，得到質心位移與4個安裝點位移的相對關系

(6)

由式(5)、式(6)整理可得式(4)中矩陣的各元素表達式。

隔振裝置由8個集中參數隔振器構成，由于隔振器內部不計慣量，則輸入、輸出力相等，而力的大小等于兩端位移差與隔振器位移阻抗Zi的乘積，則對于單個隔振器有

(7)

將8個隔振器的頻響矩陣按順序組集，得到隔振裝置整體的輸入、輸出關系

(8)

式中，Hy=diag(1/Z1,1/Z2,…,1/Z8)，為8個隔振器的位移導納矩陣。

安裝板以固連于基礎的任意位置為參考點，其四端參數方程滿足

(9)

對柔性安裝板而言，由于幾何形狀的不規(guī)則，需通過在物理坐標上依次作用激振力的方式，逐個測定式(9)中矩陣中的導納。而若僅考慮剛性安裝板，注意到輸入、輸出關系可視作剛體負載子結構的反向連接，此時可令

(10)

對于消極隔振而言，剛體負載的外部作用力為0，并結合各子結構交界面處的連續(xù)性條件

(11)

聯立式(4)、式(8)、式(9)、式(11)消去力矢量，整理可得從安裝板參考點位移到剛性負載質心位移的傳遞函數矩陣

XI,m=H12,m(H22,m-Hy-H11,b+

(12)

式(12)中的Gs即為以基礎六向運動為輸入、負載六向運動為輸出的系統(tǒng)傳遞函數矩陣。若負載質心存在偏移，以質心與安裝中心不等高為例，即ex=ez=0，ey≠0時，討論負載安裝位置對系統(tǒng)動力學耦合的影響，式(12)整理為

(13)

其中

由于偏心距ey的引入，使傳函矩陣產生與ey線性相關非對角項，從幾個對角元素出現的位置可知，當沿耦合自由度方向作用基礎激勵時，會同時引起負載在2個關聯方向的振動響應，即負載沿x軸的線運動與繞z軸的搖擺同時存在，沿z軸的線運動與繞x軸的搖擺相互耦合。類推地，當負載存在偏心距ex時，也可得出類似結論。因此，在負載安裝時，應當注意調節(jié)消除質心與安裝中心的偏心距。

2.3 系統(tǒng)模型的有限元驗證

為驗證2.2節(jié)模型計算結果過程的準確性，建立如圖6所示的有限元模型。其中，負載和安裝板采用C3D20R實體單元，負載質量為4 kg，負載偏心距ey=20 mm，單個隔振器主軸方向采用2個Spring單元和1個Dashpot單元表征三參數物理模型性質，其中k1=6×105N/m，k2=2.7×106N/m，c=50 Ns/m，水平布置的隔振器數值設為豎向的2倍，此外，在單個隔振器垂直主軸方向設置徑向剛度，用以模擬隔振器的橫向傳遞特性，隔振器底部與安裝座接觸位置定義Coupling約束，釋放除端面法向位移外的全部自由度，使運動只沿主軸方向傳遞。沿安裝板中心施加3個方向上的單位位移激勵(xb,yb,zb)T=(1,1,1)T，分析頻率范圍為0～500 Hz，計算提取質心的位移頻響，并與2.2節(jié)理論模型計算結果作對比，如圖7所示。

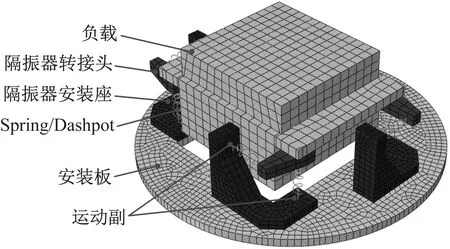
圖6 隔振系統(tǒng)有限元模型Fig.6 The FE model of isolation system

(a) x

(b) y

(c) z圖7 隔振系統(tǒng)頻響對比Fig.7 Frequency responses of isolation system

可以看出，當負載質心與隔振器安裝平面不在同一高度時，由于水平隔振器傳遞的橫向力對負載產生附加力矩，引起負載的搖擺振動，表現在傳遞特性曲線中出現2個共振峰:第一個共振頻率為線振動頻率;第二個共振頻率為角振動頻率。二階共振峰的出現使高頻段隔振性能變差，且誘發(fā)的搖擺振動易對負載的工作精度產生顯著影響。通過對比由子結構頻響綜合法建立的系統(tǒng)模型及有限元模型的計算結果，曲線在分析頻段內基本吻合，表明該理論建模方法是準確有效的，可以用于研究分析圖2所示布局的隔振裝置攜帶負載進行工作時，各自由度間的動力學耦合及系統(tǒng)的振動傳遞特性。

3 三向隔振系統(tǒng)隔振效果測試

為驗證隔振方案的有效性，搭建如圖8所示的試驗系統(tǒng)進行測試振動傳遞性能。其中，隔振裝置安裝于負載與振動臺之間，振動臺臺面及負載頂部各布置一個加速度傳感器，控制臺面產生0～300 Hz頻帶的白噪聲激勵，使臺面產生隨機振動，2個加速度計測得的振動信號輸出至數據采集與分析儀做分析處理，得到振動傳遞特性曲線。

圖8 振動傳遞率測試原理圖Fig.8 Scheme of vibration transmissibility measurement

試驗基本思路是：先配置滿足性能要求的8個隔振器，再組裝成隔振系統(tǒng)進行整體的振動傳遞測試。下面以圖8為基本框架，分別對單個隔振器以及隔振系統(tǒng)整體進行試驗。

3.1 隔振器振動傳遞特性

現場安裝如圖9所示，將標準配重塊作為單個隔振器的負載，通過更換不同質量，可以看到隔振器滿足三參數物理模型的振動傳遞規(guī)律，如圖10所示。

圖9 隔振器試驗Fig.9 Measurement of each vibration isolator

圖10 質量改變對振動傳遞特性的影響Fig.10 Impact on transmissibility by changing the isolated mass

其中實線部分為實測結果，虛線部分為根據式(3)得到的理論曲線。從變化趨勢可知，隨質量的減小，共振峰逐漸右移，共振幅值出現先減小后增大的現象，這種規(guī)律滿足三參數物理模型的性質，即當質量取某一中間值時，存在最優(yōu)的系統(tǒng)阻尼比，使共振峰值最小[15]。而實測與理論曲線趨勢的一致性也驗證了該構型的流體阻尼隔振器具有三參數隔振的物理性質。

8個隔振器單獨測得的傳遞特性曲線，如圖11所示。用于豎向支承的隔振器負載質量為1 kg，用于水平支承的隔振器負載質量為2 kg。8條傳遞特性曲線基本一致，其中共振頻率在120 Hz附近，共振幅值在5～7 dB以內。

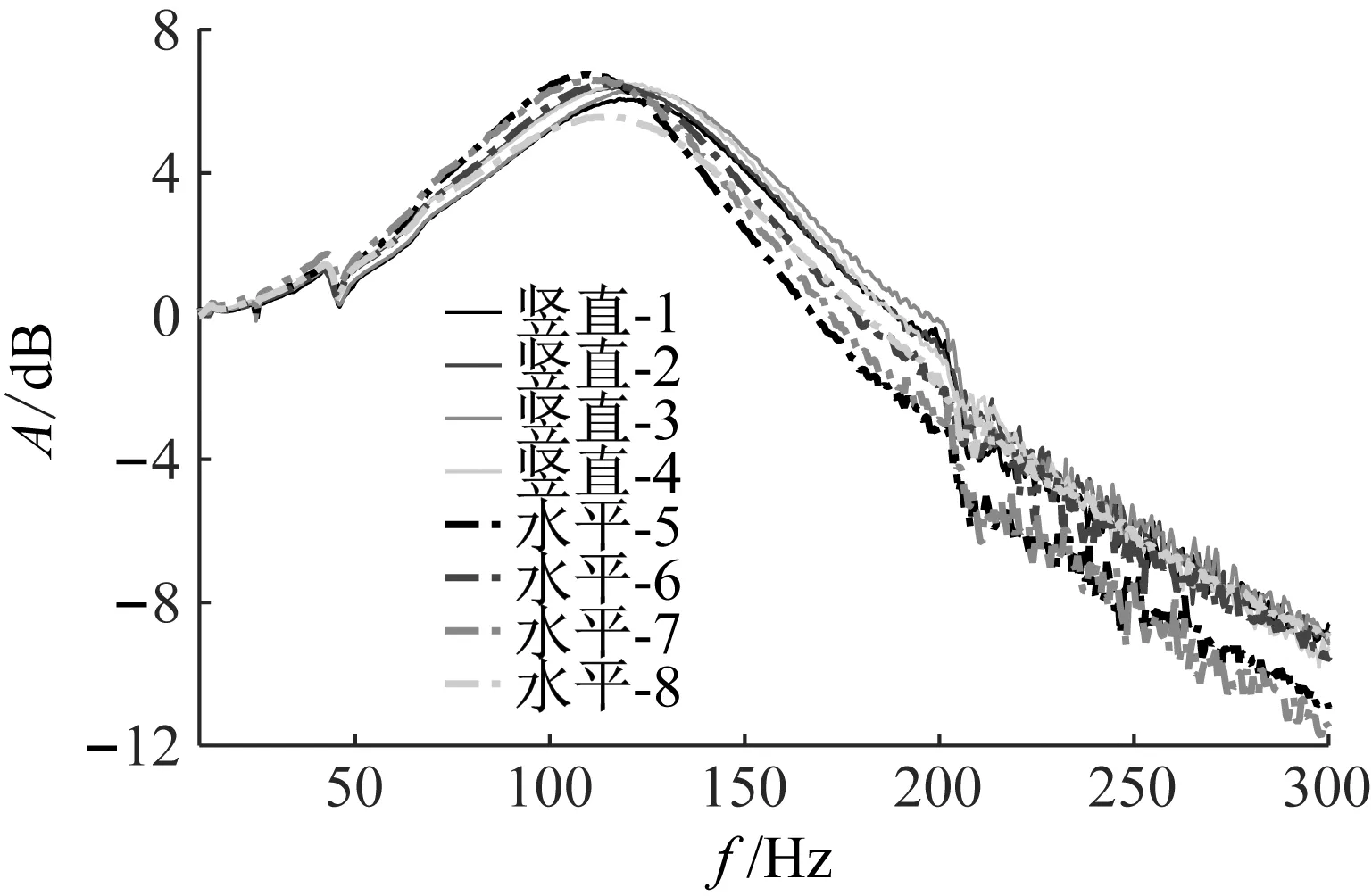
圖11 單個隔振器的振動傳遞率Fig.11 Transmissibility curves of eight isolators

3.2 隔振系統(tǒng)的三向隔振效果

將3.1節(jié)中調試好的隔振器組裝成隔振器組件，安裝于4 kg負載的4個安裝孔位置，其中負載質心高度與隔振器安裝高度一致，以消除振動耦合的影響，分別控制振動臺施加3個方向的白噪聲激勵，進行系統(tǒng)傳遞特性測試，圖12為水平激勵時，現場的安裝布置。

圖12 隔振系統(tǒng)傳遞特性測試Fig.12 Measurement of the system’s transmissibility

由圖13可知，系統(tǒng)沿3個平動方向的共振頻率及共振放大倍數分別為：x方向(117 Hz,8.64 dB)，y向(112 Hz,6.16 dB)，z方向(113 Hz,6.96 dB)，測試頻段內無二階共振峰出現，高頻共振抑制效果明顯，同時400 Hz處的振動衰減>10 dB，目標頻率后的傳遞率數值滿足隔振需求。

圖13 系統(tǒng)的三向振動傳遞率Fig.13 System transmissibility curves in three directions

4 結 論

本文研究一種高固有頻率的機載設備三向隔振系統(tǒng)，為適應狹窄尺寸空間和滿足承載能力要求，將固有頻率提升至100 Hz以上，使系統(tǒng)獲得較小的靜態(tài)變形。采用大剛度膜片彈簧、間隙式阻尼結構和焊接波紋管設計了三參數隔振器。為滿足系統(tǒng)三向隔振頻率相等的要求，采用2個隔振器正交組合為隔振組件、4個隔振組件旋轉對稱分布的方式對負載進行隔振。基于子結構頻響綜合法建立了隔振系統(tǒng)動力學模型，研究隔振系統(tǒng)攜帶負載時，負載位置不同對于整體振動傳遞的影響，計算結果表明載荷質心與隔振裝置安裝中心的相對偏離是引起振動耦合的原因。在振動試驗臺上測試了隔振系統(tǒng)3個平動方向的振動傳遞性能，實測三向共振頻率在115 Hz附近，共振放大在6.0～8.6 dB，且 400 Hz處的振動衰減>10 dB。文中提出的隔振系統(tǒng)構型設計可應用于對承載能力、安裝空間和共振放大因子具有較高要求的使用場合。