基于外部認知負荷理論下數學符號邏輯認知順序探究
張學林,任全紅
(綿陽師范學院數理學院,四川綿陽 621000)
0 引言
認知負荷指學習者為了完成所給認知任務,在工作記憶上進行的心智活動所需的全部心智能量.這個理論是由澳大利亞教育心理學家John Sweller等人在上世紀80年代提出的,他們將認知負荷分為三種類型:外在認知負荷、內在認知負荷和相關認知負荷.內部認知負荷是元素間交互形成的負荷,它取決于所需學習的材料的本質與學習者的學科知識之間的交互,教學設計是否得當能不能對它產生直接的影響.而外部認知負荷是超越內部認知負荷的額外負荷,它主要是由教師教學設計不當引起的.“由教學設計引起的工作記憶稱為外在認知負荷,外在負荷是可以改變材料呈現方式來改變的”[1].因此學生在初學數學符號、數學公式時教師教學一定要呈現數學符號書寫邏輯順序,有利于學生的主動建構.為此,本文僅從數學符號簡述、數學符號不規范和規范的書寫順序的教學、建立和培養學生數學符號意識的教學策略建議等三個方面進行論述,提高數學教學效果.
1 數學符號簡述
(1)“數學符號意識主要是指能夠理解并且運用符號表示數、數量關系和變化規律;知道使用符號可以進行運算和推理,得到的結論具有一般性.”[2]
(2)“符號是文化與傳播數學思想的媒體,世界各國都有各自的語言,如漢語、英語、德語、法語……,但數學符號可以世界通用,全世界的人只要受過初等教育都認識下列符號語言,不需翻譯如:2+3=5;(a+b)2=a2+2ab+b2;ΔABC∽ΔDEF……”.[3]
(3)“數學符號是數學文獻中用以表示數學概念,數學關系等的記號.”數學符號包括幾何符號、代數符號、運算符號、集合符號、特殊符號、推理符號、數量符號、關系符號、結合符號、性質符號、省略符號、排列組合符號、離散數學符號等符號,各有各的表示.
為了讓學生更容易理解數學符號,筆者認為數學符號是用來表示數學概念、定義、定理、公式、數量(式)間的關系及其運算與推理,從而更方便解決實際問題所用到的符號.“建立符號意識,有助于學生理解符號的意義并進行數學思考.在解決問題中,使學生經歷符號化的過程.”[4]
2 培養數學符號的意義
“符號意識作為數學重要的學習內容之一,建立符號意識有助于學生理解符號的使用是數學表達和進行數學思考的重要形式.”[2]培養和提高學生的數學符號意義獲得能力是解決“數學難學”“數學枯燥”“聽而不懂”“懂而不會”“會而不對”等教學難題的一種有效的、可行的、具有操作性的途徑和方法.對學生提升數學運算素養、提高邏輯推理能力、提升代數思維、培養學生建模能力等方面具有重要的意義,因此,初次教學數學符號時一定要讓學生認知數學符號的意義、出現的邏輯順序以及理解利用數學符號解決數學問題的作用,培養學生的符號意識.
3 初次教學數學符號時出現不規范的書寫順序及矯正
“在教學過程中應盡可能減少外部認知負荷,注意學習材料的呈現方式和教學設計水平有關,呈現形式越合理,越符合學習者的認知水平,學習者的信息加工的干擾因素越少,外在負荷就越低,有利于學習.”[5]學生在沒有主動建構數學符號的意義情況下初學數學符號時,要特別注意書寫數學符號順序,體現數學的邏輯性,否則會增加學生的外在認知負荷,教師在教學時對數學符號的書寫順序,如采用漢字從左自右的順序,易造成學生對數學符號、知識理解困難,缺乏邏輯.因此學生初學時數學教師一定要按照數學邏輯結構書寫數學符號,引導學生主動建構,初步形成數感,感受數學符號的作用,初步養成樂于思考、勇于質疑、實事求是等良好品質,不能采取漢字從左自右的書寫順序,避免學生對數學符號不理解,先后的邏輯混亂,造成學生對數學符號產生厭倦,增加學生對數學符號的認知負荷.
(1)學生在學習加法時,教學生運用加法符號“+”時,比如“3與2的和”列數學算式時:不應該從左自右的順序:書寫3+2;應該先寫3與2,再寫中間的“+”.同理其它幾種運算符號也應該這樣列式書寫,培養學生數學的邏輯思維.一般的老師教學時是按照從左自右的順序書寫算式或解析式.
(2)在學習分數時,應該先寫分子、分母,最后寫分數線,一般的老師教學時是按照分數線、分母、分子的順序書寫,缺乏邏輯性.
(3)在學習百分數時,讓學生真正弄懂百分數的同時,明確百分數的書寫順序,比如82%.按照邏輯順序應該是先寫%,再寫82,不應該是先寫82,再寫%.
(5)在學習絕對值符號時,應該先寫數或表示數的字母(或代數式),再寫絕對值符號,比如求-5的絕對值的書寫順序,應該是先寫-5,再寫絕對值符號,即:-5→||.不應該按照||→-5的順序.
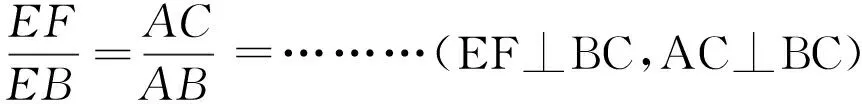
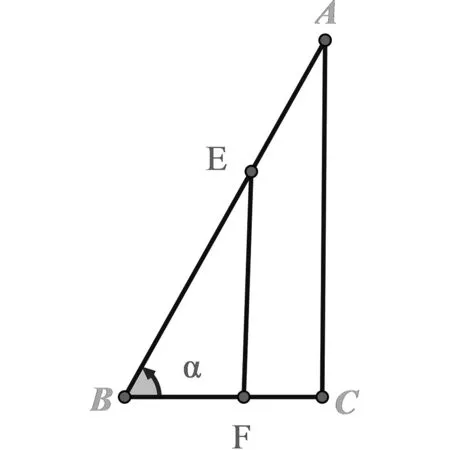
圖1 示意圖Fig.1 Schematic
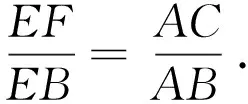
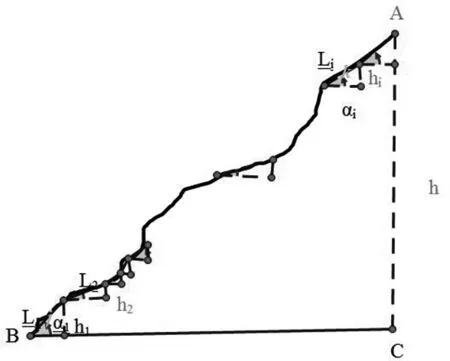
圖2 示意圖Fig.2 Schematic
(8)在初學某些乘法公式時,也要注意書寫順序,如在學習和的完全平方公式時,其書寫順序為:(a+b)2=a2+2ab+b2,右邊的書寫順序為:a2、b2、+、2ab,這與語言文字“兩數和的完全平方等于兩書的平方和再加上兩數積的兩倍”相一致.
(9)注意極限符號的引入,比如在計算山高AC的長度時,運用“化整為零、積零成整”的數學思想,首先將曲線山坡化為首尾相接線段L1、L2、……、Ln,AC=h1+h2+......+hn=L1Sinα1+L2Sinα2+……+
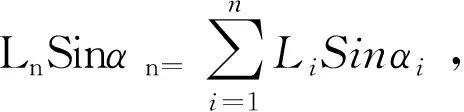
其認知順序應該是:
的邏輯認知順序或書寫順序如圖2.
4 培養學生主動建構數學符號邏輯認知意識教學策略
“突出知識的形成過程.課程內容的組織要重視過程,處理好過程與結果的關系;課程內容的呈現應注意層次性和多樣性.符號意識是將實際問題轉化為數學模型問題的基礎.”[2]培養學生符號書寫邏輯順序是突出知識的形成過程的一種表象.
4.1 讓學生進一步明確數學符號的真正含義

對中小學生來說運用符號不是一件很容易的事,這是因為符號化有一個從具體—表象—抽象—符號化的過程.為此,必須加強數學符號的教學,逐步培養中小學生數學符號邏輯思維能力.
4.2 在教學中注重材料的呈現及數學符號學習的探究過程
教學中特別要注重有關數學符號材料的呈現方式及探究過程,“工作記憶負荷不僅受學生活動的影響,還受材料的內在本質材料呈現形式的影響.”[6]比如在呈現“一只青蛙四條腿,二只青蛙八條腿,三只青蛙十二條腿,問十只青蛙幾條腿?”時,應該以詩詞的方式呈現學生容易理解:
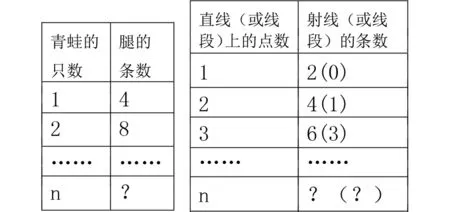
(利用表格形式進行探究降低學生外在認知負荷)
一只青蛙四條腿,
二只青蛙八條腿,
三只青蛙十二條腿,
……
問十只青蛙幾條腿?
同時特別注重數學符號的探究過程,英國著名教育家豪森(A.G.Howson)所指出:“沒有必要引入任何符號或縮寫,除非學生自己已經深深感受到這樣做的必要性,以致于他們自己提出這個方面的建議,或至少當老師提供給他們時他們能夠充分體會到它的優越性”.[7]因此在教學中要引導學生探究數學符號的形成過程,讓學生真正能感受到引入數學符號的必要.比如學生在學習用字母表示數時,從特殊到一般進行探究,在上述例子中引導學生進一步探究:n只青蛙幾條腿?一條直線有一個點有兩條射線,兩個點有幾條射線?n點有幾條射線?如果改為線段呢?應該列出表格,引導學生探究.在學習am·an=am+n時要讓學生明確乘方的意義,將乘方改為乘法,由不完全歸納法猜出同底冪的乘法公式后,再由am=a×a×a×……×a(m個a相乘)乘法和乘方互相轉化進行嚴密的邏輯證明.
4.3 鼓勵學生利用模型思想中的數學符號解決生活中的實際問題
要鼓勵學生習慣使用數學符號解決生活實際問題,提高效率,特別是數學建模的有關問題,使用數學符號尤為重要.“數學建模是對現實問題進行數學抽象,用數學語言表達問題、用數學方法構建模型解決問題的素養.數學建模過程主要包括:在實際情境中從數學的視角發現問題、提出問題,分析問題、建立模型、計算求解,檢驗結果、改進模型,最終解決實際問題.”[8]
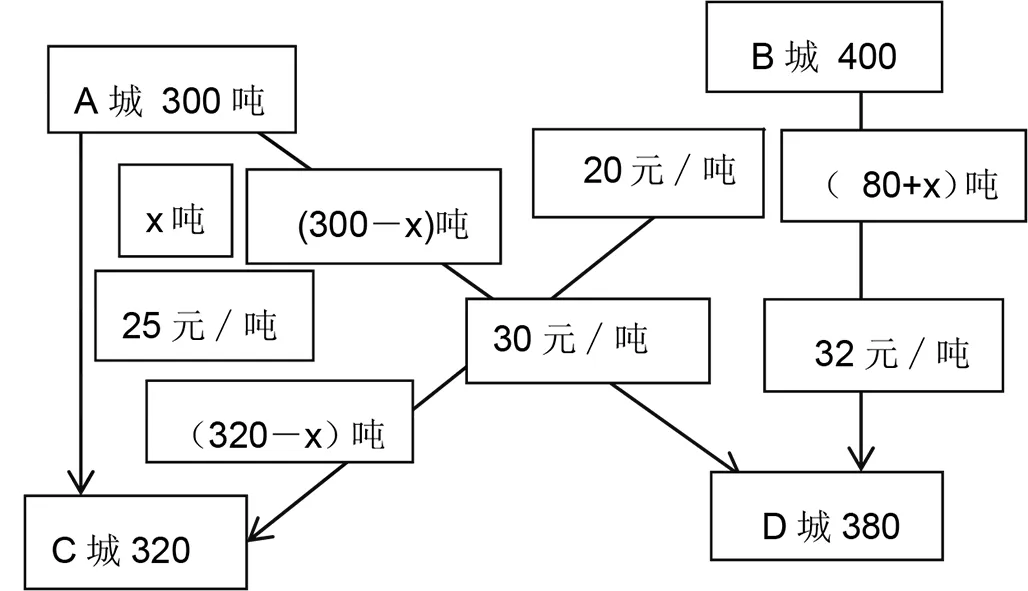
圖3 數學計算模型Fig.3 Mathematical calculation model
例 A地有蔬菜300噸,B地有蔬菜400噸,現要把蔬菜運往C、D兩市;如果從A城運往C、D兩市運費分別為每噸25元和30元,從B地運往C、D兩市運費分別為每噸20元和32元;現已知C地需要320噸,D地需要380噸.如果某個體戶承包了這項運輸任務,怎樣的運輸方案花錢最少?
分析:引導學生利用字母、箭頭、方框圖等數學符號表示的數學模型將生活中的實際問題轉化為數學問題,再利用數學符號列出解析式,建立數學模型,從而求解.
y=25x+30(300-x)+20(320-x)+32(80+x),即y=7x+17 960.
由題意得,x≥0,(300-x)≥0,(320-x)≥0,(80+x)≥0;解得0≤x≤300,當x=0時,ymin=17 960.
教師這樣進行教學設計就大大地降低了學生外在認知負荷.
4.4 通過練習加以強化數學符號的使用,進一步強化數學符號的意義
4.5 遵循學生的認知能力,逐步培養學生數學符號意識
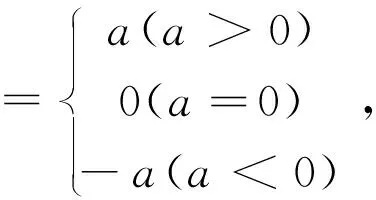
5 結語
總之,教師在面對學生學習新知識,初次教學數學符號時一定要仔細進行教學設計,注重數學知識的邏輯結構,根據邏輯結構確定數學符號的書寫順序,讓學生進一步建構認知順寫,減少學生外在認知負荷,激發學生學習數學的興趣,提高數學教育教學效果.

