網絡計量學和替代計量學的挑戰及其社會影響的穩健和非穩健計量評價

劉廷元，劉紓曼

（西南石油大學圖書館，成都 610500）

1 引言

科學成果的社會影響評價是廣義科學成果評價的一部分。傳統形式的狹義科學成果評價主要是建立在文獻計量學、科學計量學的期刊引文指標之上，以學術影響測度為主。新興形式的廣義科學成果評價，將其擴展到網絡計量學、替代計量學的關注-使用指標之上，以社會影響測度為主。

目前，基于網絡計量學（webometrics）、替代計量學（altmetrics）的科學成果計量，到底是選擇學術影響還是社會影響的路徑，不同學者有不同的觀點和認識。altmetrics一詞的創立者Priem等[1-2]認為，應當選擇“基于在線工具及環境活動的學術影響計量”路徑，重點關注Twitter和Facebook等社交媒體上的轉載數據。Priem[3]對altmetrics的定義，不但將學術影響包含在不斷變化的工具和數據聚合環境活動中，而且還包含了將其定位為網絡計量學的一個分支。

然而，由于網絡計量學、替代計量學的影響計量與傳統形式的影響計量存在較大差異，有的甚至不相關，導致影響的內涵及其計量方法備受爭議[4-5]。altmetrics或alternative metrics術語中的“替代”即“alt(ernative)”也經常受到批評，因為大多數實證研究都表明，替代計量學視角下的影響與傳統計量形式的影響相比，不但相關性很弱而且可靠性和穩定性也沒有得到很好解決，只能被視為一種補充而不是“替代”。這就導致一些學者將學術引文指標和社交媒體指標從總括性的影響術語中分解出來[6-7]，將它們定義為相互補充而不是相互替代的影響研究，即所謂的學術維度和社會維度[8-9]。而另外一些學者，則只將影響看作文化或社會方面的共鳴，即影響不再被視為科學成果學術質量的代表，而是在更廣的意義上被定義和使用[10]。因此，用于分析和提供科學影響數據的網絡計量學和替代計量學，也被定義為“基于社會網絡的新指標的創建和研究”[11]。

對于網絡計量而言，Ingwersen[12]提議采用類似于引文分析的網絡影響因子（web impact factor，WIF；包括外鏈數、內鏈數和總鏈數指標）來計算社會網絡的影響，并將網絡計量學定義為研究網絡信息資源、結構和技術的構建與使用的定量方面[13]。然而，社會網絡影響的復雜性大大超過了多源數據計量的相對簡單的信息計量方法，使傳統的網絡計量很難對多種網絡的深層使用信息（如情境數據）進行統一的分析、評價，需要建立一種以多源數據聚合為目標的新計量框架。經過Adie等[11]的研究，特別是多種網絡和社交平臺的關注-使用指標的創建，提出一種通過提及、推薦、共享、收藏等指標進行加權計數的“altmetric關注分數”（at‐tention score）來計算社會網絡的影響。對于替代計量而言，Adie及其合作者Roe等提出的“altmetric關注分數”和“altmetric分數”，成功地結合情境指標數據，如作者、內容、情感等，對研究成果的各種社會影響進行深層計量評價[11]。一般而言，論文、論著的在線討論、分享、收藏等關注-使用越多，指標的權重越大，altmetric分數越高。因而，從維度和質量上看，替代計量的社會影響分析比之前的其他任何一種計量都更復雜。因為替代計量的來源數據及其權重都具有主觀成分，更重要的是，它還存在多種維度的局限和缺陷，例如，普遍存在計數/分數為0，以及因為涉及利益相關者，普遍存在原始計數的多種不規則性，從而使原始數據對一些成果的影響評價幾乎沒有什么區分能力，對成果的評估任務也沒有什么用處[14]，計量評價的可靠性和穩定性難度大大增加。

盡管替代計量具有許多局限和缺陷，但替代計量指標的豐富情境遠比網絡計量指標的單純計數能給人更多的啟發。按Bj?rneborn等[13]的解釋，網絡計量是超鏈接的數量和類型、萬維網的結構和使用模式的計量，它可以告訴我們，某個網站從其他網站接收鏈接的網頁數量與該網站發布的可供訪問的網頁數量，即表層使用頻率的網絡影響因子[12]或其他社會影響因子等。替代計量則是來自各種網站接收訪問的非常多樣化的網絡關注-使用數量的計量，它可以告訴我們網站發布的網頁（研究成果及其論文、論著）在社會網絡中具體應用的傳播數量，即深層使用頻率的altmetric分數[11]或社交媒體指數（social media index）等[15]。因此，替代計量是對表層網絡使用信息的深層應用分析，是對網絡計量的更大補充和發展，二者不是兩個完全不同或對立的信息計量分析體系。網絡計量和替代計量是廣義信息計量學發展的兩個必然階段，本質上屬于一個統一的網絡信息分析整體，即一個統一的廣義信息計量學分支。基于此，二者可以并稱為網絡-替代計量或網絡-替代計量學。

在本研究中，我們對網絡環境下國家社會科學基金（簡稱“國家社科基金”）項目成果的社會影響數據進行了廣泛采集和分析，特別關注網絡-替代計量指標數據和計量評價的穩健性。這里，重要而又不能回避的問題是，網絡-替代計量指標數據本身存在多種不確定和不完備的局限或缺陷，尤其是高零值（左側）、多異常值（右側）和極端右偏斜分布之間的復雜關系，以及由此帶來的計量敏感和失效風險，使社會影響的計量評價在數據、方法和結果等方面都面臨巨大挑戰。解決這些問題的基本思路是利用穩健計量方法消除或削弱高零值、多異常值和極端右偏斜分布對一般信息計量和中心信息計量分布趨勢的干擾，即通過四分位零值縮減法進行抗差性檢定（左），通過縮尾求穩方法進行異常值合理修正（右），以及通過縮尾均值對偏斜分布數據進行穩健的無量綱化和綜合評價。由于傳統回歸模型是基于信息計量分布的正態性（對稱性）和規則性（均勻性）假設，對數據普遍存在的計數為0（非對稱性）及其他不規則性外圍和異常子群（異常值或對稱/非對稱輕尾/重尾）高度敏感[16]，信息計量模型及其數據擬合的抗差性、可靠性和穩定性都不高。因此我們將對數據集的非正態不規則分布外圍及其異常子群不具有抗差性、可靠性和穩定性或抵抗作用的一般計量方法，稱為非穩健計量；將對數據集的非正態不規則分布外圍及其異常子群具有抗差性、可靠性和穩定性或抵抗作用的有效計量方法，尤其是對零膨脹（高零值）、多異常值（高杠桿）、極端右偏斜（重尾）和污染數據具有抵抗作用的計量方法，稱為穩健計量。

在此方法基礎上，以四川省2005—2014年驗收通過的341項國家社科基金項目成果的社會影響數據，應用穩健的計量評價方法進行實證研究。需要說明的是，因國外網絡和社交媒體中的國家社科基金項目成果數據較少，且與國內數據的相關性較差，本研究未予以采集；社會影響的時間累積效應因素，因需要專門的時序動態響應計量方法也未涉及。

2 網絡計量學和替代計量學的社會影響評價挑戰

對于以網絡-替代計量指標數據為基礎的社會影響評價而言，最重要而又不能回避的挑戰是原始數據集的不確定和不完備缺陷；尤其是高零值（左側）、多異常值（右側）和極端右偏斜分布及其非穩健方法可能帶來的計量失效風險，已經大大超過了早期信息計量學在指標創建和研究時遇到的“測度惡魔”：隨機性、模糊性和顯著歧義性[17]。以網絡計量學和替代計量學為代表的現代信息計量學試圖將科學成果的社會影響評價，搭建在一種多維度的網絡信息活動上，并以豐富的網絡關注-使用指標數據來測度科學的社會影響。然而，網絡環境下的社會影響計量，涉及不同的利益相關者和技術平臺，數據產生、使用和擴散的動機、行為高度復雜，要實現真實、合理和公正的反映，如科學成果在網絡上的關注、使用、下載、分享、提及、閱讀、評論等指標，達到類似于傳統引文學術影響的抗差性、可靠性和穩定性，首先面臨兩大挑戰。

2.1 左側挑戰：高零值和零膨脹分布

對于社會影響計量來說，可用網絡-替代數據集的高零值（即“低覆蓋”，信息計量學者習慣用“覆蓋率”代替“零值率”）問題是一個非常獨特的重大挑戰。由于低零值意味著置信區間即使是保守的、穩健的，也能覆蓋真實參數[18]。相反，在高零值分布下，樣本的置信區間即使是保守的、穩健的，也會對數據集的真實性、合理性及其分布偏差和誤差造成很大影響，從而大大減少或削弱信息計量方法和結果的抗差性。

零值率等于1減去覆蓋率之差，對覆蓋率的定義一定意義上也是零值率的定義。對于覆蓋率，信息計量學有兩種不同的角度。Haustein等[19]從“有”的角度出發，將覆蓋率定義為：特定平臺上至少有一個提及的文檔的百分比；Thelwall[20]從“無”的角度出發，將覆蓋率定義為：無零值的產出比例。無論從何種角度定義，覆蓋率都繞不開“零值率”，因為高覆蓋率意味著“0”值低（少），低覆蓋率意味著“0”值高（多）。

Mas-Bleda等[21]對西班牙和英國8個學科的調查結果顯示，網絡-替代數據中Mendeley的覆蓋率最高，80%的抽樣文章擁有一個或多個Mendeley讀者，其次是Twitter（34%），其余來源的覆蓋率則低于3%。許多跟蹤調查發現，一些科學成果在提及和社交媒體中能追蹤到的信號數量很少或幾乎不存在，具體的實踐中也存在同樣的困難[22]。Sugimoto等[23]在綜述中提到Gorraiz等人的4篇文獻調查結果，發現F1000的覆蓋率研究相對較少，已有的覆蓋率調查從小于1%到2%～8%不等。Gl?nzel等[24]發現，在公共衛生領域的12項指標中，零值率的比例最高的達到78.7%（捕獲），最低的為1.4%（提及），大多數則接近50%。Chi等[22]指出，在自然科學中，與生命科學或社會科學相比，這些指標類別的覆蓋率或數據可用性的百分比還要低。

社會影響指標變量中的高零值，使數據集中心部分的左側產生大量的無影響數據。零值率超過50%時，會形成嚴重的零膨脹（zero-inflated）分布，導致有影響的信息計量分布向右過度偏斜，使高零值下的影響計量面臨一般信息計量和中心信息計量分布的抗差性和一致性大大減少或削弱的挑戰。從多指標變量的“嚴密分析”角度看，高零值不能全截斷，也不宜隨意切尾或刪除，因為每個變量的零值率、偏度不同，單側分位點意義也不同，樣本的置信區間及其結構信息含義也不同。

2.2 右側挑戰：多異常值和極端右偏斜分布

與傳統的學術影響指標相比，社會影響指標的計數和分數更容易受到人為干擾，被個人、機構及其自動賬戶（機器人）操縱，產生網絡-替代數據的作弊即蓄意污染；尤其是在科學成果的社會影響成為評價指標之后，一些行為不端者、中介、商業機構出于相關利益驅使、游戲化（遵循坎貝爾定律）及惡意心理，會試圖通過某些數據點的超級放大（極端異常值）來提高或破壞科學相關者的影響地位。對社會影響的異常子群即多異常值，如果全截斷或部分切尾/刪除，信息計量的完整性會受到潛在威脅；但如果全保留，就會使一般信息計量和中心信息計量的分布趨勢發生潛在扭曲[25]。因而，多異常值和極端右偏斜分布，會對數據集的真實性、合理性及其計量方法和結果的可靠性與穩定性造成嚴重影響或損害，從而給計量評價的穩健性帶來巨大挑戰。

此外，由于網絡-替代數據的來源、內容、標識、粒度、精度及其學科覆蓋并不十分清晰和確定，或者數據調查者和分析者的質量保證與科學能力不足，未能進行嚴格、規范和統一的技術性控制，給數量眾多的多源數據的挖掘、聚合、清洗、提取、檢測等帶來諸多技術疏漏，本身也容易產生數據的高意外污染，出現系統性異常子群，或大量的零值、缺失值、錯誤值。因而，數據處理技術的可靠性和穩定性也會對計量數據的分布及其真實性、合理性造成嚴重影響或損害，有時甚至成為一種關鍵挑戰。

就前者而言，蓄意污染會直接導致數據集的均值、極大值偏高或超高，以致出現杠桿性污染；就后者而言，意外污染則直接導致指標值的均值、標準差和方差的不真實或不穩定，以致出現系統性污染。所以，數據集的右側不論是蓄意污染還是意外污染，都會給社會影響的真實性、合理性及其信息計量方法的可靠性和穩定性帶來諸多問題；因為遠離中心或偏離一般分布模式的多異常值，一旦出現在指標數據集中，如果不采取可靠的穩健計量方法，就會使評價模型產生壞解，導致非正態不規則分布外圍及其異常子群計量出現高度偏差和誤差。理論和實證研究很容易證明，在非穩健模型中，即使一個孤立點也會對數據集產生扭曲性的影響。

由于一般計量數據普遍存在的信息計量分布特征也是右偏態分布，網絡-替代計量指標中的多異常值，會將這種向右偏斜的不對稱特征進一步放大，并與數據集左側的零膨脹分布共同作用，將這種過度右偏斜的不對稱特征超級放大，從而成為極端右偏斜分布，使社會影響的計量面臨更大的挑戰。

3 網絡計量學和替代計量學的穩健方法

對于以指標觀測數據為對象的計量學來說，高零值和多異常值在什么條件下是“真實的”（true），可以作為樣本值進行合理的保留或修正，在什么條件下是“過度的”（extra），只能作為結構值，即一定條件下對“結構性（真實）零”[26]進行適度的截斷或隱匿，是現代信息計量學發展的重要基礎。30年前，加拿大學者Tague-Sutcliffe[27]在紀念情報學家布魯克斯（Brookes）的文章中說，Brookes曾對等級模型中的長尾（long tails）隱匿感到非常不解，因為用大小-頻率方法將長尾全截斷（隱匿）過于簡單，存在嚴重的結構信息丟失。這個問題一直到“五計學”的今天，仍未徹底解決。例如，在信息計量學的研究中，普遍調查分析網絡-替代指標的低覆蓋（基于學科、主題、地區等）[19-23]，卻不對已經產生的高零值計量困境進行實質性的數理分析；普遍調查分析指標無零值的密度[28-29]，卻不對指標有零值的強度進行關聯性的計量評價。后者本應該與前者并列，但在這些文獻中都不提及。顯然，在覆蓋率和密度的研究中，已有文獻對零值、近零值及其長尾分布，其實是在進行結構性的截斷或隱匿，盡管大都是無意識的。然而，當來源數據普遍存在零過多、異常值和過度離散時，即使樣本的置信區間是保守的、穩健的，信息計量分布及其異常值檢測的抗差性也會大大降低或不具有抗差性，這時如果進行樣本性全保留或結構性全截斷，都會給計量評價造成極大損害。在數理統計及相關研究中，通常基于零膨脹模型，把零值看作“真實的”和“過度的”兩個不同質的群組，即分為零計數和非零計數兩個子集，從總體混合概率分布上進行研究[30]。然而，如果數據集存在多異常值，基于不同計數模型的混合概率必然受到影響，其“真實的零值”和“過度的零值”擬合數據也不可靠。因此，網絡計量學和替代計量學在研究高零值、異常值和極端右偏斜分布時，必須在信息計量分布的保留、截斷或修正、隱匿的條件和方法上找到自己的科學起點和出路。

3.1 基于左側高零值和零膨脹分布的穩健方法

信息計量學的大多數原始數據集，并不滿足異常值識別的先驗假設：正態性、規則性。如上文所述左側挑戰[24]及相關文獻[31-32]中報道，許多指標數據集的零值率（Zr）在50%左右，即使不考慮右側多異常值，也是典型的零膨脹過度右偏斜分布。以異常值檢測抗差性較好的四分位法為例，當Zr在75%左右時，是典型的零膨脹極端右偏斜分布，它直接導致Q3=Q1=0即四分位距（inter-quartile range，IQR）等于0，或接近于0，樣本箱線圖的圖框中線將不起作用，觀測值的IQR檢測完全失效即檢測不出異常值。另外，零膨脹產生的非均勻右偏斜分布，還使最終的多指標綜合評價很容易受到異常值的干擾。由于零膨脹對中高分位的下限和上限影響很大，因此，原始數據集左側的抗差性檢定對異常值的識別和修正非常重要。

如果數據集的Zr＜25%，即Q1＞0，根據統計學的樣本置信區間理論和零膨脹樣本結構理論，數據樣本的抗差性較好，低分位零值可以作為“樣本性零”保留，盡管其中也可能有非真實的零，但因危險率小可以忽略，因此低分位零值的保留系數為1（4/4），使其具有樣本性。但如果數據集Zr≥25%，其中有較大比例的非真實的零，數據集的抗差性降低或不具有抗差性，零值可以作為“結構性零”適度隱匿，在Q2＞0或Q3＞0處左截斷，但不完全刪失，僅在Q3-Q1＞0處等效地觀察滿足異常值檢測的條件，保留一定比例的零值，使其具有等級結構性。因為零值并不是缺失值，在本研究中只是暫時未產生社會影響的觀測值，是一個隨時可能蘇醒的科學“睡美人”，它的存在有計量意義，將所有的零值刪失或隱匿會導致信息嚴重丟失。因此，依據不同數據集的零值長度即Zr，在滿足Q3-Q1＞0的條件下，均勻性縮減數據集的零值，既可以保證每個數據集的異常值檢測的一致性和抗差性，也可以保留數據集之間的原始信息差異，同時可以觀察數據集左側齊性和右側異質性對異常值的影響。由于四分位Zr≥75%，異常值無法檢測，因此，高零值條件下Zr的縮減率≥0.25是四分位異常值識別的充要條件。

異常值識別前數據集左側的抗差性處理，可以采用滿足一致性控制要求的四分位零值率（Qr）進行自適應零調整。其中，零值率的分位數定義為Q1、Q2、Q3、Q4四個分位；零值的分位保留系數定義為四個等級結構：1（4/4）、3/4、1/2（2/4）、1/4；四分位零值率定義為四個區間的分段控制函數及其縮減的值域。從以上定義及其三者之間的關系，可以推導出以下定理和引理。

定理2.在四分位數據集中，若Zr的分位越低，則Qr越低，Qr縮減的值域也越低；若Zr的分位越高，則Qr越高，Qr縮減的值域也越高。

引理1.Qr縮減的初始值域等于0，即Q2最小Zr與Q2下限的Qr之差等于0；Qr縮減的最大值域等于一個臨界值，即Q4最大Zr與Q4上限的Qr之差漸進于常數0.375。

顯然，四分位零值縮減法就是通過變量求Zr與Qr之差。依定理1，四分位零值率的分段控制函數為

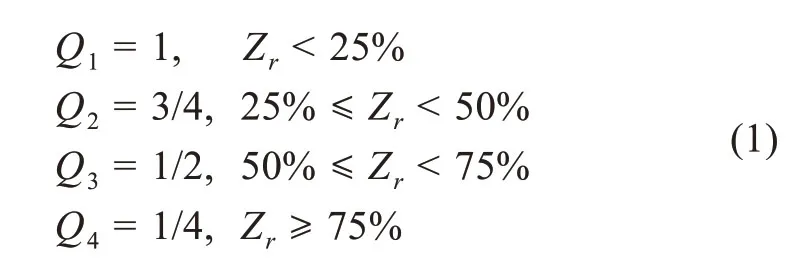
因為公式(1)中分段函數的斜率不一致，低分位上限和高分位下限的端點間等級下降速度不均勻，所以用端點空白值作線性回歸的Y軸截距，進行一致性逼近校正，依定理2，四分位零值率的精確計算公式為

公式(2)中，Qr縮減的最小值域等于0，最大值域漸進于常數0.375，引理1得證。

由于截距是等級下降速度的0.25/4或相應的倍率，用公式(2)計算，一致性準確率達到98.81%，回歸標準誤差為0.0207。公式(2)中，Qr在各分位區間段上單調遞增，在所有分位也單調遞增且連續，分段函數實現平滑銜接。

3.2 基于右側多異常值和極端右偏斜分布的穩健方法

計量評價研究的主要目的是多源信息評價，通常意義上也稱為多指標綜合評價。不管綜合評價或信息聚合采用何種方法，包括加權還是不加權、線性還是非線性、獎勵還是懲罰、標準化/無量綱化還是近似算子，都離不開均值、最大值等中間和右側數據的耐抗性和可靠性。因為來源數據一旦存在多異常值和極端右偏斜分布，必然會使均值、最大值、標準差等變量發生扭曲，從而對映射、標準化/無量綱化或算法的耐抗性和可靠性產生影響。

對線性比例的均值化法而言，信息計量學和統計學具有耐抗性和可靠性的方法主要有以下幾種。

（1）切尾均值（trimmed mean，TM）。假設X1≤X2≤…≤Xn樣本容量為n的順序觀測值，稱每側切除t個觀測值再計算剩余數據集的均值，為數據分布1-α中心部分的切尾均值[33]，

(5)實訓環節的設計：中職、高職院校非常重視實訓教學，克服困難到在建項目施工現場進行教學，但是由于交通問題、安全問題、在建項目選擇等問題，大部分課堂教學、實訓環節仍在校內完成。校內實訓基地建設時追求觀賞性、展示性，甚至試圖真實再現施工現場，不屑讓學生參與砌墻、抹灰、墻磚鑲貼等最基本的工作，實訓教學時流于形式，學生真正動手操作的環節不足，難以達到預期的效果。中職階段，應該重視學生的操作和動手能力，例如墻面磚鑲貼時，只通過視頻、幻燈片來展示其施工過程，學生只能掌握基本的工藝流程，如果讓學生動手完成墻磚鑲貼的全過程，這樣更能吸引學生的興趣。

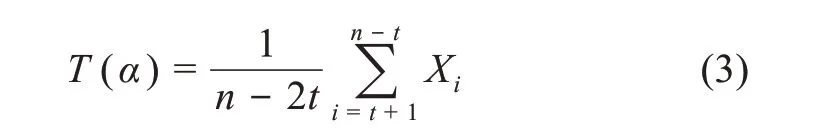
其中，α為切尾率，α=(t/n)×100%。

顯然，αn/2觀測值要從每側移除。特別地，當α=0%時，切尾均值就是均值；當α=50%時，即左右兩側各切除大約50%，僅保留中間順序觀測值（n為奇數時保留一個，n為偶數時保留兩個），將其余順序觀測值全部切除，切尾均值就是中值。由于α切尾均值的崩潰點是α/2，隨著區間α值的增加，α切尾均值的耐抗性和可靠性將更加穩健。當其崩潰點為0時，均值可以被一個孤立點扭曲，說明均值極不穩健。

切尾均值未丟棄數據集中間的大部分信息，能有效地抵抗或消除左右側異常值（或離群值）及局部偏斜的影響，從而更穩健地反映數據總體的平均水平。此外，若數據集是正態分布，則均值和切尾均值將是相同的。

（2）縮尾均值。縮尾均值是通過將異常值（或極值）替換為某些百分位的數據來確定的，這為所有統計分析提供了一個合理的集中趨勢表示[34]。它基于對數據進行排序，將最低α×100%和最高α×100%互變模擬值和觀測值，并將異常觀測值替換為邊界值X([αn])和X([(1-α)n])最接近的模擬值，根據試驗的極值分配權重。用方程式描述縮尾均值Wα為

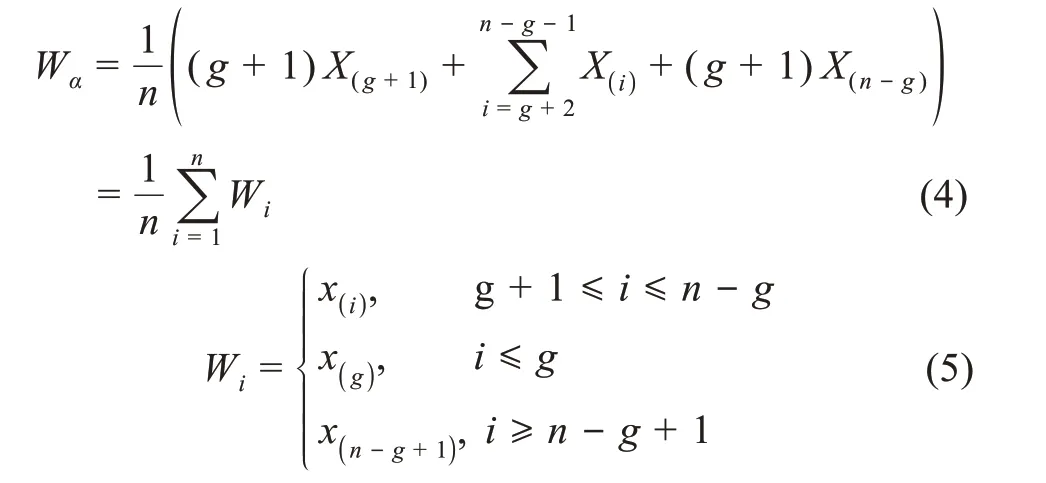
其中，g=[an]，g最大整數≤an，a表示最大允許估計誤差，n表示觀測數。

異常值的切尾或截斷的做法對耐抗性和可靠性是有幫助的，但會因集中在均值上而受到損害，導致樣本大小變化和邊界丟失。相反，像縮尾值這樣的穩健估計方法，可以用于縮尾修正，保留數據中心和兩側的重要信息。縮尾值修正估計量通常比未經篩選的估計量對異常值更具耐抗性和可靠性，因而，縮尾均值是樣本均值的一個很好的替代選擇。縮尾修正計量比切尾修正計量在技術上有更大的優勢：①用最接近異常值的位置替換或交換異常值；②數據的樣本大小保持不變；③有助于防止邊界信息丟失。

（3）MOM（modified one step M-estimator）和WMOM（winsorized modified one step M-estimator）。作為切尾均值和縮尾均值更好的替代品，推薦MOM（修正的一步M-估計量）和WMOM（縮尾修正的一步M-估計量），它可作為異常值出現時數據分布修正的估計量。

（4）縮序均值。它是一種基于縮序值的具有保留原始信息大小（序）關系的均值估計方法。多異常值的縮序計量方法與應用將另文研究。

4 網絡-替代計量指標數據的分類及其穩健計量方法

本研究的原始數據集來源于四川省2005—2014年的341項國家社科基金項目成果（專著類）的網絡-替代計量數據采集樣本，樣本總數683190件。其中，單一來源596269件（中國知網），精確匹配樣本事件數596261件，召回的精確率達到99.99%，采集數據的密度為2114.43件，強度為1748.59件；多源大數據86921件，精確匹配樣本事件數23121件，召回的精確率為26.60%，采集數據的密度為255.65件，強度為187.10件，表明指標數據具有一定的有效性和可靠性。具體的數據采集步驟、方法和結果見作者另文。

4.1 網絡-替代計量指標的分級-分類

由于越來越多的科學成果通過互聯網和社交媒體進行交流，用來評價其社會影響的網絡-替代指標也越來越多。根據國外學者和Altmetric.com、Plum Analytics等平臺應用[31-32,35-36]，社會影響評價的一級指標一般包括使用（usage）、引用（cita‐tion）、社交媒體（social media）、提及（mention）和獲取（capture）。其中，使用包括點擊、下載、瀏覽、圖書館藏書、視頻播放，引用包括引文索引、臨床引用、專利引用、政策引用等，社交媒體包括訪問量、點贊、分享、推文，提及包括博客帖子、評論、綜述、維基百科、新聞媒體，獲取包括書簽、交叉編碼、收藏、讀者數和觀眾數[36]。從理論角度看，網絡-替代計量指標的分級-分類涉及指標特征屬性的信息差異和相似性，如何區分或聚合面臨很大困難；從實際的操作角度看，沒有一個包容性的計量指標框架，網絡-替代計量會很困難。本研究基于社會影響指標的屬性重要性，以及組內和組間的相似、差異關系，數據位置和尺度的穩定性，同時考慮國內多源數據的易獲取性，將社會影響（相對于傳統的學術影響）維度的計量指標進行分級分類，具體分為兩級。一級指標共5個大類，分別是論文使用（C1）、專著獲取（C2）、網絡分享（C3）、網絡提及（C4）、社會應用（C5）。二級指標共18個小類，論文使用包括知網論文下載數；專著獲取包括圖書銷售、圖書館藏書，其中，圖書銷售又包括京東、當當、孔夫子銷售和讀者評分；網絡分享包括百度文庫、豆丁網、doc88、book118、博客；網絡提及包括搜索引擎采集到的精確匹配提及網頁；社會應用包括新聞、百科、評論、綜述，其中百科只包括知識百科，不包括人物百科。

4.2 極端異常值的常規識別與抗差性識別方法對比

首先，對5個一級指標按Ⅰ（表1）即零值完整保留，得到無任何縮減的數據集，簡稱無縮減集。依據四分位距（上四分位值與下四分位值之差即IQR=Q3-Q1）絕對值大于3倍四分位值的區間設定為極端異常值（extreme qutlier），即極端異常值依據

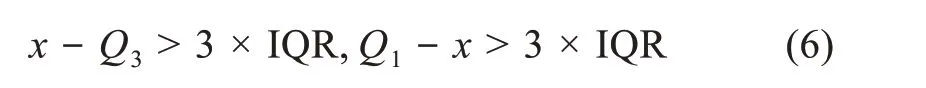
進行常規識別（或抗差性識別）。依據異常值識別的常規方法，數據集零值無縮減即全保留，得到常規識別異常點檢定結果，如表1（Ⅰ）所示。

其次，對2個零膨脹分布一級指標C2、C5，按照前述抗差性控制要求，對數據集Zr按公式(2)進行四分位自適應零調整，得到零值有限縮減的數據集，簡稱零值縮減集。代入公式(6)，依據異常值識別的抗差性方法，得抗差性識別異常點檢定結果，如表1（Ⅱ）所示。

同時，保留非零膨脹分布一級指標C1、C3、C4的常規識別異常點檢定結果，得到匯總數據（表1）。

表1 極端異常值的常規識別與抗差性識別結果

從表1可見，常規識別異常點有115個，抗差性識別異常點有44個，其中指標C2、C5的異常點識別結果差異最大，為此，采用箱線圖進行直觀對比。

從圖1的C2無縮減集可見，由于受高零值和零膨脹的影響，C2的常規識別中，異常點的圖框中線和頂部都已接近零，極端異常點達到68個，而C2的非零值數據總共才93個，可見常規異常值識別不具有抗差性。相反，從圖1的C2零值縮減集可見，在采用公式(2)進行四分位自適應零調整、縮減111個結構性零后，C2的抗差性識別中，異常點的圖框頂部已得到明顯提升，指標C2的極端異常點降到11個，異常值識別和檢定的抗差性大大提高。類似情況在指標C5中也有充分體現。由此可見，四分位零值縮減法處理對于零膨脹下極端異常值的識別，具有很強的適切性和抗差性，是異常值合理修正及其穩健計量的重要基礎。

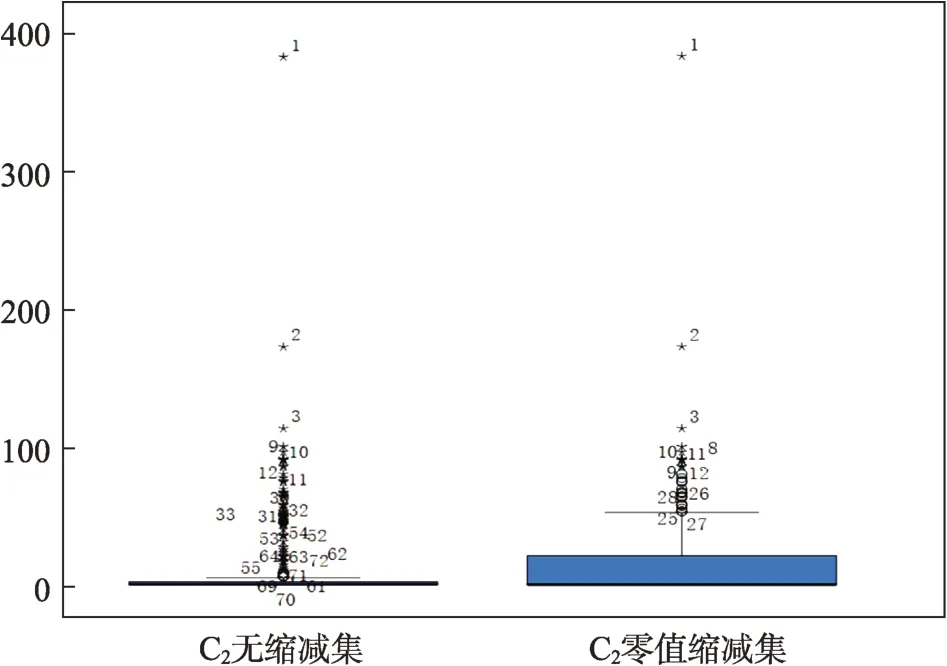
圖1 C2無縮減集與零值縮減集的箱線圖對比

4.3 極端異常值的縮尾求穩修正方法

對于檢定后的表1極端異常值，可采用縮尾求穩和縮序求穩兩種方法修正。縮尾求穩修正應用縮尾值公式(4)和公式(5)，將極端異常值替換為最接近極端異常值的值即中度異常值的最大值，模擬條件下則將異常值替換為邊界值X([αn])和X([(1-α)n])最接近的模擬值，方法相對成熟和簡單。縮序求穩修正將另文研究。

按照以上縮尾求穩方法和縮尾值計量結果，重新計算5個一級指標數據集的主要統計量和統計參數，得到表2。

從表2可見，極端異常值較多的C3、C2、C1最大值顯著降低，縮尾求穩修正后的數據集（修正值即縮尾值）降低了原始觀測值的數量級，在一定程度上實現了異常值的降維、降權和一致性，為下一步的無量綱化和多指標綜合評價結果提供了良好基礎。顯然，修正后的數據集在最大值、均值、標準差和方差等方面，都比修正前的數據集更具耐抗性和可靠性，數據集的極端右偏斜分布偏差和誤差得到有效抵抗和削弱。

表2 縮尾求穩修正前后的主要統計量和參數

5 穩健計量在國家社科基金評價中的應用

網絡-替代計量數據的異常值識別和修正，極大地提高了原始數據集的合理性和穩定性，但在綜合評價的穩健性上仍然面臨兩大問題：一是指標數據的量綱和量級不同，如何進行穩健性的無量綱化和計量；二是各項指標的重要性和數據信息不同，如何進行穩健性的權重系數求解和綜合評價。

5.1 穩健性無量綱化的方法選取及其應用

指標數據的無量綱化處理有線性無量綱化和非線性無量綱化兩種，前者能保留原始數據集的分布形態，后者則會改變原始數據集的分布形態。本研究對44個極端異常值的識別和合理修正，可以看作一種極大型區間的線性預處理，是穩健計量評價的重要基礎。線性無量綱化具有保留原始數據分布特征和簡單實用的優點，且極端異常值對線性無量綱化的干擾已經排除，因此本研究不再考慮非線性無量綱化。

線性無量綱化處理的方法主要有標準化法、歸一化法、極值法、線性比例法、功效系數法和向量規范法等；其中線性比例法的比例系數可取最大值、最小值、均值等，分別稱為最大值法、最小值法、均值化法。這些方法之所以不同，是因為采用不同的特殊值和線性函數進行一致性映射與轉換，因此產生不同的評價值和綜合評價結果。

在標準化法、Z-Score法和特殊值取均值、總和、平方和的線性比例法中，由于特殊值和線性函數中包含樣本整體信息的統計量，一致性和穩定性都較好。其中，標準化法、Z-Score法會使組內方差和變異系數發生巨大改變，說明組內信息受損嚴重，一致性差；極值法、最大值法、最小值法和功效系數法，由于特殊值和線性函數中值只包含樣本信息的個別特殊統計量（如最大值、最小值等），容易受到極端數據分布的影響，且不能明顯縮小各指標間數量級差異，穩定性和一致性都較差。

在常用的無量綱化方法中，作為線性比例方法的均值化法，由于受極端值的影響相對較小，能縮小各指標間數量級差異并顯現原始數據集的差異信息，且變異系數不變，主要統計量和參數的穩定性、一致性都較好。此外，均值化法在基于序關系分析法（G1法）的綜合評價應用中，還能使指標權重對評價值的影響實現一致性和穩定性。因此，從無量綱化方法選取和一致性轉換的諸多因素綜合考慮，基于均值的線性比例法都是一種比較理想的穩健性無量綱化方法。

由于均值化法易受樣本值，特別是極端值的影響[37]，基于穩健性要求，可采用基于縮尾求穩或縮序求穩的方法對原始數據集的異常值進行修正，本研究采用前者。

修正后的數據集，因采用縮尾值代替原始值中的極端異常值，消除了異常值對樣本值的影響，使均值化轉換的特殊值（縮尾均值）更能顯現差異信息。均值化法計算公式為

其均值化法處理后的主要統計量和參數如表3所示。

從表3及與表2的對照可以看出，采用基于縮尾均值的線性比例方法處理后，各指標間縮尾值（修正值）的數量（級）差異，與原始值相比得到有效縮小，因此數據集的極端右偏斜分布得到改善，極端異常值較多的C3、C2、C1最大值顯著降低；指標重要性高的C5，方差分量提高幅度最大，最大值為5個指標中最高；最大值和方差都在較小差異的同一值域范圍內，且基本反映了各指標間的重要性，原始數據集的信息差異得到顯現。基于縮尾均值的線性比例方法轉換，因信息變異受損較低而更加穩定和一致。

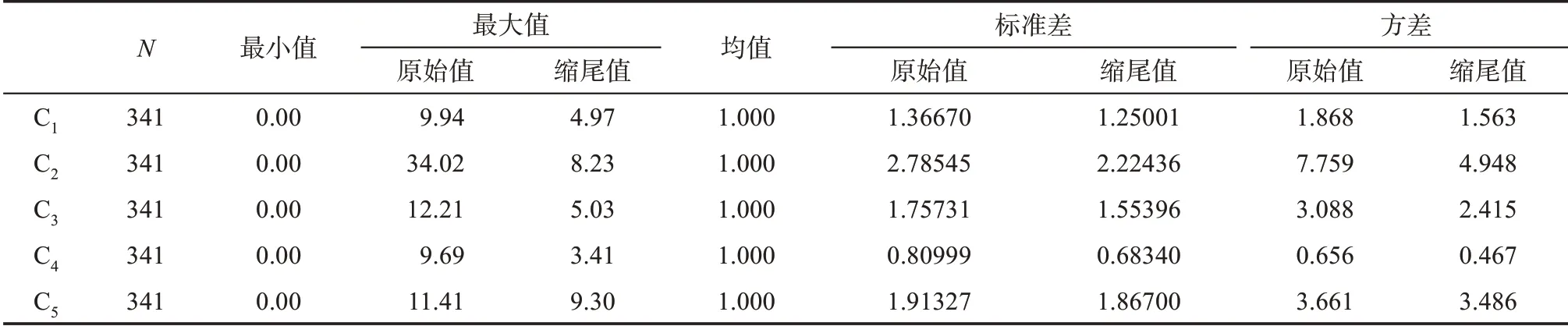
表3 均值化法處理后的主要統計量和參數（基于原始值和縮尾值）

5.2 穩健性權重求解及方法選取

指標屬性的重要性和主觀權重求解，如何反映客觀的計量信息，使權重求解及其實現機制更具可靠性和可信度，是穩健計量評價需要考慮的另一個重要問題。

多指標綜合評價是一種基于原始值（修正值）計量、特殊值轉換和評價值綜合或聚合的價值測度體系，其價值測度的實現主要有四種途徑：一是基于計量對象的客觀賦權法，代表方法有熵權法、DEA（data envelopment analysis）法、標準差法、變異系數法，能反映數據樣本的相關性和信息量，但缺乏評價方法和結果的一致性和穩定性，方法不同導致結果也不同；二是基于評價主體判斷的主觀賦權法，代表方法有AHP（analytic hierarchy process）法、Delphi法、G1法，能反映指標本身的重要性程度和專家群體的知識，但缺乏評價前提和過程的可靠性和可信度，權重賦值與計量數據無關；三是基于對象和主體的主客觀賦權法，也稱為組合賦權法，代表方法有平均值法、Borda法、Copeland法、最小二乘法、離差最大化法，能綜合反映主客觀判斷，但缺乏方法和評價體系的一致性，體系和評價方法存在沖突或“硬性”；四是基于多種數學模型的合成優化法，代表方法有非線性優化法、線性優化法，能不區分主客觀差異融合多種評價方法，但缺乏評價方法和結果的適切性，評價目標或準則依賴主觀判斷[38]。

盡管不同的權重求解方法有不同的實現機制，但基于一種主觀權重求解同時又完全融入一種客觀權重求解，可以構造出一種同時具有主觀可靠性和客觀可信度的新方法。本研究選取的G1法應用，有機融入客觀賦權法（標準差法），使其兼具兩種方法的優點，克服各自的不完備和非穩定性局限。

5.3 穩健G1法及其權重系數求解應用

穩健G1法是一種在主觀賦權法中融入客觀賦權法，將專家群體的理性判斷和樣本數據的客觀信息量有機結合的權重求解方法。權重主觀可靠性和客觀可信度的優勢互補，使權重值具有主觀-客觀雙實現機制，從而提高綜合評價結果的可靠性和穩定性。

G1法也稱為序關系分析法，是一種傳統的主觀權重求解方法[39]。權重系數求解基于國家社科基金成果社會影響指標的序關系分析，有10位咨詢專家參與，通過調查問卷評分方式，得到5個指標的重要性程度及其rk賦值信息。專家根據自己的經驗和偏好，對5個指標的重要性程度，按從強到弱順序確立序關系，并對5個指標的重要性標度ωk-1/ωk進行理性判斷。

若在m個評價指標中，專家給出兩個指標之間的重要性程度之比為rk，則權重系數的求解公式為

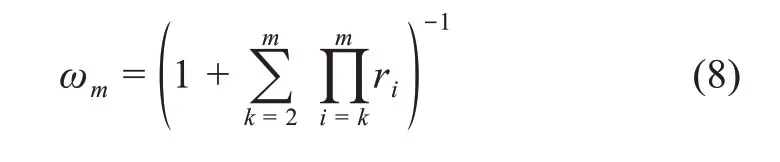
專家建立的序關系和相對重要程度rk賦值以及G1法權重系數求解結果如表4所示。

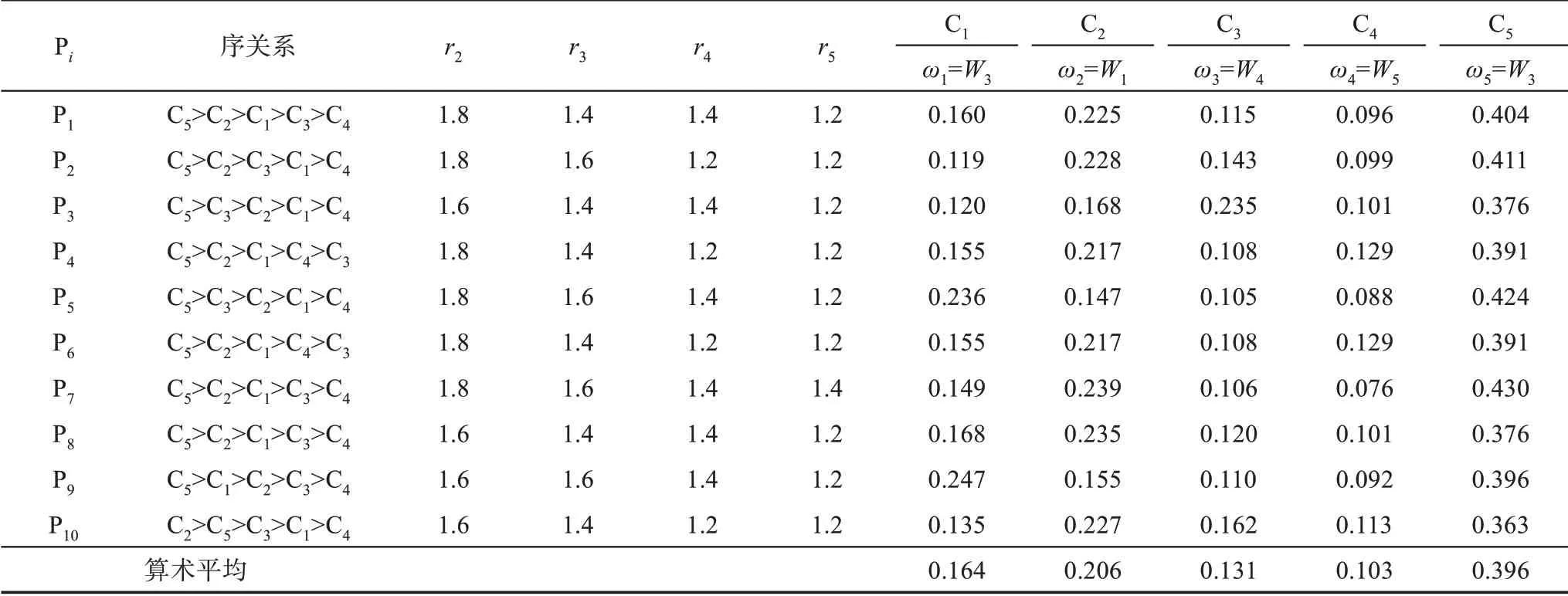
表4 G1法序關系、rk賦值及其權重系數求解結果

從表4可見，不同的專家有不同的序關系判斷及其rk賦值和權重系數。通過G1法10位專家群體權重系數的算數平均，得到指標C1、C2、C3、C4、C5的群體權重系數，分別為0.164、0.206、0.131、0.102、0.396，即群體確立的最終序關系為C5＞C2＞C1＞C3＞C4。

在傳統的主觀賦權法中，G1法采用專家群體的知識判斷，評價方法和結果具有很強的一致性和穩定性；但由于不能反映數據樣本的相關性和信息量，評價前提和過程缺乏客觀可靠性和可信度。依據李剛等[40-41]提出的標準差修正G1組合賦權及其合理性研究，以及易平濤等[42]提出的一種取代傳統主觀序關系的客觀序關系分析法，本研究構造出基于標準差的客觀G1法和半客觀G1法，并與G1法有機融合，最終形成穩健G1法。

客觀G1法的序關系建立，不是直接采用專家群的知識判斷，而是根據樣本數據中的信息量即相鄰指標標準差的大小（見表3），重新確定序關系及相對重要性程度rk賦值，并通過公式(8)求解權重系數。根據表3，原始值的標準差序關系為C2＞C5＞C3＞C1＞C4，rk賦值分別為1.69、1.46、1.28、1.09。將rk賦值代入公式(8)，得到基于原始值的客觀G1法C1、C2、C3、C4、C5的權重系數值，分別為0.121、0.384、0.156、0.112、0.227。同理，根據表3，可得到基于縮尾值（修正值）標準差序關系及rk賦值，分別為1.83、1.24、1.20、1.19，代入公式(8)得到相應指標權重系數值，分別為0.138、0.376、0.165、0.116、0.205。

半客觀G1法是利用G1法專家群體確立的序關系，計算C5＞C2＞C1＞C3＞C4相鄰指標的σk-1/σk之比作為rk賦值，再根據表3原始值（或縮尾值）的標準差序關系，代入公式(8)。同時，對rk進行如下限定：

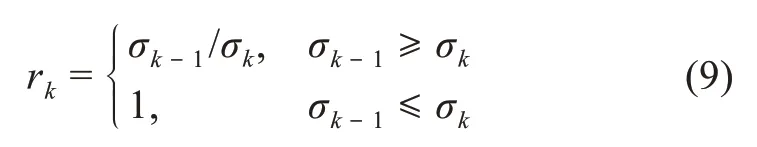
得到基于原始值標準差序關系修正后的rk賦值，分別為2.17、2.04、1.00、1.00，通過公式(9)并參照表4，重新計算基于原始值的半客觀G1法C1、C2、C3、C4、C5的權重系數值，分別為0.106、0.215、0.106、0.106、0.467。同理，根據表3的縮尾值，通過公式(9)并參照表4，可得到基于縮尾值標準差序關系修正后的rk賦值，分別為2.27、1.78、1.00、1.00，相應指標權重系數值分別為0.113、0.202、0.113、0.113、0.459。

將以上權重系數求解結果匯總，得到表5。

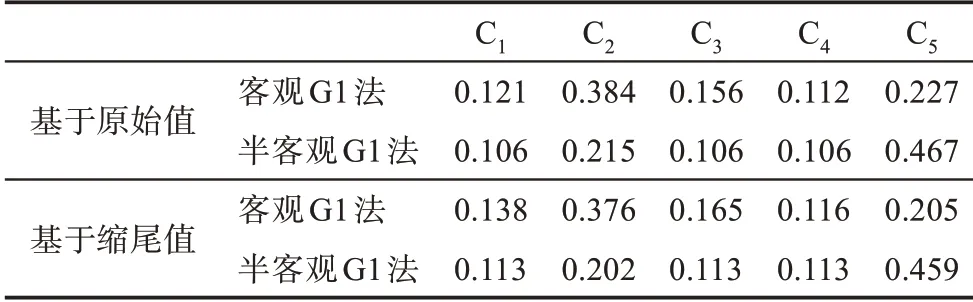
表5 客觀G1法、半客觀G1法權重系數求解結果

基于權重系數求解的主觀-客觀雙實現機制要求，將表4中的G1法權重集和表5中的客觀G1法、半客觀G1法權重集，看成一個三角模糊數，進行去模糊化處理，轉化為精確值，得到穩健G1法的最終權重系數修正值。具體計算依據梯形重心法公式

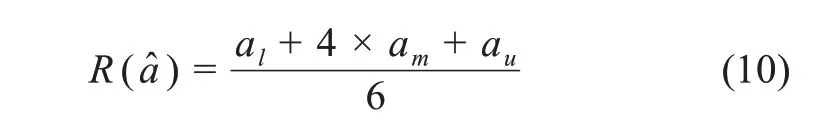
將表4和表5的3種G1法的權重系數代入公式(10)，得到基于原始值的穩健G1法C1、C2、C3、C4、C5的權重系數修正值，分別為0.147、0.237、0.131、0.105、0.380；基于縮尾值的穩健G1法C1、C2、C3、C4、C5的權重系數修正值分別為0.151、0.233、0.134、0.107、0.375。以上最終權重值的序關系與G1法一致，因此，穩健G1法實現了具有客觀可信度的樣本信息量，與具有主觀可靠性的專家群知識的有機融合。

5.4 穩健性方法在國家社科基金成果評價中的具體應用及結果

在國家社科基金成果的社會影響評價應用中，穩健性計量評價有以下重要步驟。

（1）極端異常值的檢定和計量處理。基于抗差性控制要求進行異常值識別，將原始值（數據集）的極端異常值修正為穩健性的縮尾值。

（2）無量綱化處理。對于修正后的數據集，應用基于縮尾均值的線性比例方法，得到更具穩定性的無量綱化值；為了對比，同時也對修正前基于均值的指標值進行無量綱化處理。

（3）指標權重系數的穩健G1法求解。基于專家群體知識，以及客觀和半客觀序關系（標準差）信息，得到具有主觀-客觀雙實現機制的權重系數。穩健G1法的標準差來自修正后的數據集，非穩健G1法的標準差來自原始數據集。

（4）基于以上處理和求解計算綜合評價值，得到具有穩健性或非穩健性的綜合評價結果。

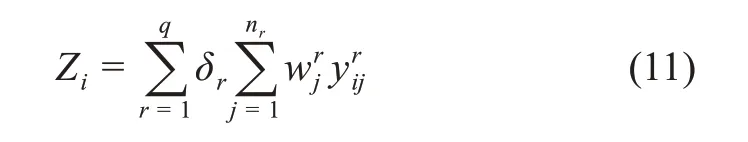
對于國家社科基金項目成果的社會影響評價來說，綜合評價值越大，則社會影響越大。

為了與穩健方法進行對比分析，本研究同時也基于原始值（完全保留極端異常值）進行非穩健的無量綱化、權重系數求解和綜合評價，其方法、步驟與基于縮尾值（修正值）的穩健方法一致。基于縮尾值的穩健綜合評價和基于原始值的非穩健綜合評價結果及其排序對比如表6所示。

從表6可見，基于縮尾值的綜合評價排序和基于原始值的綜合評價排序差距較大，在前10%排序中，最大秩距33位；其中，成果《主體功能區人口再分布實現機理與政策研究》如果基于縮尾值，排序第34位，但如果基于原始值，即完全保留極端異常值，則排序第1位。也就是說，在本研究341個對象的排序中，社會影響排名第1位的科研成果因為一個極端異常值，最終結果可以從第34位躍升至第1位；但如果基于縮尾值即穩健的綜合評價排序，這項成果就只能從第1位跌落至第34位。由此可見，基于穩健方法的計量和評價，對于綜合評價的真實性和合理性具有極其重要的影響和作用。此外，從有異常值的指標個數看，在社會影響排名前10%的科研成果中，有13項成果有極端異常值，占比達到38%；其中，有2個及以上極端異常值的成果2個。非穩健計量評價對綜合評價的真實性和合理性可能產生重大的偏差和影響，因此，基于穩健方法的計量評價具有重要的理論意義和應用價值。

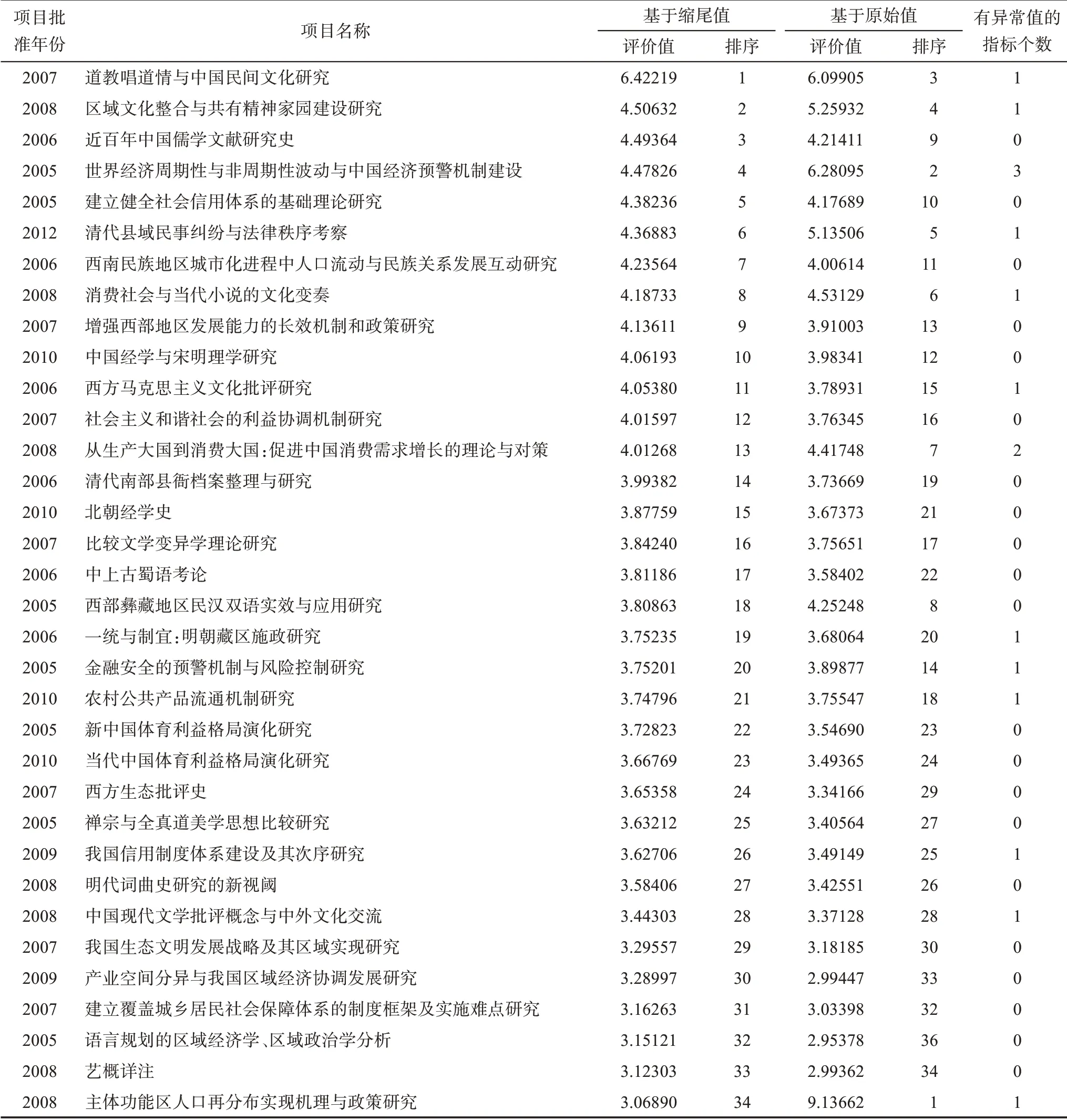
表6 穩健和非穩健綜合評價計算結果及其排序

此外，表6還對34項成果的批準年份進行了統計，可初步觀察指標值和時間因素之間的相互影響。在社會影響最大的34項成果（前10%）中，有30項 是 前5年（2005—2009年）的 成 果，占 比88.24%，只有4項是后5年（2010—2014年）的成果，占比11.76%，說明成果時間越早影響越大；盡管有些指標數據在早年的網絡平臺上量值不高或沒有，但因排序前34項成果的單指標數據覆蓋率都達到100%（無零值），這部分成果受影響不大。因此，應重點關注計量評價的時間累積效應，建立一種更精確的基于時序動態響應的穩健計量評價方法。

6 結論及建議

傳統計量評價對網絡環境下科學成果的社會影響及其數據集的不確定和不完備局限或缺陷并不十分清楚。本研究基于網絡-替代計量下高零值、多異常值和極端右偏斜分布的復雜挑戰及其機理分析，通過四分位零值縮減法、異常值縮尾求穩法，以及權重系數穩健G1法等方法創新，探討數據集的真實性、合理性及其計量評價的抗差性、可靠性和穩定性與社會影響評價之間的復雜聯系和科學出路，得出以下結論及建議。

（1）對于左側高零值和零膨脹分布挑戰，零值的全截斷不但會使樣本結構嚴重丟失，而且會導致右側異常點的檢測結果大大降低；但如果零值全保留，又會因零膨脹導致右側異常點大大增加，Zr≥75%異常值甚至無法檢測。由于數據集存在多異常值，計數模型中基于零膨脹的總體混合概率必然受到影響，其真實的或過度的零值擬合數據也不可靠。相反，計量模型中基于Qr控制函數的縮減法，則可以完全避開計數模型中的多異常值影響，能比較好地解決零膨脹及其異常值檢定的抗差性問題，在既不全截斷也不全保留中找到一個危險率較低的理想點。

因為四分位異常值識別的基本假設是基于四分位距的穩健性，將Q4和Q1截斷，且Q3-Q1＞0，以中間分位的尺度參數作為樣本的總體估計。Zr≥75%時，Q3=Q1=0，Zr的縮減率必須大于0.25，即Zr-Qr＞0.25，這既是異常值檢定的充要條件，也是異常值檢定的“必要變異度”。因此，在零調整的縮減率漸進于0.375時，由于Zr≥75%，Qr縮減的值域危險率應該扣除0.25的“必要變異度”；扣減后的縮減率才是實際危險率，它的最大值為0.125。而0.125正好是一個分位的中位數，對于三個分位的支撐集而言，屬于危險率較低的理想位置參數估計點。這就說明，即使Qr縮減的最大值域為臨界值0.375，它的實際危險率仍處于0.125的較低水平。

由于四分位零值率是從具有穩健性的四分位距法進行定義和推導的，且符合高零值樣本置信區間理論和零膨脹樣本結構理論及其方法，以及Brookes提出的“解釋信息計量分布的長尾必需用等級”的方法[27]，Cronin提出的替代計量學的“必要變異度定律”（law of requisite variety）[43]，因而對于高零值條件下的異常值自動檢測和識別，四分位零值縮減法具有很強的適切性。經過一致性逼近校正后，四分位零值率及其精確計算公式還具有很好的一致性和抗差性，是異常值合理修正及其穩健計量的重要基礎。未來在信息計量學、評價學和統計學及其相關學科中，這種四分位自適應零調整方法可以得到更廣泛的應用。

（2）對于數據集右側的多異常值和極端右偏斜分布挑戰，釆用基于縮尾均值的縮尾求穩方法處理，不但能消除極端異常值的影響，而且還能使數據的樣本大小保持不變，防止總體信息丟失，使右側數據在一定程度上實現降維和降權。

權重系數求解基于主觀賦權法，有機融入客觀賦權法，構造出一種具有客觀可信度的樣本信息量，與具有主觀可靠性的專家群知識有機融合的評價方法。通過梯形重心法公式，將G1法（主觀）和客觀G1法、半客觀G1法的權重集看成一個三角模糊數，進行去模糊化精確處理，得到穩健G1法的最終權重系數修正值，使權重值具有主觀-客觀雙實現機制，從而提高了綜合評價結果的可靠性和穩定性。

（3）應用研究表明，基于縮尾值的綜合評價排序和基于原始值的綜合評價排序差距較大。因此，科學成果的非穩健方法，對于綜合評價的真實性和合理性可能產生重大的偏差和影響，科學成果的穩健計量評價具有重要的理論意義和應用價值。

與非穩健計量評價方法的對比，穩健計量評價通過高零值下四分位零值率的抗差性檢定、多異常值下的縮尾求穩、極端右偏斜分布下基于縮尾均值的線性比例映射及其權重系數主客-客觀雙實現求解等方法的應用，使計量評價的穩定性、可靠性和抗差性都大大提高。

盡管科學成果及其社會影響的計量評價面臨數據集左側、右側和極端向右偏斜分布之間的復雜關系及其由此帶來的諸多科學挑戰，特別是方法和結果的抗差性、可靠性和穩定性，但同時也帶來諸多科學機遇，有利于促進信息計量學、評價學及相關學科向復雜性精確科學方向發展。現在，即使是存在高零值和多異常值數據，即若有蓄意通過網絡-替代計量數據（如點擊率）來提升成果的社會影響，穩健性計量評價也有相當可靠和穩定的方法進行有效抵抗、削弱或消除。未來的發展方向，建議研究一種比基于必要變異度定律更復雜和精確的基于穩健變異度定律的縮序計量方法，以及一種基于時間累積的時序動態響應計量方法，以對數據普遍存在的計數為0及其他不規則性進行積極防御和高效抵抗。