指向高階思維的圓錐曲線解題教學(xué)
滕詩媛 (浙江省溫州市第八高級中學(xué) 325000)
圓錐曲線是高中數(shù)學(xué)知識中的重要內(nèi)容之一,也是高考的一個高頻考點(diǎn),往往出現(xiàn)在選擇或填空題的靠后位置和大題的倒數(shù)第二題,其難度和重要程度不言而喻.圓錐曲線主要考查學(xué)生的直觀想象、數(shù)學(xué)運(yùn)算和邏輯推理等核心素養(yǎng),難點(diǎn)在于計算量大和幾何條件代數(shù)化.

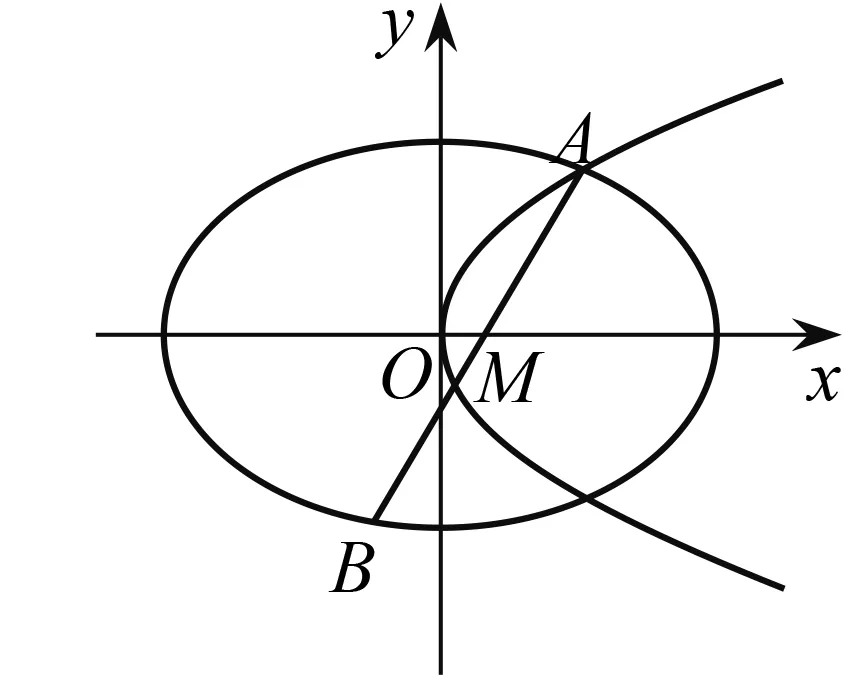
圖1
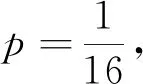
(2)若存在不過原點(diǎn)的直線l,使得M是線段AB的中點(diǎn),求p的最大值.
本題的第(1)題比較簡單,本文重點(diǎn)對第(2)題進(jìn)行研究.學(xué)生拿到題目按照以往的慣性思維進(jìn)行解題:設(shè)點(diǎn)A(線)、聯(lián)立(拋物線和橢圓方程)、建立目標(biāo)函數(shù)求最值[1].解題思路自然,但解法繁瑣,學(xué)生沒有足夠的時間將題目解完整,甚至沒辦法將目標(biāo)函數(shù)與已知條件聯(lián)系起來.究其原因是學(xué)生未能思考問題本質(zhì)進(jìn)而形成自己的解題策略,而教師也往往停留在常規(guī)解題方法進(jìn)行教學(xué),沒有分出時間與精力處理學(xué)生這一個性化問題.
布魯姆教育目標(biāo)分類原理將認(rèn)知過程分為記憶、理解、應(yīng)用、分析、評價、創(chuàng)造六個維度[2].以 本題而言,考查的是學(xué)生邏輯思維能力(即能正確領(lǐng)會題意,明確解題目標(biāo),能尋找到實(shí)現(xiàn)解題目標(biāo)的方向和合適的解題方法,對應(yīng)應(yīng)用與分析目標(biāo)),運(yùn)算求解能力(即能根據(jù)法則、公式進(jìn)行正確運(yùn)算變形,根據(jù)問題的條件和目標(biāo),尋找多種途徑,設(shè)計較為適合的方法進(jìn)行運(yùn)算、變形,對應(yīng)應(yīng)用與評價目標(biāo))和綜合應(yīng)用能力(即能對具體問題陳述的材料用數(shù)學(xué)語言正確地表述,用所學(xué)的數(shù)學(xué)知識、思想和方法解決問題,對應(yīng)分析、評價以及創(chuàng)造目標(biāo)).對照布魯姆六大認(rèn)知能力,這道題乃至這類題目的解題思維顯然屬于后三種的高階思維.在此類題目的解析過程中,幾何條件與代數(shù)表達(dá)進(jìn)行互化無疑是引導(dǎo)學(xué)生形成高階思維的能力載體,因此如何引導(dǎo)學(xué)生利用已有幾何性質(zhì)來分析與比較解題方法并將計算簡化、將幾何條件與代數(shù)表達(dá)進(jìn)行互化成了教師必須研究的問題.
1 溯本清源,理清學(xué)生思維癥結(jié)
筆者根據(jù)布魯姆六大認(rèn)知目標(biāo),對本題進(jìn)行能力知識二維目標(biāo)的編碼分析,形成了問卷,試圖通過學(xué)生答題結(jié)果與問卷調(diào)查的對應(yīng)分析,找出學(xué)生“卡脖子”的具體原因,進(jìn)而提出對應(yīng)的解決方案.
問卷的問題大致設(shè)置如下:
1.本次考試你的得分為分.
2.第21題你的得分為分.
3.第(1)題若未得滿分,你失分的原因是( ).
A.拋物線定義忘記了B.計算出錯
C.其他
4.為了建立目標(biāo)函數(shù),第(2)題你選取的自變量是( ).
A.k(直線l的斜率)B.點(diǎn)A坐標(biāo)
C.m(直線x=my+t) D.其他
5.第(2)題若未得滿分,你失分的原因是( ).
A.設(shè)出直線方程,與橢圓聯(lián)立后不知道該怎么做
B.用韋達(dá)定理得到點(diǎn)M,B坐標(biāo)后,算不下去了
C.運(yùn)算過程出錯,導(dǎo)致后面做不下去
D.想利用拋物線方程把點(diǎn)M和A坐標(biāo)表示出來,有思路,不會算
E.想利用M是中點(diǎn),用點(diǎn)差法轉(zhuǎn)化為斜率問題,沒算出答案
F.無從入手
G.其他
6.在解決這道題的過程中,你認(rèn)為自己還存在哪些問題( ).
A.橢圓拋物線的幾何性質(zhì)不熟練
B.運(yùn)算能力不強(qiáng)
C.自變量選取和目標(biāo)函數(shù)的判斷
D.動拋物線問題識別不出來
E.解題時,不會比較方法優(yōu)劣
F.其他
問卷的第1題和第2題統(tǒng)計學(xué)生整卷和第21題的得分情況,區(qū)分學(xué)生水平層次,結(jié)合問卷的問題設(shè)置,將不同水平學(xué)生的失分原因進(jìn)行區(qū)分.學(xué)生水平與得分情況成正相關(guān),整卷得分在80分以下的學(xué)生第21題的第(2)題得分很低,這部分學(xué)生基本屬于事實(shí)性知識和概念性知識沒有掌握,比如忘記拋物線性質(zhì),中點(diǎn)條件用不起來,是記憶、理解問題.
參照布魯姆六大認(rèn)知目標(biāo),分解學(xué)生答題過程,問題3~6羅列了學(xué)生可能出現(xiàn)的錯誤、可能會用的解題方法以及存在的問題,試圖對照錯因與解題方法找出學(xué)生在程序性知識和元認(rèn)知知識上存在的問題.統(tǒng)計學(xué)生第(2)題失分原因,如 表1所示.
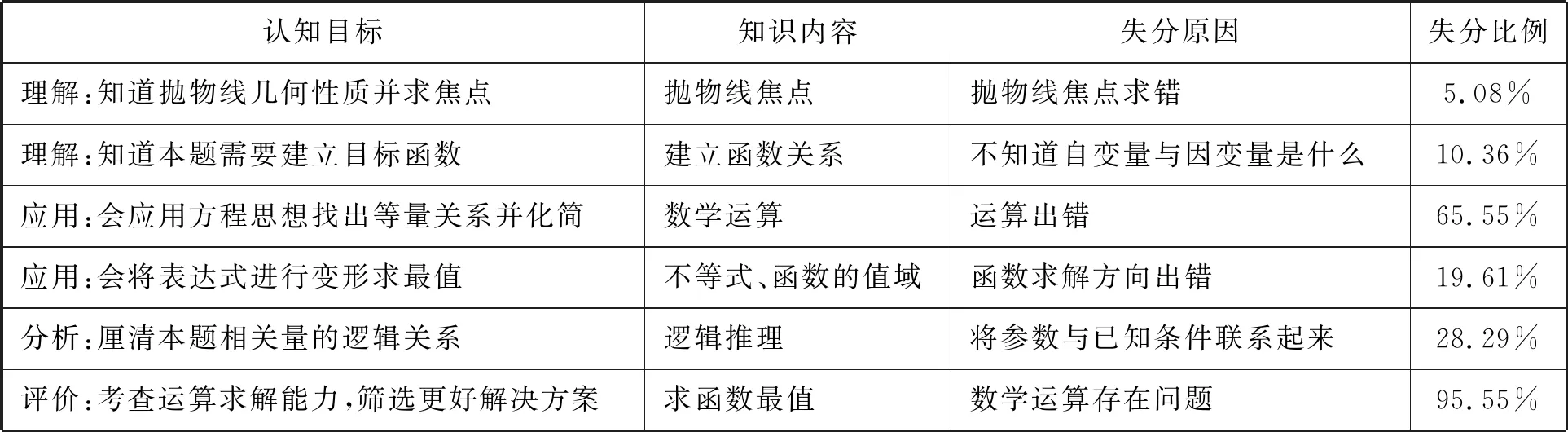
表1 布魯姆認(rèn)知目標(biāo)下學(xué)生解題失分原因分析表
由表1可知,大部分學(xué)生在事實(shí)性知識和概念性知識的應(yīng)用上已經(jīng)熟練掌握,也都清楚解析幾何解答題的變量最值問題的常用方法,但對于方法的選取以及數(shù)學(xué)運(yùn)算等程序性知識和元認(rèn)知知識的問題又顯得無從下手.多數(shù)學(xué)生失分點(diǎn)集中在選取合適的變量與方法進(jìn)行求解,將方程、函數(shù)、不等式進(jìn)行轉(zhuǎn)換,對應(yīng)認(rèn)知目標(biāo)屬于分析、評價過程出現(xiàn)問題.因此課堂教學(xué)的目標(biāo)應(yīng)聚焦于審清題目要求,以及為了解決問題如何引導(dǎo)學(xué)生整理思路,找到數(shù)學(xué)方法簡化數(shù)學(xué)運(yùn)算進(jìn)而完成解答上.
通過以上問卷調(diào)查的數(shù)據(jù)分析,從低階到高階,學(xué)生的失分率越來越高,說明本題“卡脖子”的原因在于學(xué)生的高階思維存在不足.
2 策略引導(dǎo),變換技巧尋求突破
上題考查橢圓、拋物線的簡單幾何性質(zhì),直線與橢圓、拋物線的位置關(guān)系,線段的中點(diǎn),這些知識點(diǎn)對高三學(xué)生來說都很熟悉,但大部分學(xué)生卻做不出來,其原因在于缺乏對解決問題的路徑進(jìn)行規(guī)劃,在變量的選取、方法的選擇等問題上仍有欠缺,關(guān)鍵問題在于數(shù)學(xué)運(yùn)算素養(yǎng)亟待提高.
數(shù)學(xué)運(yùn)算是指在明晰運(yùn)算對象的基礎(chǔ)上,依據(jù)運(yùn)算法則解決數(shù)學(xué)問題的素養(yǎng).主要包括:理解運(yùn)算對象,掌握運(yùn)算法則,探究運(yùn)算思路,選擇運(yùn)算方法,設(shè)計運(yùn)算程序,求得運(yùn)算結(jié)果.在解析幾何問題中,運(yùn)算素養(yǎng)主要體現(xiàn)在變量的選擇、條件的代數(shù)解讀、問題的代數(shù)解析.
常規(guī)做法很多時候不是最好的方法,在高考時間緊、難度大的背景下,若能對這一類題形成解題策略,學(xué)生便能提高得分率,更重要的是能引導(dǎo)學(xué)生從解題技巧的提高走向解題策略的提煉,成為以高階目標(biāo)驅(qū)動技巧方法、提升思維能力的教學(xué).為了引出仿射變換,尋求橢圓與圓之間的聯(lián)系,給出一道聯(lián)考試題進(jìn)行變式:
對以上變式,常規(guī)解題路徑包括運(yùn)用中點(diǎn)弦、聯(lián)立方程用韋達(dá)定理、刻畫三角形面積等,思路清晰計算量卻巨大.引導(dǎo)學(xué)生思考:是否還有其他方法?
橢圓可以看成是圓保持橫坐標(biāo)不變、縱坐標(biāo)壓縮后得到的圖形.圓有很多很好的性質(zhì),若能夠得到橢圓與圓之間的變換關(guān)系(即壓縮比),解題就會簡化很多.解法如下:
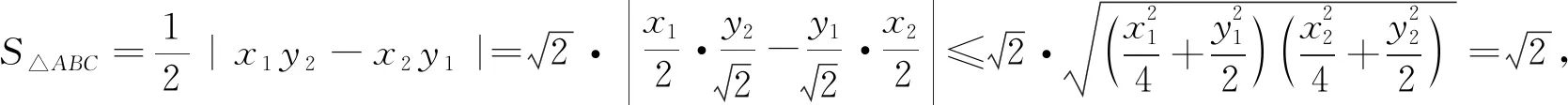
3 目標(biāo)高階,驅(qū)動性問題促進(jìn)教學(xué)
一題多解在高中數(shù)學(xué)解題技巧中很常見,簡化運(yùn)算的本質(zhì)是提高解題過程的思維含量,因此教師在教學(xué)過程中借助問題進(jìn)階將思維路徑可視化顯得尤為重要.
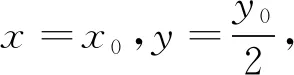
分析 課本上借助坐標(biāo)關(guān)系求解軌跡方程的推理過程,旨在尋求點(diǎn)M與點(diǎn)P坐標(biāo)之間的關(guān)系,以點(diǎn)P為中間量,得出點(diǎn)M橫縱坐標(biāo)之間的數(shù)量關(guān)系,這一過程揭示橢圓與圓的幾何與代數(shù)關(guān)系,將學(xué)生不太熟悉的橢圓問題轉(zhuǎn)化為圓的問題簡化運(yùn)算,將邏輯關(guān)系聚焦幾何問題坐標(biāo)化上,引導(dǎo)學(xué)生理解問題本質(zhì).
引導(dǎo)學(xué)生猜想:圓具有良好的幾何性質(zhì),如垂徑定理等,能否將橢圓變成圓,利用圓的有關(guān)性質(zhì)來輔助解決橢圓的相關(guān)問題?
為了更好地剖析問題,引發(fā)學(xué)生深度思考,對照布魯姆教學(xué)目標(biāo),設(shè)置以下幾個思考問題,如表2所示.

表2 認(rèn)知目標(biāo)與驅(qū)動性問題設(shè)置的對應(yīng)關(guān)系

- 中學(xué)數(shù)學(xué)雜志的其它文章
- 中國數(shù)學(xué)教育研究的現(xiàn)實(shí)圖景與未來道路
——聚焦國內(nèi)同行對ICME-14的學(xué)術(shù)貢獻(xiàn) - 基于數(shù)學(xué)運(yùn)算素養(yǎng)的一道聯(lián)考題的思考
- 探究構(gòu)圖 優(yōu)化路徑 提升素養(yǎng)
——記一道解析幾何題的求解歷程 - 追本溯源 深度思維
——對一道中考模擬壓軸題的思考 - “爬樓梯車輪支架旋轉(zhuǎn)半徑的優(yōu)化設(shè)計”辨析
- 高中數(shù)學(xué)跨學(xué)科教學(xué)的實(shí)踐
——以數(shù)學(xué)與人文學(xué)科的融合為例*

