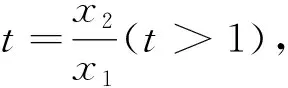極值點偏移問題的常見解法
——以2021年高考數學新高考I卷第22題為例
宗欣妍 (蘇州大學數學科學學院2019級基地班 215006)
極值點偏移問題以導數為背景,考查學生運用函數與方程、數形結合、轉化與化歸等思想解決問題的能力.此類問題呈現形式往往比較簡潔,涉及函數的雙零點,是多元函數問題.
1 極值點偏移的概念
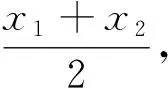

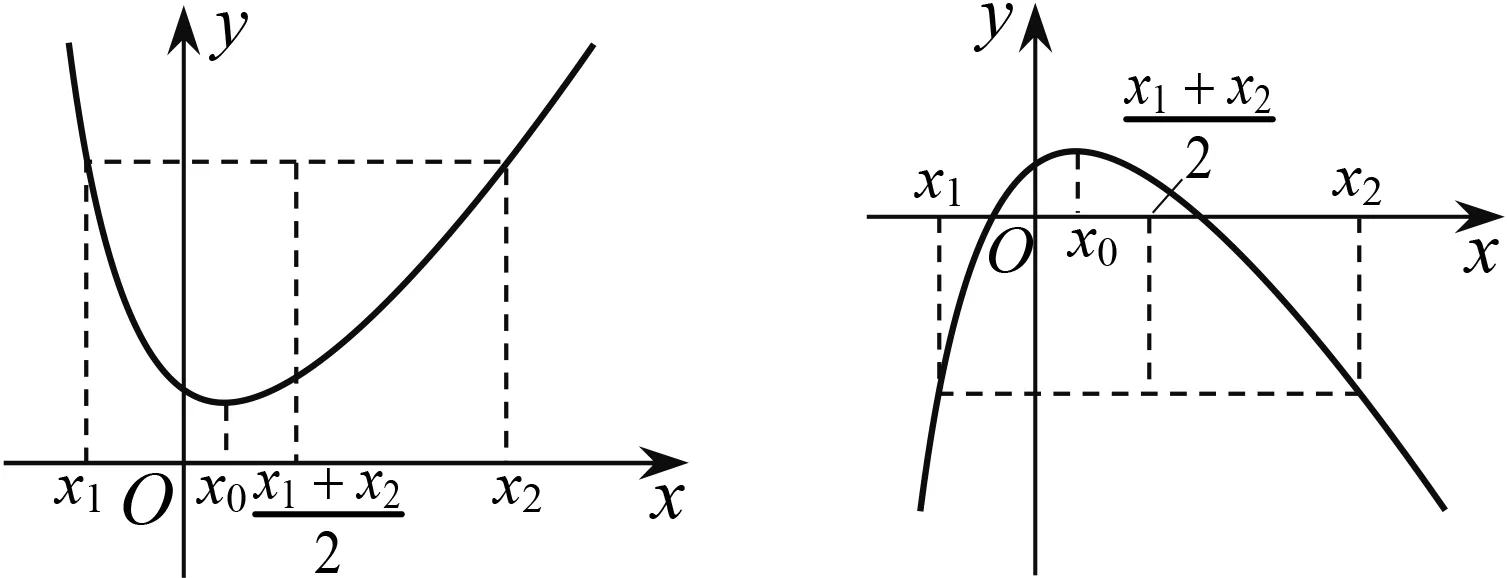
圖1 圖2


圖3 圖4
2 原題再現
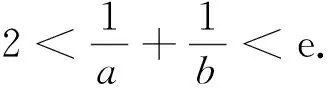
此題以基本初等函數為背景,主要考查了函數的單調性、利用導數證明不等式,考查了函數與方程、數形結合、轉化與化歸等思想方法,并突出考查了學生分析問題和解決問題的能力.
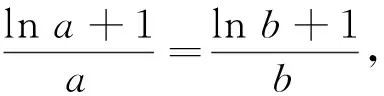
3 方法剖析
3.1 構造極值對稱差函數
函數f(x)的極值點為x0,若f(x1)=f(x2),要證x1+x2>2x0(或x1+x2<2x0),往往構造對稱差函數F(x)=f(x)-f(2x0-x)(x 點評構造對稱差函數是極值點偏移問題的一種通性解法,主要用來解決兩數和或者積與極值點相關的不等式證明問題.本題求證的不等式中含有兩個變量,對于此類問題一般的求解思路是將兩個變量分到不等式的兩側,然后根據函數的單調性,通過兩個變量之間的關系“減元”,建立新函數,最終將問題轉化為函數的單調性來求解. 事實上,有關極值點偏移的問題在高中階段大多與指對數函數相關,而雙變量的不等關系自然也可以捆綁借助對數平均不等式鏈來解決. 這里要說明的是,對數不等式在考場上并不能直接使用,用必證之(證明見文[1]). 點評應用對數平均不等式鏈來證明雙變量不等式,思路簡捷、別具新意、易于理解和掌握,在證明解答題時要“先證后用”.對數平均不等式的運用是近幾年數學競賽、高考數學命題的理論背景,它包含多個不等式,為我們提供了多種巧妙放縮的途徑,我們可以根據證明的需要合理選取其中一個來達到不等式證明的目的. 原題的右邊需證明x1+x2 方法1 根據f(x1)=f(x2),即x1(1- lnx1)=x2(1-lnx2),且0 所以φ(t)在(1,+∞)上單調遞減,故t>1時,φ(t)=(t-1)ln(1+t)-tlnt<φ(1)=0,即得證x1+x2 點評上述兩種解答都充分體現了數學核心素養對解題的思路引領.兩種解法分別建立了對應的數學模型,通過逐步深入的邏輯推理和數據分析、數學運算簡化問題,最后使問題得以輕松解決.放縮法是證明不等式的常用方法,方法1利用不等式性質放縮,方法2利用對數切線不等式lnx≤x-1進行有目標的放縮,能達到事半功倍的效果.其中利用比(差)值代換是解決極值點偏移的另一種簡單快捷的方法,利用兩數之比(差)作為變量t,繼而將所求解問題轉化為關于t的函數問題求解,將雙變量問題轉化為單變量問題,從而實現消元的目的. 極值點偏移問題在全國高考中屬于高頻題型,此類問題由淺入深,對計算難度、思維深度的要求逐步提高,很好地體現了數學的科學性、應用性和創造性.解決這類問題,本質上就是將雙變量問題轉化為單變量問題,建立相應的數學模型,通過逐步深入的邏輯推理和數據分析、數學運算簡化問題,最后使問題得以輕松解決.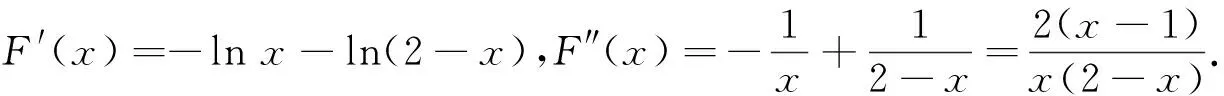
3.2 利用對數平均不等式
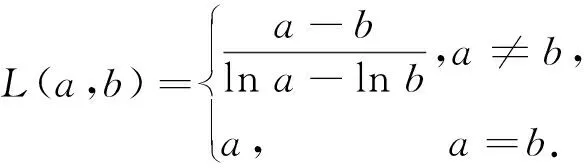
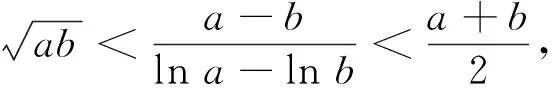
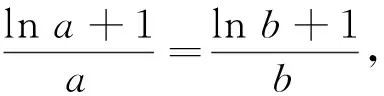
3.3 消元構造一元函數