一道課本習題的溯源、破解與思考
張志剛 (山東省寧陽縣復圣中學 271400)
徐章韜教授提出,理想的課堂是“學術”“技術”“藝術”三“術”交織的課堂.作為教師,其修為要能“上通數學、下達課堂”,能做“頂天立地”之事.然三“術”的發展具有序列性,先要解決一些“技術”問題,首先表現在教師能深刻研讀教材,能看到教材背后的“微言要義”.課程教材承載的是傳統成熟內容,是數學工作者集體智慧的結晶,不僅具備完整的學科知識體系,同時也是教師實施教學和學生學習的重要材料,而作為教材重要組成部分的習題理應置于顯著的位置上.眾多高考試題和競賽試題都是從課本例題或習題出發,經過改編、綜合、拓展、嫁接而來,具體表現為:課本例題、習題數據的變更,課本例題、習題條件的拓展,課本例題、習題背景的變換,課本例題、習題的應用等[1].對典型習題的深度挖掘有利于我們發現問題的內涵和本質,“揭秘”題目背后的故事與歷史淵源,概括歸納深藏其中的思維主線,以此為中心推而廣之,可以收到以一敵百的良好成效.事實上,“小題深挖”“一題多法”“一題多變”“多題一法”充分體現了教學的簡約性功能,能在盡可能短的時間內傳播盡可能多的數學思想,對題海戰術也是一種“反制”,歷來都是我國習題課教學的寶貴經驗,在繼承與發展的道路上,我們應使其煥發新的生機.下面舉例說明.
1 題目再現
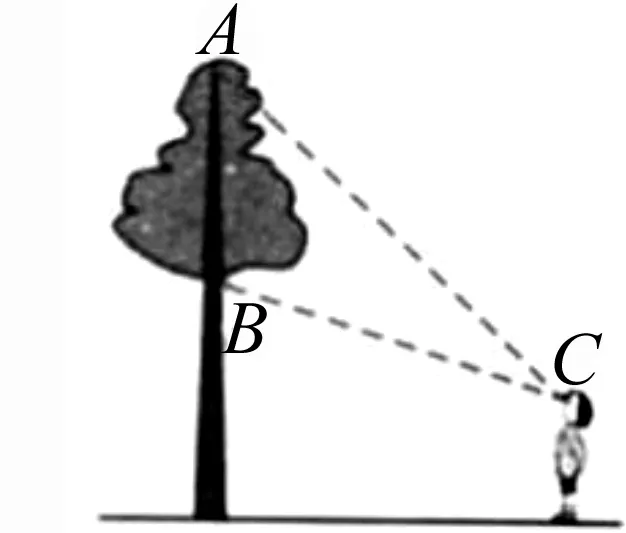
圖1
普通高中課程標準試驗教科書必修《數學5》(人教版2007年1月第3版,A版)第101頁習題3.4B組第2題:如圖1,樹頂A離地面am,樹上另一點B離地面bm,在離地面cm的C處看此樹,離此樹多遠時視角最大?
2 問題剖析
2.1 問題探源
本題源于歷史上經典的米勒問題.1471年,德國數學家、天文學家米勒(Johannes Miller)向諾德爾(Christian Roder)教授提出了一個有趣的問題:在地球表面的什么部位,一根垂直的懸桿呈現最長(即可視角最大)?上述最大視角問題因是米勒首先提出的,故被稱為“米勒問題”.米勒問題廣泛存在于各種實際問題中,例如探求欣賞一幅畫的最佳角度、足球比賽最佳射門點等.
2.2 數學模型
歷史上的米勒問題涉及的范圍是三維空間.作為實際問題,我們首先要做的是根據實物背景抽象出簡化的數學模型.相對于懸桿而言,地球的體積是相當大的,我們可視地球表面為平面,為了簡化模型,同時忽略觀察者身高對答案的影響,可以設觀察者的身高為0,且懸桿在地面上的投影也為0,因為懸桿垂直于地面,所以距點O相同距離的點所得可視角是相同的(圖2).
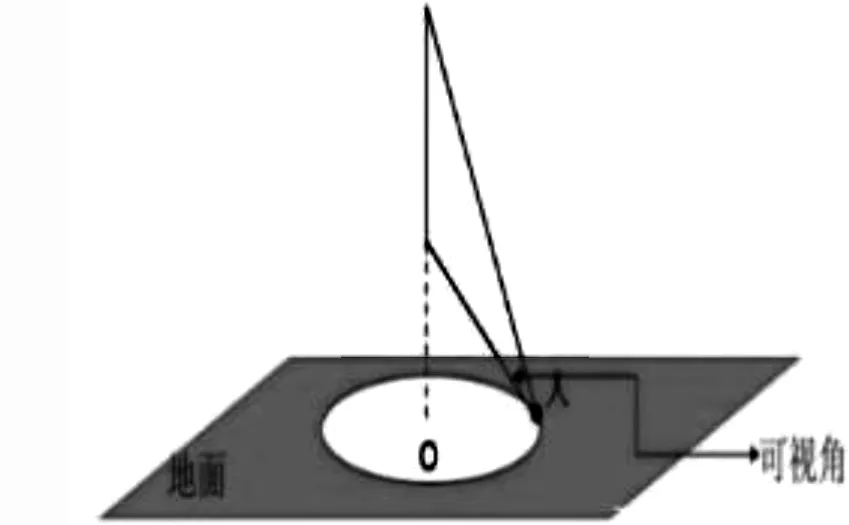
圖2
2.3 問題轉化
將上述模型一般化,可得到如下數學問題:如圖3,設M,N是銳角∠AOB的一邊OA上的兩點,試在邊OB上找一點P,使∠MPN最大.
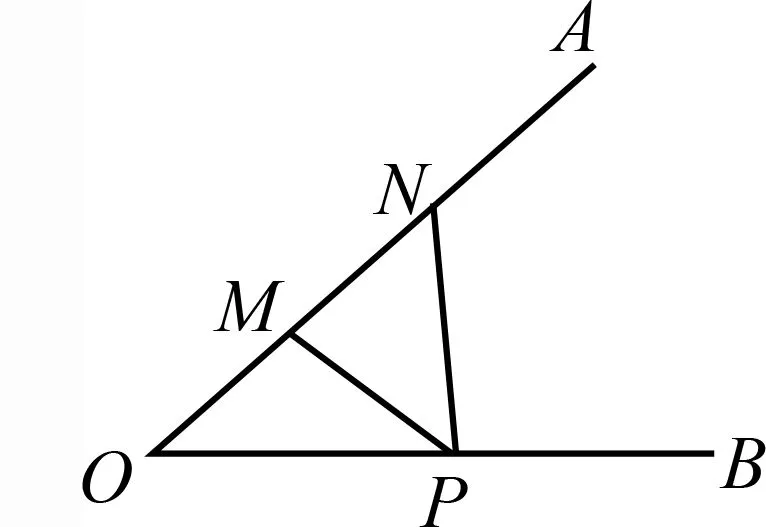
圖3
對上述米勒問題,我們有如下重要結論,不妨稱之為米勒定理:
米勒定理 設M,N是銳角∠AOB的一邊OA上的兩點,點P是射線OB上異于點O的一個動點,則當且僅當△MNP的外接圓與射線OB相切于點P時,∠MPN最大.
證明如圖4,在射線OB上任取異于P的一點P′,連結MP′,NP′,NP′與圓相交于點C,易知∠MCN>∠NP′M.又因為∠MCN=∠MPN,所以∠MPN>∠MP′N.得證.
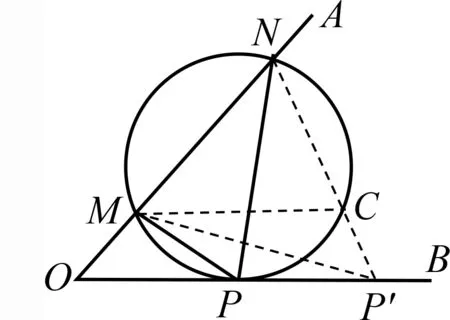
圖4
3 問題解答
3.1 幾何視角
解法1由圓的幾何性質探求張角最大值.
如圖5,DE是過點C且垂直于AB的直線,D為垂足.當DE與過點A,B的圓相切時,切點記為C,此時∠ACB=α最大.
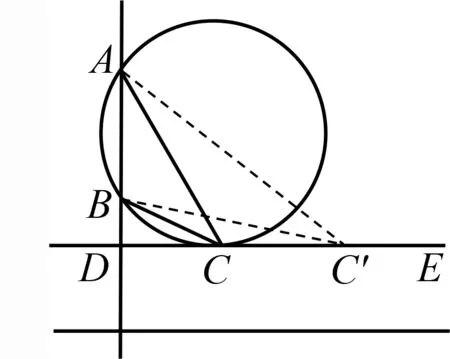
圖5

3.2 代數視角

解法2探索銳角∠ACB正切的最大值.

圖6

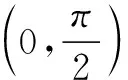
4 定理應用
以米勒問題為背景的最大張角問題在歷年高考試題中屢見不鮮而又經久不衰,如1986年高考全國卷理科第5題、2005年高考浙江卷理科第17題、2010年高考江蘇卷第17題等,若能從題設中挖掘、識別出隱含的米勒問題模型,將有效地突破思維瓶頸,大幅減少運算量,降低思維難度,從而使問題順利獲解.倘若無法及時提取該模型,很容易成為考生難以逾越的一道鴻溝.值得關注的是,米勒問題在競賽數學中也頻頻亮相,需要引起足夠的重視.下面列舉幾例.
題1(2004年全國高中數學聯賽第12題)在平面直角坐標系xOy中,給定點M(-1,2),N(1,4),點P在x軸上移動,當∠MPN取最大值時,點P的橫坐標為.(參考答案:1)
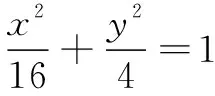

5 核心素養價值思考
從以上分析可以看出,米勒問題內蘊豐富,其解決過程需要直觀想象、數學建模、數學運算、邏輯推理等核心素養,具有較高的挖掘價值.而直觀想象素養是借助幾何直觀和空間想象感知事物的形態與變化,利用空間形式特別是圖形來理解和解決數學問題的素養.主要包括:借助空間形式認識事物的位置關系、形態與運動規律;利用圖形描述、分析問題;建立數與形的聯系,構建數學問題的直觀模型,探索解決問題的思路.[2]直觀想象是發現和提出問題、分析和解決問題的重要手段.在數學研究的探索中,通過運用直觀手段以及借助直觀展開想象從而發現結論、作出猜想的例子比比皆是.直觀想象在數學活動中是探索和形成論證思路、進行數學推理、構建抽象結構的思維基礎.史寧中教授在《普通高中數學課程標準(2017年版2020年修訂)解讀》中提出的案例5-9本質上也是典型的米勒問題,他還以此為例說明了直觀想象素養的三個水平.
案例5-9足球場上豎立一個電影屏幕,屏幕高為L,底部距離地面為H.設一人站在足球場上,眼睛距離地面高度為h,r=H-h>0.問:此人應該站在足球場上何處觀看電影,眼睛觀察屏幕上下沿形成的視角最大?

圖7
用豎直的線段AB表示屏幕,用EF表示站立的人,E點為眼睛的位置,觀察屏幕的上、下沿,形成視角θ=∠AEB,畫出平面圖(圖7).學生能描述和表達數學問題:設AB=L,BD=H,CD=EF=h,求點F的位置,使得視角θ最大.如此,學生能夠建立事物的幾何圖形,體會圖形和數量的關系,即達到了水平一的標準.
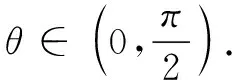
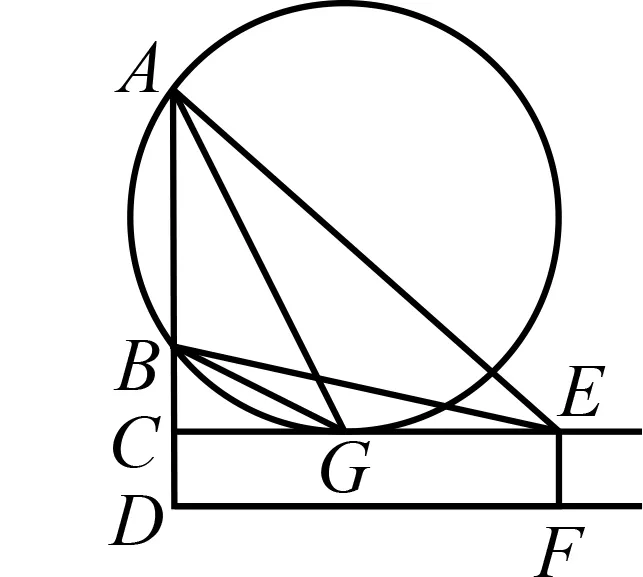
圖8
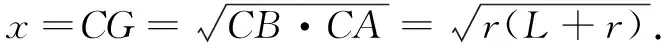
課程標準指出,直觀想象主要表現為以下四點:建立數與形的聯系,利用幾何圖形描述問題,借助幾何直觀理解問題,運用空間想象認識事物.米勒問題的解決過程是直觀想象素養的完美演繹,是數形結合、轉化與化歸、函數與方程等數學思想應用的集中體現,是不可多得的訓練素材和載體,極具教育價值.

