華南區域模式在湖南省的2 m溫度預報檢驗與訂正研究

陳 龍,陳靜靜,蘭明才,周長青,付 煒

(1.湖南省氣象臺，湖南 長沙 410118；2.氣象防災減災湖南省重點實驗室，湖南 長沙 410118；3.湖南省永州市氣象局，湖南 永州 425000)

0 引言

隨著社會經濟的快速發展，政府和公眾對氣象預報的關心程度日益增強，對氣象預報服務的精細化、精準化程度要求不斷提高。溫度作為氣象預報的基本要素，其精細化預報已成為天氣預報技術發展研究熱點。湖南地形呈向北開口的平原與三面環山的馬蹄狀特點，天氣系統影響復雜，精細化溫度預報成為湖南地區天氣預報的難點之一。

高分辨率數值預報模式的發展為精細化天氣預報提供了豐富的客觀產品，但由于大氣混沌效應、數值模式初始場誤差以及物理過程難以完美體現等問題，數值模式預報存在不可避免的系統性偏差。因此，發展合適的偏差訂正技術有助于提高溫度預報的精細化、精準化程度。為了減小模式誤差，一方面可以通過資料同化改善初始場或改進模式框架[1-6]等途徑，提高數值模式預報準確性；另一方面，可以利用客觀訂正技術[7-11]改進預報偏差，提升模式適用性。

預報檢驗是數值模式應用與訂正的基礎。我國學者陸續開展了全球數值模式和區域數值模式溫度預報的本地化檢驗評估工作，各模式呈現出季節、日變化、地域、復雜地形等系統性偏差。全球模式中，ECMWF、GRAPES_GFS和T639溫度預報均能較好地反映出溫度日變化特征，ECMWF整體表現較好，在中國區域整體預報偏低，整點溫度、高低溫預報存在明顯的季節和地域差異，東部預報效果優于西部，低溫預報效果明顯優于高溫預報[12-14]。近幾年，隨著預報業務對精細化程度要求的提高，國內自主研發的中尺度區域模式快速發展，由于模式框架、同化系統和空間分辨率等不盡相同，對溫度預報表現各異[15-19]。各區域模式也能較好地表現溫度日變化與季節特征，GRAPES_Meso低溫預報優于高溫預報，偏差表現呈東低西高[15]；針對短臨預報的GRAPES_RAFS溫度預報高原和復雜地形區域呈系統性偏低，華北、南疆地區預報偏高[16]；華中、華南區域模式溫度預報效果優于GRAPES，華中區域模式預報暖季優于冷季，華南區域模式則表現出高溫預報階段偏差明顯，夏季預報偏低，冬季偏高[17-20]。

發展模式預報客觀訂正技術是解決模式系統性偏差的有效途徑之一。現有研究多基于單模式或多模式，利用等權或非等權的誤差訂正方法改進溫度預報。一元線性回歸、多元線性回歸、消除偏差集合平均、MOS、卡爾曼濾波和超級集合預報等方法均能有效減小溫度多時效預報偏差[21-26]。

湖南現有溫度客觀預報僅基于溫度預報因子訂正，未考慮多因子對溫度的影響，因此，利用華南區域模式的更新快、精度高等特點，本文在華南區域模式2 m溫度預報偏差分析的基礎上，建立基于多因子影響的逐步回歸訂正模型，旨在提高2 m溫度預報準確性，為預報員提供更為精準的溫度預報參考依據。

1 資料與方法

1.1 資料說明

本文所用資料包括湖南97個國家站逐小時2 m溫度實況數據，華南區域模式(CMA-GD)各層預報產品和根據模式計算得到的溫度平流、渦度、散度預報產品，總計165個預報因子，空間分辨率3 km×3 km，反距離權重插值到湖南97個站點。模式預報與實況數據選取時段為2019年8月—2020年7月，模式起報時間為00、12時(世界時，下同)，預報時效為0～84 h，其中2、8月為檢驗數據集，訓練數據集根據訂正思路分別選取①全年、②冬半年(11月—次年4月)、③夏半年(5—10月)。根據業務實際需求，建模預報時間為起報時間往后的13～84 h預報(為方便對結果進行分析，下文以1～72 h代稱)。

1.2 逐步回歸法

綜合考慮多因子對2 m溫度的影響，通過對165個因子與實況2 m溫度的相關分析進行初篩，各站因子初篩標準為通過0.05顯著性水平檢驗，再選取與20%以上站點相關性均較好的25個因子作為變量引入逐步回歸方程，初選因子見表1。

表1 華南區域模式預報初選因子

逐站建立模型，引入多個變量構建回歸模型并進行檢驗，刪除不顯著變量，最終得到包含顯著變量的逐步回歸方程。逐步回歸方程如下：

(1)

式中，y1,y2,…,yn為2 m溫度因變量，β0,β1,…,βp為p+1個待估計系數，x11,x12,…,xnp是n次回歸引入的p個預報因子，設e1,e2,…,en是n個相互獨立的且遵從同一正態分布N(0,σ)的隨機變量。

1.3 檢驗方法

以平均誤差、平均絕對誤差、均方根誤差和預報準確率為指標，對比模式訂正預報、模式預報與實況結果，討論華南2 m溫度預報與訂正效果。

預報準確率即中國氣象局對各省市氣象部門的考核標準，反映預報相對于實況的預報效果，詳見公式(2)。

(2)

式中，N為預報個數，當預報與實況之差的絕對值≤2 ℃時，表示預報正確，NA為預報正確個數。當CR為1時，即準確率達到100%。

2 結果分析

2.1 2 m溫度預報檢驗

分析實況與華南區域模式2 m溫度預報，大部分站點的相關系數大于0.9，以龍山站為例(圖略)，每日00時起報的逐小時溫度預報與實況的相關系數達0.942，平均絕對誤差為2.153 ℃，均方根誤差為2.809 ℃，華南區域模式與實況變化趨勢基本一致，能較好地反映2 m溫度的日變化特征。

分析華南區域模式00、12時起報的1～72 h逐24 h 2 m溫度預報，97站的平均準確率分別為0.58、0.42，均方根誤差分別為2.84 ℃、4.1 ℃，00時起報的2 m溫度預報明顯優于12時起報的。00、12時起報的1～72 h預報中， 24 h預報準確率最高，分別為0.63、0.44，均方根誤差最小，為2.5 ℃、3.99 ℃，預報效果明顯優于48 h、72 h預報。

2.1.1 逐時預報檢驗 通過分析華南區域模式00時起報的1～72 h逐時2 m溫度預報，探討華南區域模式逐時2 m溫度預報偏差。從圖1a、b來看，準確率與均方根誤差均呈明顯日變化，白天12～21 h、36～45 h、60～69 h(即北京時的08—17時)時段，準確率明顯下降，均方根誤差明顯上升，正午時段預報準確率達到最低、均方根誤差達到最大；夜間，即每日09時—次日00時，準確率均在上升后維持在1 d中的最高水平，均方根誤差保持最小。從平均誤差與平均絕對誤差來看(圖1c、d)，華南區域模式白天時段誤差更大，以負偏差為主，夜間時段存在正偏差，在日出和日落時分，誤差達到最大。隨著預報時效的延長，模式預報呈準確率下降、誤差增大趨勢。

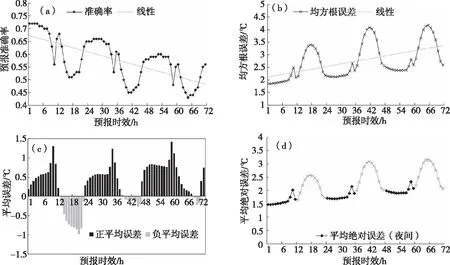
圖1 湖南地區00時起報1～72 h逐時2 m溫度預報準確率(a)、均方根誤差(b)、平均誤差(c)、平均絕對誤差(d)

2.1.2 1～24 h逐月檢驗 分析華南區域模式00、12時起報的1～24 h逐月2 m溫度預報(圖2)，探討華南區域模式2 m溫度預報月、季偏差。00時起報的2 m溫度預報中，8月平均準確率最低、均方根誤差最大，分別為0.5、2.76 ℃；1月準確率最高、均方根誤差最小，分別為0.71、2.14 ℃；夏半年(5—10月)整體準確率明顯低于冬半年(11月—次年4月)，均方根誤差也偏大。12時起報的2 m溫度預報在8月準確率最低、1月準確率最高，除1月外，冬半年均方根誤差較高。00時起報的2 m溫度預報效果明顯優于12時起報。

圖2 湖南地區00時、12時起報1～24 h 2 m溫度預報逐月均方根誤差(a)及準確率(b)

2.1.3 2 m溫度預報偏差的空間分布 通過分析華南區域模式00、12時起報的1～72 h 2 m溫度預報平均準確率、均方根誤差的空間分布，探討華南區域模式在湖南不同地區的預報效果。從均方根誤差來看(圖3a、b)，00時起報的2 m溫度預報整體偏差較小，均方根誤差大部分站點在2～3 ℃，南岳站及個別海拔較高站點、湖區站點偏差偏大；12時起報的2 m溫度預報整體偏差較大，均方根誤差集中在4～5 ℃，湘東、湘西南部分站點在3～4 ℃。從準確率來看(圖3c、d)，00時起報的2 m溫度預報準確率大部站點在0.5以上，海拔稍高地區預報優于平原與谷地；12時起報的2 m溫度預報大部站點準確率在0.5以下，湘東北部分站點僅有0.3～0.4。受地形與模式系統性偏差影響，華南區域模式對湖南不同區域2 m溫度預報效果不同，湘西整體優于湘東。對大部分站點，00時起報的2 m溫度預報效果明顯優于12時起報。

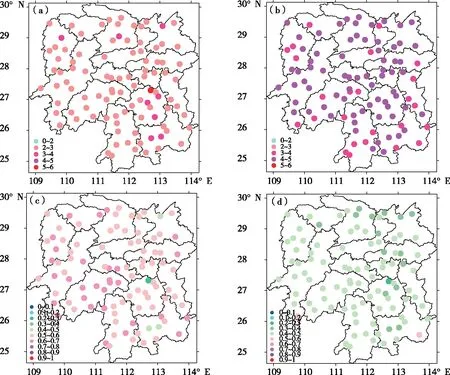
圖3 湖南地區00、12時起報1～72 h 2 m溫度預報平均均方根誤差(a、b，單位：℃)及準確率(c、d)空間分布

2.2 逐步回歸訂正檢驗

2.2.1 不同起報時次的溫度訂正 分別對1～72 h逐時包含00、12時起報的模式預報數據集與00時、12時起報的模式預報數據建立逐步回歸模型，結果顯示(圖4)，分起報時次的訂正結果相較于不分起報時次建模的訂正結果平均絕對誤差、均方根誤差更小，準確率也略優，兩者較直接模式預報而言，均有正技巧。分與不分起報時次建模訂正的2 m溫度，00時起報的訂正結果均優于12時起報，兩者均優于模式預報。

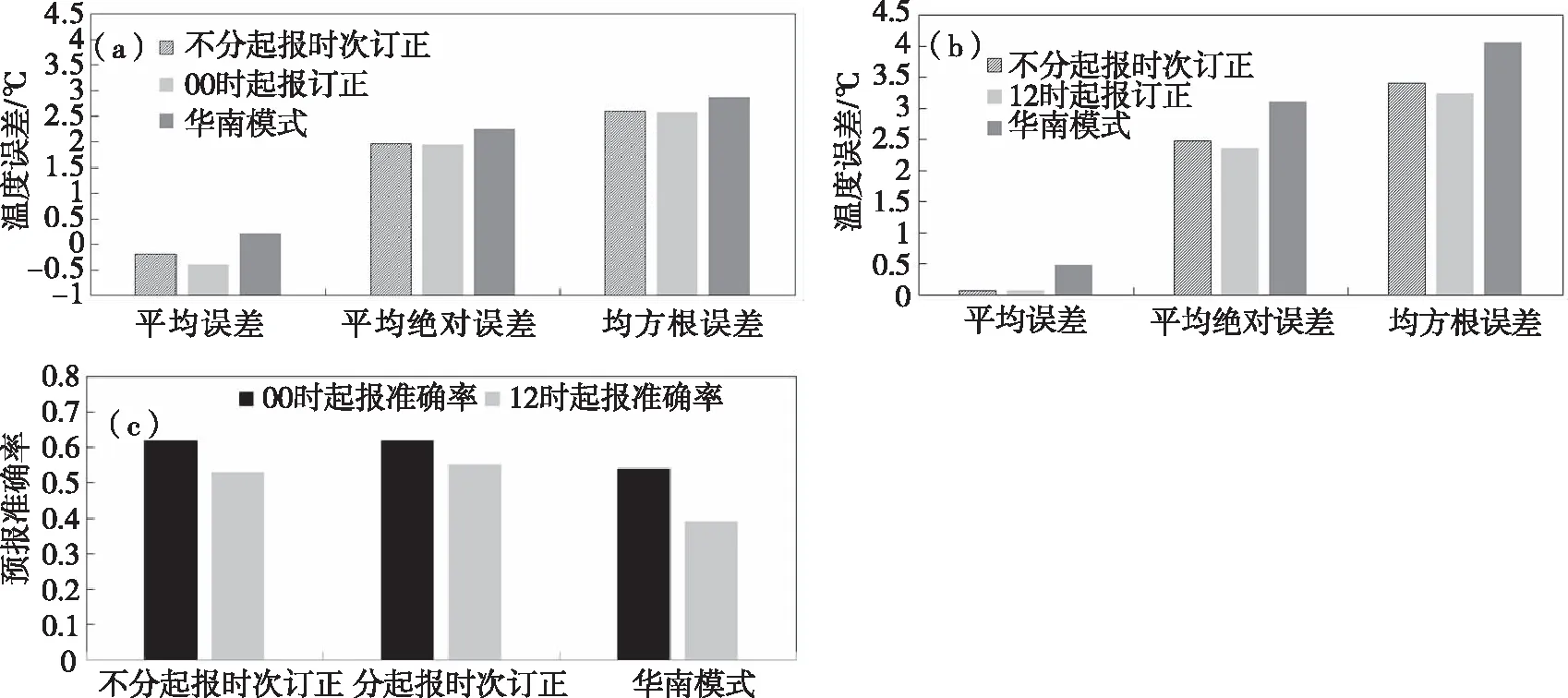
圖4 湖南地區分與不分起報時次2 m溫度訂正預報平均誤差、平均絕對誤差、均方根誤差(a)(b) (單位：℃)及準確率(c)

2.2.2 不同時段的溫度訂正 以不同起報時次建模為基礎，將1～72 h作為整體數據集與分別包含1～24 h、25～48 h與49～72 h的數據集建立逐步回歸模型。結果顯示(表2、圖5)，以1～72 h為整體的建模訂正結果，1～24 h的訂正準確率優于25～48 h、49～72 h，隨著預報時效延長，訂正效果下降，各時段00時起報訂正結果準確率均優于12時起報，基于逐步回歸的訂正產品優于模式預報。00、12時起報的分時段建模訂正結果準確率相對于不分時段的訂正結果無明顯變化，誤差略有增加。

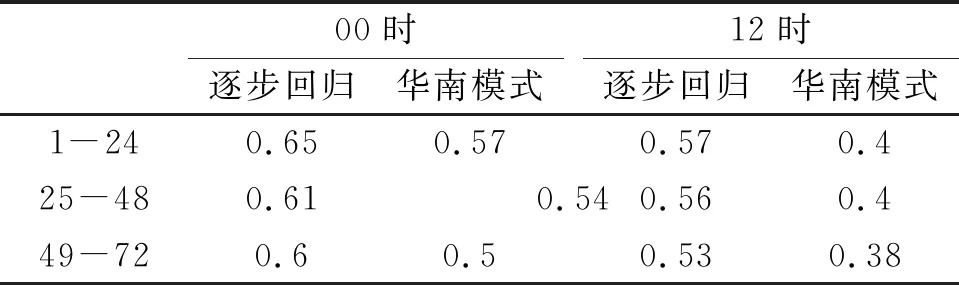
表2 00時、12時分起報時次不分時段的2 m溫度訂正預報準確率

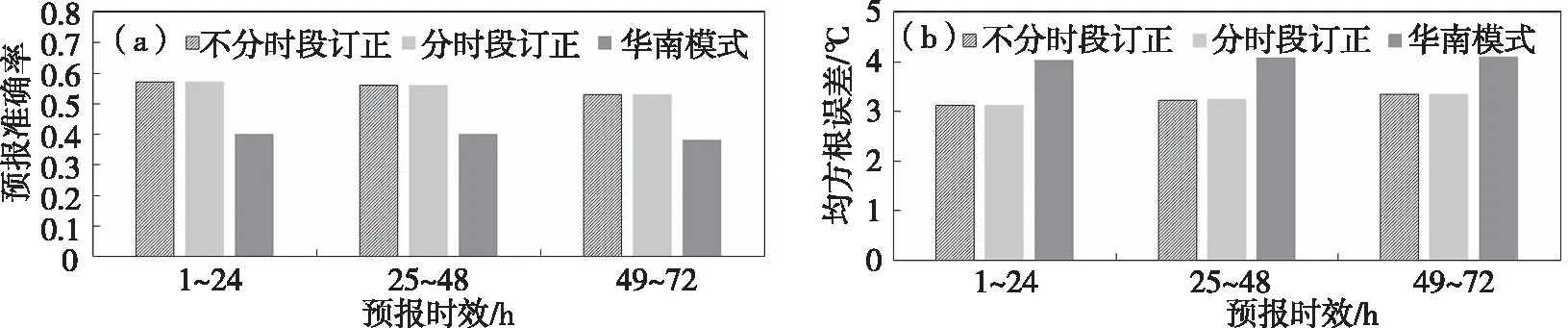
圖5 12時起報分時段的2 m溫度訂正預報準確率(a)與均方根誤差(b)

2.2.3 不同季節的溫度訂正 以分起報時次、1～72 h作為整體建模為基礎，將1—11月作為整體數據集與分別以冬半年11月—次年4月、夏半年5—10月的數據集建立逐步回歸模型。結果顯示(表3)，分季節的5—10月建模、11月—次年4月建模的訂正結果準確率均高于不分季節建模的訂正結果，均方根誤差也有明顯下降，8月訂正效果更為明顯。基于逐步回歸的訂正產品相對于模式預報均呈正技巧。

表3 分與不分季節的2 m溫度訂正預報準確率與均方根誤差(單位：℃)

2.2.4 分起報時次和季節訂正結果的空間分布 根據前文分類建模結果分析，以分起報時次、不分時段、分季節建立數據集，對湖南97個國家站分別建立逐步回歸模型，以2、8月作為檢驗時段，通過分析訂正結果對模式的準確率差值(技巧)，探討基于逐步回歸的華南區域模式2 m溫度訂正產品的空間訂正效果。結果顯示(圖6)，00時， 2月，山區有明顯的正技巧，平原地區大部站點訂正效果略差； 8月，平原與山區具有正技巧，平原地區訂正效果更明顯。12時，2、8月均有正技巧，8月訂正效果顯著，平原訂正效果優于山區。

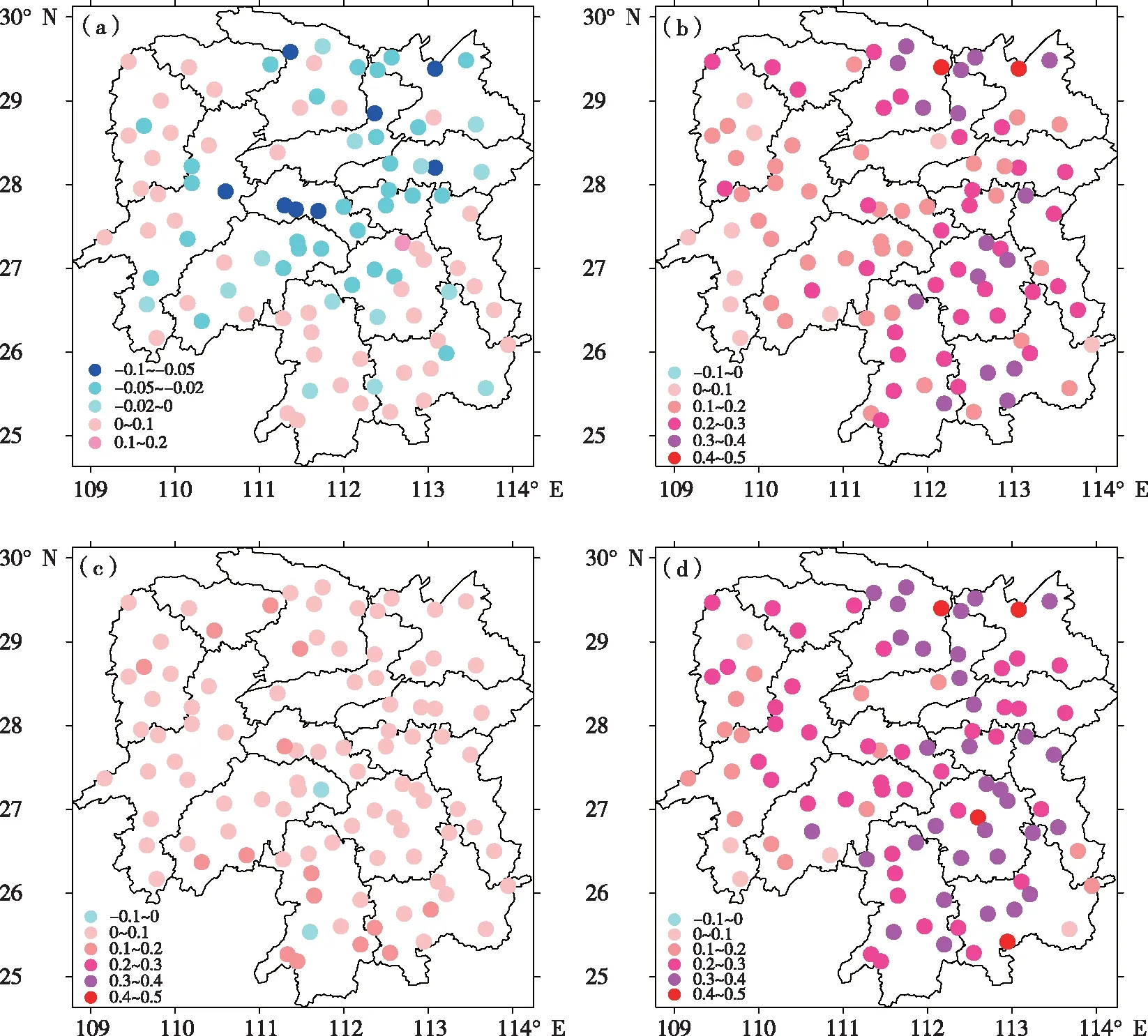
圖6 分季節2 m溫度訂正預報與模式預報準確率差值空間分布(00時起報2月(a)、8月(b)，12時起報2月(c)、8月(d))

3 結論

①華南區域模式與實況變化趨勢基本一致，能較好地反映2 m溫度的日變化特征。逐時2 m溫度預報誤差呈明顯日變化，白天誤差增大、準確率下降，夜間預報效果相對較好；溫度預報在日出和日落時段負偏差最大；模式預報夏半年準確率明顯低于冬半年；隨著預報時效的延長，模式對2 m溫度預報能力下降。受模式系統性偏差影響，華南區域模式對湖南不同區域2 m溫度預報效果不同，湘西整體優于湘東，海拔稍高地區預報優于平原與谷地。00時起報的2 m溫度預報效果優于12時起報的。

②基于逐步回歸對華南區域模式2 m溫度預報在不同起報時次、不同時段、不同季節建立的模型，其結果相對于直接模式預報均有正技巧，其中，分起報時次訂正結果更優；分時段訂正結果無明顯優勢；分季節訂正結果明顯好于全年訂正結果。分起報時次、不分時段、分季節建立的逐步回歸訂正模型相對模式預報有較大的提升，不同季節訂正效果不同。

③采用逐步回歸模型訂正的2 m溫度客觀預報在空間上技巧表現存在差異。00時，2月山區有明顯的正技巧，平原地區訂正效果略差；12時，2、8月均有正技巧，平原訂正效果優于山區。