曲線矮塔斜拉橋在不同曲率半徑下力學性能分析

高碧波 黃 昊

(1.中國鐵路設計集團有限公司，天津 300308；2.沈陽建筑大學交通工程學院，沈陽 110168)

隨著橋梁建設事業的發展，為了滿足交通路線設計的需求，曲線矮塔斜拉橋作為一種新型的橋梁結構在鐵路交通領域越來越被廣泛應用[1]。

矮塔斜拉橋是連續梁橋和斜拉橋之間的一種過渡橋型[2]，適合鐵路橋梁較大的剛度設計需要，同時具有梁高較小、后期徐變變形小、造型美觀、經濟指標好等優點[3]。曲線矮塔斜拉橋存在較大的彎扭耦合效應，受力復雜，提高了橋梁設計難度，亟需開展曲線矮塔斜拉橋受力性能的影響研究[4]。國內眾多學者對該類橋型的結構體系和相關參數進行研究[5]。張欣欣結合池黃高鐵大跨度三塔矮塔斜拉橋設計，對結構體系、合理結構參數等關鍵技術進行了分析[6]；朱佩章等以某大跨度曲線矮塔斜拉橋為研究對象，研究分析了剪力滯、箱梁畸變、扭轉等空間效應對梁體應力的影響[7-8]；馬力雄結合某曲線矮塔斜拉橋的設計，研究分析該類橋型的彎扭耦合受力特點，并通過有限元計算進行了驗證[9]；劉康結合某曲線斜拉橋的設計，研究分析了曲率半徑和塔高對斜拉橋靜力特性的影響[10]。

綜上所述，曲線矮塔斜拉橋的空間特性和受力狀態復雜，曲率半徑越小，橋梁設計難度越大，且工程造價提高。曲率半徑是影響曲線矮塔斜拉橋受力的主要參數。結合邯濟膠濟聯絡線跨膠濟高鐵特大橋主橋(120+120)m矮塔斜拉橋的設計，建立不同曲率半徑的有限元模型，對相關參數進行了研究和分析[11]，為曲線獨塔矮塔斜拉橋的設計提供參考。

1 工程概況

為了增大鐵路橋下凈空，減少對既有鐵路線的干擾，邯濟膠濟聯絡線跨膠濟高鐵特大橋主橋選用了曲線矮塔轉體斜拉橋的結構形式，該橋于2016年7月動工建設，已于2019年5月建成通車。主橋全長240 m，橋跨布置為(120+120)m。主橋位于圓曲線上，曲率半徑為800 m。主梁采用單箱雙室、變高度、變截面直腹板形式。中支點截面位置梁高7.0 m，跨中及邊跨等高段梁處截面高4.5 m，梁底下緣曲線按二次拋物線變化。一般箱梁節段頂寬16.1 m，底寬13.6 m，中支點處箱梁頂寬局部加寬至16.5 m。斜拉索橫向為雙索面，立面為半扇形布置。索塔高29.7 m，采用實心截面，每個索塔設10對斜拉索，橋塔豎向索距為1.1 m，梁部索距為8.0 m。該橋采用平面轉體施工法跨越既有膠濟高鐵，轉體角度43.5°，采用以球鉸中心支撐為主、環道支撐為輔的轉動體系，轉體噸位250 000 kN，屬轉體質量較大、長度較長的現澆轉體曲線獨塔矮塔斜拉橋。

以邯濟膠濟聯絡線跨膠濟高鐵特大橋主橋為研究對象，采用Midas Civil建立有限元模型。橋梁結構離散成210個節點，176個單元。同時建立中心線曲率半徑分別為400，600，800，1 000，2 000 m的曲線矮塔斜拉橋模型。各模型采用120 m+120 m相同的跨徑布置。其中，主梁截面采用梁單元模擬；橋塔和橋墩采用梁單元模擬；支座采用剛性連接模擬；斜拉索采用桁架單元模擬。圖1為曲率半徑800 m矮塔斜拉橋的有限元模型。

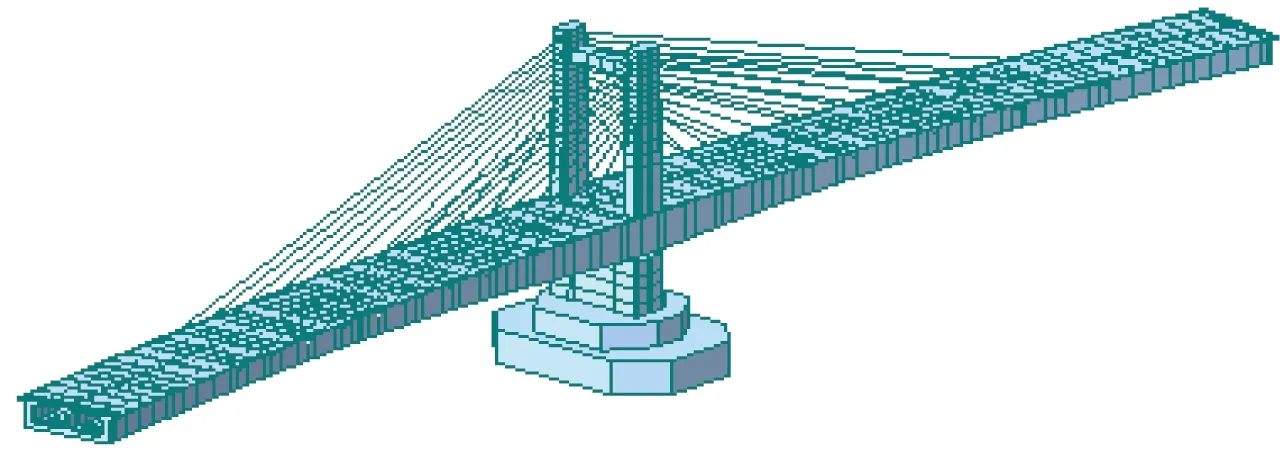
圖1 曲率半徑800 m的矮塔斜拉橋有限元模型

2 計算結果和分析

2.1 主梁內力與變形結果分析

圖2～圖4分別給出了不同曲率半徑下的曲線獨塔矮塔斜拉橋在初始成橋狀態下主梁扭矩、剪力和彎矩的最值的變化曲線。

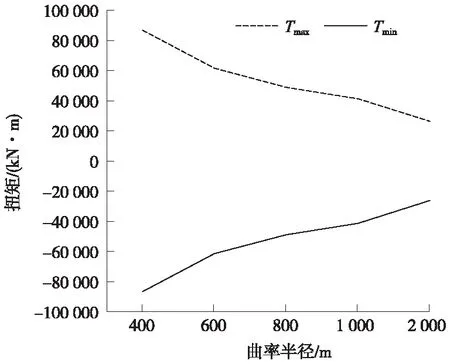
圖2 不同曲率半徑下主梁扭矩

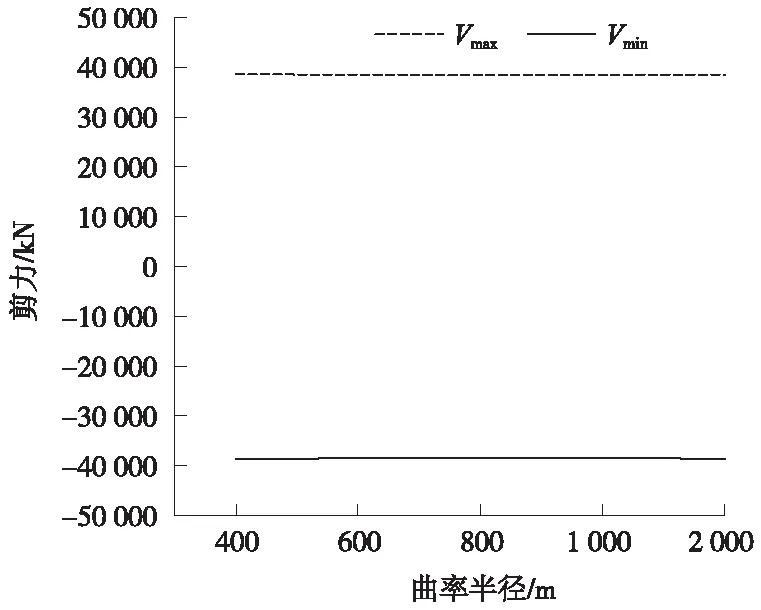
圖3 不同曲率半徑下主梁剪力

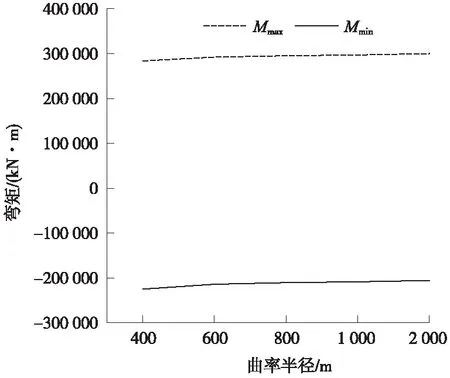
圖4 不同曲率半徑下主梁彎矩

由圖2可以看出，主梁扭矩隨著曲率半徑的減小而增大，曲率半徑越小，扭矩的增大也越明顯。當曲率半徑由2 000 m變為400 m時，扭矩增加值為60 443.4 kN·m，增大69.7%；由圖3、圖4可知，曲率半徑的變化，對主梁彎矩和剪力的影響均不大，變化趨勢接近一條直線。曲率半徑減小時，最大彎矩值略有減小，當曲率半徑由2 000 m變為400 m時，主梁彎矩減小幅度為5.4%，影響較小；最大剪力值改變很小，剪力最大值增大約0.25%，可以忽略。

曲率半徑越小，主梁扭矩越大，曲率半徑減小引起的扭矩增大應引起足夠重視[12]。主梁曲率半徑改變對彎矩和剪力影響不大，曲率半徑較大時，可按照展開的直線橋進行主梁預應力布置和配束檢算，可滿足主梁受力要求。

曲線矮塔斜拉橋經過10年收縮徐變，主梁墩塔梁固結處和邊跨端部處扭矩會發生變化。圖5和圖6分析了成橋10年后和初始成橋狀態，在不同曲率半徑條件下，主梁墩塔梁固結處和邊跨端部處扭矩的變化情況。

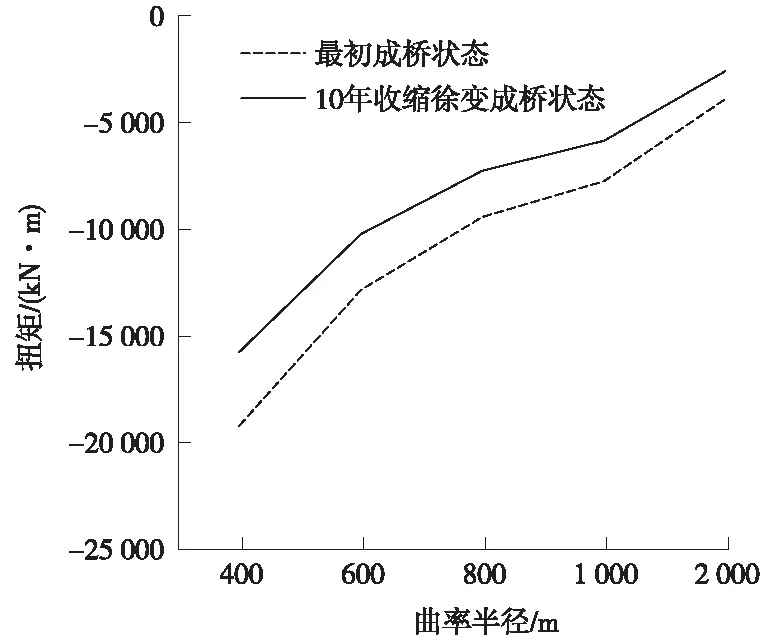
圖6 邊跨端部處扭矩變化

從圖5、圖6可以看出，相比初始成橋狀態，經過10年收縮徐變，不同曲率半徑下的橋梁，主梁扭矩均有不同程度的降低，收縮徐變使得主梁扭矩絕對值降低，降低幅度與曲率半徑無關，均是36%左右，對主梁受力有利。觀察主梁兩端扭矩值可以觀察到相同的規律。

圖7給出了初始成橋狀態下，曲線獨塔矮塔斜拉橋的主梁豎向撓度隨不同曲率半徑的變化曲線。

圖7 不同曲率半徑下主梁豎向位移

從圖7可以看出，主梁最大位移發生在最大懸臂端附近。隨著曲率半徑的減小，主梁豎向位移呈增加的趨勢，表明曲率半徑越小，主梁彎扭耦合效應越大，主梁變形就越大[13]。圖8給出了主梁跨中截面在最初成橋狀態與成橋10年下，豎向撓度隨不同曲率半徑的變化曲線。不同曲率半徑下，10年收縮徐變成橋狀態相比最初成橋狀態，跨中豎向撓度均有所減小，對受力有利。

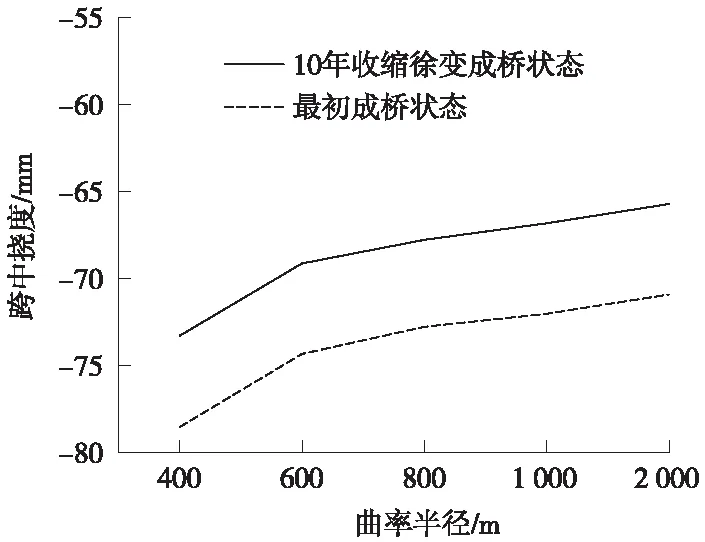
圖8 不同曲率半徑下主梁跨中撓度

2.2 主塔內力與變形結果分析

選取本橋曲線內側索塔進行分析，對最大懸臂狀態和最終成橋狀態的塔頂位移進行對比說明。塔頂橫向位移在兩個施工階段下隨曲率半徑變化見圖9。

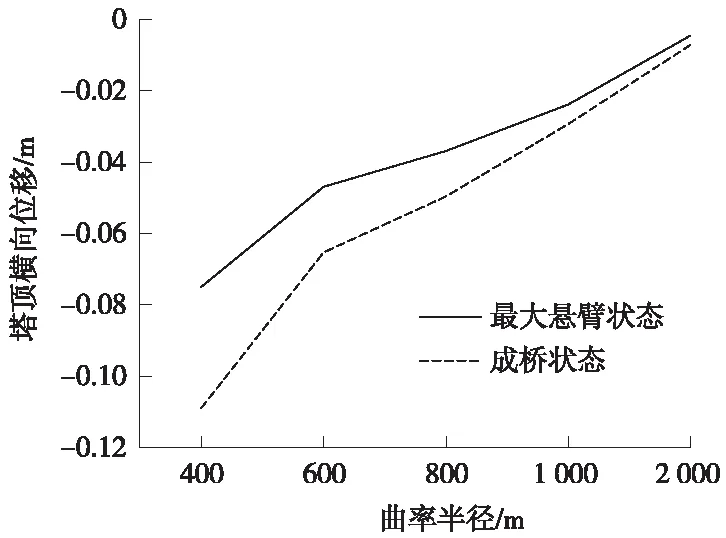
圖9 不同階段塔頂橫向位移隨曲率半徑變化

從圖9可以看出，無論是成橋狀態還是最大懸臂狀態，隨著曲率半徑減小，塔頂橫橋向位移增大。原因是因為曲率半徑越小，斜拉索橫橋向分力越大，橋塔變形加大。且成橋狀態相比最大懸臂狀態，橋塔橫橋向位移增大幅度較大。說明隨著施工階段的發展塔頂橫向位移有不斷增大的趨勢。

圖10給出了橋塔橫橋向彎矩隨著曲率半徑的變化情況。由圖10可知，隨著曲率半徑的減小，橋塔橫向彎矩有不斷增加的趨勢，橋塔受力越來越不利。這說明隨著曲率半徑減小，曲線獨塔矮塔斜拉橋產生的彎扭耦合作用越大，從主梁傳遞到橋塔上的荷載也越大，所以橋塔產生的橫向彎矩也相應增大。曲率半徑較小時，橋塔受力應引起足夠的重視，橫向彎矩較大時，可以通過配置普通鋼筋或者在橋塔內布置預應力鋼束來抵消橫橋向彎矩。觀察10年收縮徐變以及最初成橋狀態下橋塔受力差異，可以看出收縮徐變對橋塔受力影響不大。

圖10 橋塔橫向彎矩隨曲率半徑變化

2.3 索力結果分析

圖11給出了斜拉索索力值隨曲率半徑的變化曲線，其中曲線內側斜拉索編號為C1到C10，曲線外側斜拉索編號為C1′到C10′。圖12給出了最初成橋狀態下C5斜拉索索力值隨曲率半徑的變化情況。圖13給出了不同階段下索力變化情況。

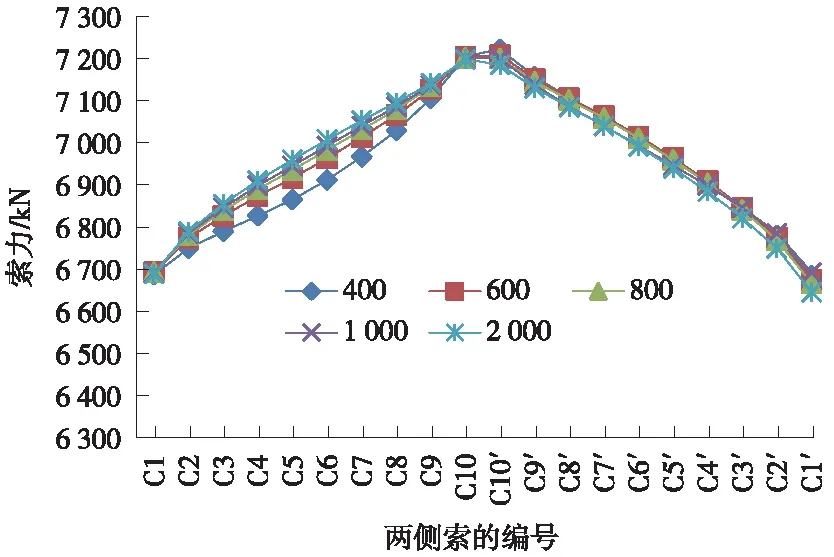
圖11 兩側斜拉索索力值

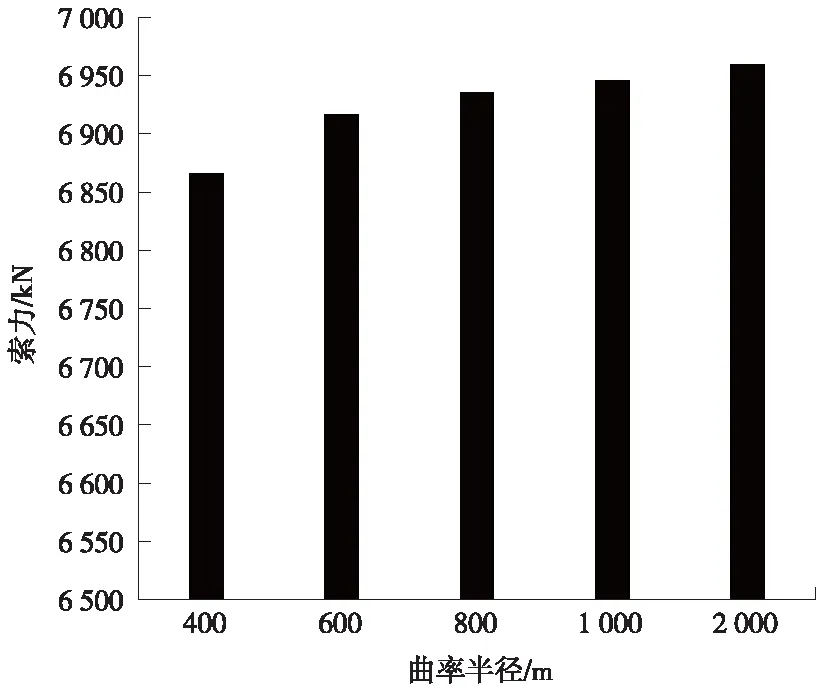
圖12 最初成橋狀態下斜拉索C5索力隨曲率半徑變化

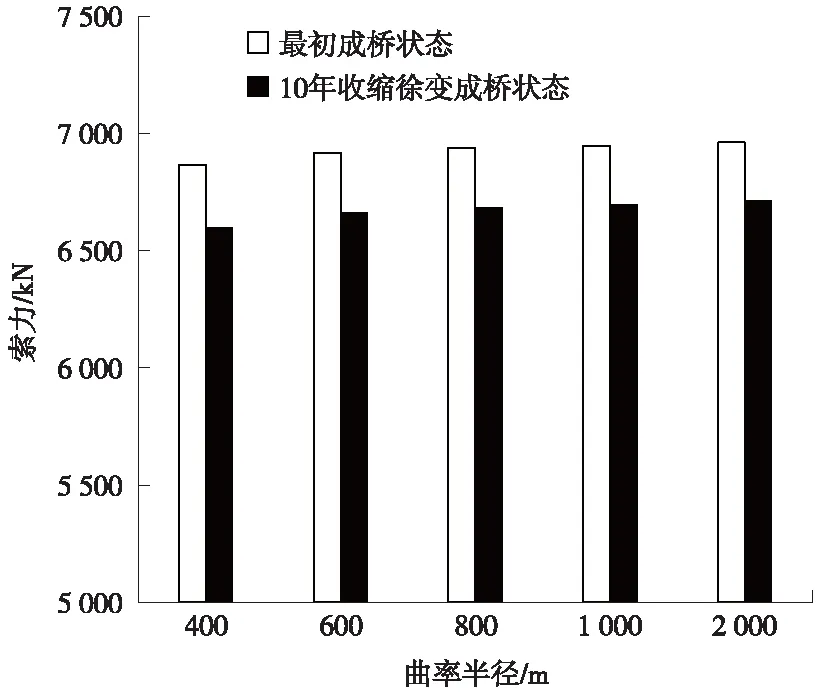
圖13 斜拉索C5在不同階段下索力變化

由圖11可知，隨著曲率半徑的變化，斜拉索索力值變化很小。因此，曲率半徑對斜拉索的索力值影響有限。選取C5斜拉索進行分析，由圖12可知，在最初成橋狀態下隨著曲率半徑的減小，斜拉索的索力值也呈減小的趨勢，但是索力減小幅度不大。并且隨著曲率半徑的減小，索力減小幅度增大。圖13給出了最初成橋狀態和10年收縮徐變狀態下的C5斜拉索索力值對比，可以發現在不同曲率半徑下，10年收縮徐變狀態下的索力均比最初成橋狀態的索力要小。

2.4 支座反力結果分析

在“主力+附加力”工況下，曲線獨塔矮塔斜拉橋在不同曲率半徑下內外側支座反力的變化規律見圖14、圖15。不同階段下支座P3的支座反力變化情況見圖16。

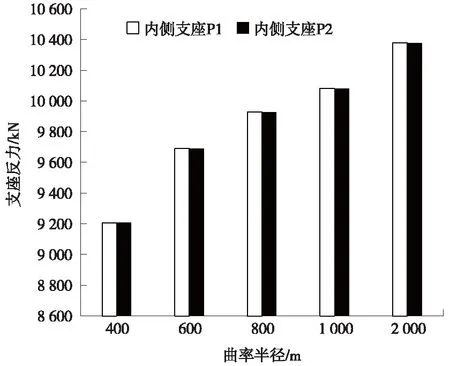
圖14 矮塔斜拉橋曲線內側支座反力對比

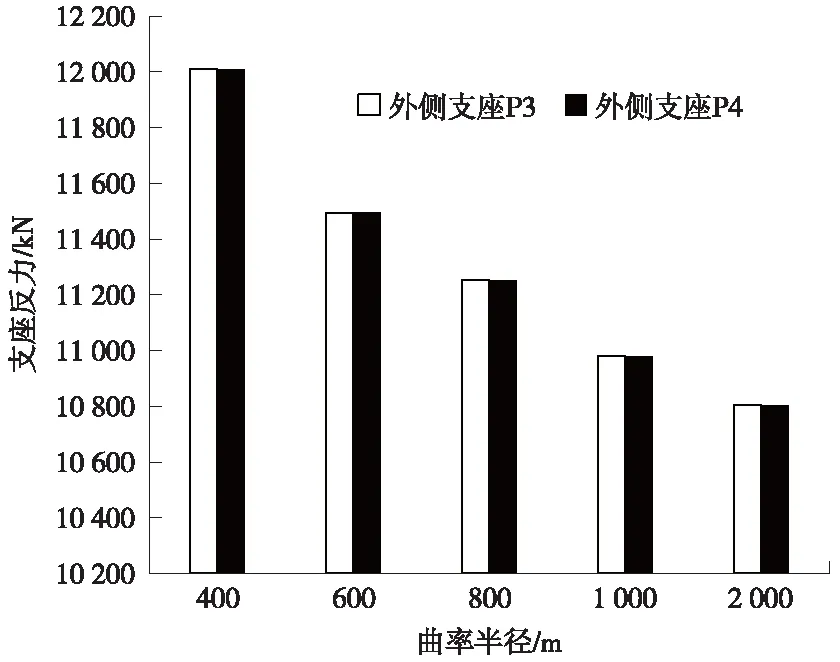
圖15 矮塔斜拉橋曲線外側支座反力對比

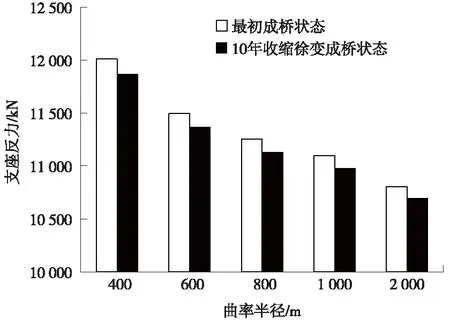
圖16 支座P3在不同狀態下的支座反力變化

由圖14和圖15可知，內側兩個支座P1和P2的支座反力大小幾乎相等，同樣的外側兩個支座P3和P4的支座反力大小也相等。從圖14可知，隨著曲率半徑的減小，內側支座的支座反力呈減少的趨勢。而從圖15可知，隨曲率半徑的減小，外側的支座反力呈不斷增大的趨勢。當曲率半徑從2 000 m減小到400 m時，內側支座反力從10 376.96 kN減小到9 204.64 kN，而外側支座反力從10 803.75 kN增加到12 009.32 kN。當曲率半徑為2 000 m時，內外側支座反力接近[14]。曲率半徑越小，主梁彎扭耦合作用越明顯，內外兩側的支座反力差距越來越大。曲率半徑較小時，對于曲線矮塔斜拉橋支座噸位的選擇應考慮內外側支座噸位的差別[14]。

從圖16可以看出，無論是初始成橋狀態，還是經過10年收縮徐變，隨著曲率半徑的減小，支座P3的支座反力增大。同一曲率半徑條件下，最初成橋狀態下的支座反力比10年收縮徐變成橋狀態下的大，這說明經過10年收縮徐變會導致支座反力減小[15]。

3 結論

依托邯濟膠濟聯絡線跨膠濟高鐵特大橋主橋主跨(120+120)m曲線矮塔斜拉橋，開展曲率半徑對獨塔矮塔斜拉橋受力及變形性能的影響規律研究，包括對主梁和主塔受力及變形，斜拉索索力以及支座反力等設計參數的影響規律，得出以下結論。

(1)獨塔矮塔斜拉橋曲率半徑越小，主梁受到彎扭耦合作用越大，主梁扭矩、橋塔橫向彎矩、塔頂橫向位移越大。主梁曲率半徑越小，主梁內外側邊支座受力差值越大，其中外側支座受力加大，內側支座受力減小。曲率半徑對斜拉索索力影響有限。曲線矮塔斜拉橋設計時，應注意主梁抗扭檢算，橋塔橫橋向受力的檢算以及支座選型時考慮曲率造成的內外側支座支反力的不同。

(2)曲線矮塔斜拉橋考慮10年收縮徐變時，主梁扭矩值及跨中豎向撓度相應減小，橋塔橫向彎矩和橫向位置值同樣相應減小，同時對斜拉索索力和支座反力影響相對較小。收縮和徐變改善了主梁和橋塔的內力和變形。

(3)曲線獨塔矮塔斜拉橋曲率半徑增大時，主梁彎扭耦合作用影響越來越小。同時由于主梁采用箱型截面，抗扭能力較強，當曲率半徑較大時，可近似的把曲線獨塔矮塔斜拉橋展開，按直線矮塔斜拉橋進行主梁受力的檢算。

(4)邯濟膠濟聯絡線跨膠濟高鐵特大橋主橋，通過計算對比分析，采用R=800 m的曲率半徑，在充分考慮彎扭耦合作用和10年收縮徐變帶來的影響條件下，采用預設偏心、橋塔設置預應力筋以及增設閉合抗扭鋼筋等措施，合理考慮了曲率半徑的影響。目前該橋已竣工，施工和運營效果較好。