基于火藥燃燒模型的彈射器工作過程數值模擬

劉 群，蔡文健，楊 昭，周傳霞

(北京空間機電研究所，北京 100076)

0 引言

火藥燃燒產生的高溫燃氣是大多數火工裝置工作的能量源，因此火藥燃燒特性是決定火工裝置工作性能的關鍵因素[1]。然而，火工裝置作動是一個高速瞬態過程，很難通過試驗獲得火藥燃燒和機械部件相互作用甚至發生破壞的細節。因此，建立火藥燃燒模型有助于解釋試驗結果，并有助于產品的設計改進。數十年來，國內外學者對火藥燃燒模型及其結構的作用過程進行了大量研究。Ng[2]開發了最早火工裝置驅動模型，稱為MAVIS，其中燃燒過程引起的質量和能量釋放并沒有直接建模，而是使用經驗公式確定的狀態方程來描述驅動活塞運動的壓力。Emery等[3]和Jones等[4]采用相同的方法對電爆閥內活塞運動的過程進行了建模計算。此后，研究者開始考慮火工裝置內火藥燃燒反應過程。他們的模型考慮了火藥燃燒釋放到氣體和凝聚相產物的能量隨時間的變化過程，但是這些能量在容腔內都是均勻分布。該模型由一系列以時間為變量的常微分方程組成[5-12]。以上學者建立的模型均假設火藥燃燒反應速率比裝置工作時間小得多。Lee[12]的工作探索了密閉容器內非穩態氣體動力學對裝置工作過程的影響，結果表明，當裝置工作時間與燃燒波傳播時間接近時，能量空間均勻分布假設無效。然而，Lee的模型未考慮火藥燃燒釋放能量過程，僅是將高壓不連續性能量入口作為模擬燃燒的初始條件。因此，以往的模型在預測和分析火工裝置性能時，沒有同時考慮火藥燃燒的能量釋放過程和燃燒腔內的壓力梯度分布。本文借鑒炸藥反應的多項式模型，建立了單項式火藥燃燒模型，模型能夠定量描述火藥燃燒過程以及容腔內的壓力分布，采用該模型對彈射器工作過程進行了數值模擬計算，計算結果與試驗結果吻合性較好，表明該燃燒模型能夠較真實地描述火藥燃燒過程，可以將該模型用于指導火工裝置設計。

1 單項式火藥燃燒模型

火藥燃燒反應是以燃燒波形式傳播，經典的火藥燃燒過程如圖1所示。假設火藥從左端點火，則會產生一個平面燃燒波向右傳播，燃燒波逐漸傳入未燃燒火藥，同時燃燒產物留在燃燒波后面，在未燃燒火藥和燃燒產物之間有一個相對寬的燃燒反應區，火藥在反應區內發生氣化并且反應。

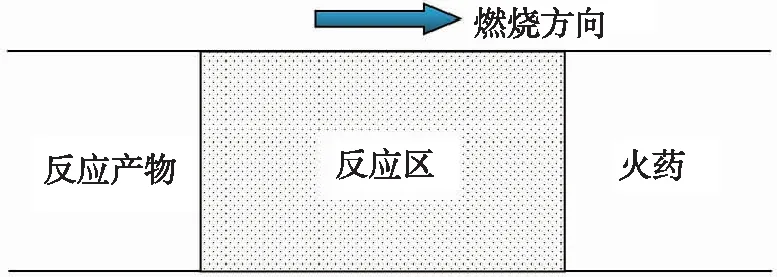
圖1 經典火藥燃燒過程示意圖Fig.1 Scheme of classic propellant burning

燃燒反應區前沿主要通過熱傳導和分子擴散引燃未反應火藥，未反應火藥進入反應區后通過化學反應速率控制反應程度，反應完全后進入反應產物區。因此，燃燒反應區寬度可以由宏觀傳質過程和微觀反應過程決定。基于以上分析結論，本文將火藥燃燒模型劃分為未反應狀態方程、宏觀燃速方程、微觀反應速率方程和反應產物方程；火藥燃燒通過宏觀燃速控制燃燒波前沿速度，即不同位置火藥的起燃時間，然后通過微觀反應速率方程控制起燃火藥的化學反應速度，從而唯象地描述火藥燃燒反應區現象。

宏觀燃速方程主要是建立燃速與壓力的指數關系，此方程源于經典的火藥幾何燃燒模型。

u=BPn

(1)

微觀反應速率方程主要是建立反應速率與壓力的關系，此方程源于炸藥多項式反應速率方程。

(2)

反應產物狀態方程主要是采用范德瓦爾斯氣體狀態方程，用以描述高壓下反應產物的壓力變化。

(3)

式中,u為宏觀燃速，P為燃氣壓力，ψ為燃燒分數，R為氣體常數，T為燃氣溫度，V為比容，ρs為火藥密度，A，B，R1，R2，n為常數。以上3個方程聯立，可以描述火藥經歷化學反應生成反應產物的過程。

2 火藥燃燒模型參數擬合

火藥燃燒模型涉及的參數較多，且部分參數并無物理意義，因此，確定模型參數是準確描述火藥燃燒特性的前提。常用的試驗方法一般采用密閉爆發器測壓，即在一個已知容積的密閉容器內測定一定質量火藥燃燒產生的壓力曲線，然后采用火藥燃燒模型進行仿真計算，將計算結果與試驗結果進行反復擬合，最終確定火藥燃燒模型的參數。

典型的密閉爆發器試驗示意圖如圖2所示。試驗裝置由點火器、主裝藥、密閉容器和壓電傳感器組成。當點火器接收到電信號后，點火器起爆主裝藥，主裝藥燃燒產生高溫高壓燃氣，通過壓電傳感器記錄密閉容器內壓力時間變化曲線。試驗中，密閉爆發器容腔為10 ml，采用兩個壓電傳感器記錄壓力變化曲線，點火器10 ml容腔的輸出壓力在10 MPa左右，被測主裝藥為SL17雙基推進劑。

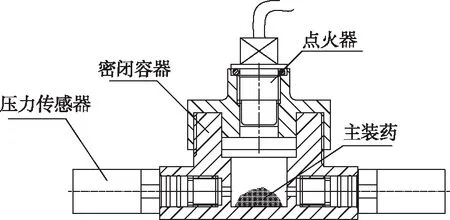
圖2 密閉爆發器試驗裝置示意圖Fig.2 Geometry of closed vessel test

根據密閉爆發器結構，建立了其計算模型，如圖3所示。計算模型對物理模型進行了簡化，僅考慮空氣域和火藥，點火器通過定義能量入口來模擬。計算中，能量入口以壓力形式向容腔內注入一定壓力，當壓力達到一定值時，火藥被引燃，火藥不斷燃燒導致容腔內壓力逐漸增大，直至火藥燃燒完畢，計算過程中考慮壁面散熱影響。

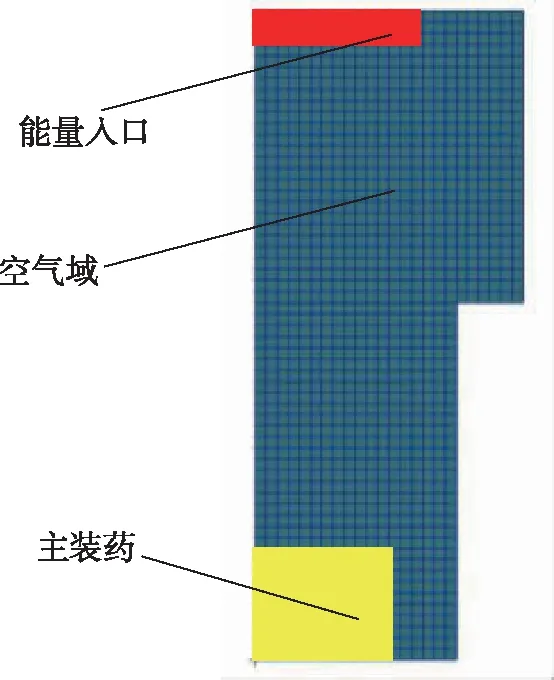
圖3 密閉爆發器計算模型圖Fig.3 Numerical model of closed vessel

3 模型驗證

為了驗證火藥燃燒模型及參數的準確性，建立彈射器計算模型，對彈射器工作過程進行數值模擬計算，獲得彈射器彈射速度，并且與試驗結果進行比較，驗證計算準確性。

彈射器結構示意圖如圖4所示。彈射器主要由外筒、內筒、活塞、滑桿、火藥、點火器和剪切銷組成。點火器接到電信號后引爆，點火器火焰起爆主裝藥，主裝藥燃燒產生高壓燃氣，當燃氣壓力達到一定值時內筒剪斷剪切銷開始運動，最終以一定速度飛出外筒。根據裝置物理模型，建立彈射器計算模型，計算模型對物理模型進行了簡化，點火器通過能量入口實現，剪切銷通過在內外筒之間設置連接力實現。模型中內筒、外筒、活塞和滑桿材料均為鋼，采用彈塑性材料模型描述；火藥為SL17，藥量為100 mg，采用火藥燃燒模型描述，剪切銷連接力為2 000 N。彈射器計算模型圖如圖5所示。

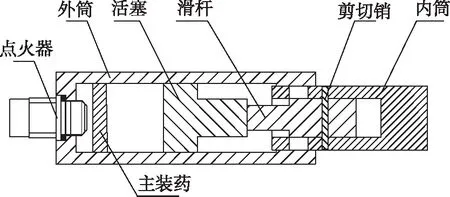
圖4 彈射器結構示意圖Fig.4 Geometry of the catapult

圖5 彈射器計算模型Fig.5 Numerical model of the catapult

4 計算結果與分析

4.1 SL17模型參數

SL17火藥參數擬合的基本過程為：首先輸入一組火藥燃燒模型參數進行模擬計算，將計算獲得的壓力曲線與試驗結果進行比較，根據比較結果調節相應參數，再次帶入模型進行計算，反復調節，直至模擬結果與試驗結果基本吻合，最后確定的一組參數可以用來描述SL17火藥的反應過程。

密閉爆發器計算過程中壓力云圖如圖6所示。從圖6中可以看出，在燃燒開始后1.5 ms時，容腔內最大壓力為38 MPa，最小壓力為37.3 MPa，表明容腔內壓力均勻性較好，燃燒產生的燃氣有足夠的時間在容腔內擴散，可以將容腔內氣體作為均壓狀態，因此，容腔內各位置的壓力變化歷程基本相同。在容腔內任意選擇一點監測壓力變化過程，將計算結果與試驗結果進行對比，如圖7所示。從圖中可以看出，試驗曲線的初始階段，壓力在短時間內有一個突躍，這是點火器起爆后引起容腔內壓力迅速增加，突躍后壓力曲線緩慢上升，表明火藥開始燃燒；在2.2 ms時，容腔內壓力達到峰值55 MPa，此后，容腔內壓力基本維持恒定，表明火藥燃燒完全。因此壓力曲線可以分為兩段，初始壓力突躍段為點火器燃氣壓力輸出段，突躍段之后壓力上升段為火藥燃燒燃氣壓力輸出段。由試驗曲線與計算曲線對比看出，只是在初始段兩條曲線有一定差別，在火藥燃燒段兩者吻合性較好。這是由于點火器的輸出特性與模型中簡化的能量入口有一定差別，能量入口的輸出速率較低，而點火器輸出速率較快。總體而言，模型對火藥燃燒段的計算結果與試驗結果吻合性較好，表明模型可以很好地反映火藥的燃燒特性，最后擬合得到了SL17火藥的模型參數，如表1所示。

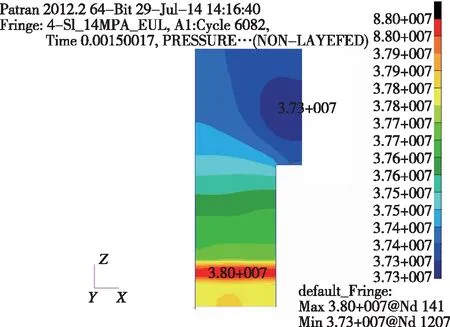
圖6 計算過程中壓力云圖Fig.6 The calculation pressure contour

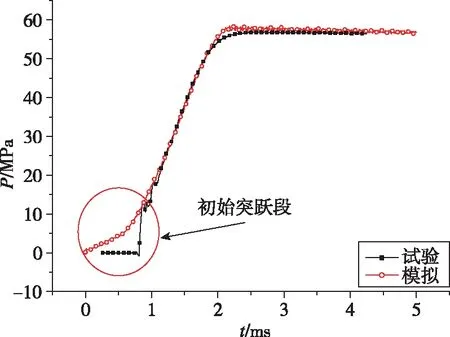
圖7 計算曲線與試驗曲線對比Fig.7 Comparison between calculation and test curve

表1 模型參數表Tab.1 Model parameters of SL17

4.2 彈射器工作過程計算

將擬合得到的參數代入彈射器計算模型進行計算，驗證模型及參數的準確性。不同時刻彈射器運動過程如圖8所示。從圖8中可知，0.17 ms時，容腔內的火藥開始燃燒，容腔內壓力開始升高，此時容腔內最大壓力為5 MPa左右，火藥燃氣對活塞的推力仍小于剪切銷剪切力，因此活塞并未開始運動；隨著火藥燃燒量的增加，容腔內壓力逐漸增大，當某一時刻，容腔內壓力大于剪切銷剪切力時，剪切銷被剪斷，活塞開始推動滑桿運動；在1.03 ms時，活塞與滑桿組合體撞擊內筒，此時容腔內最大壓力在11 MPa左右，此后活塞、滑桿和內筒的組合體開始一起加速運動；在1.29 ms時，活塞與外筒限位臺階碰撞，活塞停止運動，內筒和滑桿組合體在慣性作用下繼續向前運動，此時容腔內最大壓力為9.2 MPa，容腔內壓力已經開始降低；在1.34 ms時，內筒與滑桿組合體和彈射器本體分離，內筒和滑桿以一定速度飛出外筒，容腔內壓力下降至9 MPa。從以上計算過程可以看出，整個計算模型完整反映了彈射器的彈射分離過程；當彈射器容腔較小時，容腔內火藥燃燒產生的壓力均一性較好；隨著容腔的增大，容腔內燃氣壓力有一定梯度分布，最大壓強與最小壓強相差2 MPa左右，且火藥位置的壓強高于活塞尾部壓強。

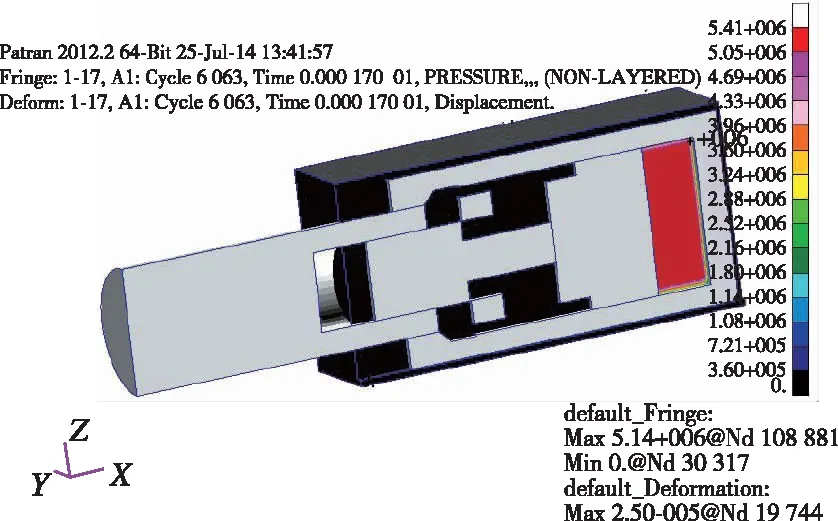
(a) 0.17 ms

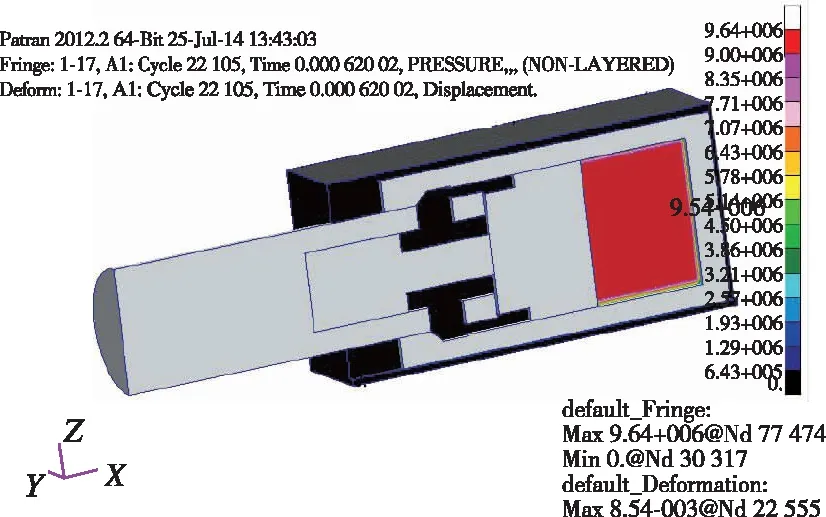
(b) 0.62 ms

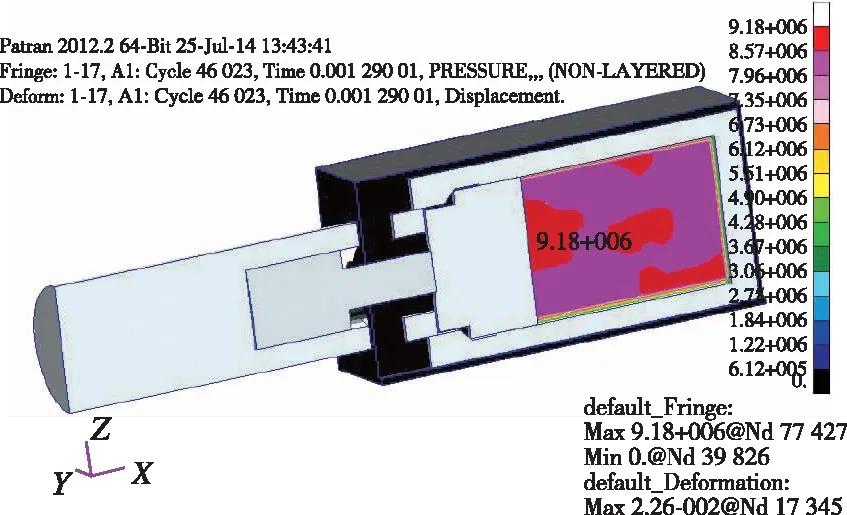
(c) 1.29 ms

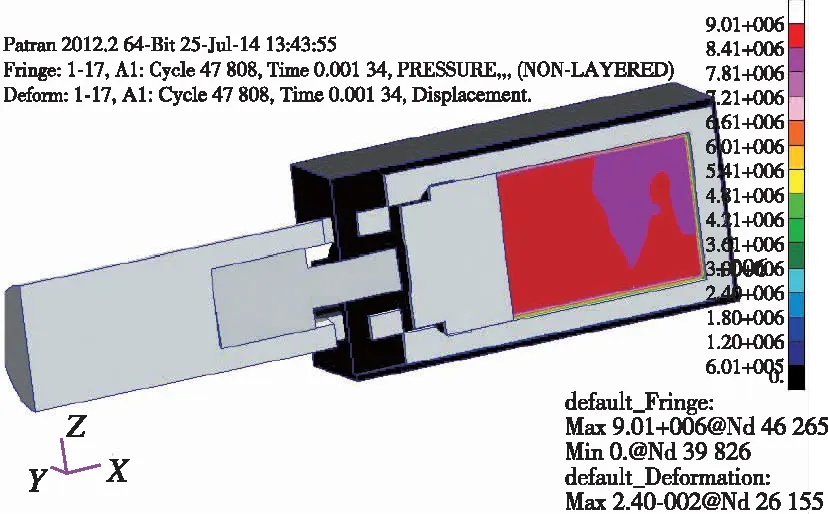
(d) 1.34 ms圖8 彈射器運動過程圖Fig.8 The movement process of catapult at different moments

彈射器工作的主要性能指標為彈射速度，因此，通過彈射速度可以驗證計算準確性。計算過程內筒速度曲線如圖9所示。由圖9中可知，內筒速度呈階梯狀增加，在0.6 ms時，活塞和滑桿組合體與內筒碰撞，將內筒速度迅速增加到17 m/s左右；此后，內筒速度出現一個平臺，通過運動過程分析表明，這是由于碰撞后滑桿和活塞組合體速度降低，而內筒速度提高，導致滑桿和活塞組合體與內筒出現短暫分離；在0.9 ms左右，活塞和滑桿組合體在燃氣壓力作用下，再次與內筒發生碰撞，內筒速度進一步提高至25 m/s左右，然后又進入速度恒定段，組合體與內筒再次分離；依次循環，經過4次碰撞后，活塞被限位在外筒內，滑桿無法繼續加速內筒，最終內筒和滑桿的組合體以35 m/s左右的速度飛出外筒。

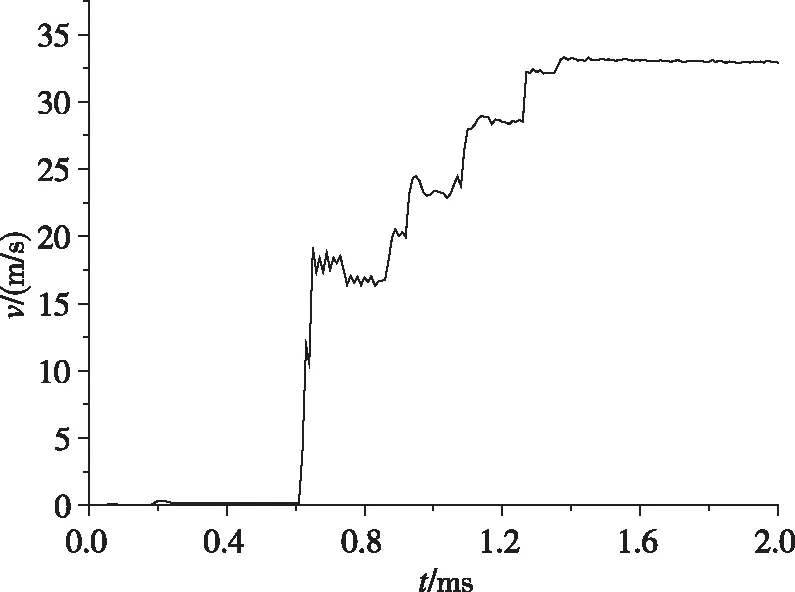
圖9 計算過程內筒速度曲線Fig.9 Calculation velocity-time curve

試驗測量內筒速度曲線如圖10所示。由圖10可知，試驗測量的曲線相對平滑，這是由于測量設備采樣頻率僅有4 000 Hz，而內筒由開始運動到最大速度只有1 ms左右，因此，該試驗測量并不能反映內筒加速過程的細節。最終，內筒達到的最大速度在40 m/s左右，而計算得到的最大速度在35 m/s左右，計算結果與試驗結果誤差在10%左右。考慮到計算模型對彈射器產品進行了較大簡化，并且對點火器能量輸出的描述有一定偏差，可以認為該計算結果與試驗結果吻合性較好，因此火藥燃燒模型和參數能夠較好地描述彈射器工作過程。

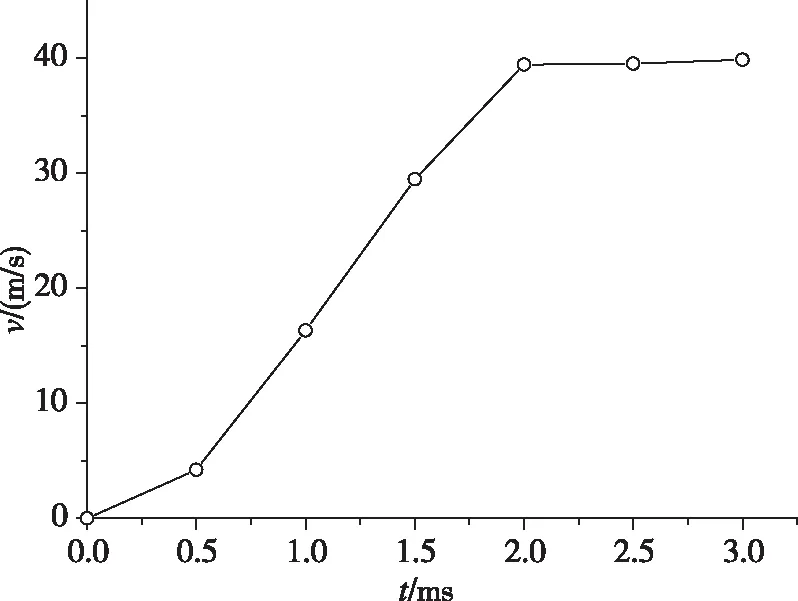
圖10 試驗測量內筒速度曲線Fig.10 Test velocity-time curve

5 結論

火藥燃燒過程是一個復雜的物理化學過程，準確描述火藥燃燒過程是進行火工裝置工作過程數值模擬計算的關鍵。本文借鑒炸藥反應的多項式模型，建立了火藥燃燒單項式數學模型，模型由未反應狀態方程、宏觀燃速方程、微觀反應速率方程和燃氣狀態方程組成；通過密閉爆發器試驗數據擬合了SL17火藥燃燒模型參數，并且對彈射器工作過程進行數值模擬計算，用以驗證模型及參數的準確性。結果表明，密閉爆發器試驗結果可以用于擬合火藥燃燒模型參數；采用該模型和參數計算的彈射器運動過程可以完整反映彈射器彈射分離過程；計算得到的彈射分離速度與試驗測量值吻合性較好，表明火藥燃燒模型可以用于火工裝置工作過程仿真計算。