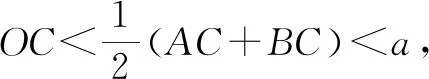基于思維能力培養的一節課堂教學評析
——從“正多邊形與圓”談起
?江蘇省泰州市姜堰區張甸初級中學 王雨霞
在“正多邊形與圓”這一章節的教學中,常常會出現這樣的現象:學生能理解正多邊形與圓的關系,但是在解決具體問題的時候,總是不得其法.因此大多教師就采取刷題的方式,以增加學生的解題體驗,期望讓他們識記更多的題目,進而提升數學成績.事實上,這樣的培養方式不利于學生的可持續發展.教師要關注學生的思維品質,要讓他們具備一定的高階思維能力,比如創新能力、推理能力等,進而能以一題應萬題,既提升數學素養又減輕學業負擔.
1 創設問題情境,激活數學思維
教師在教學的過程中要設置一定的問題,促使學生進入思考狀態,不再游離于教師所講述的知識點之外.教師設置的問題要在一定的情境中進行,這樣才能使學生對提出的問題有更感性、更直觀的認識,進而也能找尋到相應的解決方法.事實上,將問題與情境對接能讓學生的多元感官參與到思考中,思維的火花也逐漸被激活.以下面的探究活動為例.
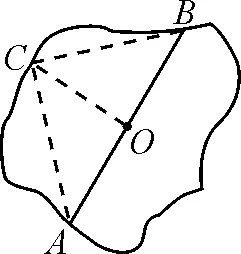
學生在小組合作討論一團周長為4a的線圈時,發現了如下兩個命題:如圖1所示,當線圈做成正三角形ABC時,能被半徑為a的圓形紙片完全蓋住;如圖2所示,當線圈做成正方形ABCD時,能被半徑為a的圓形紙片完全蓋住.
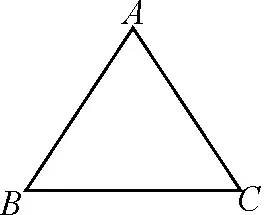
圖1

圖2
教師追問:對于圖1、圖2所展示的兩個命題,能不能再想出一個命題呢?學生遇到的情境是兩幅圖以及圖中所呈現的命題,學生要解決的問題是創設新的問題.有了情境,學生會覺得問題更容易解決.他們發現“能被半徑為a的圓形紙片完全蓋住”是以上兩個命題共有的結論,不同的是線圈做成的圖形發生了變化,由原先的三角形變成了正方形.因此,有學生就想出這樣的命題:將線圈做成平行四邊形ABCD時,能被半徑為a的圓形紙片完全蓋住.
學生作出如圖3所示的平行四邊形ABCD,再連接AC,BD交于點O.由條件OB+OD 圖3 在數學教學的過程中,教師要培養學生的思維能力,就要讓學生順著問題繼續思考,以提升他們的創新能力.當前的數學教學中,學生更多的時候只是在被動地完成教師布置的題目,題目做完了,思考也就結束了.其實教師要培養學生深度學習的能力,要讓學生的思維持續發展,以探究出更多的數學奧秘. 圖4 要激發學生的思維就要為學生提供更多的體驗機會,在體驗中學生的能力會得到多方面的生長.給學生體驗的機會,其實就是給他們運用所學認知解決實際問題的機會.當前的數學教學中,存在著學生解決實際問題的能力不強的現象.這主要有兩個方面的原因,一是教師在教學中沒能將生活中的問題引入課堂,二是學生沒能主動將實際問題與課堂認知對接.因此,教學中教師要關注生活中的問題,以提升學生的數學思維. 還以圖3展現的命題為例,學生提出了一個值得思考的問題:生活中見到的圖形大多是任意的,如果當線圈做成任意形狀的圖形時,是否還能被半徑為a的圓形紙片完全蓋住?學生的思考已經突破了課堂所給的基本圖形的范圍,他們將生活中隨處可見的不規則圖形帶入課堂,同時想發現這些不規則圖形之中是否蘊含著一些規律.思維跳出原有的框架,進入新的場域. 圖5 總之,在數學教學的過程中,教師要關注學生的思維生長,給他們適切的土壤,讓他們開出美麗的思維之花.教師要培養學生的思維能力,真正落實數學教學的主要目標,進而促進學生的全面發展.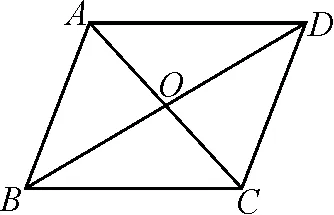
2 創新問題設計,促發數學思維
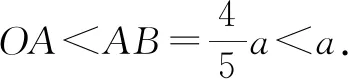
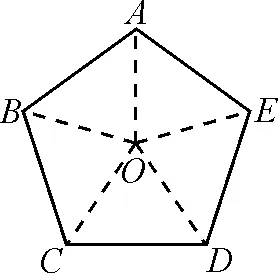
3 解決實際問題,提升數學思維