初中數(shù)學“問題引領(lǐng)課堂”的實踐與思考

?甘肅省玉門市第三中學 張宏亮

在初中數(shù)學的傳統(tǒng)課堂教學模式中，問題主要作為一種銜接機制，用于推進教學進程、檢驗教學成果[1].如何最大程度發(fā)揮數(shù)學問題的價值，是值得數(shù)學教師探究的學術(shù)問題.通過建構(gòu)“問題引領(lǐng)課堂”，即圍繞數(shù)學問題建立全過程教學途徑，可有效拓展數(shù)學問題價值、優(yōu)化教學質(zhì)效.

1 初中數(shù)學“問題引領(lǐng)課堂”的實踐原則

1.1 導向性原則

所謂導向性，是指“問題引領(lǐng)課堂”必須具備清晰的教學目標.一方面，在數(shù)學問題的設計過程中，既要確保問題與當前教學內(nèi)容高度契合，實現(xiàn)數(shù)學知識的多元化展現(xiàn)、多維度運用，也要突出學生的主體地位，確保所提出的問題具有探索空間.另一方面，要始終堅持數(shù)學核心素養(yǎng)的培養(yǎng)，不能將“問題”作為數(shù)學答案的“容器”，而是學生數(shù)學能力、思維、意識及創(chuàng)新的“觸發(fā)機制”.

1.2 可行性原則

所謂可行性，是指在圍繞著數(shù)學問題創(chuàng)設情境、提供資源、組織學習等實踐中，不能超過學生當前數(shù)學認知水平的最大限度[2]，或者從教師角度出發(fā)，所設計的問題應處在合理的知識體系之內(nèi)，如“勾股定理”教學的過程中，不應該摻雜尚未講授的“平面直角坐標系”思維和方法.同時，可行性原則適用范圍很廣，并不局限于教學內(nèi)容的適應性，例如在“教學評價”的標準、方式上，也應該契合當前初中數(shù)學課堂環(huán)境與需求，即評價內(nèi)容限定于課堂之內(nèi).

1.3 發(fā)展性原則

不同于傳統(tǒng)意義上的初中數(shù)學課堂問題，能夠“引領(lǐng)課堂”的問題，應該注重對學生發(fā)展性能力的培養(yǎng)，讓學生通過一個或一組數(shù)學問題，進行自我診斷，激勵學習行為，定位數(shù)學水平，以及從低階思維水平不斷向高階思維水平發(fā)展.所以，初中數(shù)學“問題引領(lǐng)課堂”在實踐過程中，問題不應該始終保持靜態(tài)，可通過題面變化、一題多解、同類歸一等方式，豐富問題本身的表現(xiàn)形式，避免學生數(shù)學思維出現(xiàn)僵化、慣性的桎梏.

1.4 生本性原則

所謂生本性，簡單地說就是“以學生為主體、為中心”，避免學生成為“知識容器”，陷入被動學習、機械解題的狀態(tài).因此，初中數(shù)學問題設計之初，要考慮能否激起學生的求知欲，能否引導學生展開思考；相對應地，教師必須綜合布局一個數(shù)學問題的情境預設、延伸發(fā)展、可逆向性等，讓學生在固有數(shù)學知識及生活經(jīng)驗的基石之上，順利地跨過最近發(fā)展區(qū).例如，將同一個問題進行拆分，形成由易到難、不斷發(fā)展的提問形式.

2 初中數(shù)學“問題引領(lǐng)課堂”的實踐策略

立足初中數(shù)學課程，所謂“問題引領(lǐng)課堂”的主張，就是“以數(shù)學問題為媒介貫穿整個數(shù)學課堂全過程”的教學組織方式.具體實踐策略主要有以下四種.

2.1 創(chuàng)設情境，具象導入

圍繞數(shù)學問題創(chuàng)設情境，可以實現(xiàn)抽象→具象的有效轉(zhuǎn)化，借此調(diào)動學生的生活經(jīng)驗、增強直觀想象能力，通過這樣的“情境式問題”引領(lǐng)課堂，有助于學生數(shù)學思維在抽象性、具象性之間有效切換，也為數(shù)學課堂平添了一份樂趣，引導學生逐步進入深度學習狀態(tài).

例如，北師大版八年級(下)關(guān)于“圖形的旋轉(zhuǎn)”的教學中，教師圍繞“五角星”圖案提出如下問題：(1)五角星圖案的特征有哪些？(2)記五角星中心點為O，旋轉(zhuǎn)多少度圖案會出現(xiàn)重合現(xiàn)象？(3)五角星旋轉(zhuǎn)360°的過程中，圖案會出現(xiàn)幾次重合？以上問題采取純語言描述的形式呈現(xiàn)，對于想象能力強的學生來說，要理解題面并非難事，但對于空間感薄弱、理解能力差的學生，則難以自主建構(gòu)五角星的旋轉(zhuǎn)軌跡、運動規(guī)律.事實上，在問題引領(lǐng)之前，先利用多媒體展現(xiàn)五角星旋轉(zhuǎn)動畫，創(chuàng)建一個直觀、具象的問題情境，能夠很好地規(guī)避此類問題.從這個角度說，圍繞數(shù)學問題創(chuàng)設情境，本質(zhì)上是提供了一種“雙編碼”(即數(shù)學元素的靜態(tài)編碼、動態(tài)編碼)的解構(gòu)及解讀途徑，便于學生全面深入地理解問題.

2.2 問題分層，適應差異

客觀上，以問題引領(lǐng)開展數(shù)學課堂活動，勢必要考慮學生數(shù)學水平差異，兼顧數(shù)學問題在各個層次均能發(fā)揮引導價值[3].所以，“問題分層、適應差異”是初中數(shù)學課堂教學的一項重要舉措，其實踐策略并不復雜，可在一節(jié)課的鞏固環(huán)節(jié)和專門的練習課上，提出具有層次性的問題；層次性問題設計遵循同一范圍、由易到難的原則，即在相同的數(shù)學知識范圍之內(nèi)，逐漸增加問題中包含的知識點.

例如，北師大版八年級(上)第六章數(shù)據(jù)的分析“回顧與思考”教學中，教師通過兩組數(shù)據(jù)提出如下問題：(1)兩組數(shù)據(jù)中，哪一組的平均數(shù)較大？(2)兩組數(shù)據(jù)中，哪一組的平均數(shù)最接近中位數(shù)？(3)兩組數(shù)據(jù)的眾數(shù)與中位數(shù)各相差多少？(4)判斷兩組數(shù)據(jù)的離散程度.以上四個問題所涉及的知識點是同一章的內(nèi)容，彼此之間存在密切的聯(lián)系，在兩組數(shù)據(jù)固定的情況下，依次增加求解難度，這一過程可以有效檢驗學生哪些知識掌握牢固、哪些知識欠缺.

2.3 同類歸一，探尋規(guī)律

數(shù)學是對客觀世界的抽象轉(zhuǎn)化4].很多問題看似復雜，一旦抽離“非數(shù)學要素”的表述部分，實質(zhì)上屬于同一類問題.“同類歸一”問題引領(lǐng)數(shù)學課堂的方式，與“創(chuàng)設問題情境”引領(lǐng)課堂的方式恰恰相反，它是一種將現(xiàn)實問題抽象為數(shù)學符號的表達形式，如以下兩個問題.

問題1如圖1所示，假如從一點出發(fā)有n條射線，如何表達角的數(shù)量？

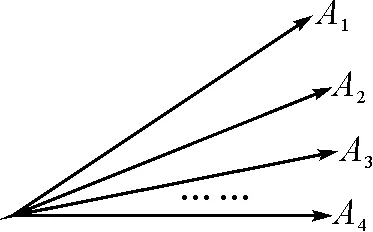
圖1

問題2學校以班級為單位組織拔河比賽，假如有n個班，一共要進行多少輪比賽？

2.4 變式訓練，一題多解

以數(shù)學問題引領(lǐng)數(shù)學課堂的最終目的，是讓學生靈活運用數(shù)學知識解決問題[5].變式訓練可以從不同的角度出發(fā)，將數(shù)學知識的價值展現(xiàn)出來.例如，北師大版初中數(shù)學(七下)第84頁的“想一想”.如圖2，AB與CD相交于點O，O是AB的中點，∠A=∠B，△AOC與△BOD全等嗎？為什么？

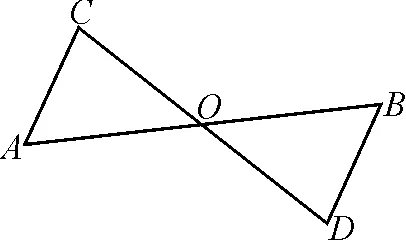
圖2

以上問題直接利用“角邊角”(ASA)判定定理即可得出結(jié)論.然而，判斷兩個三角形全等的定理并不唯一，還包括“邊邊邊”(SSS)、“邊角邊”(SAS)、“角角邊”(AAS)，教師在講解這一問題時，可以展開一定的變式訓練.例如，將“O是AB的中點”替換為“AC=BD”，或者將“O是AB對中點”延伸為“O是AB，CD的中點”，題面發(fā)生了變化，所用到的知識也相應地發(fā)生了變化、解法也變得多樣，能夠很好地引領(lǐng)數(shù)學課堂多角度發(fā)展.

3 總結(jié)與思考

綜上所述，本文從宏觀上闡述了“問題引領(lǐng)課堂”的建構(gòu)原則，并在相對促狹的初中數(shù)學課堂空間內(nèi)，對問題實踐方式進行了一系列創(chuàng)新.創(chuàng)新點主要體現(xiàn)在賦予問題“張力”及問題講解的“拓撲性”上，即一個問題可以被拆分，多個問題也可以被歸一，其目的是讓學生更深刻地了解數(shù)學知識原理與應用特點，而非僅僅求出正確答案.