高速公路合流區沖突極值建模與交通事故預測

鄭 來，侯芹忠，郭延永，楊曉冬

(1. 哈爾濱工業大學 交通科學與工程學院, 黑龍江 哈爾濱 150090；2. 哈爾濱工業大學(威海) 汽車工程學院，山東 威海 264209；3. 東南大學 交通學院，江蘇 南京 210096；4. 哈爾濱職業技術學院, 黑龍江 哈爾濱 150081)

0 引言

合流區是高速公路的重要組成部分，同時也是高速公路運行安全的薄弱環節。車輛合流過程中，駕駛員需進行加速、選擇可接受間隙、變道等一系列復雜操作，容易出現操作不當從而引發交通事故。統計表明，合流區交通事故占高速公路事故總數的比例一直居高不下，約為高速公路基本路段交通事故的4～6倍[1-2]。

在對高速公路合流區交通安全的研究中，交通沖突技術得到了越來越多的應用。交通沖突是指車輛在時間和空間上相互接近至一定程度，以至于若不改變其運動狀態，就會發生碰撞的交通事件[3]。車輛合流過程中會出現較為頻繁的側向沖突和追尾沖突，可為開展高速公路合流區交通安全研究提供比交通事故更為充足的數據支撐。為了識別合流區的交通沖突，學者們多采用后侵入時間(Post Encroachment Time, PET)作為沖突嚴重程度的衡量指標，通過選取合適的后侵入時間閾值界定交通沖突，進而通過沖突數(率)分析高速公路合流區的安全性[4-6]。相關研究發現，交通流量、沖突車輛速度差、加速車道長度、重型車比例等因素對合流區交通沖突有顯著影響[5-9]。

雖然交通沖突技術為高速公路合流區交通安全研究提供了新的手段，但交通沖突作為合流區安全分析指標的有效性尚未被充分證明[10]。本研究旨在通過極值理論建立合流區沖突與交通事故之間的關系模型，在驗證交通沖突技術有效性的基礎上更好地開展高速公路合流區交通安全研究。極值理論作為一種分析極小概率事件分布的理論，能夠通過短時段內常見事件(如降水量、交通沖突)發生的概率外推長時段內罕見極值事件(如洪水、交通事故)發生的概率，已被應用于交叉口沖突-事故關系研究[11-13]、高速公路基本路段沖突-事故關系研究[14-15]、高速公路合流區沖突-事故關系研究[16]。然而，已有研究主要針對單個研究對象分別建立沖突極值統計模型，雖然證明了該模型在交通事故預測方面的可行性，但都存在單個研究對象沖突極值樣本數量較少的問題，在很大程度上影響了事故預測精度。比如，Zheng等[16]針對15個高速公路合流區分別構建了沖突極值統計模型，研究發現模型預測事故數與觀測事故數的誤差最高可達55.9次/a。

為了解決單個合流區沖突樣本數量有限的問題，也為了更有效地利用合流區交通沖突預測交通事故，本研究將結合貝葉斯層級超閾值理論，構建能融合多個合流區沖突數據的極值統計模型并據此預測合流區交通事故，以期拓展交通沖突極值統計建模的方法體系，也為基于交通沖突的高速公路合流區交通安全研究提供新思路。

1 合流區交通沖突判別

1.1 數據采集與處理

本研究共采集了7個高速公路合流區的交通運行數據，分別為葫蘆島、綏中、興城、高升、五龍背、通遠堡和本溪。前4個合流區來自于沈山(沈陽至山海關)高速公路，雙向8車道，設計速度為120 km/h；后3個合流區來自于沈丹(沈陽至丹東)高速公路，雙向4車道，設計速度為100 km/h。

數據采集采用錄像法，共采集了白天晴好天氣情況下53 h的視頻。其中，葫蘆島、興城、本溪的視頻時長均為7 h，其他4個合流區的視頻時長均為8 h。基于錄制的視頻，采用人工觀測法進行了分車道、分車型的交通流量統計，具體結果見表1。

表1 交通流量與合流沖突統計情況一覽表

交通事故數據來自于沈山高速和沈丹高速的路政管理部門，時間跨度為2010年1月至2012年12月，該時段與視頻采集時間相近，且在2010—2013年間所調查合流區的道路、交通、環境條件無顯著變化。基于事故發生時間、地點樁號、上下行方向等信息，得到了合流區影響范圍內白天時段的交通事故，共54次，具體見表1。

1.2 合流沖突判別

高速公路合流區的合流車輛主要影響主線最外側兩車道的交通運行[4]。因此，本研究重點關注合流車輛與主線最右側兩車道上車輛間的交通沖突。交通沖突嚴重程度衡量指標選用后侵入時間(PET)，即后車頭部到達沖突區域的時間與前車尾部離開沖突區域的時間差[3]。

合流過程中的PET是指跟隨車輛的頭部到達侵入線的時間與先導車輛的尾部離開侵入線的時間之差，其中一輛車為合流車輛。侵入線指垂直于車道分界線并經過車道分界線與車輛變道軌跡交點的虛擬直線[17]。PET的具體測量如圖1所示，合流過程中，合流車輛(S)可能與每條車道上的前車(L)和后車(F)產生交通沖突，因此，每一輛合流車輛最多可測出4個PET值，為了保證極值樣本的獨立性，本研究選取其中的最小值作為該合流行為的PET。實際測量利用VirtualDub軟件逐幀播放視頻并計算PET，測量精度為0.04 s(每25幀為1 s)。

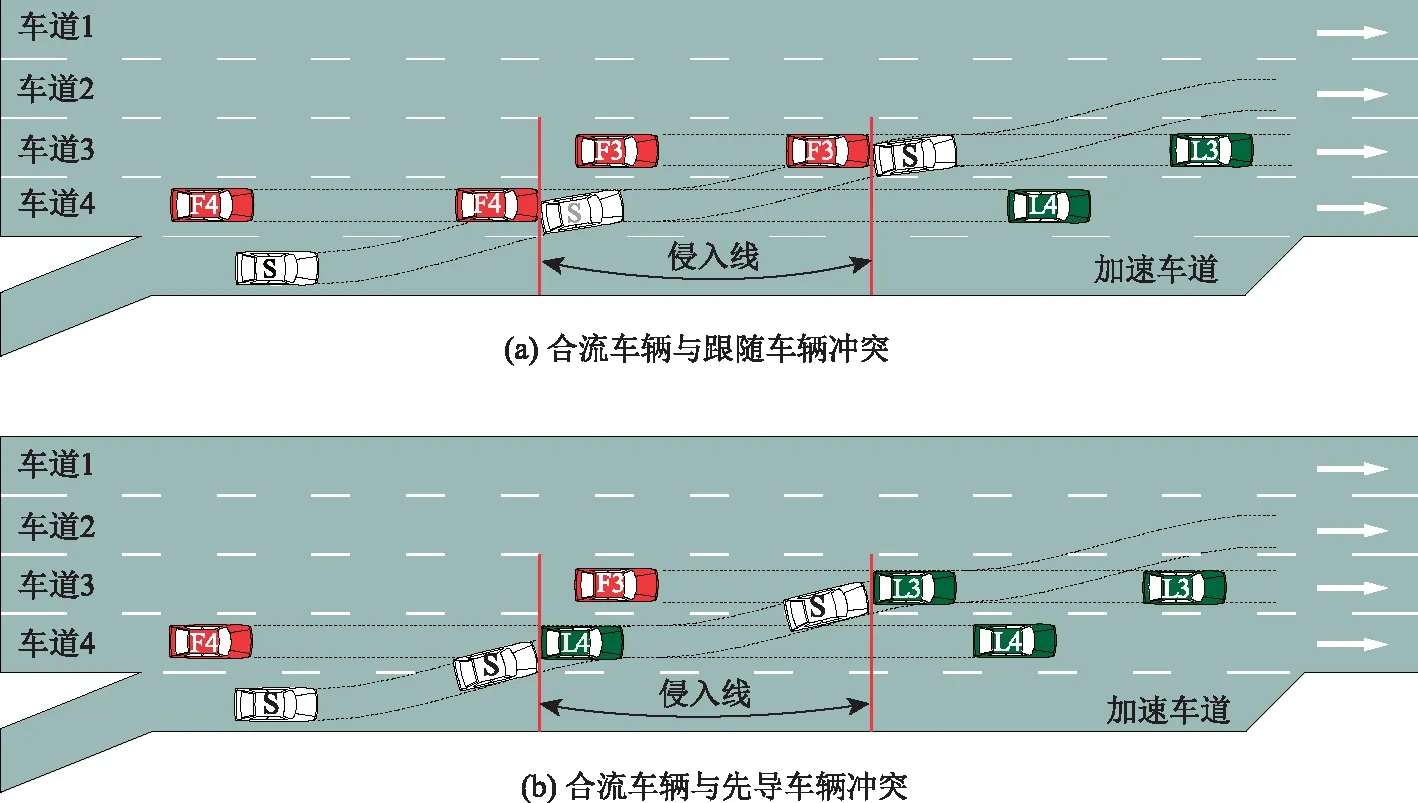
圖1 合流沖突PET測量示意圖

由于部分車輛合流時，視頻視野范圍內主線上并未出現其他車輛，故此時不存在合流沖突。最后，共識別得到合流沖突898次，其中PET最小值為0.20 s、最大值為11.24 s。各合流區的沖突次數及對應PET均值見表1。

2 基于沖突極值模型的事故預測

交通沖突與交通事故具有過程相似性，并且交通事故可視為交通沖突的極值事件，即時空接近度趨近于0的交通沖突為交通事故。因此，可通過沖突極值建模外推交通事故發生的概率。本研究以超閾值極值理論為基礎構建沖突極值模型并預測交通事故。

2.1 貝葉斯層級超閾值極值模型

2.1.1 超閾值極值模型

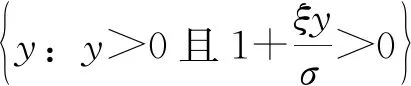
(1)

式中，G(y)為GPD分布；σ>0，為尺度參數；ξ為形狀參數。

2.1.2 貝葉斯層級結構

為了表征沖突極值的非穩態特性，在超閾值極值模型的基礎上引入貝葉斯層級結構，將影響沖突極值的相關因素融入模型中。層級模型包括數據層、過程層和先驗知識層。其中，數據層采用超閾值模型對沖突極值進行建模，其形式如下：

(2)

式中，G(yik|φik,ξik)為廣義極值分布；yik為合流區i上的第k個極值(i=1,…,s；k=1,…,ni；其中s為合流區數量，ni為第i個合流區上的沖突極值個數)；σik和ξik分別為GPD的尺度參數和形狀參數。過程層則是利用潛高斯過程將GPD模型參數與影響沖突極值的變量進行關聯，關聯函數選用恒等關聯函數，具體如下：

(3)

式中，φik=logσik,為變換后的尺度參數，以保證尺度參數的非負性；αφ0和αξ0分別為尺度參數和形狀參數的常數項；X為影響沖突極值非穩態特性的協變量集合，為向量；αφ為對應的參數向量；εφi和εξi分別為各合流區尺度參數和形狀參數的隨機誤差項，以表征各合流區未觀測因素導致的沖突極值異質性。需要說明的是，由于超閾值極值模型對形狀參數的敏感性以及形狀參數精準估計的難度，一般不考慮相關變量對形狀參數的影響[18]。將常數項和隨機誤差項結合，簡化得到隨機截距過程層模型：

(4)

式中，αφ0i和αξ0i分別為合流區i的形狀參數和尺度參數常數項。

先驗層為過程層模型參數分配先驗分布。假設所有模型參數相互獨立，由于現階段沒有可靠的先驗信息，所以參數αφ0i和αφ均采用無信息先驗概率分布，具體為采用0均值大方差的正態分布作為其先驗分布，即αφ0i，αφ～N(0,106)。同樣，由于超閾值極值模型對其形狀參數的敏感性，不恰當的先驗分布容易導致模型不收斂，所以借鑒了已有沖突極值模型研究中有關形狀參數的先驗信息。在已有研究中，估計得到的形狀參數均位于(-1, 1)之間[11, 13]，因此本研究選用均勻分布作為其先驗分布，即αξ0i～N(0, 0.25)。

2.2 閾值選取方法

超閾值模型構建首先需要確定合理的閾值u，才能估計參數σ和ξ。如果閾值選取不合理，將會導致錯誤的模型估計。常用的閾值選取方法包括平均剩余壽命圖及閾值穩定性分析圖等圖解方法和均方差法等數值方法[18]，然而這些方法所確定的均為穩態閾值，并未考慮外在因素對閾值的影響。為克服這一缺陷，本研究選用分位數回歸方法確定閾值[19]。從直觀上看，高分位數對應的閾值一般都能保證所對應的超閾值樣本服從GPD分布。

分位數回歸模型的具體形式如下：

Q(τ|X)=X′τβτ,

(5)

式中，τ∈(0,1),為分位數；Q(τ|X)為分位數τ對應的因變量值(即qτ)；Xτ為影響閾值非穩態特性的協變量集合為向量；βτ為參數向量。分位數回歸模型參數的標定可通過求解式(6)所示的優化問題解決：

(6)

式中，x′τβτ為式(5)向量集合中的一個變量。

在分位數回歸確定的閾值基礎上，進一步采用閾值穩定性分析圖驗證所選取分位數的合理性。該方法的基本原理為：如果超出閾值u0的樣本服從GPD(σ0,ξ)，則對任意閾值u>u0，其閾值u超出值同樣服從GPD(σu,ξ)，且GPD對應的修訂后的尺度參數σu和形狀參數ξ在理論上是恒定不變的，其中：

σu=σ0+ξ(u-u0)，

(7)

式中，σ0為超出閾值u0的GPD分布的尺度參數。

2.3 模型求解與比選

采用貝葉斯方法對貝葉斯層級超閾值極值模型進行估計。在確定閾值、模型結構和先驗分布的基礎上，模型參數集合θ(向量)的后驗概率密度函數為：

(8)

式中，Y為輸入數據集合，為向量；p1,p2,p3分別為數據層，過程層和先驗層的概率密度函數，由參數θj(j=1,2)決定，其中θ1=[φ,ξ]T，θ2=[αφ0,αφ,αξ0]T。p1，p2，p3的具體計算公式如下：

(9)

(10)

p3(θ2)=pαφ0(αφ0)×pαφ(αφ)×pαξ0(αξ0),

(11)

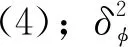
在具體構建貝葉斯層級沖突極值模型時，考慮不同變量對沖突極值的影響，即將不同變量引入式(4)可形成一系列模型。最優模型的選取采用方差信息準則(Deviance Information Criterion, DIC)[20]。方差信息準則權衡了貝葉斯模型的擬合優度和復雜度，計算公式為：

(12)

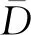
2.4 交通事故預測方法

PET衡量的交通沖突嚴重程度表征了事故發生的風險或交通沖突與交通事故的接近程度。PET值越小，交通沖突與交通事故越接近，當PET≤0時意味著交通事故必然發生。考慮到超閾值極值模型僅適用于大于某一閾值的極值事件，對PET取負變換為NPET(NegatedPET)，此時NPET≥0(即PET≤0)即意味著會發生交通事故。根據上述方法標定得到基于NPET的GPD分布，進而可推導出交通事故的發生概率，即：

R=Pr(NPET≥0)=1-Pr(NPET<0)=

(13)

式中，R為對應沖突觀測時段t的交通事故發生概率。假設沖突觀測時段能夠代表更長時段T的交通運行狀況，那么該時段內的交通事故數NT為：

(14)

3 建模結果分析

利用高速公路合流區PET數據進行貝葉斯層級沖突極值模型構建，其中，考慮的沖突極值非穩態特性影響因素包括加速車道長度(LEN，m)、合流車輛類型(MVT，1，2，3分別代表小、中、大型車)、主線車輛類型(TVT，1，2，3分別代表小、中、大型車)、加速車道小時平均交通量(MVV，veh/h)、主線小時平均交通量(TVV，veh/h)。模型估計時，分位數回歸通過R軟件包quantreg實現，貝葉斯估計通過WinBUGS軟件實現。

3.1 閾值選取結果分析

為保證閾值足夠大從而使超閾值樣本服從GPD分布，本研究首先分別選取了80%,85%和90%這3個分位數，并將LEN，MVT，TVT，MVV，TVV這5個協變量代入分位數回歸模型中進行參數估計，結果表明：3個分位數模型中的顯著變量均為LEN，MVT，TVT，MVV，對應的參數估計結果見表2。

針對每一個分位數進行了GPD分布的參數估計，結果表明：在85%和90%分位數上滿足閾值穩定性要求，即估計得到的修正后的尺度參數和形狀參數基本不變，但在90%分位數上對應的估計值方差較大。考慮到模型估計方差和偏差的平衡，本研究選取85%分位數對應的值為最終閾值，即u=-0.518-2.815×LEN+0.148×MVT-0.150×TVT-0.003×MVV。

3.2 模型標定結果分析

通過向后逐步回歸法構建貝葉斯層級沖突極值模型，即首先將5個變量均通過關聯函數與GPD的尺度參數連接，對應的模型稱為非穩態全模型；進而逐步減少變量的數量直至變量數量為0，此時對應的模型為穩態模型；期間構建的僅包括顯著變量(p<0.05)的模型稱為非穩態顯著模型。

采用Winbugs14軟件對上述模型進行標定時，構造2條包含100 000次迭代的MCMC鏈進行貝葉斯推理。通過檢查2條鏈的迭代歷史圖可確定MCMC算法是否達到收斂；此外，也可以通過BGR(Brooks-Gelman-Rubin)值進行收斂判斷，一般認為BGR值小于1.2時為收斂[22]。將前50 000次迭代視為燃燒樣本，不參與模型參數的估計，利用后50 000 次迭代值進行模型參數估計。穩態模型、非穩態顯著模型、非穩態全模型的估計結果見表3。3個模型均達到收斂，其中非穩態顯著模型中僅有MVT，MVV為顯著變量，對應的迭代歷史和BGR值如圖2和圖3所示。

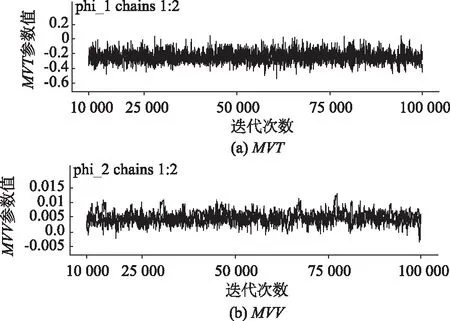
圖2 非穩態顯著模型迭代歷史圖

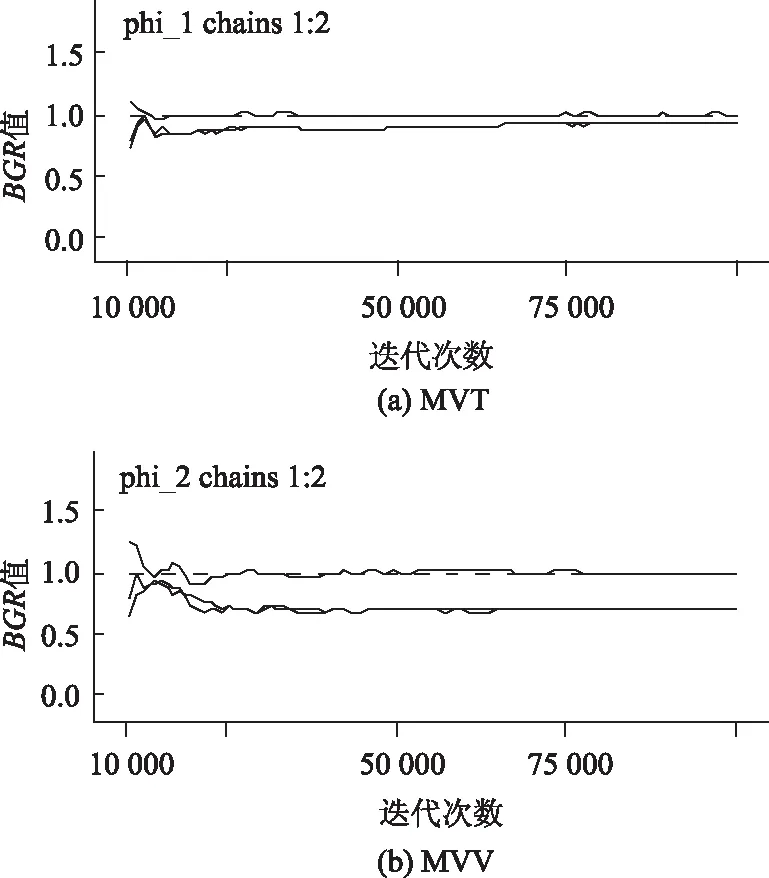
圖3 非穩態顯著模型BGR圖

由表3可知，穩態模型、非穩態顯著模型和非穩態全模型的DIC值分別為6 567.1，6 549.3和6 557.3。相較于穩態模型，非穩態模型的DIC值明顯更小，這說明考慮協變量對沖突極值的影響明顯提高了貝葉斯層級極值模型的擬合優度。此外，兩個非穩態模型中，僅包含顯著變量的非穩態顯著模型的DIC值更小，并且其與非穩態全模型的DIC值之差為8.0。因此，非穩態顯著模型為最優模型。

表3 貝葉斯層級極值模型估計結果

3.3 事故預測結果分析

3.3.1 事故預測精度分析

根據標定的最優模型并結合式(13)、式(14)，計算得到各合流區的預測年均事故數。式(14)中，T=365 d×12 h/d=4 380 h，t=8 h(綏中、高升、五龍背和通遠堡合流區)或7 h(葫蘆島、興城和本溪合流區)。預測事故數與觀測事故數之間的關系如圖4所示。

由圖4可以看出，預測事故數與觀測事故數間具有明顯的正相關關系(計算得出相關性系數ρ=0.820 1，顯著性水平sig=0.023 9)，線性擬合優度值R2=0.670 4。為進一步量化事故預測精度，計算了預測事故數與觀測事故數間的平均誤差(Mean Error,ME)和平均絕對誤差(Mean Absolute Error,MAE)，計算公式為：

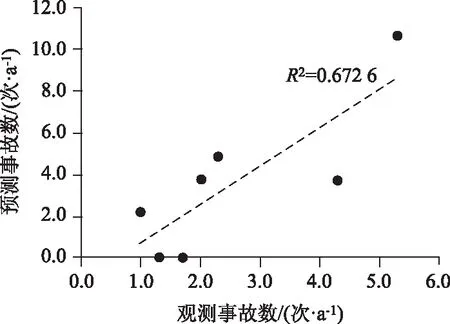
圖4 觀測事故數與預測事故數關系

(15)

(16)

式中，Pi為第i個合流區的預測事故數;Oi為第i合流區的觀測事故數。計算結果見表4，模型預測事故數與觀測事故數之間的平均誤差和平均絕對誤差均較小，分別為1.0次/a和2.1次/a，這說明基于貝葉斯層級沖突極值統計的事故預測方法具有較高的預測精度。此外，平均誤差為正，表明模型在總體上高估了事故發生次數。

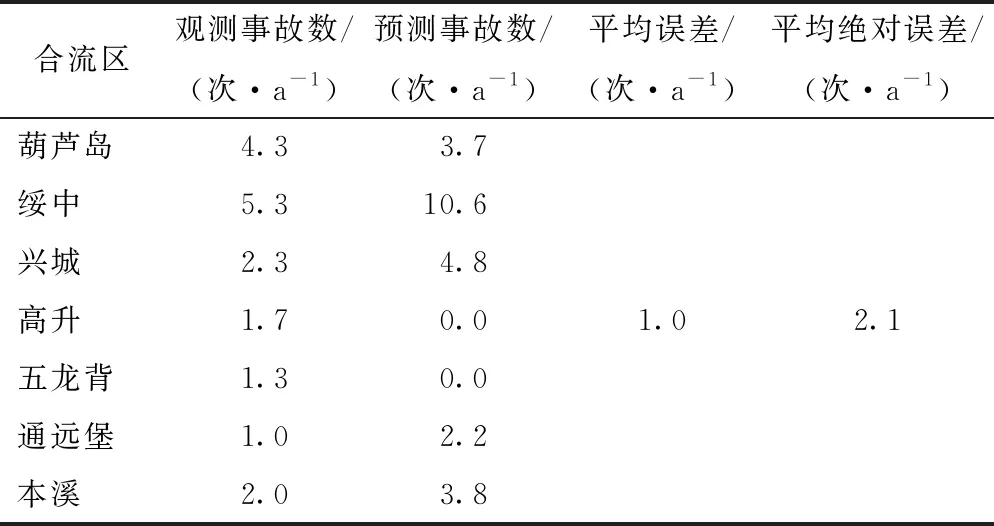
表4 事故預測精度

3.3.2 事故影響因素分析

建模發現，加速車道長度(LEN)、合流車輛類型(MVT)、主線車輛類型(TVT)、加速車道小時平均交通量(MVV)為顯著變量，但這些變量并不直接影響交通事故的風險，而是影響GPD分布的閾值和尺度參數。閾值和尺度參數決定了大部分極值事件的集中度，不同閾值和尺度參數對應的GPD分布示意如圖5所示。當尺度參數和形狀參數保持不變時，閾值越小，GPD分布整體上越偏離事故風險區域(即越安全)；但閾值和形狀參數不變時，尺度參數越大，GPD分布跨度越大，分布曲線的右尾部越可能進入事故風險區域(即越危險)。

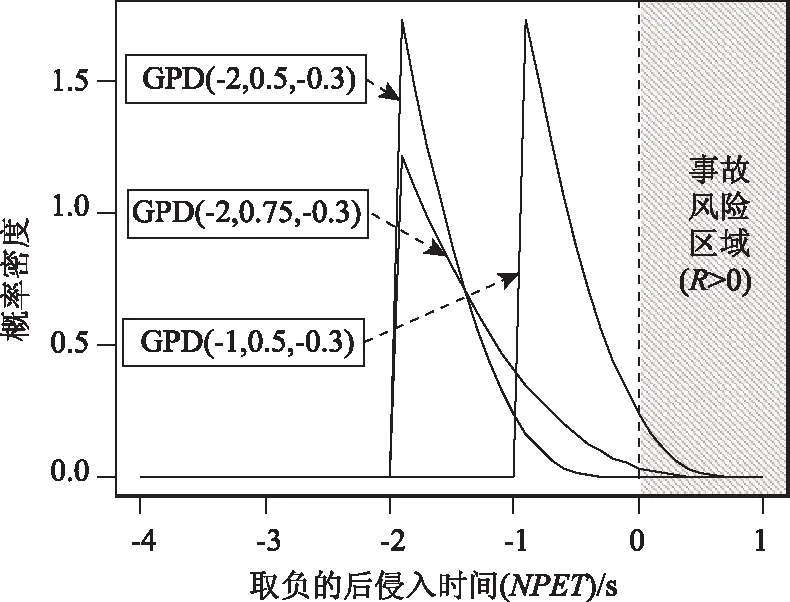
圖5 不同閾值和尺度參數對應的GPD分布示意

上述4個顯著變量中，LEN和TVT僅對閾值有顯著影響，其系數均為負值(分別為-2.185和-0.150)。為了量化分析其對合流安全性的影響，假設其他變量均取其均值，計算得到某一變量值逐漸增大時的事故發生概率，如圖6(a)和圖6(b)所示。由圖可知，LEN和TVT值越大，閾值越小，對應的合流區越安全。即加速車道長度較長時，發生交通事故的風險更低，因為加速車道較長時，合流車輛駕駛員有更為充足的時間完成加速和可接受間隙選擇，因而降低了合流事故風險，但當加速車道長度增加至一定值時，其繼續增加的安全邊際效益則會降低，這也說明加速車道長度并不是越長越好。此外，當主線上有大型車時，合流車輛駕駛員往往更加謹慎，因而合流事故風險會降低。

圖6 變量對合流事故風險的影響

變量MVT和MVV對閾值和尺度參數均有顯著影響，且MVT值越大，閾值越大,尺度參數值越小；MVV值越大，閾值越小,尺度參數值越大。為了綜合分析這些變量對合流安全性的影響，同樣假設其他變量均取其均值，計算得到某一變量值逐漸增大時的事故發生概率。對MVT而言，保持LEN，MVV，TVT不變時，不同合流車型對應的事故發生概率變化如圖6(c)所示，隨著車型的增大交通事故發生概率逐漸降低。由于大型車的尺寸和性能與小型車差異較大，一般認為大型車比例增高會導致交通事故數增加，這與本研究發現存在相悖之處。潛在原因是本研究使用的沖突樣本中車輛類型分布不均衡，合流車輛主要是小型車。對MVV而言，保持LEN，MVT，TVT不變時，合流車流量增加時對應的事故發生概率變化如圖6(d)所示，隨著合流車流量增加，事故發生概率增大。

4 結論

(1)提出了貝葉斯層級沖突極值建模方法，一方面融合了不同地點的沖突極值進行聯合建模，解決了沖突極值的稀少性問題；另一方面引入了協變量和隨機誤差項，解決了沖突極值的非穩態性和異質性問題，顯著提升了模型擬合優度。該方法可實現基于短期觀測沖突數據的交通事故預測，且相較于傳統的基于沖突極值統計的交通事故預測方法更為可靠。

(2)采用貝葉斯層級沖突極值建模方法構建了高速公路合流區交通事故預測模型，結果表明該模型具有較高的預測精度，模型預測事故數和觀測事故數的平均誤差僅為1.0次/a，平均絕對誤差為2.1次/a。

(3)加速車道長度、合流車輛類型、主線車輛類型、加速車道小時平均交通量對沖突極值有顯著影響，進而影響交通事故發生概率。其中，加速車道越長、主線車輛車型越大，交通事故發生概率越小；合流車輛類型越小、加速車道小時平均交通量越大，交通事故發生概率越大。

(4)本研究主要從模型的角度改進了傳統的沖突極值建模方法，但受沖突數據采集時間較短的限制，個別合流區事故預測結果并不理想，下一步將增加采集時間以提升沖突樣本的代表性，收集合流區線形數據以更全面揭示沖突極值的非穩態性，從而進一步驗證貝葉斯層級沖突極值建模方法的優越性。