由粗到細的多級小波變換水下圖像增強

袁國銘，楊光，王金峰，劉海軍，王薇

（1.防災科技學院 應急管理學院，河北 三河 065201；2.防災科技學院 信息工程學院，河北 三河 065201）

1 引言

水下成像被廣泛用于海洋資源勘探、水下環境監測、海底目標識別等領域，然而受光在水中傳播時散射和衰減效應的影響，水下圖像往往呈現模糊、色彩失真、可視度低等退化現象。水下圖像增強作為水下圖像清晰化處理的重要方法被廣泛用于水下機器視覺任務中［1］。

常用的水下增強方法可分為物理模型增強法，非物理模型增強法和深度學習增強法［2-5］。物理模型的增強法利用已有的先驗信息求解水下成像模型中的清晰圖像，具有高效簡潔的優勢。例如Drews等人［6］提出了水下暗通道先驗，即在清晰水下圖像的局部鄰域內，總有像素在藍或綠通道中具有非常低的灰度值，甚至趨于零。Asadi等人［7］將顏色校正與暗通道先驗相結合，進一步提出了優化的暗通道先驗增強算法。雖然知識先驗有助于物理模型估計清晰的水下圖像，但不能描述復雜的水下環境，泛化能力較差。

非物理模型的增強方法旨在修改水下圖像的像素值，以達到視覺滿意的增強效果。Li等人［8］提出了融合白平衡與直方圖拉伸的方法（Hybrid Framework for Underwater Image Enhancement，HUIE），來實現水下圖像的顏色補償。Song等人［9］提出的水下圖像增強方法（Enhancement Registration Homogenization，ERH），通過順序執行增強、配準和均勻化的方式來獲取高質量的水下圖像。為進一步增強細節，Hu等人［10］提 出 了小波變換 增 強 算 法（Enhancement based on Wavelet Transform，EWT），該法將水下圖像分為高頻和低頻部分，對低頻部分實施直方圖均衡化操作以校正顏色，對高頻部分實施對數計算以增強細節。最后實施反小波變換，得到增強的水下圖像。然而，上述算法僅能針對某一種或幾種水域圖像進行增強，應用范圍有限。

近年來，基于神經網絡的水下圖像增強方法備受關注，它通過學習水下圖像與清晰圖像之間的映射關系實施增強，具有較好的泛化能力。例如，Anwar等人［11］提出了水下增強神經網絡（Underwater Enhancement CNN，UWCNN）方法，它利用10種Jerlov水類型的圖像分別訓練UWCNN模型，能有效處理不同水域圖像的顏色差異。Wang等人［12］提出了水下生成對抗網絡（Underwater Generative Adversarial Network，UWGAN），利用生成對抗網絡復原真實的水下圖像，具有較好的魯棒性。Islam等人［13］提出全卷積條件生成對抗網絡（Full Convolutional Conditional GAN based Network，FGAN），并用多模態目標函數來訓練網絡模型，獲得逼近真實場景顏色的視覺效果。近年來，更多學者將傳統增強算法和數學理論融入神經網絡的設計中，取得了較好的圖像增強效果。如He等人［14］，將常微分方程（Ordinary Differential Equation，ODE）的一階歐拉求解策略映射為殘差模塊，提出了ODE啟發的圖像增強模型，該模型因融入了歐拉算法的穩定性和收斂性，具有好的網絡性能。Ma等人［15］將小波變換后的高頻和低頻信息作為增強網絡的輸入，并利用小波雙流網絡（Wavelet-based Dual-stream Network，WDN）的高低頻分支分別處理高低頻的信息，然而雙流分支的設計未考慮頻率域信息屬性，顏色及細節的增強效果有待提高。Sun等 人［16］提 出 了 多 級 小 波 卷 積 網 絡（Multi-level Wavelet CNN，MWN），它利用多級小波變換和反變換來實現水下圖像編碼和解碼，融入的邊緣增強信息，能有效實現細節增強。Zamir等人［17］將傳統方法中由粗到細的復原策略引入到圖像復原框架，從而將復原工作分解為更小，更容易的子任務，以便高效實施圖像去雨、去噪和去模糊。上述算法或關注顏色校正，或關注邊緣增強，或關注結果細化，不能同時實施顏色校正，細節增強及結果細化，獲得滿意的結果。

本文提出了由粗到細的多級小波變換水下圖像增強網絡，它包含多級小波變換的圖像增強子網絡和二階龍格庫塔模塊的細化子網絡，用以校正顏色，增強細節和細化結果。具體來說，首先，利用多級小波變換將水下圖像分解為低頻圖像和一系列高頻圖像。隨后，在多級小波變換的圖像增強子網絡中，設計融入實例歸一化和位置歸一化的低頻分支，以消除低頻圖像中不同水域類型帶來的顏色差異。同時，聯合低頻和高頻信息設計基于掩模增強的高頻分支，用以增強高頻圖像中的邊緣和細節；實施反小波變換，獲得初步增強的水下圖像。設計ODE啟發的二階龍格庫塔模塊，并用此構建細化網絡，對初步增強的結果進一步細化。實驗表明，本算法較已有的水下圖像增強算法，具有更好的增強效果，PSNR值的提升幅度達9%。滿足水下視覺任務的顏色校正，細節增強，清晰化要求。

2 由粗到細的多級小波變換水下圖像增強

本文提出了由粗到細的多級小波變換水下圖像增強網絡，它包含由粗到細的兩個階段，分別為：多級小波變換的圖像增強子網絡和二階龍格庫塔模塊構建的細化子網絡。網絡框架如圖1所示。

對于輸入的水下圖像I∈Rh×w×3，首先利用多級Haar小波變換將I分為多個頻率帶，以便根據不同頻率帶包含的信息，實施相應的圖像增強操作。具體來說，Haar它包含低通濾波器L和高通濾波器H：

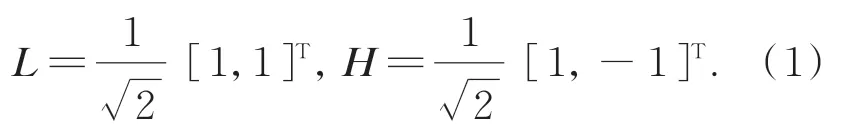
對I實施低通濾波LLT，得到低頻圖像IL∈Rh/2×w/2，對 圖 像I實 施LHT，HLT，HHT濾波，則得到垂直，水平，對角線方向的高頻圖像IH=[ILH，IHL，IHH]，IH∈Rh/2×w/2。對 低 頻 圖 像重復實施小波變換，可實現二級，三級以至多級小波變換。假設n為小波變換的級數，實施多級Haar小波變換后，得到低頻圖像InL，尺寸為h2n×w2n，高 頻 圖 像InH，In-1H，In-2H，尺 寸 為h2n-1×w2n-1，默認n=3。

2.1 多級小波變換的圖像增強子網絡

對于包含顏色信息的低頻圖像InL，旨在消除不同種水域類型產生的顏色差異，這里將顏色校正問題看作隱式的類型轉化問題，并設計基于實例歸一化和位置歸一化處理的低頻分支。對于包含細節的高頻圖像InH，In-1H，In-2H，旨在如實地增強細節。為減少計算成本，聯合第n級小波分解獲取的低頻和高頻信息計算掩模，并設計基于掩模增強的高頻分支。在對高低頻圖像實施處理后，利用逆小波變換，得到初步增強的結果。

2.1.1 低頻分支設計

本文將低頻圖像的顏色校正問題看作隱式的風格轉換問題，并將風格轉換中常用的實例歸一化（Instance Normalization，IN）和位置歸一化（Position Normalization，PN）用于低頻分支的設計中［18］。這里，IN具有空間域中內容對比度的不變性，而PN能在通道空間中捕獲圖像的類型和形狀信息。將IN和PN引入低頻分支設計中，能在空間和通道域里自適應地調節輸入特征的均值和方差，消除顏色差異。PN和IN均可由式（2）解釋：

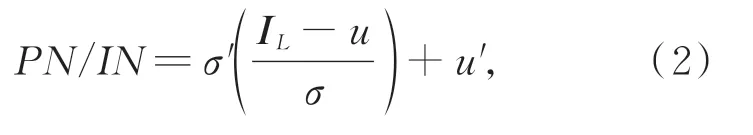
式中：u和σ為特征的均值和標準方差。u'和σ'為從輸入特征中學習的仿射參數。

低頻分支的結構如圖1所示，首先利用兩個卷積對第n級小波變換（n=3）的低頻圖像InL逐步實施通道擴展，得到特征FL。隨后對FL實施PN操作，即提取所有通道數下的特征均值uc和方差σc：

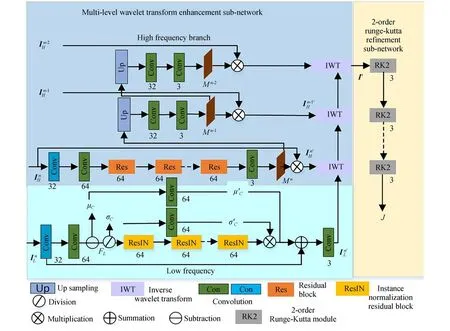
圖1 由粗到細的多級小波變換水下增強網絡框架Fig.1 Architecture of coarse-to-fine network for underwater image enhancement based on multi-level wavelet transform

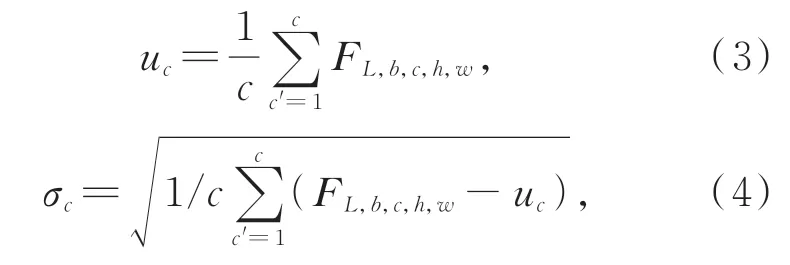
式中：b，c，h，w分別為特征FL的批大小，通道數，高和寬。c'為通道索引。歸一化的FL輸入到文獻［18］中所提的5個ResIN模塊中，該模塊包括1個 卷 積 層，1個IN層，1個ReLU激 活 函 數 以 及殘差連接。其中，IN的特征均值uhw和方差σhw計算公式如式（5）和式（6）：

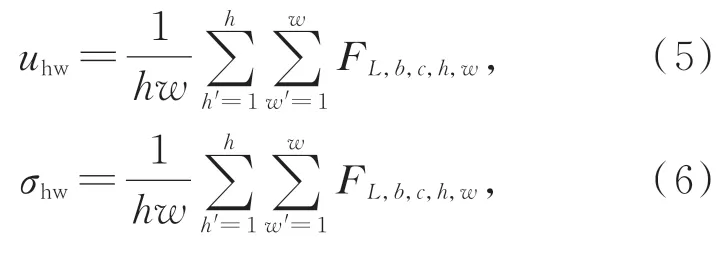
式中：h'和w'為高和寬的索引，h，w為特征的高和 寬。FL，FL，b，c，h，w同 公 式（3）和（4）中 的 變 量。IN操作摒棄了提取的空間統計信息如uhw，σhw，而所學的仿射參數u'hw和σ'hw能有效消除不同水域類型導致的顏色差異；最后ResIN輸出的信息進一步由PN所學的仿射參數u'c，σ'c調整（見圖1），并通過一個卷積將通道數減少至與InL相同的通道數，得到InL'。

2.1.2 高頻分支設計

本文將高頻分支的細節增強處理，看作為低頻分支實施風格轉換時的對應操作。為了能如實地增強水下圖像，細節的增強需與低頻分支實現InL至InL'風格轉換操作保持一致，因此本文擬利用InL，InL'信息來實現InH的增強。然而，具體如何實施InH的增強操作，仍是有待解決的問題。圖2顯示了初始的水下圖像（圖2（a））及增強的水下圖像（圖2（c））在分別實施一級小波變換后獲取的2張高頻圖2（b）及圖2（d）。他們在細節分布上基本一致，僅在亮度上存在差異，如圖2（d）中箭頭所示的細節點，相比圖2（b）中對應位置處的細節點亮度更亮。因此，本文擬聯合InL，InL'及InH生成細節增強掩模，并將掩模與高頻圖像InH相乘，以便自適應地調節全局亮度信息。值得一提的是，掩模的生成，不但利用了低頻分支風格轉換的顏色信息InL，InL'來調節全局亮度，確保細節增強與低頻分支實施風格轉換操作保持一致，還利用了包含細節的高頻圖像InH信息，故增強操作能同時兼顧細節及亮度。細化高頻圖像的掩模Mn的計算表達式如式（7）所示：

圖2 初始圖像及增強圖像的比對Fig.2 Comparison between initial images and enhanced images

式中：↑為雙線性插值上采樣操作，它將尺寸為h2n×w2n的InL和InL'上采樣至h2n-1×w2n-1，以便與InH尺度匹配；[?]為串聯操作；f1為復合操作的函數，該復合操作包含2個卷積層和5個去除IN操作 的Res模塊［18］。InH為高頻圖像。最后 的卷積層將輸出通道為3的掩模Mn。利用Mn細化InH，以得到細化高頻圖像InH'，具體表達式如式（8）所示：

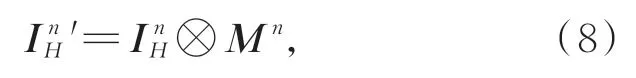
式中，?為點乘操作。

實際上各級小波變換獲得的高頻圖像包含相同的細節和紋理信息，僅在微小細節上存在差異。如圖3所示，初始水下圖像（圖3（a））的一、二、三級小波變換高頻圖像IHH（見圖3（b）～3（d）），僅在沙粒細節上存在差異，即隨著小波分解的級數越多，沙粒細節越少。為提高計算效率，本方法在第n級小波變換的高頻分支上計算掩膜Mn，并上 采 樣 及細化后，對n-2，n-1級小波變換的高頻圖像進行全局的細節增強。

圖3 各級小波變換獲得的高頻圖像Fig.3 High frequency image obtained by wavelet transform at different levels

具體來說，可對Mn實施雙線性插值上采樣，得到細化In-1H，In-2H的掩膜Mn-1，Mn-2。表達式為：

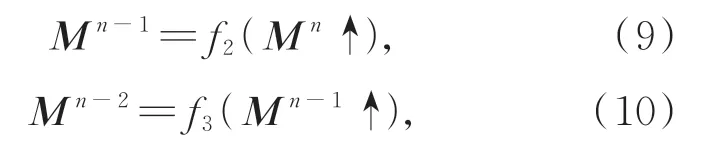
式中：↑為雙線性插值上采樣，它們分別將n級小波變換時獲取的掩模Mn和n-1級小波變換時獲取的掩模Mn-1尺度上采樣至In-1H，In-2H的相同大小；f2和f3為復合操作的函數，它們均包含2個3×3的卷積層，用于細化上采樣掩膜。依據公式（8），即 可 得到 細 化 的In-1H'，In-2H'。對InL'，InH'，In-1H'，In-2H'實 施 逆 小 波 變 換，獲 得 增 強圖像I'。

2.2 二階龍格庫塔模塊構建的細化子網絡

堆疊的殘差模塊被廣泛地用于圖像復原的細化中［14］。實際上，殘差模塊可看成是ODE前向歐拉求解策略的映射，堆疊的殘差模塊可視為離散的一階歐拉逼近ODE求解過程。為獲取更優的增強結果，本文設計了基于二階龍格庫塔（Runge-Kutta）模塊的細化子網絡。具體來說，一階ODE問題可由一階微分方程及初始條件實施求解：

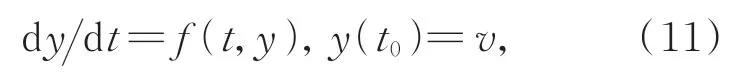
式中：f(t，y)為變量t，y的函數，dydt為函數y對自變量t的一階導數，y(t)∈Rd為自變量t的函數y，且t≥t0，y(t0)=v為初始條件。

依據一階的歐拉求解策略，dydt可表示為離 散 形 式(y(tn+1)-y(tn))(tn+1-tn)，n=0，1，…，n，則公式（11）可用式（12）來表示：

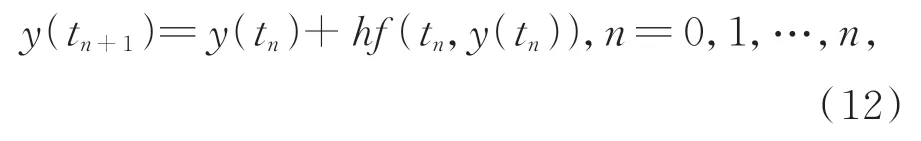
式中，h=tn+1-tn。研究表明殘差模塊也有相似結構：

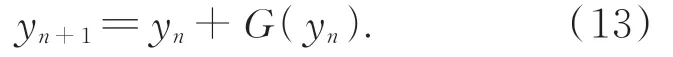
由此可見，若將式（12）中的y(tn+1)和y(tn)分 別 看 成yn+1和yn，而G(yn)=hf(tn，y(tn))，則殘差模塊即為一階歐拉方法的映射模塊，在細化網絡中堆疊的殘差模塊，則可視為離散的歐拉逼近求解過程。考慮到二階龍格庫塔方法相比于一階歐拉方法，具有更小的局部截斷誤差及穩定性［19］，能更精確地求解ODE，本文設計基于二階龍格庫塔的RK2模塊，并堆疊5個RK2模塊構建細化網絡，由此將二階龍格庫塔方法的優越性引入到網絡性能中，獲得更佳的細化效果。

二階龍格庫塔模塊設計如下。

由數值ODE理論可知，二階龍格庫塔方法利用梯形公式來實施求解：

式 中：tn+1可 由tn+1=h+tn計 算 得 到；yˉn+1可 用它的一階逼近，即公式（13）的yn+1來替代。依據公式（13）中G(yn)=hf(tn，y(tn))的映射關系，可獲得表達式（15）～式（17），由此得到RK2模塊結構圖如圖4所示。

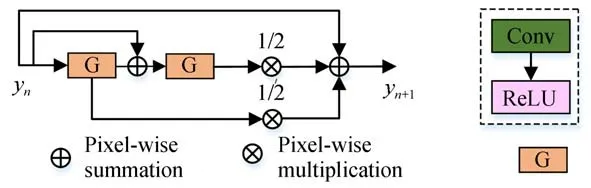
圖4 RK2模塊結構Fig.4 Architecture of RK2 block

2.3 損失函數

在模型的訓練過程中，我們通過最小化L2函數來減少圖1中I'，J與真實結果G之間的差異。假設I'i，Ji和Gi，i=1，2，…，m為一組小波變換增強圖像，細化網絡增強圖像和真實水下圖像，則對應的損失函數L可表示如式（18）：

式中：α為平衡系數，默認取1。

3 實驗結果與分析

3.1 數據集

為確保由粗到細的多級小波變換水下圖像增強網絡具有較好的泛化能力，本文擬選用文獻［11］提供的數據集來進行訓練和測試。該數據集依據水下成像物理模型對1 449張NYU-V2室內圖像進行水下成像合成，即每張圖像合成I，IA，IB，II，III，1，3，5，7，9共10種水域類型的圖像，共計合成圖像14 490張，其中13 041張圖像為訓練集，1 449張圖像為測試集1（文中標記為Test1）。另一方面，選用文獻［20］提供的890張真實水下圖像及其高質量參考圖像為測試集2（文中標記為Test2），這里高質量參考圖像是由25位從事圖像處理領域的志愿者和25位從事其他領域的志愿者，共同從12種水下圖像增強算法的結果中逐一挑選出來。為客觀評價各算法增強結果的質量，采用全參考的圖像質量評價指標：信噪比/相似度PSNR/SSIM、局部批次對比度PCQI、邊緣強度EI，以及無參考圖像質量評價指標：UIQM，UCIQE和信息熵Entropy。其中，PSNR/SSIM，PCQI及EI在合成及真實圖像測試集的真實（參考）圖像幫助下，測量增強圖像的質量，對比度變化及邊緣強度，其值越高則增強算法的性能越好。另一方面，非參考的評估指標UIQM是基于人眼系統激勵的無參考水下圖像評價指標，它利用色調、對比度和清晰度的加權組合來綜合評價水下圖像的質量，避免了單一指標評價的局限性，其值越高，水下圖像的質量越好。與UIQM類似，UCIQE是用CIELab空間 的色度、飽和度、對比度的線性組合來評價彩色水下圖像的質量，其值越高，圖像質量越好。Entropy能反映圖像中信息量，值越大包含的信息越多［21］。

3.2 算法實施細節

水下圖像增強網絡在NVIDIA RTX 2080 Ti GPU的PC機 上，通 過 搭 建Pytorch深 度 學 習框架實現。網絡框架中小波變換級數n=3，共包含12個 卷 積 層，5個ResIN模 塊，5個Res模 塊，2個 上 采樣操作及5個RK2模 塊，其中ResIN模塊參數設置為文獻［18］中ResIN模塊的默認設置，因Res模塊為去除IN操作的ResIN模塊，故參數同［18］。上采樣采用雙線性插值法，模型中12個卷積層及RK2中涉及的卷積層共有兩種不同的參數設置：圖1（彩圖見期刊電子版）中藍色卷積層，核大小為1×1，步長為1，填充為0。其余綠色卷積層，核大小為3×3，步長為1，填充為1。各層/模塊輸出通道數標于圖1各層/模塊下方。

優化函數Adam算法的學習率為0.000 1，β1=0.9，β2=0.999。訓練及測試時的輸入圖像大小均為512×512，批大小為4，訓練200 epochs。

3.3 網絡結構及參數分析

水下圖像增強網絡包含多級小波變換的圖像增強子網絡和二階龍格庫塔模塊構建的細化子網絡。其中，多級小波變換圖像增強子網絡的低頻分支和高頻分支分別包含5個ResIN模塊和5個Res模塊，細化子網絡中則包含5個RK2模塊，模型在Test1上結果為24.51/0.886 7。為了驗證構建模塊數的有效性，本節首先分別測試不同組件包含的不同模塊數時網絡的性能，即高頻分支包含Res模塊數為3，4，6時，對應變異模型Res_3，Res_4，Res_6的性能；低頻分支包含ResIN模塊數為3，4，6時，對應變異模型ResIN_3，ResIN_4，ResIN_6的性能；細化子網絡 包 含RK2模 塊 數 為3，4，6時，應 變 異 模 型RK2_3，RK2_4，RK2_6的 性 能。結 果 如 表1所示，當網絡結構不變，增加任一模塊（ResIN模塊，Res模塊或RK2模塊）數量時，網絡性能均有不同程度的提升，但當ResIN模塊增至6時，性能微微下降，而增加Res和RK2至6時，其量化結果雖高于所提模型結果24.51/0.886 7，但差距微小。為平衡網絡參數和性能，所提模型設置的模塊數最優：ResIN模塊，Res模塊及RK2模塊的數量均為5。在此基礎上，討論多級小波變換的圖像增強子網絡及細化子網絡結構設計的優越性。

表1 測試集1上不同構建模塊數的模型量化結果對比Tab.1 Comparison of quantitative results by variant models with different number of building modules on Test 1.

為驗證多級小波變換的圖像增強子網絡有效性，本文分別測試了小波變換級數n=1，2，3，4，5，6的情況，相應的變異模型在合成圖像測試集上的量化結果如表2所示，從中可見，隨著n增加，網絡性能逐步提高，當n=3時，模型能獲得最高的PSNR和SSIM，此后隨著n增加，網絡性能略微下降，但仍具有較好的魯棒性，如n=4較n=3而 言，PSNR值 僅 從24.51下 降 到24.48，為平衡計算成本和精度，本文選擇n=3為小波分解級數。

為驗證圖像增強子網絡的有效性，設計了兩個變異模型：Net-w/o-lb和Net-w/o-hb。Net-w/o-lb在保持所提網絡結構不變的基礎上，將n級小波變換（n=3），低頻分支中的PN和ResIN移除，僅保留圖1低頻分支中兩個卷積操作，以驗證低頻分支顏色校正的有效性。Net-w/o-hb則在原網絡模型的基礎上，移除掩模計算及相乘操作，直接將各級小波變換獲得的高頻圖像，輸入到兩個卷積層中，得到處理后的高頻信息，以驗證高頻分支實施掩模增強的有效性。如表2所示，Net-w/o-lb和Net-w/o-hb在合成圖像測試集上的量化結果低于所提網絡模型（n=3）的結果，證明高頻分支及低頻分支能有效提升水下圖像增強的性能。

表2 測試集1上不同變異模型的量化結果對比Tab.2 Comparison of quantitative results by different variant models on Test1.

為驗證ODE啟發的細化子網絡及其構建模塊RK2的有效性，設計了Net-w/o-R和Net-Res變異模型。Net-w/o-R將原始網絡中的細化網絡移除，即將基于多級小波變換的水下圖像增強子網絡輸出結果I'作為最后的增強結果，以驗證細化網絡的有效性。Net-Residual則將細化網絡中RK2模塊替換為殘差模塊，以驗證RK2模塊的優越性。兩個模型在合成圖像測試集上對應的測試結果如表2所示，較所提網絡而言，變異模型的性能明顯下降，從而證明基于RK2模塊的細化網絡有效性和必要性。

為驗證訓練參數epoch設置的合理性，視覺化訓練過程中loss函數值曲線及每個epoch時訓練模型在Test1上的PSNR值。如圖5所示，隨著epoch數的增加，loss值不斷降低，且在約180 epochs時模型收斂。圖6同理，模型訓練過程中測試集的PSNR值也在約180 epochs時趨于穩定。因此，將模型訓練次數設置為200 epochs能確保模型收斂，獲得最優性能的網絡模型。

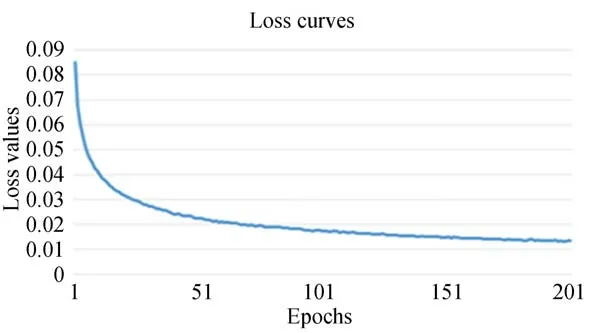
圖5 訓練過程中loss函數值Fig.5 Loss curves during training.

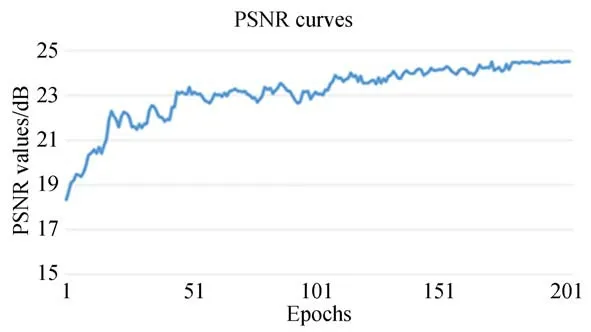
圖6 訓練過程中測試集的平均PSNR值Fig.6 Average PSNR of testing data during training.

3.4 合成水下圖像增強結果對比

為評測所提網絡模型的增強效果，本節將在合成水下圖像測試集Test1上，比較本文算法與8個已有的水下圖像增強算法的性能，包括傳統的HUIE算法［8］，ERH算 法［9］，EWT算法［10］以 及基 于CNN的UWCNN算 法［11］，UWGAN算法［12］，FGAN算 法［13］，WDN算 法［15］，MWN算法［16］。其中，UWCNN算法分別采用10種不同水類型的圖像訓練，得到10個水下增強模型，本文選取水域類型為1的水下圖像訓練模型進行測試。表3為各算法的量化結果，從中可見本文算法具有最高的PSNR與SSIM值，表明本文算法的優化結果最接近真實結果。此外，最高的UCIQE，UIQM和PCQI值，也說明本文算法能更好地平衡水下圖像的色調、對比度、清晰度及飽和度。在PCQI，Entropy和EI指標上，本文算法的量化結果也高于比較算法，證明本文算法有效地增強場景細節，而不是噪聲。

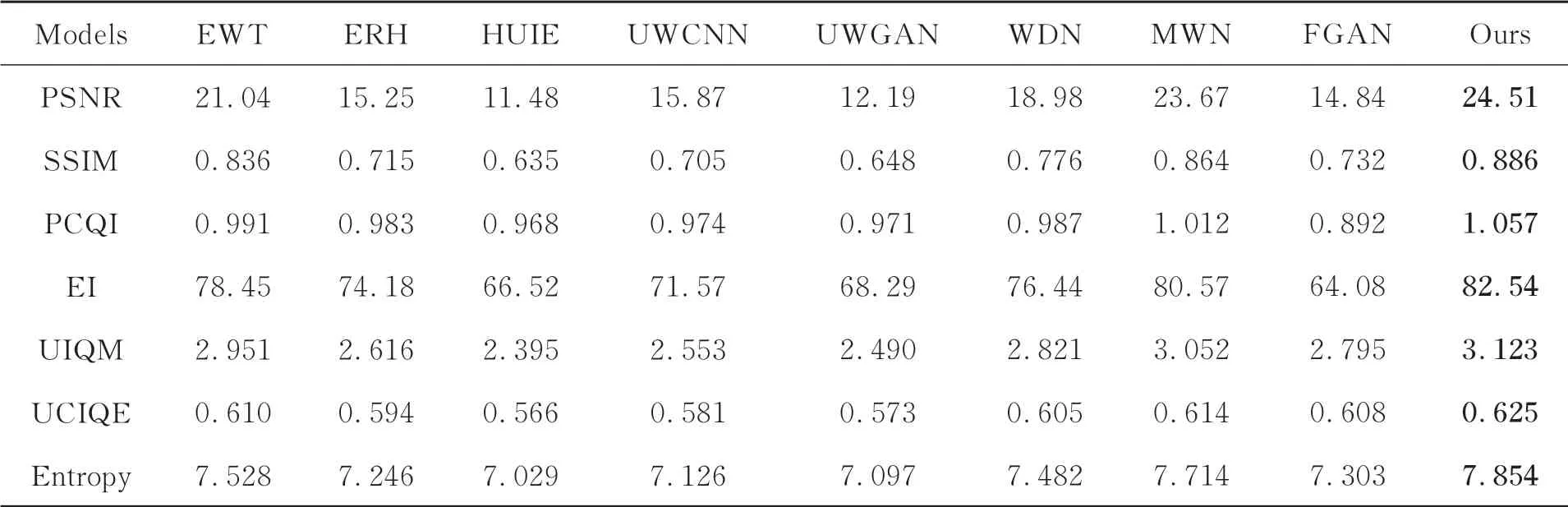
表3 不同算法在測試集1上的量化結果對比Tab.3 Quantitative comparison of enhanced results by different algorithms on Test1.

為進一步對比視覺增強效果，從Test1中選取了3張水下圖像進行展示，包括合成的渾濁水域圖像，低照明圖像，藍綠色水域圖像（見圖7（a））。各算法的視覺增強結果如圖8（a）～8（i）所示。結果表明，EWT算法能拉伸圖像的對比度，提高低照明圖像的亮度，并在一定程度上增強水下圖像的細節，但對于藍綠色水域圖像，仍存在顏色失真和細節丟失的問題，如圖8（a）第3行。ERH算法雖有一定的顏色校正能力，但增強結果（見圖8（b））整體偏暗，細節丟失嚴重，與真實結果（見圖8（j））的差異較大。HUIE算法，UWCNN算 法，UWGAN算法和FUnIEGAN算 法 結果存在明顯的色偏現象，如圖8（c）第1行結果偏藍，而圖8（d），8（e），8（h）結果偏黃，且增強結果出現一定程度的模糊。WDN及MWN方法能有效去除色偏，增強細節，但對藍綠水水域圖像的增強效果較差，圖8（f）和8（g）的背景呈現出失真的暗紅色，且細節模糊。相比而言，本文算法的結果圖8（i）在亮度，清晰度及色差平衡力方面明顯優于已有的增強算法，且紋理細節信息也更加突出，接近于圖8（j）的真實結果。圖8下方標出的PSNR/SSIM值進一步證明了本文算法的有效性（彩圖見期刊電子版）。

圖7 測試案例Fig.7 Testing samples

圖8 合成水下圖像增強結果對比Fig.8 Comparison of enhanced results on synthetic underwater images

3.5 真實水下圖像增強結果對比

為驗證所提算法的泛化能力，在包含890張真實圖像的Test2測試集上進行對比實驗。由于Test2提供了真實水下圖像的參考圖，故可量化各算法的增強結果。圖9為不同算法對3幅真實水下圖像（圖7（b））增強的視覺對比圖，包含綠色水域圖像，藍色水域圖像及淺水域圖像，圖9（a）～圖9（h）為對比算法的增強結果，圖9（i）為本文算法結果，圖9（j）為增強參考圖像（彩圖見期刊電子版）。為了更好地觀察細節，圖9的第2，4和6行分別為第1，3和5行的細節放大圖。從圖9可見，EWT因引入了多級小波變換的增強策略，具有較好的視覺增強效果，但在顏色校正上，出現了紅通道過度補償的問題，如圖9（a）第1，2行的手和第5，6行巖石的顏色均偏紅。ERH，UWCNN，UWGAN，WDN和FUnIEGAN算法結果存在色調失真，如圖9（b），9（d），9（e），9（f），9（h）的第3，4行背景偏暗，與真實情況不符。HUIE算法結果出現了部分增強區域，色度不自然的問題，如圖9（c）第4行魚的色度過亮。MWN算法具有較好的增強效果，但對細節豐富的巖石，仍具有邊緣模糊現象，如圖9（g）第4行。本文算法的結果圖9（i）具有最好的清晰度和對比度，其細節甚至比圖9（j）的增強效果更佳，如圖9（h）第2行手部相較圖9（j）更接近真實顏色。圖9下方標出的PSNR/SSIM值進一步證明了本文算法的強泛化能力。

圖9 真實水下圖像增強結果對比Fig.9 Comparison of enhanced results on real underwater images

此外，各算法增強結果的量化指標值如表4所示，本文算法在各指標上仍具有最高值，其中PSNR值較已有算法提高了至少9%，可見客觀評價和主觀評價相符。為了更直接地展示不同算法在不同數據集上的性能，圖10分別為各算法在Test1和Test2上平均PSNR。從中可見，ERH，HUIE，UWGAN，FGAN算法在真實圖像集Test2上具有較合成圖像集Test1上更好的增強效果，而EWT，UWCNN，WDN，MWN及本文算法則在合成圖像集Test1上具有較真實圖像集Test2上更好的增強效果。這是由于，ERH，HUIE，UWGAN，FGAN算法面向真實水下圖像實施增強，旨在獲取逼近真實場景的視覺效果，而本文算法及EWT，UWCNN，WDN，MWN算法利用不同水類型的合成圖像實施訓練，訓練集中未能包含真實場景中所有復雜的降質情況，故出現性能下降。在后續的工作中，將考慮真實圖像的信息分布情況，提高穩定性和泛化能力。

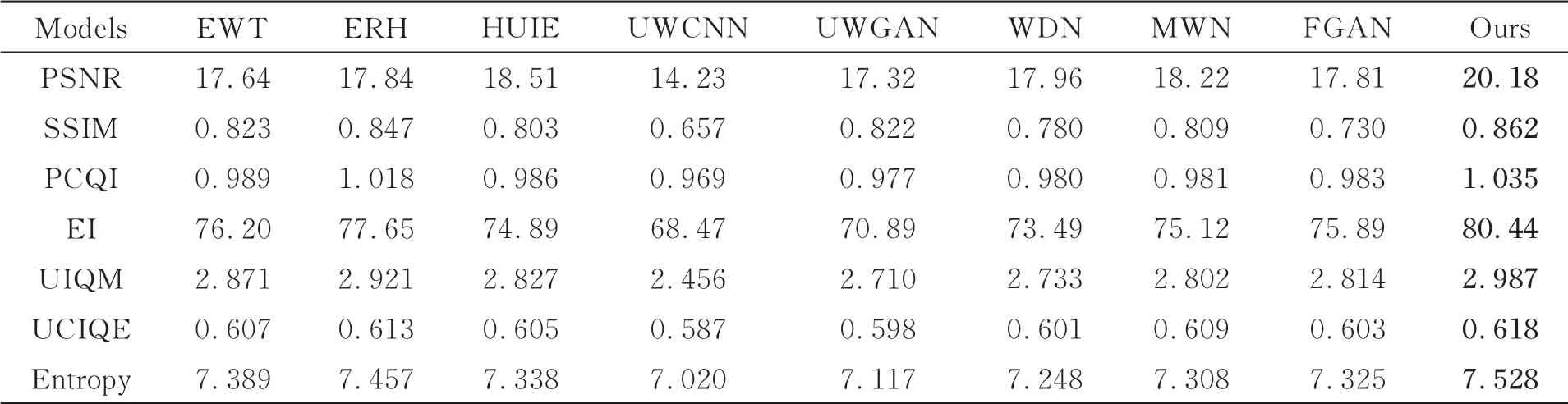
表4 不同算法在測試集2上的量化結果對比Tab.4 Quantitative comparison of enhanced results by different algorithms on Test2.

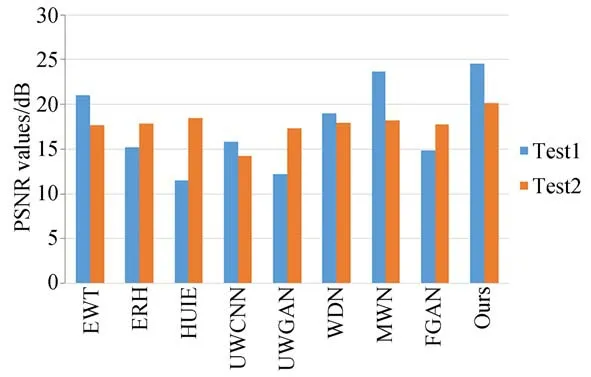
圖10 各算法在Test1和Test2上的PSNR值Fig.10 PSNR of different algorithms on Test1 and Test2.

4 結論

為實現水下圖像的顏色校正和細節增強，本文提出了由粗到細的多級小波變換水下圖像增強網絡，它包含多階小波變換的圖像增強子網絡和二階龍格庫塔模塊構建的細化子網絡。多階小波變換的圖像增強子網絡用于初步估計水下圖像增強的結果，它利用多級小波變換將水下圖像分解為低頻圖像和一系列高頻圖像，并設計相應的低頻分支和高頻分支分別處理低高頻圖像。低頻分支利用類型轉換中常用的實例歸一化和位置歸一化操作實現低頻圖像的顏色校正。高頻分支聯合高低頻信息計算增強高頻圖像的掩模，來實施細節和紋理的增強。隨后，實施反小波變換得到第一階段估計的水下增強圖像。為進一步細化增強結果，設計了ODE啟發的二階龍格庫塔模塊，它具有較殘差模塊更好的穩定性和收斂性，用此構建細化網絡具有更優的細化結果。實驗結果表明，在合成和真實水下圖像集上，本文算法具有較好的視覺和量化增強效果。然而，算法雖利用不同水類型的合成圖像實施訓練，但訓練集中仍未能包含真實場景中所有復雜的降質情況，故算法在真實圖像數據集上的性能較合成圖像數據集上的性能低。在后續工作中，將在模型的設計和訓練中更多地考慮真實圖像的信息分布情況，提高模型的穩定性和泛化能力。