集成電路X射線圖像的多正則化圖像復原

馬鴿，林森，李致富，趙志甲，鄒濤

（廣州大學 機械與電氣工程學院，廣東 廣州 510006）

1 引言

X射線成像是通過發射X射線穿透被檢測元器件，依據待檢測元器件內部產生的射線能量衰減情況及其衰減強度的不同，由平板探測器將衰減數據轉換成數字圖像傳遞給計算機的過程。X射線成像檢測是通過不同材料對X射線的吸收差異，對物體內部結構成像然后進行內部缺陷檢測的技術。因其成像具有分辨率高、無損、非接觸等優點，在集成電路精密制造業、航空航天、特種裝備檢測等領域取得了廣泛關注［1-3］。然而，集成電路的X射線圖像成像過程中存在多個噪聲來源，如電子隨機熱運動產生的熱噪聲、X射線源光子累積產生的噪聲等，因此表現出噪聲強烈的特點。同時，集成電路多層封裝間隔微小，X射線出射距離短，因此呈現出對比度低的特點，給后續識別檢測工作帶來很大困難。因此，研究X射線圖像復原技術具有理論意義和實際應用價值。

文獻［4］將熱噪聲和光子累積噪聲分別建模為加性噪聲和乘性噪聲，得到集成電路X射線成像的混合噪聲退化模型。但是由于工業生產的快速性要求，實際過程中常采用加大電壓的方式實現快速累積成像，大大減少了泊松特性，因此文獻［5］將其建模為高斯加性噪聲退化模型。

圖像復原是從采集的退化圖像獲得原始干凈圖像的逆過程。復原方法包括濾波方法和正則化方法，濾波方法通常具有確定性的濾波函數，如高斯濾波、中值濾波、逆濾波等，但往往受限于噪聲去除和細節保持的平衡問題，而正則化方法因其靈活多變的圖像先驗知識模型和求解算法，被廣泛地應用于工業檢測、機器視覺、醫學診斷等領域［6-9］。

正則化方法將圖像復原問題歸結為由數據保真項和正則化項組成的目標函數模型求解問題。常用的正則化模型可分為基于l1范數的模型和基于全變分的模型兩大類。l1范數刻畫圖像的邊緣細節信息，具有較好的細節保持能力。尤其地，通過小波變換、字典分解等［10-12］可充分利用圖像的稀疏特性來降低數據冗余帶來的采樣數據存儲和硬件設備困難的方法，被廣泛地應用于核磁共振成像、醫學CT圖像重建、圖像稀疏重建等領域［13-14］。

全變分（Total Variation，TV）正則化模型［15］最初于1992年由Rudin，Osher和Fatemi提出，但該模型易產生“階躍”現象，呈現“分片常數”效應。文獻［16］則將保真項等效變換到微分空間，并采用ADMM（Alternating Direction Method of Multipliers）分裂算法進行求解獲得了快速準確的復原效果。

但是，以上方法均對整幅圖像進行統一處理，采用單一的正則化約束條件或者組合的多正則化約束進行求解，容易造成去噪不徹底或過度平滑。文獻［4］對集成電路X射線圖像的加性噪聲和乘性噪聲分別采用TV正則化項和l1正則項進行約束，并采用顯式差分算法和梯度投影（Gradient Projection，GP）算法進行求解獲得了很好的去噪效果。

本文基于圖像邊緣細節、平滑特征和不同正則化項的復原特點，提出集成電路X射線圖像的多正則化圖像復原算法。該方法采用高斯高通濾波和高斯低通濾波分別獲取圖像的邊緣細節結果和平滑濾波結果，充分利用l1正則項在細節保持以及TV正則項在噪聲去除上的優越性，對邊緣細節結果和平滑濾波結果分別采用l1正則化項和TV正則化項約束進行求解，進而獲得完整的集成電路X射線圖像復原結果，解決整幅圖像采用單一正則化項可能造成的細節過度平滑缺失和去噪效果差等問題。

2 基于快速傅里葉變換的圖像濾波方法

集成電路的X射線圖像退化模型可表示為：

其中：f∈RM×N是觀測到的退化圖像，H為觀測陣，x為待求解的干凈圖像，n是符合均值為μ、方差為ξ的高斯分布n～N（μ，ξ）的加性噪聲。

圖像的傅里葉變換是將圖像由空間域變換至頻率域，其中低頻對應集成電路X射線圖像內變化較為緩慢的灰度分量，簡記為平滑特征；高頻對應圖像內變化較快的灰度分量，多表現為邊緣細節部分，因此，本節基于快速傅里葉變換（Fast Fourier Transform，FFT）計算速度快、效率高的特點，分別采用高斯低通濾波和高斯高通濾波獲得低頻對應的平滑濾波結果和高頻對應的邊緣細節結果。

具體步驟如下：

第一步，對觀測圖像f進行快速傅里葉變換得 到 其 頻 譜F(u，v)，其 中u=0，1，…，M-1，v=0，1，…，N-1，F(·)是傅里葉變換；

第二步，對頻譜F(u，v)作能量估計，設定濾波器截止頻率D0。

選定初始截止頻率，獲取高斯低通濾波后的F'(u，v)。逐步增大截止頻率并不斷計算當前截止頻率條件下的F'(u，v)，當滿足條件（2）時，當前截止頻率記為濾波器的截止頻率D0。

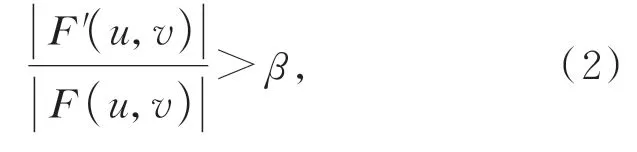
其中：|F(u，v)|表 示 整 個 圖 像 頻 譜 的 能 量，|F'(u，v)|表示高斯低通濾波后頻譜的能量，β∈(0，1)為經驗常數，用于選取濾波器的截止頻率；

第三步，基于高斯低通濾波和高斯高通濾波原理對圖像進行頻域濾波，獲取低頻部分Fsmooth(u，v)和高頻部分Fdetail(u，v)。

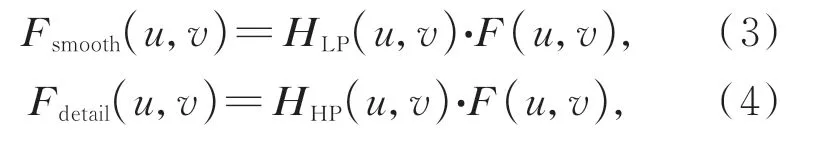
其中：

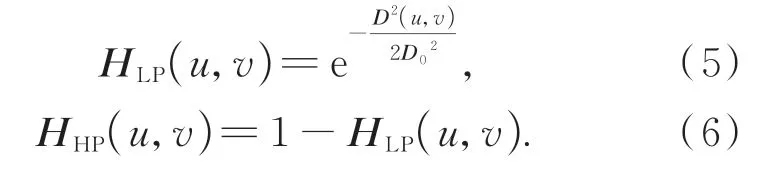
第四步，對低頻和高頻部分進行反傅里葉變換，獲得低頻對應的圖像平滑濾波結果fsmooth和高頻對應的圖像邊緣細節結果fdetail。

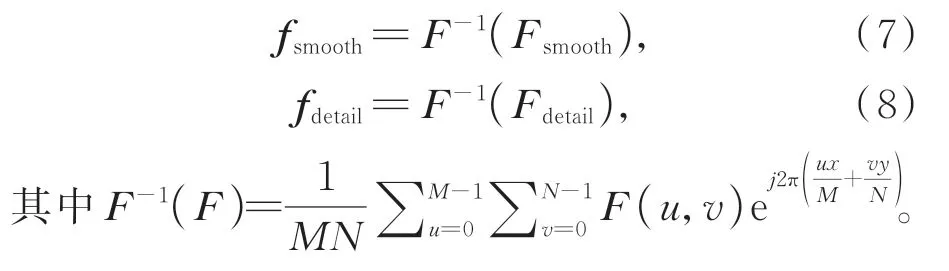
3 基于分區的多正則化圖像復原算法

正則化圖像復原的目標函數模型求解問題可描述為：

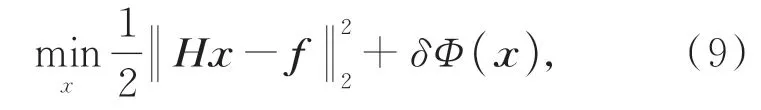
針對集成電路X射線圖像噪聲強烈、對比度低的特點，本文提出一種多正則化圖像復原方法。該方法充分考慮圖像邊緣細節和圖像平滑區域在細節保持和噪聲去除上的不同需求，設計了一種TV-l1范數的混合正則化模型，如式（10）所示：

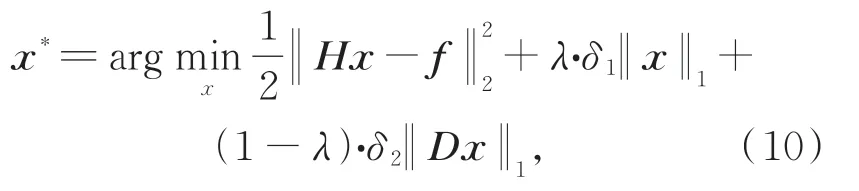
其 中：δ1和δ2為 正 則 化 參 數，D為 梯 度 算 子，‖Dx‖1為TV正則化項，如式（11）～（12）所示。λ為觀測圖像選擇因子，當f是高頻對應的圖像邊緣細節結果時，λ=1；當f是低頻對應的圖像平滑濾波結果時，λ=0。

若‖Dx‖1為各向同性TV，則：

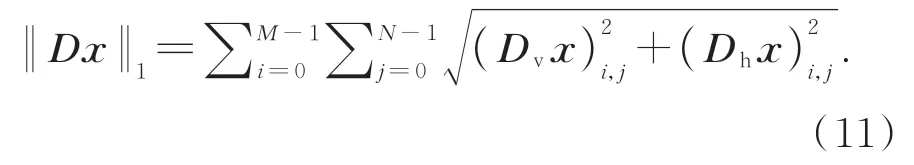
若‖Dx‖1為各向異性TV，則：

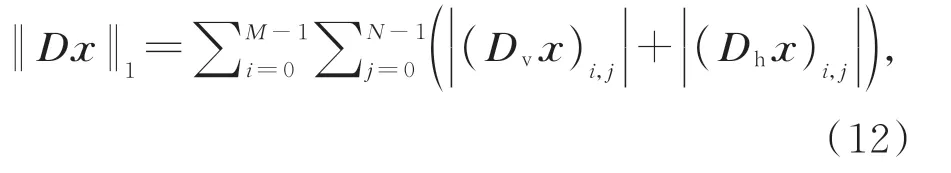
其 中：(Dhx)i，j=xi，j-xi，j-1，(Dvx)i，j=xi，jxi-1，j，Dh表示水平梯度（Horizontal gradient），Dv表示垂直梯度（Vertical gradient），xi，-1=xi，N-1，x-1，j=xM-1，j，（i=0，1，2，…，M-1，j=0，1，2，…，N-1）。

當f是高頻對應的圖像邊緣細節結果時，f=fdetail，λ=1，問題（10）轉化為求解l2-l1問題：

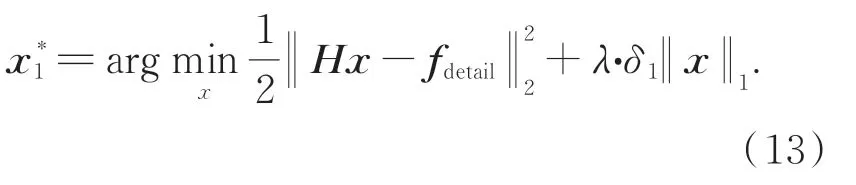
本文采 用GPSR-Basic方法［17］進 行求解，步驟如下：

第 一 步，令x=a-b，a≥0，b≥0，將 問 題（13）轉化為無約束優化問題。

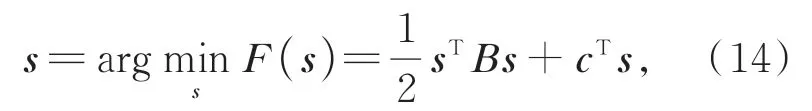
第二步，梯度投影迭代更新。

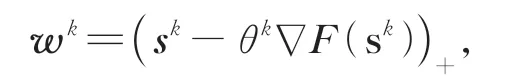
其中(*)+=max(*，0)，θk＞0。

第三步，回溯線搜索θ1∈(0，1)。

若 滿 足F(wk)≤F(sk)-θ1?F(sk)T(skwk)，則令sk+1=wk。

最后，判斷截止條件，若：

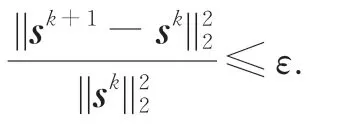
則sk+1=s*，xdetail=a*-b*，否則返回第二步。

若f是低頻對應的圖像平滑濾波結果時，f=fsmooth，λ=0，則問題（10）轉化為求解l2-TV問題（15），

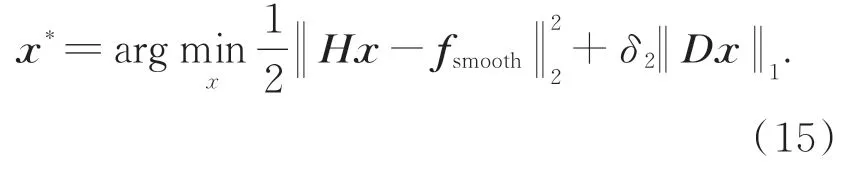
結合微分空間在梯度細節保持上的優越性，本文采用文獻［16］的D-ADMM（Derivative Alternating Direction Method of Multipliers）進行求解，力求平滑區域在平滑去噪的同時保留更多的微小細節信息，避免過渡平滑帶來的集成電路X射線圖像的細節損失。

通過微分空間和圖像空間的等效條件，問題（15）轉化為：

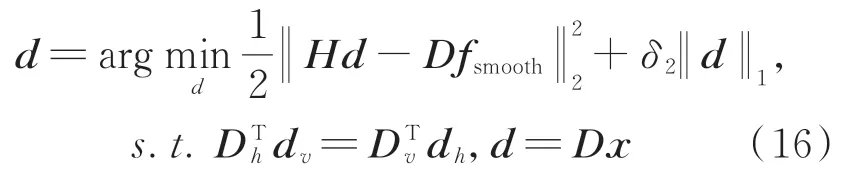
令z=d，由增廣拉格朗日方法，問題（16）轉化為無約束優化問題，

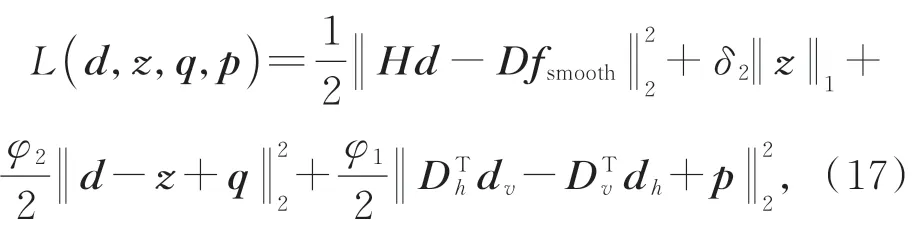
其 中：d=[dTh，dTv]T，dh=Dh x，dv=Dv x，z=

在ADMM框架下（17）可以轉化為多個簡單的子問題進行求解，具體如下：

第一步，求dk+1h，dk+1v：

v+φ2I，Ch=表示按像素相除（entry-wise division）。其中：Bv=HTH+φ1Dh DTh+φ2I，Cv=

第二步，更新zk+1：

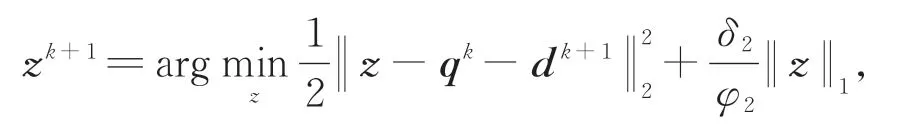
對于各向同性TV，有：

對于各向異性TV，有：

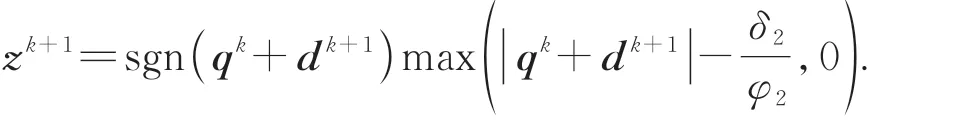
第三步，更新pk+1，qk+1：

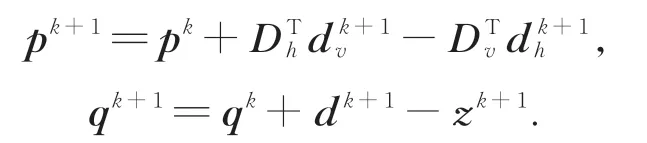
最后，判斷截止條件。

若滿足如下條件：

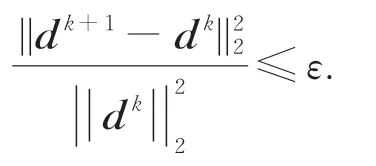
則得到復原圖像xsmooth=U(dk+1)=U(d*)。

若條件不滿足則跳轉至第一步，k=k+1。

綜合高頻對應的圖像邊緣細節復原結果和低頻對應的圖像平滑部分復原結果得到期望的集成電路X射線圖像復原結果，獲得噪聲去除和細節保持的有效平衡。

4 實驗與結果分析

為了驗證本文算法的有效性，采用標準自然光圖像和集成電路的X射線圖像進行兩個系列的實驗驗證。實驗的軟硬件實驗環境為：Matlab（R2016b），Inter（R）Core（TM）i5-8250U CPU@1.60 GHz，8 GB內 存。X射 線 成 像 示 意 圖 及本文采用的X射線設備如圖1所示。

圖1 X射線成像示意圖及本文采用的X射線設備Fig.1 X-ray imaging schematic diagram and X-ray equipment used in this paper

4.1 標準灰度圖像實驗驗證

該 實 驗 采 用Boat，Cameraman，Lena，Peppers 4幅經典的自然光圖像進行實驗驗證，原圖如圖2所示。實驗參數如下：噪聲方差為μ=5×10-3，經驗系數β=0.72，正則化參數δ1=9×10-4，δ2=9×10-5，截止條件ε=10-5。

圖2 標準灰度圖像Fig.2 Standard grayscale images

本文采用均方誤差（MSE），峰值信噪比（PSNR），結構相似性（SSIM）對4幅圖像的復原結果進行分析，如表1所示。顯然，本文方法的去噪指標MSE、PSNR和細節保持指標SSIM均優于對比算法，表明本文方法的復原結果得到了噪聲去除和細節保持的有效平衡，因此可將其用于集成電路的X射線圖像復原。

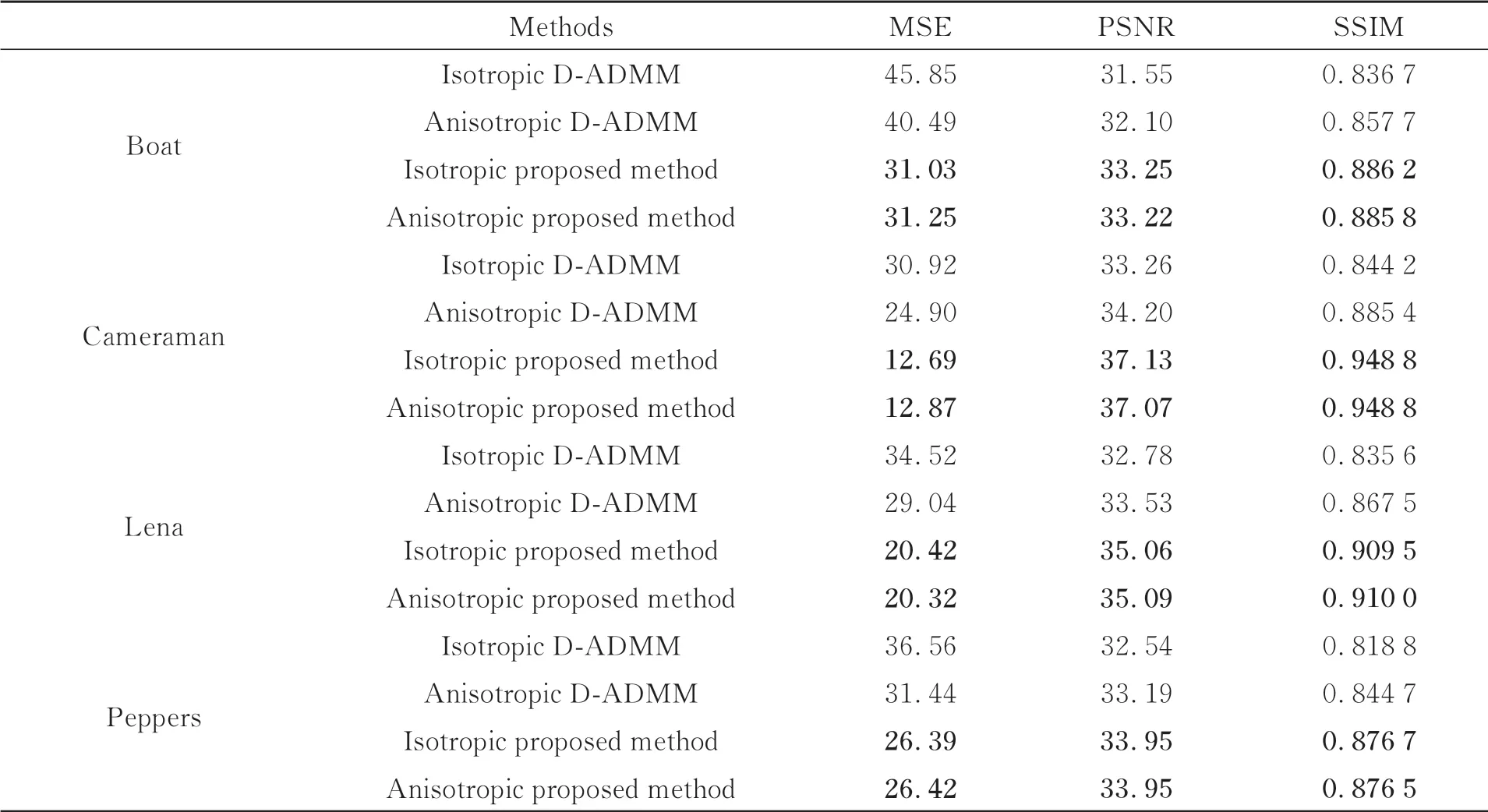
表1 標準灰度圖像實驗結果Tab.1 Experimental results of standard gray images

4.2 集成電路X射線圖像實驗驗證

集成電路的X射線圖像選擇電容元件、焊點等3幅圖像進行驗證。實驗參數選擇為β=0.72，正 則 化 參 數δ1=2×10-5，δ2=8×10-4，截止條件ε=10-5。

圖3～圖5所示為三幅圖像的復原結果，對比方法為文獻［4］所述的混合去噪方法、各向同性D-ADMM和各向異性D-ADMM。顯然，各方法均可獲得集成電路X射線圖像的有效復原，但是，本文方法的復原結果對比度高，邊緣更加清晰。圖中放大顯示的細節部分表明本文方法能夠更清晰地展示電容條狀結構、焊點氣泡邊緣等細節信息，進一步表明了本文方法在噪聲去除的同時具有更好的細節保持效果，為后續缺陷檢測、提高產品可靠性奠定基礎。

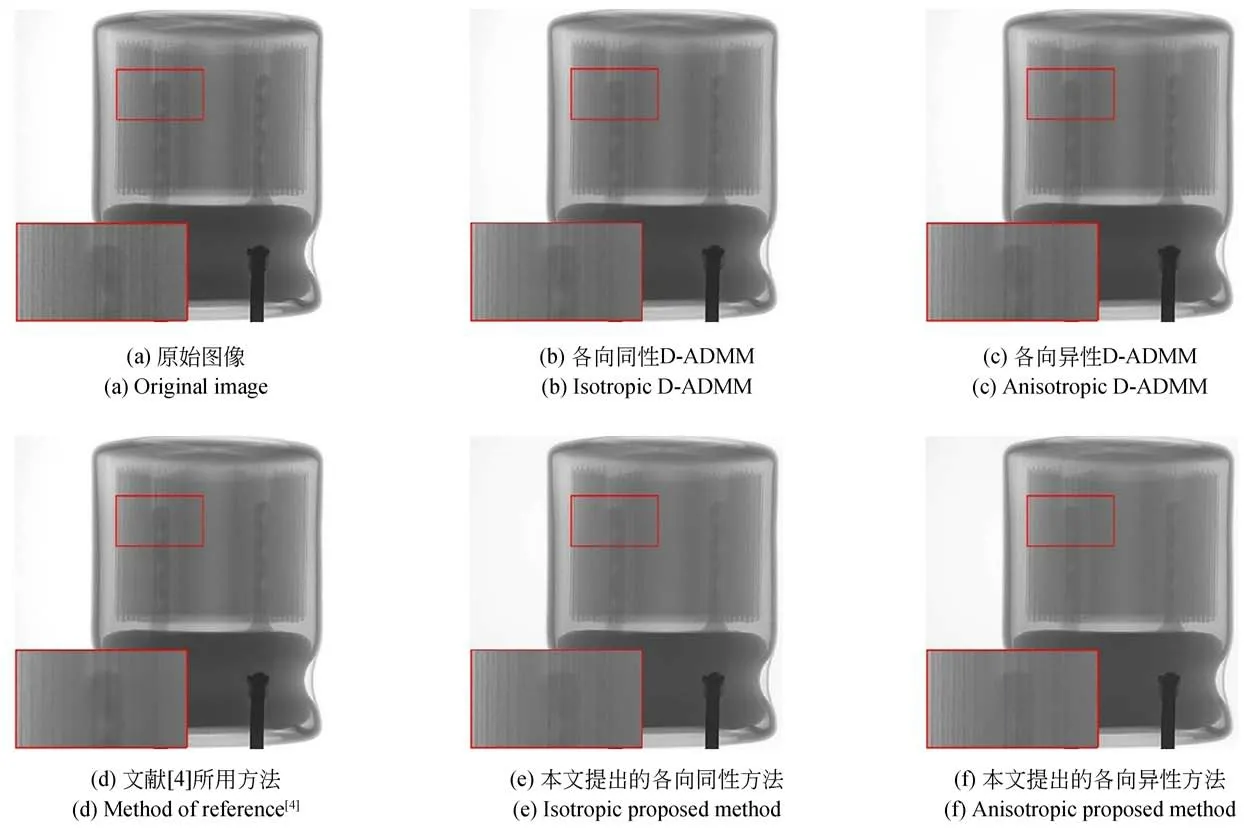
圖3 電容元件圖像復原結果Fig.3 Restored results of capacitance element image

圖5 焊點2圖像復原結果Fig.5 Restored results of welding spot 2

圖4 焊點1圖像復原結果Fig.4 Restored results of welding spot 1

為更進一步驗證本文算法的優越性，本節計算出以上復原結果的拉普拉斯梯度（Laplacian Sum，LS），灰度平均梯度（Gray Mean Grads，GMG），邊緣強度（Edge Intensity，EI）對X射線圖像的復原結果進行客觀評價，如表2所示。實驗結果表明本文算法在去除噪聲的同時能夠保留更多的細節信息。

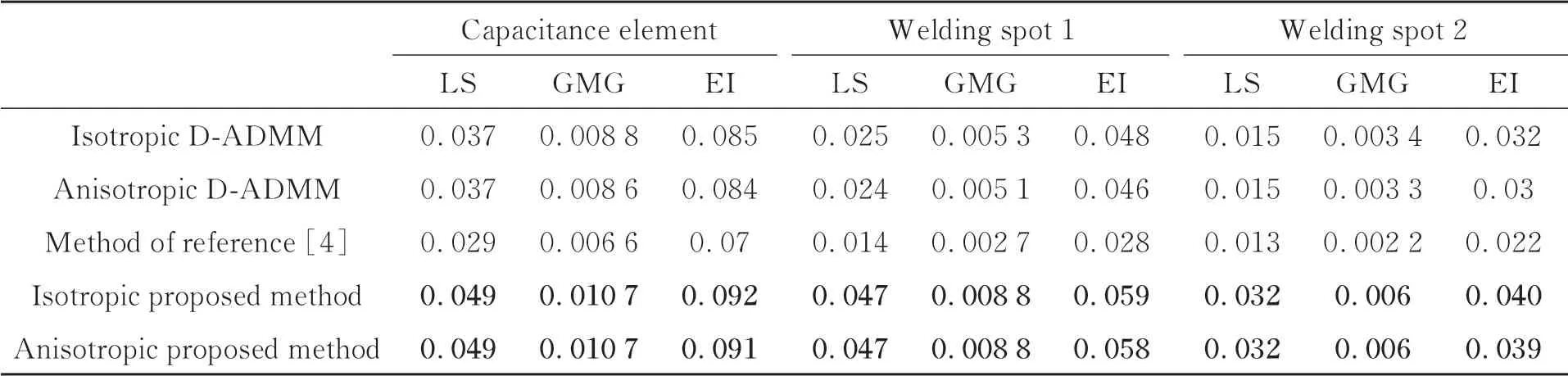
表2 3幅集成電路X射線圖像實驗結果Tab.2 Experimental results of three integrated circuit X-ray images

隨后，本文對另10幅集成電路的X射線圖像進行了實驗驗證，客觀評價如表3所示，再次驗證 了本文方法的有效性。

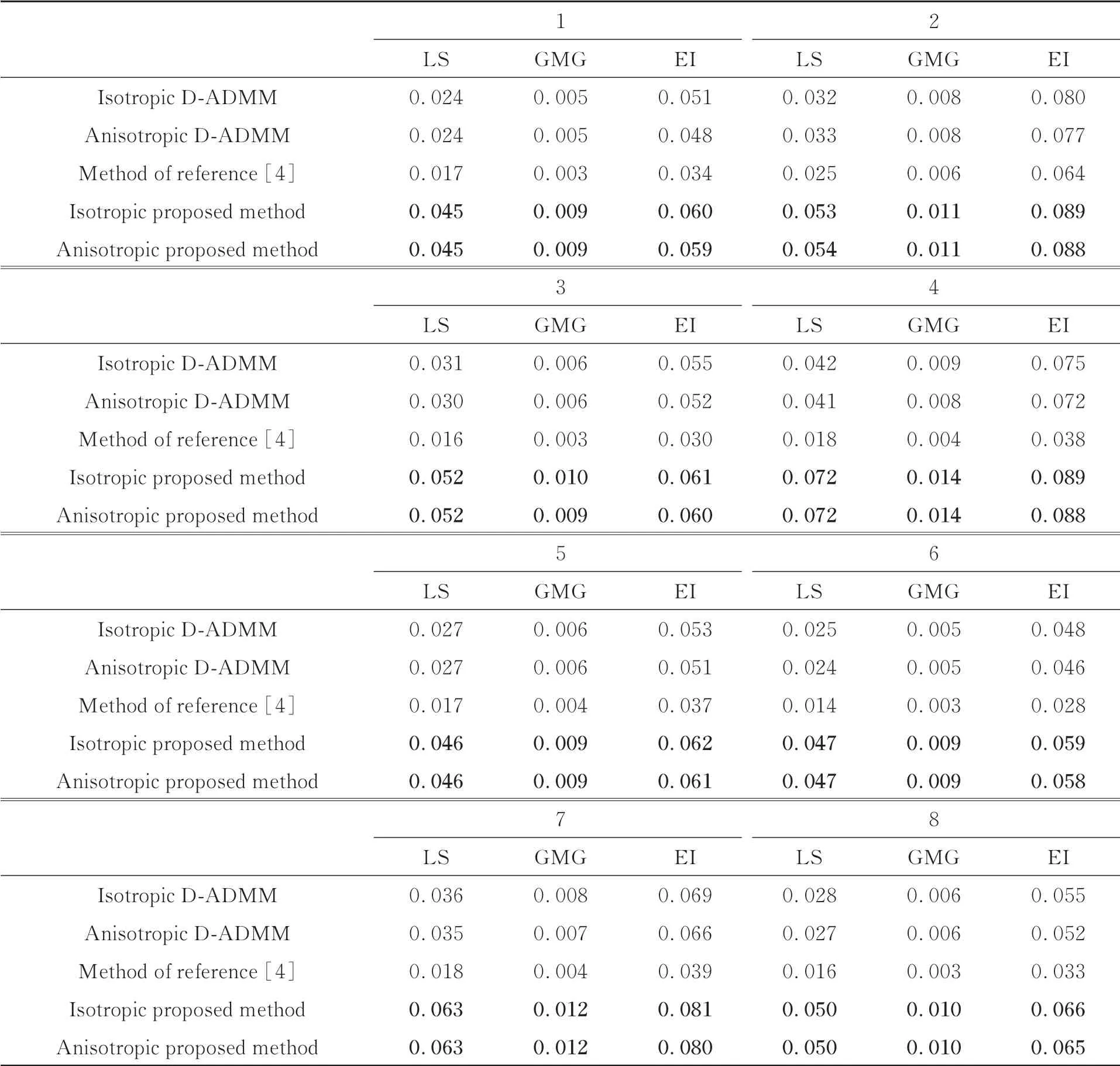
表3 另10幅集成電路X射線圖像實驗結果Tab.3 Another ten integrated circuit X-ray images experimental results

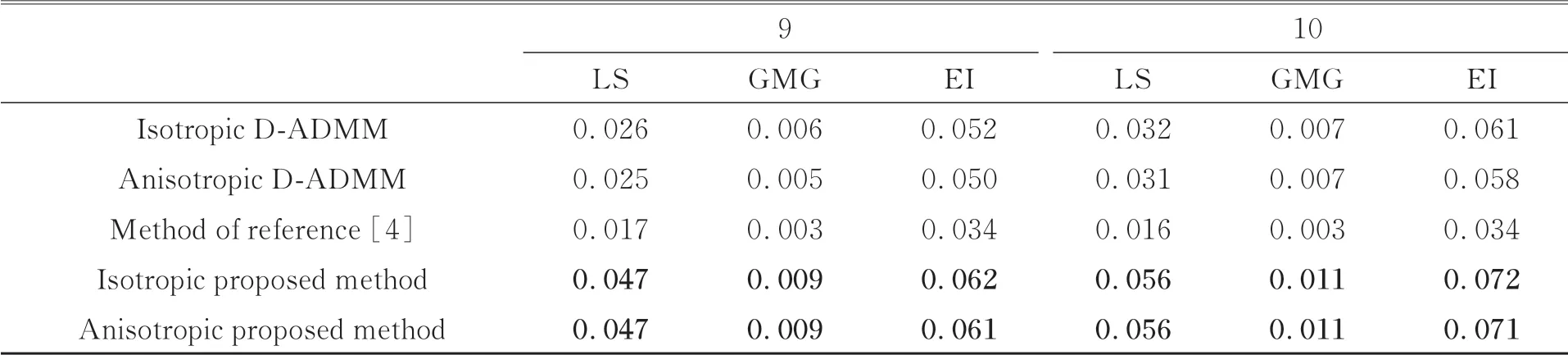
續表3另10幅集成電路X射線圖像實驗結果Tab.3 Another ten integrated circuit X-ray images experimental results

5 結論

本文在分析集成電路X射線成像特點的基礎上，提出了一種多正則化集成電路X射線圖像復原算法。首先，通過高斯高通濾波和高斯低通濾波獲取圖像的高頻邊緣細節結果和低頻平滑濾波結果并以此作為圖像復原的觀測圖；然后提出了一種l1-TV混合正則化圖像復原模型。該模型充分考慮了邊緣細節和平滑部分的復原需求，解決了整幅圖像采用單一正則化項造成的細節過度平滑缺失或去噪效果差的問題。實驗表明本文方法的復原結果對比度高，邊緣清晰，在集成電路X射線圖像復原中獲得了去噪和細節保持的有效平衡，可為后續缺陷檢測、提高產品可靠性奠定基礎。