基于DTW相似度和Bi-LSTM的滾動軸承壽命預測

周建清，朱文昌，王恒

(1.常州市高級職業技術學校電氣工程學院，江蘇常州 213161；2.南通大學機械工程學院，江蘇南通 226019)

0 前言

滾動軸承作為機械設備的核心部件，其性能好壞直接影響設備能否正常運行，因此，在軸承損壞前預測其剩余使用壽命，避免設備損壞造成的財產損失及人員傷亡，具有重大研究價值[1-2]。

近年來，以數據驅動為主的深度學習算法在滾動軸承壽命預測方面得到了廣泛的應用，主要圍繞2個問題展開：(1)選擇合適的深度學習算法或對深度學習算法進行優化，提高預測的準確率；(2) 構造出單調性好、對軸承異常敏感的退化指標訓練神經網絡，使其充分挖掘并學習軸承的退化信息以提高預測精度。在滾動軸承壽命預測算法選擇方面，目前以長短期記憶神經網絡(Long Short-Term Memory,LSTM)為代表的深度學習算法得到了廣泛應用。劉小勇[3]根據滾動軸承原始數據構建退化指標，將退化指標作為LSTM網絡的輸入，完成對滾動軸承壽命的預測，并驗證了深度學習算法與傳統的機器學習算法相比具有更高的預測精度。NGUYEN和MEDJAHER[4]利用LSTM進行壽命預測,給出了系統在不同時間窗下的故障概率,以平均成本率為標準,獲得了比周期性預測策略和理想預測維護策略更好的結果。WANG等[5]對LSTM預測算法進行了改進，將雙向長短時記憶網絡 (Bi-directional Long Short-Term Memory,Bi-LSTM) 應用于負荷的短期預測并取得了很好的試驗效果。在構建軸承退化指標的研究中，孟文俊等[6]提取滾動軸承時域、頻域特征并通過主成分分析進行融合，但構造出的融合指標單調性較差，數據波動較大；韓林潔[7]利用單卷積神經網絡(Convolutional Neural Network,CNN)提取出滾動軸承的退化信息，輸入進門控循環單元(Gated Recurrent Unit,GRU)實現了軸承的壽命預測，但單卷積神經網絡提取出的特征較為單一，容易造成信息損失；胡城豪等[8]提出一種多尺度卷積神經網絡，克服了單卷積神經網絡的問題，但卷積神經網絡中的卷積核個數及卷積核大小的設定依靠經驗而定，缺乏一定的科學性。信息熵指標作為一種傳統退化指標，可用于量化信息的不確定度，具有較好的魯棒性及穩定性，被廣泛應用于軸承故障診斷[9]、退化評估[10]及壽命預測[11]中，然而信息熵對軸承異常不敏感，難以準確刻畫軸承的退化歷程[12]。動態時間規整算法(Dynamic Time Warping,DTW)可用于計算時間序列的相似度，通過對時間序列進行伸縮、對齊及規整等操作可準確描述時間序列間的相似度與差異性。NGUYEN[13]利用DTW算法計算時間序列間的相似性并進行狀態匹配，與歐幾里得距離相比，它對時間序列相似度的計算更為準確。LI等[14]利用DTW算法分析手語運動軌跡間的相似性，判斷它們是否屬于同一類別，提高了手語軌跡識別的準確率。將DTW用于計算信息熵指標間的相似度，實現對信息熵指標優化的目的，進一步提高該指標對軸承異常的敏感程度。

綜上，本文作者用動態時間規劃算法優化信息熵指標，將相似度作為滾動軸承健康指標，結合Bi-LSTM實現滾動軸承壽命的預測，結果表明了該方法的有效性和可行性。

1 滾動軸承健康指標的構建

1.1 基于信息熵的軸承特征提取

根據軸承健康監測信號采集特點，在監測時間T內傳感器共采集軸承信號M次，每次采集到N個數據點，每個點記為x(m,n)，故tm時刻采集到的數據刻構成列向量x(tm)：

x(tm)=[x(m,1),x(m,2),…,x(m,n),…,x(m,N)]T1≤m≤M,1≤n≤N

(1)

通過M次采集到的軸承數據X=[x(t1);x(t2);…;x(tm);…;x(tM)]為二維數據集合，其第一維是時間維度，記錄軸承從正常到失效的整個過程；第二維為空間維度，記錄同一時刻下軸承不同位置的狀態信息。由于不同時刻采集到的軸承數據具有不同的分布特性，基于此特性本文作者采用信息熵提取不同時刻軸承信號的分布特征。

1984年SHANNON提出了信息熵的概念用來解決對信息的量化度量問題[15]。在信息論中，一個系統越穩定，其信息熵越小，tm時刻軸承信息熵的計算如式(2)所示：

(2)

式中：P[x(m,n)]表示x(m,n)出現的概率。

在監測時間T內計算出不同時刻的信息熵，得到退化特征序列F:

F=[S(t1),S(t2),…,S(tm),…,S(tM)]

(3)

雖然信息熵可表征數據整體的分布特性，但由于相鄰時間段間熵值信號變化較為微弱，難以準確表征滾動軸承退化的各個階段，需對它進行優化處理。

1.2 基于DTW的滾動軸承健康指標構建

滾動軸承的退化具有連續性及不確定性，軸承當前退化狀態雖與前n個狀態有關，但當前軸承的前后兩個退化狀態具有較大差異性，并隨著退化的加劇，正常狀態、早期異常及嚴重故障狀態下的數據間的差距將逐漸增大，通過分析不同時間段下數據的差異性可更好地描述軸承的退化狀態，動態時間規整算法能準確計算出時間序列間的相似性(差異性)。利用DTW算法優化信息熵指標，計算不同階段熵值指標的相似度，將它作為健康指標，用于表征軸承的退化歷程。

在計算相似度之前，選定軸承正常狀態下的時間序列作為參考模板P，同時利用時間窗遍歷軸承退化序列F構造測試模板Q，設置時間窗規模為1×g，對退化序列F進行信息鎖定。在采樣時刻tm下構造出的測試模板為

Q(tm)=[S(tm-g),S(tm-g+1),…,S(tm-1),S(tm)]

(4)

設定參考模板P不變，測試模板Q隨時間tm而改變，計算兩者間的相似度，并用于反映當前軸承退化狀態與正常狀態間的差異性。由于DTW算法在時間序列間相似性計算方面更優，故將相似度作為健康指標可更好地表征軸承的退化歷程。

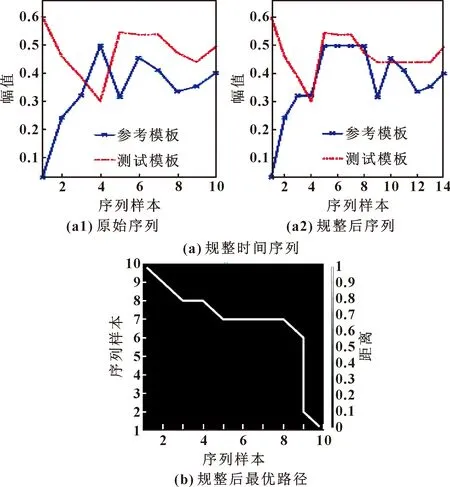
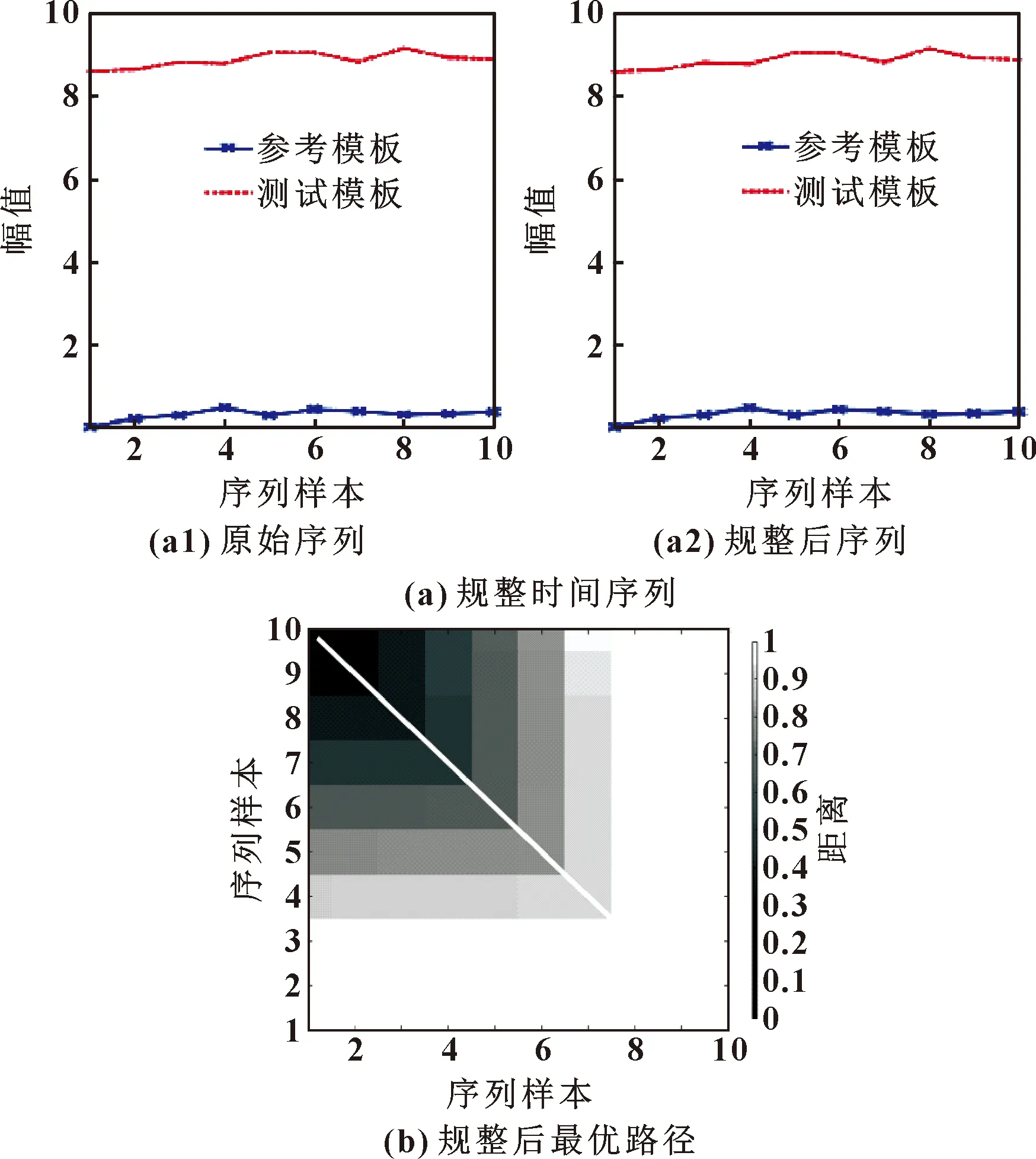
假設構造出的參考模板為P=[p1,p2,…,pl,…,pL](1

(5)

當w遵循邊界性、單調性及連續性的約束時[16]，P和Q之間所有對齊路徑的集合記為AP,Q。DTW算法的目標是最小化兩條時序數據中所有對應數據點的局部距離之和，其定義如式(6)所示：

(6)

DTW算法采用動態規劃思想，利用遞歸公式(6)將以上問題轉換為對P和Q子序列問題的求解：

(7)

通過計算路徑的距離可有效實現軸承的不同序列模板間數據的相似性，相似性越大則距離越小，利用它對信息熵退化指標進行優化并構建健康因子。

1.3 基于Bi-LSTM的軸承壽命預測

雙向長短期記憶網絡是對長短期記憶神經網絡的一種延伸，它由一個前向LSTM與一個后向LSTM組成，能夠對輸入數據進行正向和反向遍歷[17]。LSTM模型如圖1所示。

由圖1可知，每個LSTM單元都配有3個控制信息流的門，每個門均包含一個激活函數和一個逐點乘法運算。遺忘門控制信息流;輸入門決定哪些信息比較重要以便記憶；輸出門決定將要傳遞的信息。3個門的值設置在0和1之間。其工作步驟如下：

(1)遺忘門決定應該記住或遺忘哪些信息，如式(8)所示：

ft=σ(Wf[at-1,xt]+bf)

(8)

式中：at-1表示上一時刻的隱層信息；xt表示當前輸入；Wf與bf分別表示LSTM網絡的權值和偏置，均為模型訓練參數；σ表示激活函數sigmoid。

圖1 LSTM模塊示意

(2)輸入門確定需要保存的信息，如式(9)所示：

Ct=ft*Ct-1+σ(Wi[at-1,xt]+

bi)*tanh(Wc[at-1,xt]+bc)

(9)

式中：Ct-1為前一個細胞的狀態;Ct為當前細胞狀態信息。

(3) 輸出門決定要傳遞的信息，如式(10)所示：

at=σ(Wo[at-1,xt]+bo)*tanh(Ct)

(10)

Bi-LSTM神經網絡在LSTM網絡的基礎上進行了改進，每個訓練模塊的輸出層都包含一個前向LSTM和一個反向LSTM網絡，如圖2所示。其輸出包括上下文的特征信息，理論上較LSTM可提高預測的準確度[18]，文中采用Bi-LSTM對滾動軸承剩余壽命進行預測。

圖2 Bi-LSTM模塊示意

綜上所述，本文作者基于信息熵及DTW算法構造出滾動軸承健康指標用于表征軸承的退化狀態，結合Bi-LSTM網絡可實現軸承壽命的預測，其算法流程如圖3所示，具體步驟為：

(1)利用信息熵提取滾動軸承的時域退化特征；

(2)提取退化指標F的正常時間序列作為參考模板P，利用時間窗遍歷指標F不同時刻的退化信息并構造測試模板Q，利用DTW算法計算相似度，并將它作為健康指標用于表征軸承的退化；

(3)將優化后的指標分為測試集及訓練集，訓練Bi-LSTM網絡并預測軸承壽命。

圖3 文中所提算法流程

2 應用研究

2.1 數據來源

試驗數據來自法國IEEE PHM 2012 Prognostic challenge提供的公開數據集，試驗裝置如圖4所示，采集到的試驗數據分為訓練數據及測試數據，取Bearing1_1軸承訓練數據集的水平振動加速度信號進行分析，試驗軸承轉速為1 800 r/min，所受載荷為4 000 N，傳感器采樣頻率為 25.6 kHz，采樣間隔為10 s，當振動加速度信號幅值達到20g時軸承失效，此過程共采集到2 803組數據。

圖4 軸承加速度壽命試驗裝置

對Bearing1_1軸承數據按上文所述方法進行處理，取熵值指標正常狀態下的時間序列為參考模板，測試模板與參考模板中特征矢量長度均為10。利用Bi-LSTM算法預測軸承壽命時，設定Bi-LSTM網絡含有兩個LSTM層，隱含層神經元個數為50，激活函數為Relu，ADAM用于梯度優化，輸入層節點數為10，輸出層為1，學習率為0.01。

2.2 滾動軸承健康因子構建

按照第1節所述方法對Bearing1_1數據集進行處理，構造出的熵值指標與傳統峭度指標相比，熵值曲線單調性較好，所受的擾動更小，魯棒性較強，但其變化較微弱，無法明顯辨識軸承早期異常的發生，難以準確區分軸承退化的不同階段，如圖5所示。

圖5 軸承Bearing1_1的熵值指標及峭度指標

為提高指標的表征性能，采用DTW算法對其進行優化，提取110～200 s的信息熵指標作為參考模板，分別提取210～300 s與26 010～26 100 s的熵值指標作為測試模型進行相似度的計算。當提取210～300 s的熵值作為測試模板計算其余參考模板間的相似度時，DTW算法先對兩個序列的各個點進行縮放及對齊處理，如圖6(a)所示。在進行路徑規整后，最優路徑從數量較小的深色區經過，路徑的累計距離即為兩個序列間的相似度(圖6(b))，此時累計距離較小為0.563。這是由于兩個序列都處于正常狀態，雖然原始序列間存在一些細微的差距，但是所蘊含的軸承退化信息較為相似，通過DTW算法縮放、對齊及規整后兩序列基本一致，累計距離較小。在參考模板不變的情況下，選定26 010～26 100 s的特征序列作為測試模板計算相似度時，由于參考模板與測試模板間差異較大，DTW算法無法將兩模板對齊，最終規整后的路先經過淺色區域，累計距離較大為24.785，如圖7所示。利用此算法對信息熵退化指標不同階段數據進行遍歷，計算其相似度，可構建出如圖8所示的健康指標。健康指標在19 180 s之前整體較為穩定，在此時刻之后，曲線整體有較為明顯的上升趨勢，故將此時刻定義為Bearing1_1的早期異常點。與圖5中的峭度指標與信息熵指標相比，經過相似度優化后的健康指標能更明顯檢測出軸承異常的發生，證明該方法有效性。

圖6 210～300 s軸承相似度計算

圖7 26 010～26 100 s軸承相似度計算

圖8 基于DTW優化后的健康指標

2.3 基于Bi-LSTM的軸承壽命預測

第2.2節中構建出了滾動軸承的健康指標并檢測到軸承在19 180 s后進入退化狀態，提取0～19 180 s的健康指標對Bi-LSTM算法進行訓練，并用訓練好的網絡對19 180 s后的軸承數據進行滾動軸承壽命的預測，結果如圖9所示。

圖9 基于健康指標及Bi-LSTM的軸承壽命預測

為驗證所提出的方法(Entropy-DTW-Bi-LSTM)的準確性，將它與Entropy-DTW-LSTM算法、Entropy-Bi-LSTM算法及Entropy-LSTM算法進行對比試驗，取均方誤差(Mean Squared Error,MSE)與相關指數R2對其進行評價，如公式(11)所示：

(11)

式中：fpred,i為第i個序列對應的預測值;fact,i為第i個序列對應的真實值;fmean為真實值的均值。

在LSTM網絡隱藏層神經元個數、學習率、激活函數等網絡參數不變的情況下，對比上文中提到的幾種算法的預測結果，如表1所示。可知：文中所提出的滾動軸承壽命預測算法預測結果的eMSE更小、相關指數R2值更大，更為接近真實壽命曲線。同時，當基于數據驅動的滾動軸承壽命預測算法難以明顯提高壽命預測精度時，通過改變軸承健康指標的性能，提高其單調性及對異常點敏感性可有效提高算法預測的精度。

表1 各模型預測結果對比

3 結論

本文作者通過DTW算法研究滾動軸承不同階段下熵值指標時間序列間的相似性，構造軸承健康指標結合Bi-LSTM算法，實現了軸承異常的檢測及壽命的評估，得出以下結論：

(1)與傳統指標相比，基于DTW算法優化信息熵值指標后構造出的健康指標的單調性及魯棒性較強，且對軸承的早期異常更敏感，為軸承狀態退化評估提供了一種新的研究方法；

(2)將DTW優化構建出的健康指標結合Bi-LSTM的壽命預測算法與其他預測方法相比，當基于數據驅動的算法難以明顯提高軸承預測精度時，通過優化健康指標可進一步提高預測效果。