分?jǐn)?shù)階傅里葉變換聯(lián)合支持向量機的建筑物變形預(yù)測

古 巍 李 倩 陳代果

1 四川大學(xué)錦江學(xué)院, 四川省眉山市錦江大道1號, 620860 2 西南科技大學(xué)土木工程與建筑學(xué)院，四川省綿陽市青龍大道中段59號,621010

目前，建筑物變形預(yù)測方法以統(tǒng)計學(xué)方法和人工智能算法為主。其中，統(tǒng)計學(xué)方法是在對變形數(shù)據(jù)進行分析處理的基礎(chǔ)上，提取其中的規(guī)律性信息，并利用確定的數(shù)學(xué)模型對其建模，常用的有ARMA、ARIMA等時間序列模型及灰色理論模型和卡爾曼濾波等[1-2]。不同于統(tǒng)計學(xué)方法，人工智能算法不需要建立精確的數(shù)學(xué)模型，直接采用數(shù)據(jù)驅(qū)動的方式將時間序列中的變形信息轉(zhuǎn)化為網(wǎng)絡(luò)結(jié)構(gòu)參數(shù)，通過自適應(yīng)自學(xué)習(xí)能力對未來的變形趨勢進行預(yù)測，經(jīng)典的人工智能算法包括反向傳播(back propagation, BP)神經(jīng)網(wǎng)絡(luò)[3]、長短時記憶神經(jīng)網(wǎng)絡(luò)(long short-term memory neural network, LSTM)[4]和支持向量機(support vector machine, SVM)[5]等方法。其中，BP神經(jīng)網(wǎng)絡(luò)具有任意非線性函數(shù)逼近能力，其預(yù)測性能優(yōu)于時間序列模型；而SVM采用核函數(shù)的方式將低維空間中的非線性問題轉(zhuǎn)化為高維空間中的線性問題，從而提升模型的計算效率及對小樣本、非線性問題的適應(yīng)能力。但BP神經(jīng)網(wǎng)絡(luò)和LSTM神經(jīng)網(wǎng)絡(luò)的預(yù)測性能受網(wǎng)絡(luò)初值影響較大，且對噪聲敏感[6]。

針對建筑物變形數(shù)據(jù)非平穩(wěn)和波動性特征，本文基于分解-預(yù)測-重構(gòu)的思想，提出一種基于分?jǐn)?shù)階傅里葉變換(FrFT)和支持向量機(SVM)的組合預(yù)測模型，用于建筑變形趨勢預(yù)測。實驗結(jié)果表明，該組合模型相對于單一預(yù)測模型能夠獲得更高的預(yù)測精度。

1 組合預(yù)測模型

建筑物的變形過程具有非線性、非平穩(wěn)和波動性特征，單一模型無法在預(yù)測過程中準(zhǔn)確捕捉這些信息，因此預(yù)測精度不高，且噪聲穩(wěn)健性較差。本文結(jié)合FrFT處理非平穩(wěn)時間序列的優(yōu)勢和SVM對小樣本、非線性問題的泛化能力，提出一種FrFT-SVM建筑物變形組合預(yù)測模型。該組合預(yù)測模型首先利用FrFT將復(fù)雜時間序列分解為多個簡單子序列，同時引入相關(guān)向量機(relevance vector machine, RVM)自動確定最優(yōu)FrFT階次，并利用SVM對每個子序列分別進行建模預(yù)測；同時為了提升預(yù)測性能，提出一種改進的果蠅優(yōu)化算法(improved fruit fly optimization algorithm, IFOA)對SVM核參數(shù)和懲罰因子進行全局尋優(yōu)；最后將每個子序列的預(yù)測結(jié)果進行綜合疊加，得到最終預(yù)測結(jié)果。

1.1 基于FrFT的變形時間序列分解

FrFT又稱為廣義傅里葉變換，在保留傳統(tǒng)傅里葉變換性質(zhì)的同時又具備其特有優(yōu)勢，能夠同時對時域和頻域信息進行分析處理，是非線性、非平穩(wěn)時間序列分析的強有力工具[7]。

圖1在時間-頻率二維坐標(biāo)平面中給出傳統(tǒng)傅里葉變換和FrFT之間的關(guān)系示意圖，其中橫坐標(biāo)代表時間t，縱坐標(biāo)表示頻率f。傳統(tǒng)傅里葉變換可以看作是將時間軸按逆時針方向旋轉(zhuǎn)π/2，得到頻率軸的一種線性變化，即在(t,f)二維平面內(nèi)的一種時間序列分析手段；而FrFT可以看作是將時間序列沿逆時針方向旋轉(zhuǎn)任意α角度，得到分?jǐn)?shù)譜f(u)和F(v)的過程，隨著α的取值從0變化到π/2，F(xiàn)rFT可以呈現(xiàn)出時間序列從時域向頻域逐漸轉(zhuǎn)變的過程。對于(t,f)平面內(nèi)的非平穩(wěn)信號，通過將其轉(zhuǎn)換到合適的(u,v)平面能夠有效消除交叉項。

圖1 FrFT與傳統(tǒng)傅里葉變換關(guān)系示意圖Fig.1 Schematic diagram of the relationship between FrFT and traditional Fourier transform

對于連續(xù)時間序列f(t)，對其進行p階FrFT變換的表達(dá)式為：

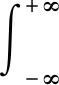
(1)

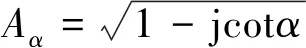
由于實際工程實踐中處理的都是經(jīng)采樣后的離散序列，因此要對式(1)進行離散化處理，從而得到離散分?jǐn)?shù)階傅里葉變換(discrete FrFT, DFrFT)。常用的一種FrFT離散化方法為Ozaktas采樣方法，首先對原始信號進行時域展開，然后根據(jù)Shannon采樣定理進行插值，最后得到FrFT的離散化處理結(jié)果。對式(1)展開得：

(2)

利用Shannon定理對式(2)中積分項f(t)exp[jπt2cotα]進行插值處理，可將其轉(zhuǎn)化為：

(3)

最后，將式(3)代入式(2)，得到原始時間序列f(t)的p階DFrFTfp(m)為：

(4)

式中，n和m分別為原始時間序列和p階DFrFT的采樣點數(shù)，N為時間序列總長度，1/Δx為時間序列采樣間隔。

1.2 最優(yōu)FrFT階次的確定

根據(jù)式(1)～式(4)，當(dāng)DFrFT階次p=0時，得到的結(jié)果為原始時間序列；當(dāng)p=1時，得到的結(jié)果為原始時間序列的頻譜。利用DFrFT進行時間序列分析時，通常將p的取值在0.1～0.9范圍內(nèi)按0.1間隔進行遍歷，分別得到不同階次的DFrFT結(jié)果。遍歷方法雖然簡單，但是得到的DFrFT中有些階次會獲得較好的時-頻能量聚集特點，能夠有效反映時間序列的趨勢性和周期性等有用信息，另外一些階次(例如噪聲分量)能量會均勻分布在整個平面內(nèi)，不包含對趨勢預(yù)測的有用信息，因此需要一種方法能夠自動確定DFrFT中的最優(yōu)階次。

相關(guān)向量機(relevance vector machine, RVM)是一種貝葉斯框架下的最優(yōu)分類器，與SVM類似，RVM同樣采用核函數(shù)的方式將低維空間中的非線性問題映射為高維空間中的線性問題，但同時又具備特有的優(yōu)勢：1)RVM通過引入共軛先驗分布的方式增加了模型的稀疏性，因而具有自動特征選擇能力；2)RVM模型將特征選擇與分類器設(shè)計統(tǒng)一為同一個優(yōu)化問題，具備更強的泛化能力；3)RVM能夠提供概率式預(yù)測結(jié)果，相當(dāng)于提供了更多的信息；4)RVM核函數(shù)的選擇不受摩西準(zhǔn)則約束。

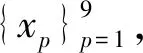
(5)

式中，K(x,xp)為核函數(shù)，wp代表不同的權(quán)重，ε為0均值高斯白噪聲(方差為τ-1)。

RVM通過向分類模型中引入Sigmoid函數(shù)的方式實現(xiàn)對目標(biāo)值的概率預(yù)測，此時輸入特征向量的似然函數(shù)可以表示為：

p(t|w)=

(6)

式中，tp為xp對應(yīng)的類別標(biāo)號。

為了構(gòu)建完整的貝葉斯框架，對模型權(quán)值wp引入先驗分布，常用的分布形式為高斯分布，即假設(shè)wn服從0均值、方差為α-1的高斯分布。由于高斯分布的共軛先驗分布為伽馬分布，因此采用伽馬分布定義α-1和τ-1的超先驗值：

(7)

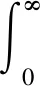
上述RVM模型常用的求解方法為變分貝葉斯期望最大(variational bayesian expectation maximization, VBEM)算法[8]，在求解過程中會發(fā)現(xiàn)，大部分α?xí)S著迭代的進行逐漸趨于無窮大，對應(yīng)的w則趨于0，從而實現(xiàn)了權(quán)值向量的稀疏化；迭代終止時，不為0的權(quán)值對應(yīng)的特征向量即為要選擇的特征。

1.3 改進的IFOA-SVM預(yù)測模型

對FrFT分解得到的子序列建立SVM回歸模型并進行預(yù)測，SVM回歸模型具有預(yù)測精度高、算法復(fù)雜度低及適合于小樣本應(yīng)用等眾多優(yōu)點，利用SVM對變形時間序列進行回歸預(yù)測的模型可以表示為：

y=ωTφ(x)+b

(8)

式中，φ(x)為非線性映射函數(shù)，ω為權(quán)值，b為線性偏移量。

SVM采用結(jié)構(gòu)風(fēng)險最小化準(zhǔn)則，將式(8)中模型參數(shù)ω和b的求解過程轉(zhuǎn)化為如下優(yōu)化問題：

(9)

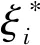
采用拉格朗日乘子法將式(9)轉(zhuǎn)化為：

(10)

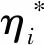
(11)

式中，γ為核參數(shù)。

對式(10)進行求解，可以得到最終的SVM回歸模型：

(12)

SVM回歸模型的預(yù)測精度和泛化能力與懲罰因子c及核參數(shù)γ的取值密切相關(guān)，目前常用的交叉驗證法存在運算量大、自動化程度不高等問題。因此，本文將果蠅優(yōu)化算法(fruit fly optimization algorithm, FOA)[9]與SVM相結(jié)合，利用FOA的全局搜索能力對SVM參數(shù)進行尋優(yōu)，提升模型預(yù)測性能。同時，考慮到傳統(tǒng)FOA采用固定搜索步長，在迭代過程中存在靈活性不足的問題，提出自適應(yīng)搜索步長方法對其進行改進，得到IFOA算法。利用IFOA算法對SVM進行優(yōu)化的步驟為：

1)初始化SVM回歸模型，設(shè)定懲罰因子與核參數(shù)的取值范圍。

2)設(shè)置果蠅種群數(shù)量N和最大迭代次數(shù)T，將懲罰因子c和核參數(shù)γ作為果蠅群體的位置坐標(biāo)，即

(13)

3)根據(jù)式(14)隨機賦予果蠅個體搜尋食物的方向和位置：

(14)

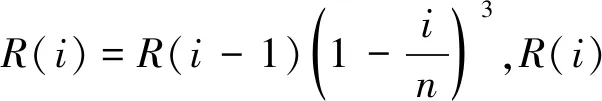
4)計算當(dāng)前果蠅個體與原點之間的距離Di及對應(yīng)味道濃度判定值Pi：

(15)

5)利用Pi計算得到果蠅所在位置的味道濃度值Si，將當(dāng)前果蠅群體中味道濃度值最小的果蠅作為最優(yōu)個體，并記錄Si和對應(yīng)的位置坐標(biāo)[Xi,Yi]。

6)重復(fù)上述步驟，并記錄每次迭代過程中最優(yōu)個體的味道濃度值和空間位置信息，即

(16)

式中，(Xi_best,Yi_best)為第i次迭代果蠅群體中最優(yōu)個體所處位置，Si_best為對應(yīng)的味道濃度值。

7)當(dāng)?shù)螖?shù)達(dá)到最大值T時，步驟6)記錄數(shù)據(jù)中最小濃度值對應(yīng)的位置信息即為SVM的最優(yōu)參數(shù)組合，即

(17)

1.4 綜合預(yù)測

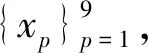
xp=DFrFT(s)p，p=0.1～0.9

(18)

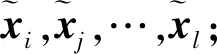
(19)

1.5 組合預(yù)測模型的算法流程

組合預(yù)測模型首先對時間序列進行0.1～0.9階次的FrFT分解，并結(jié)合RVM的稀疏性和特征選擇能力實現(xiàn)對最優(yōu)K個FrFT階次的選取，將原始時間序列轉(zhuǎn)化為K個不同時頻尺度下的子序列，實現(xiàn)序列關(guān)鍵信息的有效提取；然后分別采用SVM對各個子序列進行訓(xùn)練建模，并通過IFOA算法優(yōu)化模型參數(shù)；最后通過對測試數(shù)據(jù)的預(yù)測結(jié)果進行疊加綜合，得到實際的預(yù)測結(jié)果。本文組合模型的算法流程如圖2所示，具體步驟可以總結(jié)為：

1)將建筑物變形時間序列劃分為訓(xùn)練集和測試集；初始化模型參數(shù)：FrFT階次p=0.1,…,0.9，SVM懲罰因子c及核參數(shù)γ的取值區(qū)間，果蠅種群數(shù)量N和最大迭代次數(shù)T；

2)在離線模型訓(xùn)練階段，利用FrFT對時間序列進行分解，并結(jié)合RVM特征選擇獲取最優(yōu)階次對應(yīng)的子序列，利用IFOA選取各子序列的最優(yōu)參數(shù)，訓(xùn)練SVM模型；

3)在在線迭代預(yù)測階段，利用FrFT方法和步驟2)得到的最優(yōu)階次，獲得K個最優(yōu)子序列，利用訓(xùn)練階段獲得的最優(yōu)IFOA-SVM回歸模型，對每個子序列進行預(yù)測，最后根據(jù)式(19)對各子序列預(yù)測值進行綜合累加，得到真實的建筑物變形預(yù)測值。

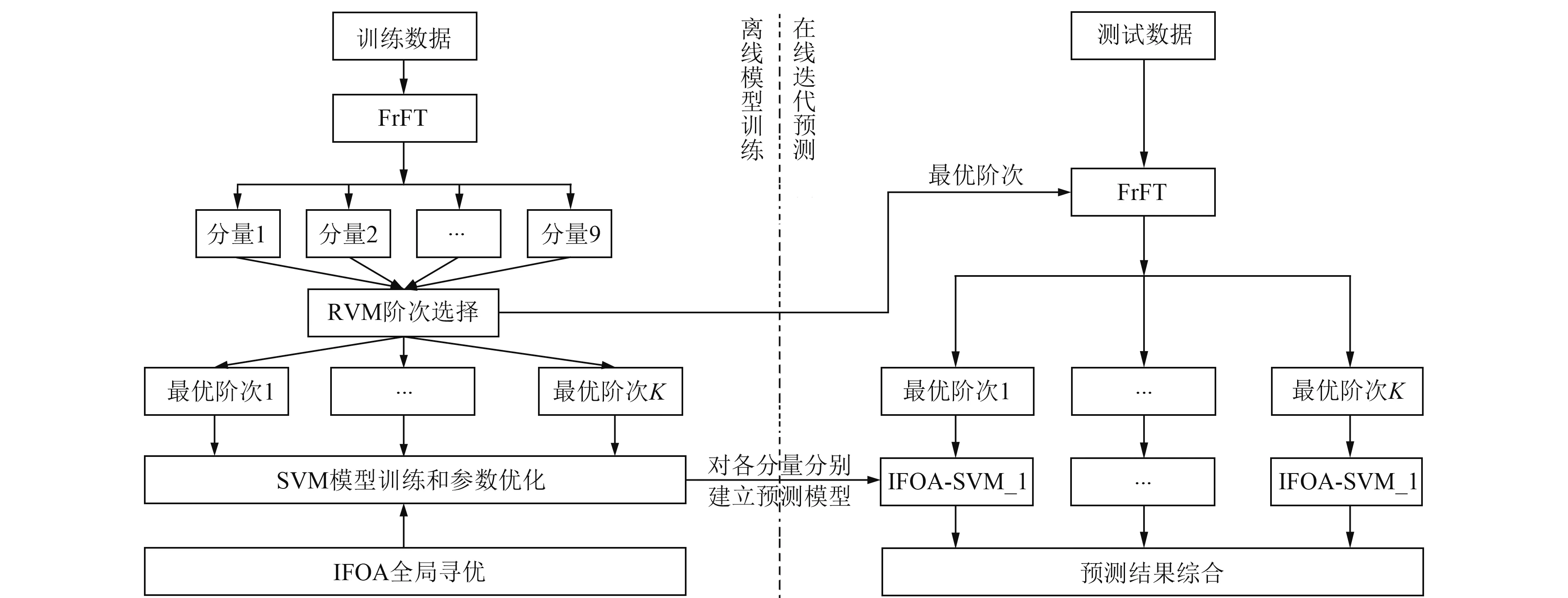
圖2 組合預(yù)測模型流程Fig.2 Flow chart of combined forecasting model

2 實驗及結(jié)果分析

2.1 實驗數(shù)據(jù)及模型評估指標(biāo)

為驗證本文組合預(yù)測模型在實際使用過程中的預(yù)測性能，選用我國西南地區(qū)某混凝土大壩2003-01～2005-02期間水平位移數(shù)據(jù)開展實驗，采樣檢測1月/期。該大壩總共布設(shè)6個水平位移監(jiān)測點，經(jīng)過數(shù)據(jù)分析發(fā)現(xiàn)各監(jiān)測點的水平位移變化規(guī)律大致相同，因此本文選擇具有代表性的3號監(jiān)測點記錄的數(shù)據(jù)進行分析(圖3)。可以看出，在前5期和第8～15期觀測周期內(nèi)，大壩位移變化較為平緩，其余時間變化較大，呈現(xiàn)出典型的非線性、非平穩(wěn)和波動性特征。

圖3 大壩變形原始時間序列Fig.3 Original time series of dam deformation

為定量評估本文組合模型的變形預(yù)測精度，采用預(yù)測值與真實值之間的相對誤差(relative error, RE)和均方根誤差(root mean square error, RMSE)作為評估指標(biāo)：

(20)

(21)

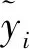
2.2 組合模型預(yù)測結(jié)果

根據(jù)圖2所示流程，首先需要對變形時間序列進行0.1～0.9階次的FrFT分解，并結(jié)合RVM的稀疏性和特征選擇能力實現(xiàn)對最優(yōu)K個FrFT階次的選取。圖4給出利用VBEM算法求解RVM模型，在迭代終止時權(quán)值向量的取值結(jié)果，可以看出，經(jīng)RVM特征選擇后，階次為0.3、0.7和0.8的3個子序列對應(yīng)的權(quán)值較大，其余階次子序列對應(yīng)的權(quán)值均接近于0。圖5給出0.3階、0.7階和0.8階子序列波形，對比圖4和5可以看出，RVM選出的3個子序列都包含了原始序列中的不同維度信息：0.3階子序列波形變化比較劇烈，且數(shù)據(jù)之間的關(guān)聯(lián)性較弱，反映出原始序列中的波動性特性；0.7階子序列呈現(xiàn)出較明顯的上升趨勢，反映原始序列中的趨勢性信息；0.8階子序列表現(xiàn)出一定的周期性，反映原始序列中隱含的周期性信息。上述結(jié)果表明，經(jīng)過FrFT分解后，每個子序列都從不同維度反映了原始序列中的變形信息，對原始序列進行FrFT分解的過程有效弱化了對不同信息進行分析時的相互干擾和相互影響，且每個子序列的波形變化曲線相對于原始曲線更加簡單平滑，降低了后續(xù)預(yù)測模型的復(fù)雜度。

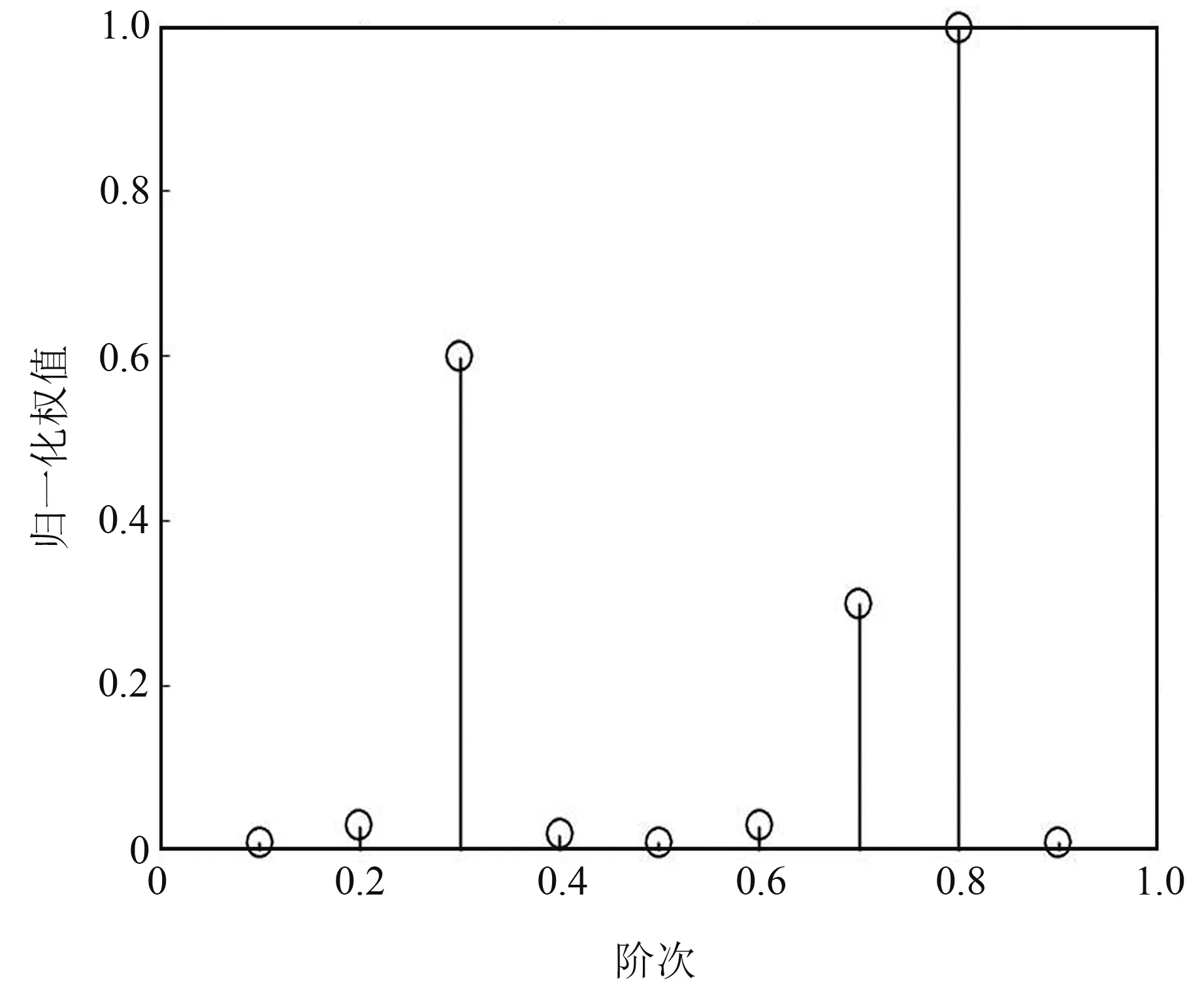
圖4 RVM階次選擇結(jié)果Fig.4 Order selection results of RVM

根據(jù)圖2所示算法流程，在FrFT完成時間序列分解后，利用IFOA-SVM對每個子序列分別進行建模預(yù)測。實驗中，將前12期數(shù)據(jù)作為訓(xùn)練樣本用于IFOA-SVM建模和參數(shù)優(yōu)化，剩余9期數(shù)據(jù)作為測試樣本，得到的預(yù)測結(jié)果如圖6(a)～6(c)所示，圖6(d)給出對每個子序列結(jié)果綜合疊加后得到的最終預(yù)測結(jié)果。

從圖6可以看出，組合模型通過FrFT分解能夠深度挖掘數(shù)據(jù)中隱含的物理規(guī)律信息，使分解后的每個子序列呈現(xiàn)出較為簡單平滑的變化趨勢，從而明顯降低后續(xù)預(yù)測難度，提升預(yù)測性能。根據(jù)式(20)和式(21)可以計算得到預(yù)測結(jié)果的最大RE為1.33%，RMSE為0.072 9。

2.3 與其他預(yù)測方法比較分析

表1給出在相同條件下分別采用組合預(yù)測模型、SVM、GM(1,1)和LSTM四種模型進行預(yù)測得到的結(jié)果和對應(yīng)的預(yù)測殘差。對表1所示結(jié)果進行分析可知，傳統(tǒng)灰色GM(1,1)預(yù)測模型在初期能夠獲得較高的預(yù)測精度，但隨著預(yù)測時間的增長，其預(yù)測性能出現(xiàn)了較大波動，預(yù)測模型的最大RE為8.46%，RMSE為0.634 1；SVM模型的預(yù)測精度要略高于GM(1,1)模型，其預(yù)測結(jié)果的最大RE為3.17%，RMSE為0.343 3；LSTM在進行變形預(yù)測時會加入對前期位移數(shù)據(jù)的回憶，具備動態(tài)預(yù)測能力，因此相對于GM(1,1)模型和SVM模型的預(yù)測性能出現(xiàn)明顯提升，其預(yù)測結(jié)果的最大RE為2.65%，RMSE為0.230 8，能夠滿足實際工程應(yīng)用要求的預(yù)測精度，而本文組合模相對于LSTM模型性能提升超過120%，具有更好的應(yīng)用前景。

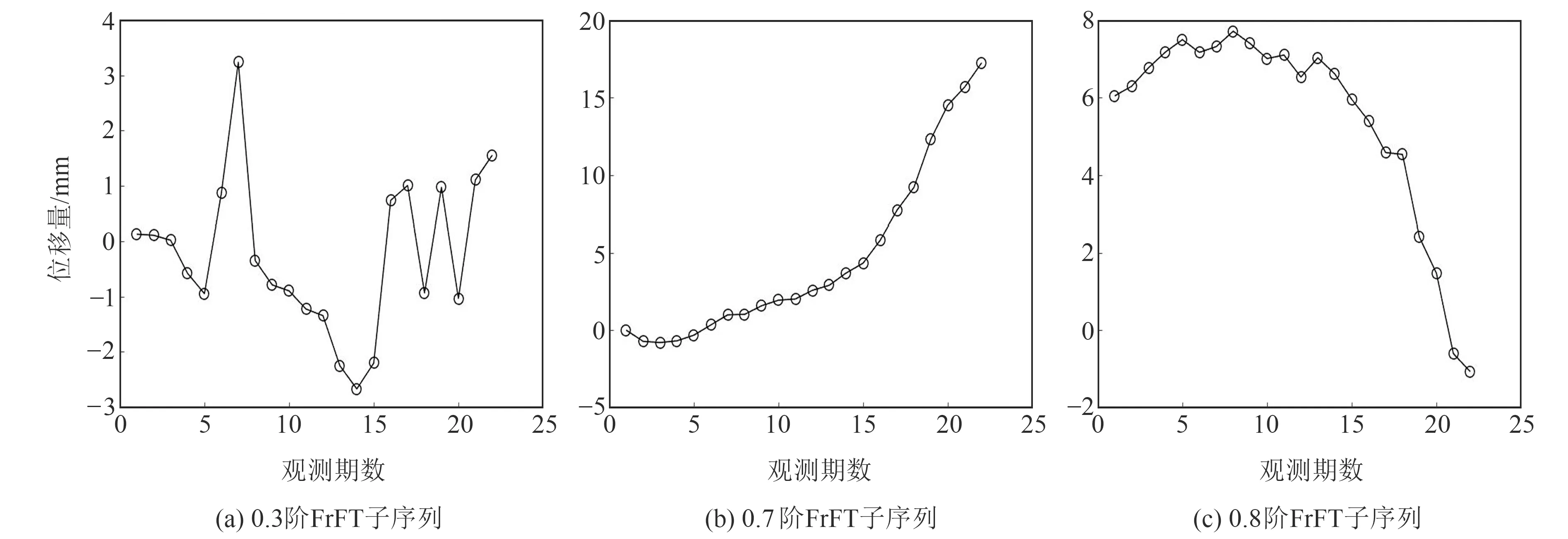
圖5 FrFT分解結(jié)果Fig.5 FrFT decomposition results

圖6 組合模型預(yù)測結(jié)果Fig.6 Predictionresults of the combined model

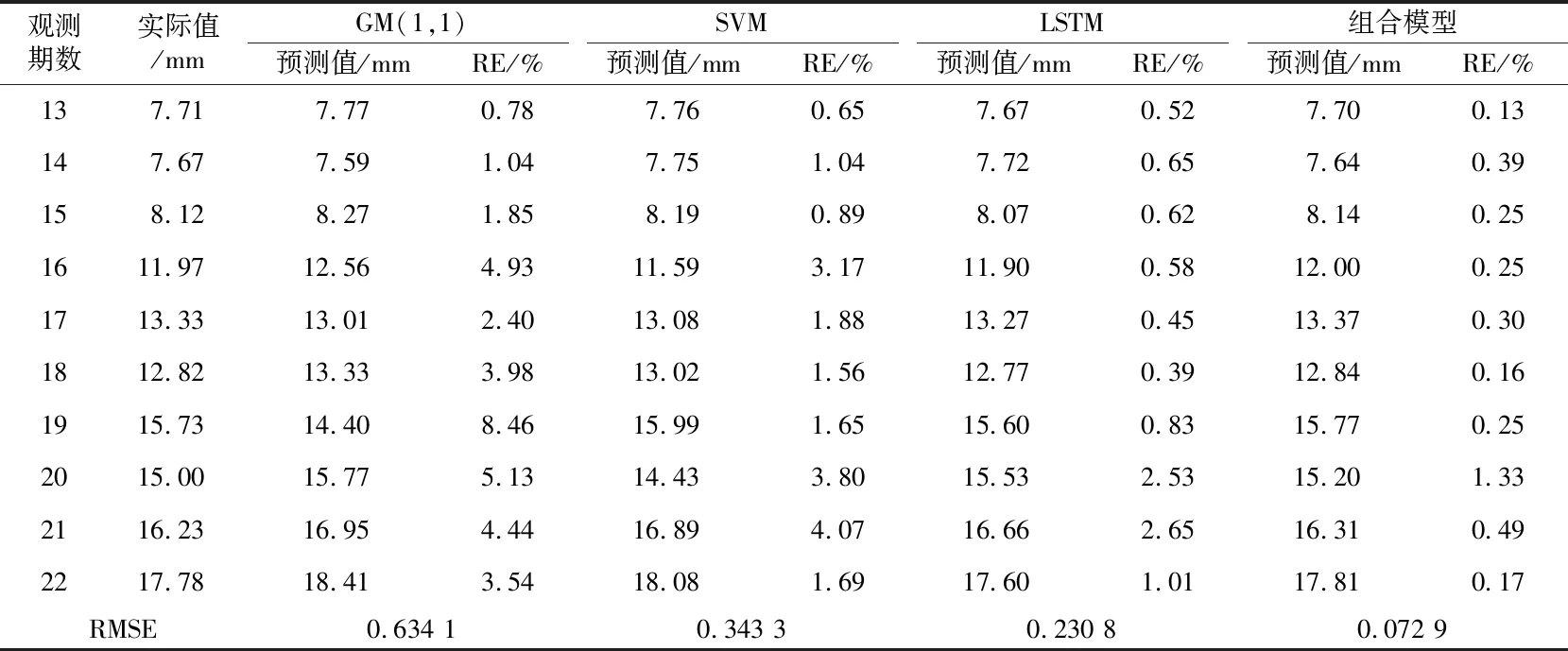
表1 不同方法的預(yù)測結(jié)果

3 結(jié) 語

建筑物變形數(shù)據(jù)是一種典型的非線性、非平穩(wěn)和波動性時間序列，傳統(tǒng)基于單一模型的預(yù)測方法由于無法充分挖掘數(shù)據(jù)中的隱含信息，存在預(yù)測精度低、噪聲穩(wěn)健性差的問題。本文基于分解-預(yù)測-重構(gòu)的思路，利用FrFT結(jié)合RVM將復(fù)雜變形數(shù)據(jù)分解為K個結(jié)構(gòu)簡單子序列，進而利用IFOA-SVM對每個子序列進行建模預(yù)測，通過疊加綜合獲得最終預(yù)測結(jié)果。實驗結(jié)果表明，組合預(yù)測方法能夠獲得更高的預(yù)測精度和噪聲穩(wěn)健性，相對于單一模型具有更為廣闊的應(yīng)用前景。