基于特征提取和譜匹配優化的區域地震動時程構建方法

胡進軍，王中偉，張 輝，靳超越，胡 磊

(中國地震局工程力學研究所地震局地震工程與工程振動重點實驗室，黑龍江，哈爾濱 150080)

在結構抗震設計中，重要建筑和不規則建筑通常需要通過動力時程分析得到結構的非線性反應特性，選擇不同的地震動作為結構非線性動力分析的輸入荷載會得到不同的結果，而地震動輸入結構前通常需要調整其反應譜與設計反應譜一致[1]，因此，如何獲得合理、真實且匹配目標反應譜的地震動時程，是減少結構響應不確定性的重要問題。目前相關地震動模擬方法主要有三角級數法[2?4]、經驗格林函數法[5?6]、隨機有限斷層法[7? 8]和寬頻帶模擬方法[9]等，這些方法通常根據與震源相關的頻域參數合成人工地震動，難以全面考慮區域地震構造背景、地殼介質和場地特征等引起的差異[10?11]。以三角級數法為例，由于受強度包線的控制，該方法生成的地震動時程具有很強的相似性，不能針對不同區域合成考慮區域性差異的地震動。雖然目前考慮場地項合成地震動有傳遞函數法和四分之一波長法[12]，但這要求詳細、準確的區域地質資料。由于目前地震動模擬很難考慮地震發生全過程的所有因素，且合成的地震動缺乏區域性差異，這些方法構造的人工地震動與真實地震動之間有較大的差別，在用于抗震設計或評估時會增大輸入地震動的不確定性。

基于實際強震記錄合成反應譜匹配的地震動主要有頻域和時域方法。頻域方法[13? 15]首先利用一組特定形式的函數分解地震動時程，再通過調整這組函數的幅值使其反應譜與目標反應譜一致，最后根據新的幅值重組得到新地震動時程，重復以上步驟最終實現反應譜匹配的目的。與頻域方法相比，時域方法的匹配精度更高，且合成地震動相較原始地震動具有改變程度小的優點[16]，因此時域上反應譜匹配方法受到了廣泛的研究。KAUL[17]首先提出了時域上反應譜匹配的方法，之后LILHANAND 和TSENG[18]將這種反應譜匹配方法應用于匹配多阻尼反應譜，但是其采用的小波不能保持地震動的非平穩性。ABRAHAMSON[19]借鑒前者的算法提出了新的小波函數，雖然這種調整保留了原始地震動的非平穩性，但未考慮其對速度和位移時程的影響，需要通過基線校正來消除速度和位移時程的漂移。HANCOCK 等[20]通過調整小波函數消除了速度和位移時程的漂移，由于其小波形式中包含了基線校正，導致其無法得到解析解，并影響計算速度和效率。AL ATIK和ABRAHAMSON[16]提出了一種不產生速度和位移時程漂移的調整小波函數，從而使反應譜匹配過程中能夠得到小波系數的解析解。張郁山和趙鳳新[21]構造了一種增量位移小波函數，通過微分、時移以及線性調幅得到加速度小波函數。ADEKRISTI 等[22]利用Broyden 修正方法來降低反應譜匹配中由于不同小波之間相互影響所產生的非線性問題。HONG 和HUANG[23]每次只匹配單個周期的反應譜值，避免了由多個小波函數引起的非線性問題。ZENGIN 和ABRAHAMSON[24]將反應譜匹配方法應用于匹配瞬時功率譜，并得到能夠同時匹配反應譜和瞬時功率譜的地震動，從而為合成近場脈沖型地震動提供了新方法。雖然這些時域上地震動合成方法的原理基本相同，但是用于調整反應譜的小波函數在改進，解決反應譜匹配中非線性問題的方法也在改進。

目前頻域和時域合成地震動的方法均有缺陷。頻域方法在調整函數幅值時改變了地震動的非平穩特征[16]，且反應譜匹配的收斂性較差。時域方法雖然能保留地震動的頻譜特征，但由于引入反應譜峰值時間不變的假設來簡化小波幅值的求解過程，將非線性問題用線性方程組近似求解，從而忽略了小波的相互作用以及地震動與其反應譜之間復雜的關系，導致這類方法存在迭代效率低、收斂性較差和匹配精度低等問題。此外，由于地震的產生受震源效應、傳播路徑和場地效應的影響[25?26]，且地震動存在隨機不確定性[26]，頻域和時域方法都無法合成出合理考慮區域特征的地震動。

相較于頻域合成的地震動，時域方法合成的地震動的非線性動力反應與實際地震動的結果更為相似[27]，因此，本文基于時域方法合成地震動。為了實現考慮區域特征、降低不確定性且匹配反應譜的目標，本文提出了一套完整且高效的地震動合成新方法。該方法首先基于主成分分析算法得到包含目標區域地震動特征的種子地震動，再基于粒子群算法優化時域上反應譜匹配方法，用此方法調整種子地震動的反應譜，最終得到可模擬目標區域地震的合成地震動。為了驗證該方法的可行性、合理性和有效性，本文基于中國四川地區的地震動數據，給出了該方法的實際應用案例與分析結果。

1 方法

1.1 主成分分析提取種子地震動

主 成 分 分 析[28](Principal components analysis,PCA)是一種降低數據維度的算法，該算法通常用于去除高維數據的噪聲和提取重要特征[29]。高維數據在某一維度上特征的重要程度用數據投影到該維度后的方差衡量，方差越大則數據的特征越重要。PCA 算法將m維數據映射到n維上(m>n)，不僅要讓數據在這n維上對應的方差最大，且這些維度之間相互正交，為此該算法首先找出使數據投影的方差最大的坐標軸，然后從與之前所有坐標軸正交的超平面中找出使數據投影的方差最大的坐標軸，以此類推，最終找出n個坐標軸并完成數據降維。將這一方法應用于地震工程，能從一組地震動數據中得到包含原始數據特征的種子地震動。

主成分分析方法得到種子地震動的具體步驟如下：

1)將m條地震動數據按行組成矩陣X。

2)對矩陣X按行進行零均值化處理。

3)計算矩陣X的協方差矩陣C，并求出矩陣C的特征值與特征向量：

4)將矩陣C的特征值與特征向量按特征值從大到小排列，取前n個特征向量按順序組成矩陣P，則矩陣P右乘矩陣X即可得到新地震動數據—矩陣Y。

5)矩陣Y中有n條種子地震動，種子地震動的主成分貢獻率(Contributing Rate of Principal Component, CRP)越大，其包含的原始數據的區域地震動特征[30](eigenquakes)越明顯，主成分貢獻率的計算公式如下：

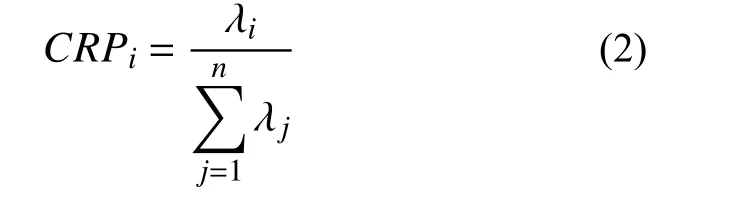
其中，λi為矩陣C的第i個特征值(降序)。

時域上反應譜匹配方法的基本思路是在地震動的加速度時程上添加一組幅值很小的小波，使其反應譜值與目標反應譜值之間的差值減小，通過迭代計算實現反應譜匹配；求解小波幅值是一個非線性問題，為了用線性方程解決該問題，假設在地震動加速度時程上添加小波后，自振周期為Ti的單自由度結構的加速度達到峰值的時間ti不變。

反應譜匹配的方法如下：

1)計算周期為Ti時的反應譜差值，公式如下：

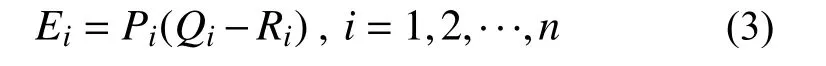
式中：n為周期的個數；Qi為目標反應譜值；Ri為地震動a(t)的反應譜值；Pi由結構加速度峰值確定，當加速度峰值大于零時，Pi=1，否則Pi=?1。

2)在a(t)上疊加小波函數[16]fj(t) 以消除反應譜差值Ej，此時Ri的改變量為cij：

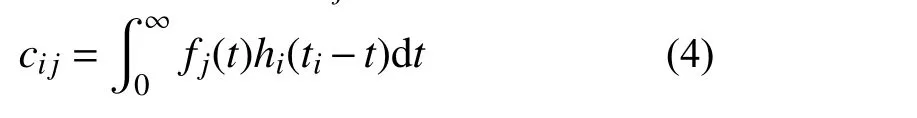
式中：hi(t)為單自由度結構的加速度脈沖響應函數[16]；ti為加速度達到峰值的時間。

3)當周期為Ti時，令添加的所有小波對反應譜值的總改變量等于反應譜差值Ei，則：

1.2 反應譜匹配方法

其中，bj為小波函數fj(t)的幅值。

4)根據式(5)可求解出所有小波的幅值，則新地震動a1(t) 的計算公式如下：

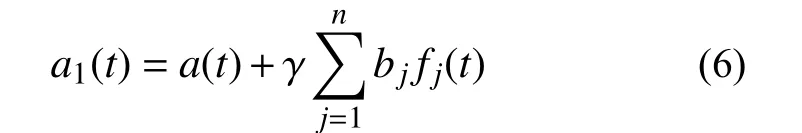
其中，γ 為在0 到1 之間的縮放系數[16]。

用a1(t)代替a(t)，重復以上步驟，直到反應譜之間的差值小于設定差值為止。

1.3 基于粒子群算法的優化原理

目前時域上反應譜匹配方法并沒有對式(6)中γ 的取值做出明確的說明，因此現有方法普遍存在迭代效率低、反應譜匹配精度低的問題。本文采用機器學習中的粒子群算法[31](Particle swarm optimization, PSO)來尋找每次迭代過程中γ 的最優解，由于PSO 算法能夠共享所有粒子的信息來調整粒子在尋優過程中的速度和位置，采用該算法能快速找到問題的最優解，從而提高反應譜匹配方法的迭代效率與匹配精度。

粒子群算法的原理如下：

1)參數設置與種群初始化。

設置相關參數，例如：粒子的數目、搜索范圍和速度范圍以及迭代次數等，根據設置的參數隨機確定粒子的位置和速度。

2)計算極值，確定最優解。

根據定義的適應度函數計算粒子的適應度值，找出每個粒子的個體極值，再從所有個體極值中找出群體極值作為最優解。

3)更新粒子的速度和位置，公式如下：

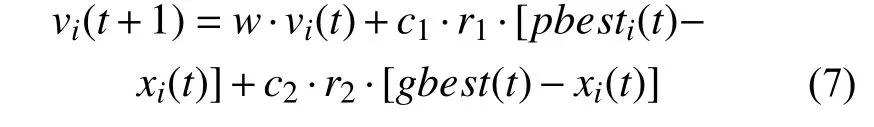
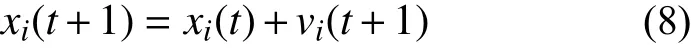
式中：i=1, 2, ···,N，N為選取的粒子總數；t為當前迭代步數；vi為粒子的速度；xi為粒子的當前位置；w為慣性因子(非負)，用于調節算法的尋優能力；r1和r2是0 到1 之間的隨機數且相互獨立；c1、c2是學習因子；pbesti為個體最優解；gbest為全局最優解。

本文的慣性因子采用線性遞減權值策略，公式如下：

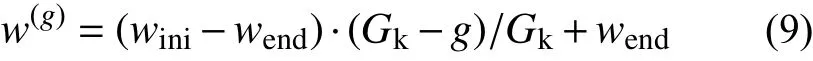
式中：g為迭代次數；w(g)為第g次迭代的慣性因子；Gk為最大迭代次數；wini為初始慣性權值；wend為最終慣性權值。

4)判斷迭代次數與最優解是否符合要求。

當達到最大迭代次數或者最優解滿足設定值時，迭代結束，否則返回步驟2。

在上述原理中，單個粒子的優劣要通過適應度函數來評價。本文構造了四種誤差函數,其中任意一種均可作為適應度函數，從而滿足不同情況下對反應譜匹配精度的要求。四種誤差函數的計算公式如表1 所示。

表1 誤差函數的定義Table 1 Definition of error function

式中：N為選取周期點的個數；Ti為第i個自振周期；Sac(Ti)為周期為Ti時新地震動的反應譜值，Sat(Ti)為周期為Ti時目標反應譜值。

本文應用粒子群算法求反應譜匹配過程中γ 最優解的流程圖如圖1。

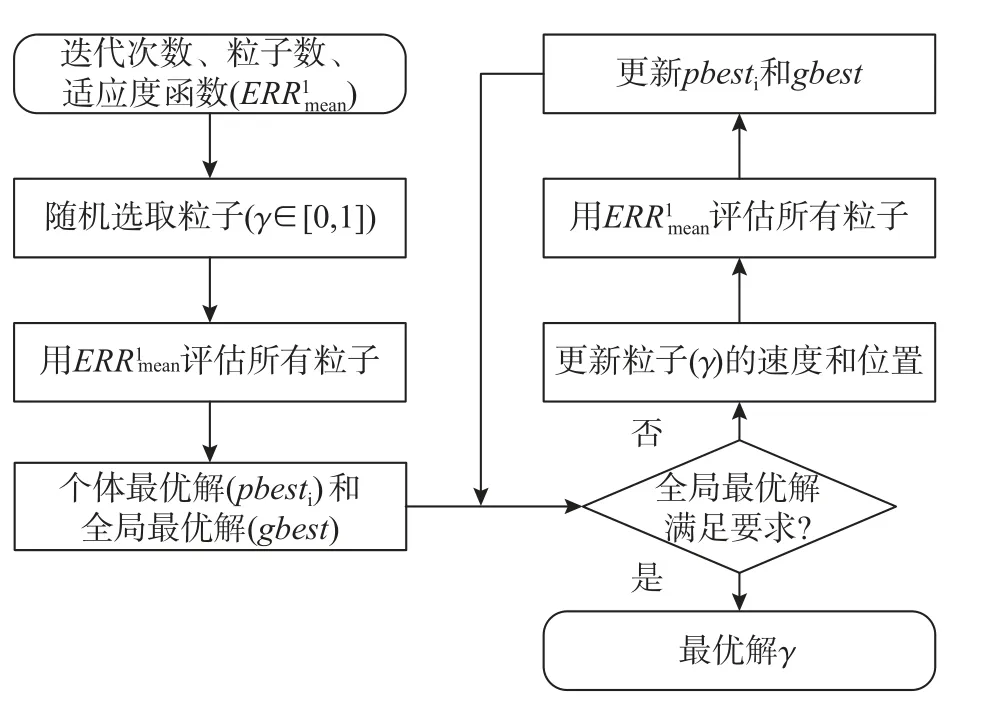
圖1 粒子群算法求最優解γ 的流程圖Fig. 1 Flow chart of particle swarm optimization for solving optimal solution γ

2 地震動合成整體思路

由上述方法可知本文合成地震動的整體思路分為兩步：首先從目標區域選取一組區域地震動，用PCA 算法從中得到包含區域地震動特征的種子地震動；再用基于PSO 算法優化的時域內反應譜匹配方法調整種子地震動，通過疊加小幅值的小波調整其反應譜與目標反應譜一致，最終得到合成地震動。整體流程圖如圖2 所示。

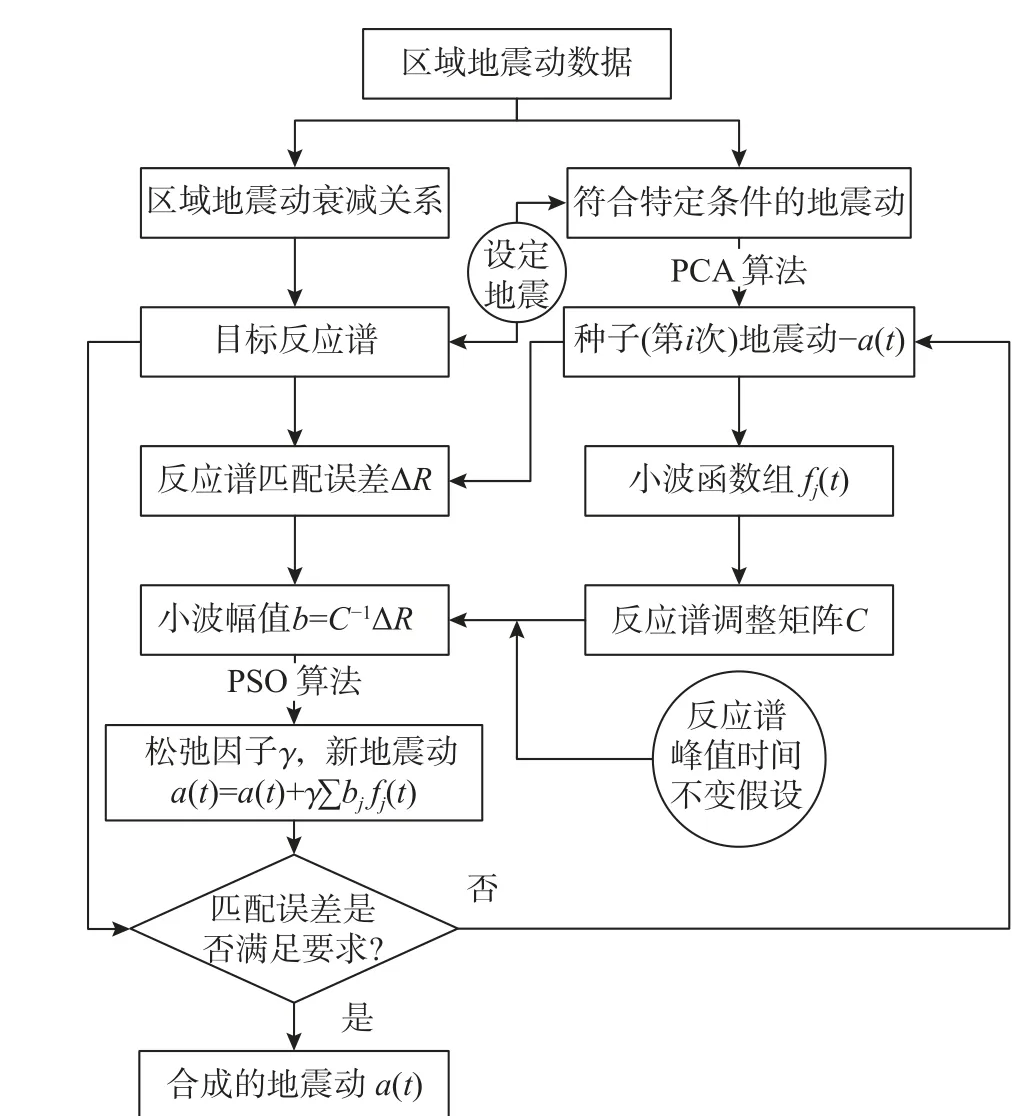
圖2 本文的地震動合成流程圖Fig. 2 The flow chart of ground motion synthesis

PCA 算法得到種子地震動的優點：1)降低了地震動的不確定性，地震動在時域和頻域上的不確定性會導致結構地震響應也具有不確定性[32]，而基于最大方差理論的PCA 算法能從一組地震動中得到不確定性更低的種子地震動；2)具有區域特征，由于PCA 算法能找到一組數據的特征并得到包含此特征的新數據，因此，如果選擇的一組地震動具有區域特征，則種子地震動也具有區域特征。此外，從目標區域的地震動數據庫中挑選地震動應遵循震級、震中距和場地條件等與設定條件基本相符的原則，則用PCA 算法得到的種子地震動也滿足這三個條件的約束。正是由于種子地震動具有上述兩個優點且滿足一定的約束條件，用它來模擬設定地震在目標區域可能產生的地震動是合理的。

由于種子地震動的反應譜一般與設定區域的目標反應譜不匹配，因此，還需要用優化的反應譜匹配方法調整種子地震動的反應譜與目標反應譜一致。由于該方法不會對種子地震動的時域和頻域特征產生較大的改變，因此，最后合成的地震動可用于模擬設定地震在目標區域產生的地震動。

AL ATIK 和ABRAHAMSON[16]提出的反應譜匹配的改進方法為了保證迭代的收斂性，在單次匹配過程中使匹配周期從短周期逐漸擴大到全周期，且迭代過程中未優化縮放系數γ 的取值，因此，該方法的迭代效率和匹配精度相對較低。用PSO 算法優化該方法后，求解γ 的最優值能提高迭代的收斂性，同時，全周期匹配也避免了多次疊加小波降低匹配精度的問題，因此，本文的優化方法提高了迭代的收斂性、效率和匹配精度。

3 方法的驗證

為了驗證本文提出的基于實際記錄的地震動時域合成方法的可行性，以四川地區的地震動為基礎進行目標區域的地震動構建。本文的反應譜匹配方法僅考慮單一阻尼，下文算例中所有反應譜對應的阻尼比均為5%。

3.1 基于PCA 方法獲取種子地震動

假定需要合成目標區域為四川地區、震級5 級、震中距30 km、場地條件為土層的地震動，為了體現區域地震動特征，選取34 條四川雅安余震的地震動記錄，以此合成雅安地區的種子地震動，這些地震動記錄的震級為4.5～5.4、震中距為25 km～35 km，詳細的地震信息如表2 所示。

表2 區域地震動信息Table 2 Regional ground motion information

通過PCA 算法的分析計算，可依據主成分貢獻率從大到小選取對應的種子地震動，本文選取對應CRP最大的4 條地震動作為種子地震動，依次將其記為地震動1～4，其加速度時程圖如圖3 所示。

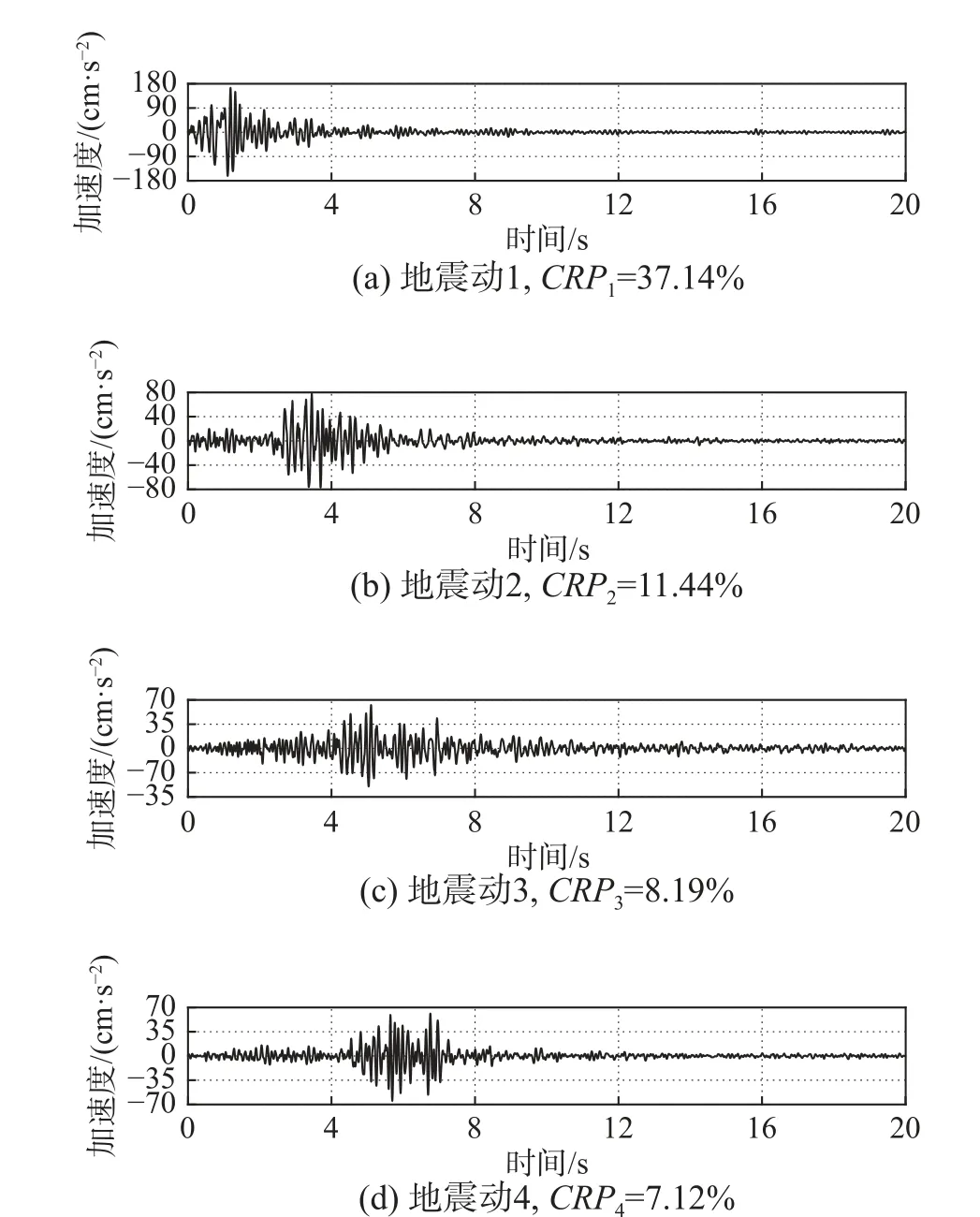
圖3 種子地震動的加速度時程Fig. 3 The acceleration time history of the seed ground motion

3.2 優化反應譜匹配方法合成地震動

為了使目標反應譜具有四川地區的地震特性，本文選擇了基于實際數據得到的川滇地區地震動預測模型[33]，根據設定的震級和震中距即可得到目標反應譜(控制周期點見參考文獻[33]，不含PGA)。如圖4 所示，灰色曲線是目標反應譜，其他曲線是4 條種子地震動的反應譜。

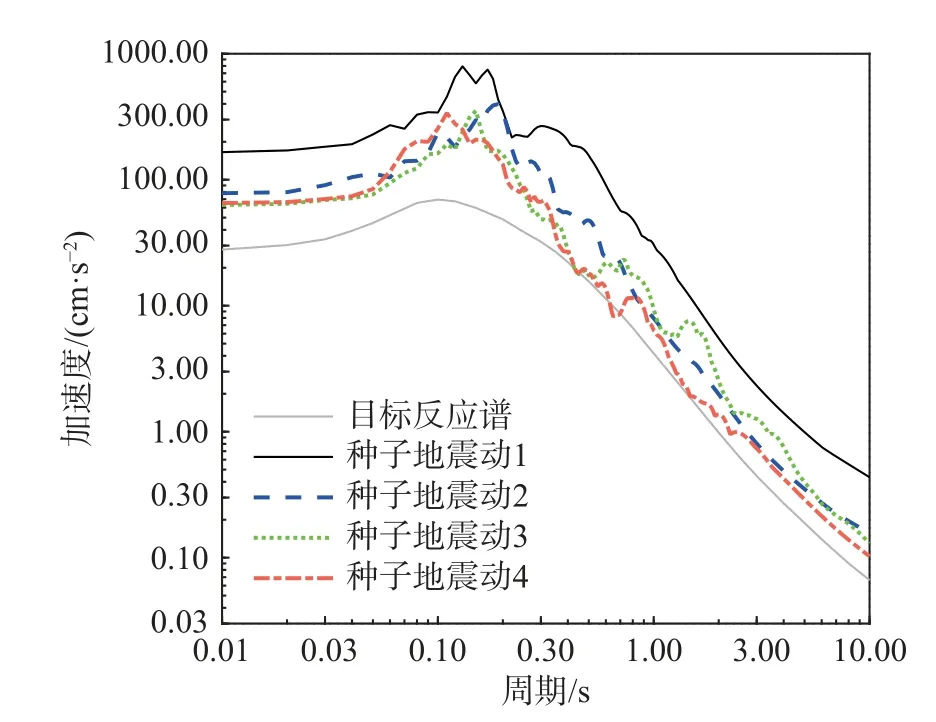
圖4 種子地震動反應譜與目標反應譜Fig. 4 Seed ground motion response spectrum and target response spectrum

為了保證收斂性，種子地震動需要適當的調幅和補零[16]。由于迭代效率的提高，本文設置迭代次數為20 次即可使反應譜差值降到很低的水平，實際應用中也可以預設合適的匹配精度。為了找出γ 的最優解，PSO 算法的粒子數和迭代次數不宜過低，本文設定粒子數為20 個、迭代次數為5 次。為了使合成地震動的反應譜與目標譜之間的差值更小，本文選擇反應譜匹配差值的總體平均值(ERR1mean)作為粒子群算法的適應度函數。由種子地震動調整得到的4 條合成地震動的加速度時程如圖5 所示。

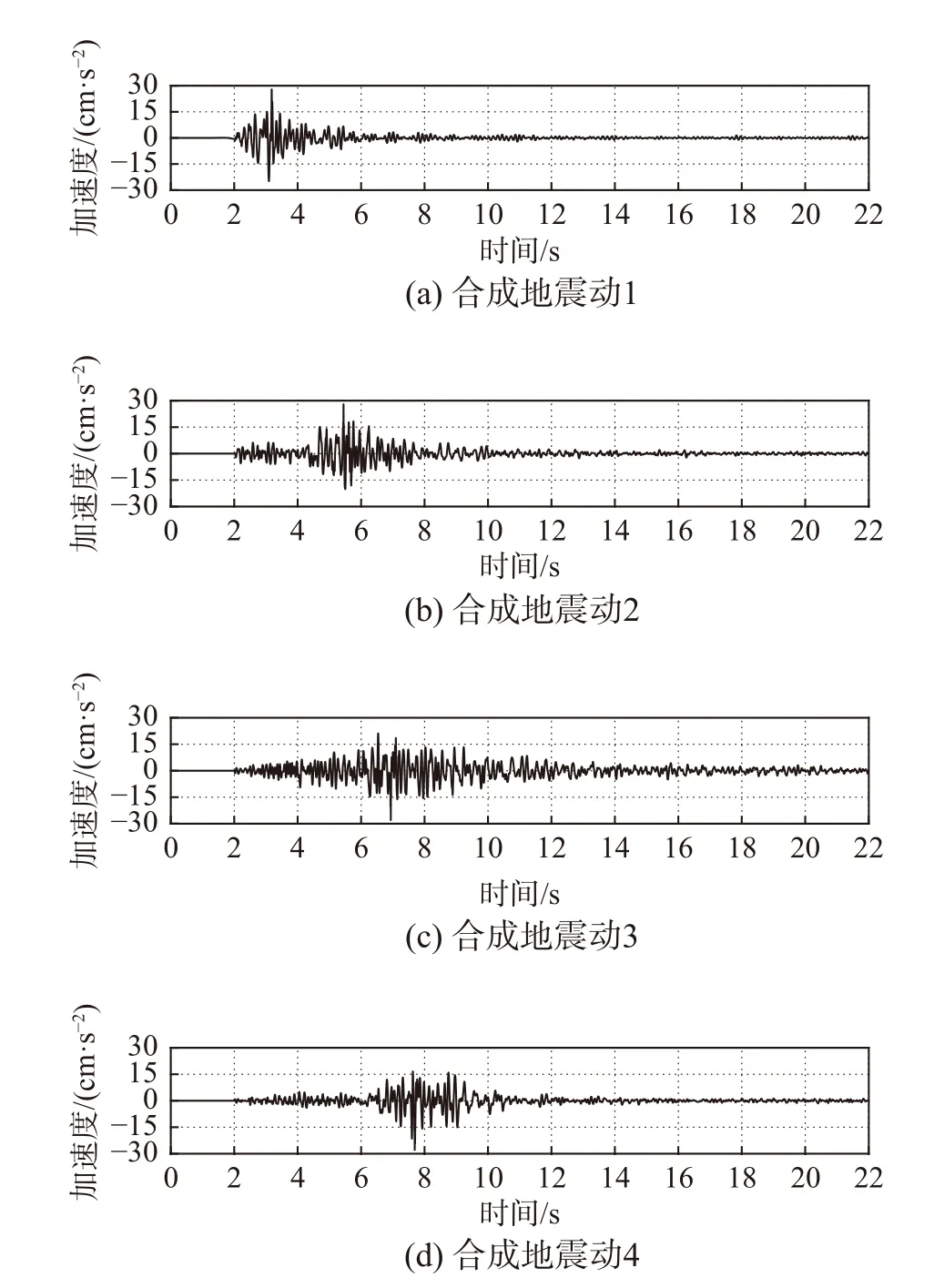
圖5 合成地震動的加速度時程Fig. 5 The acceleration history of the synthetic ground motion

圖7 是4 條合成地震動在控制周期點上ERR1和ERR2的曲線圖，可以看出在所有周期上ERR1不超過0.045 cm/s2，ERR2不超過0.3%，因此優化的反應譜匹配方法能得到匹配精度很高的合成地震動，至此合成地震動方法的可行性得到了驗證。

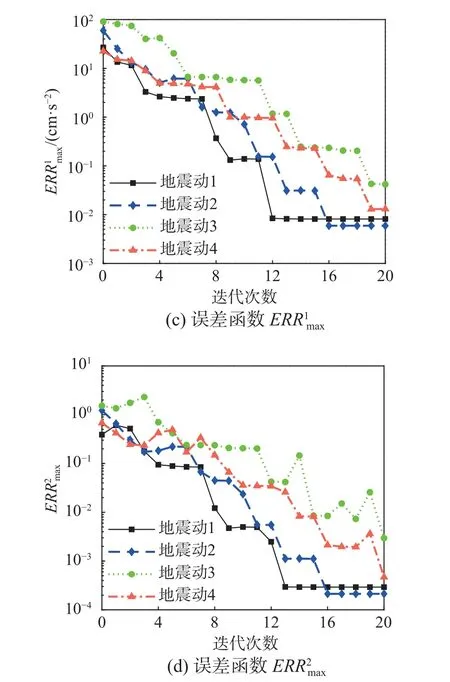
圖6 匹配誤差隨迭代次數增加的變化曲線Fig. 6 The variation curve of matching error with the increase of iteration number

3.3 合成地震動的結果分析

從圖7 可以看出，合成地震動的反應譜與目標譜基本一致，但在匹配反應譜時種子地震動的時程需要調幅和疊加小波函數，因此要從時域和頻域上分析此過程是否改變了地震動的區域特征。由于種子地震動調幅為初始地震動的過程不會改變區域特征，且小波函數均疊加在初始地震動上，因此分析比較初始地震動與合成地震動即可確定后者是否仍具有區域特征，為此選擇種子地震動1 對應的初始地震動和合成地震動為本節的分析對象。

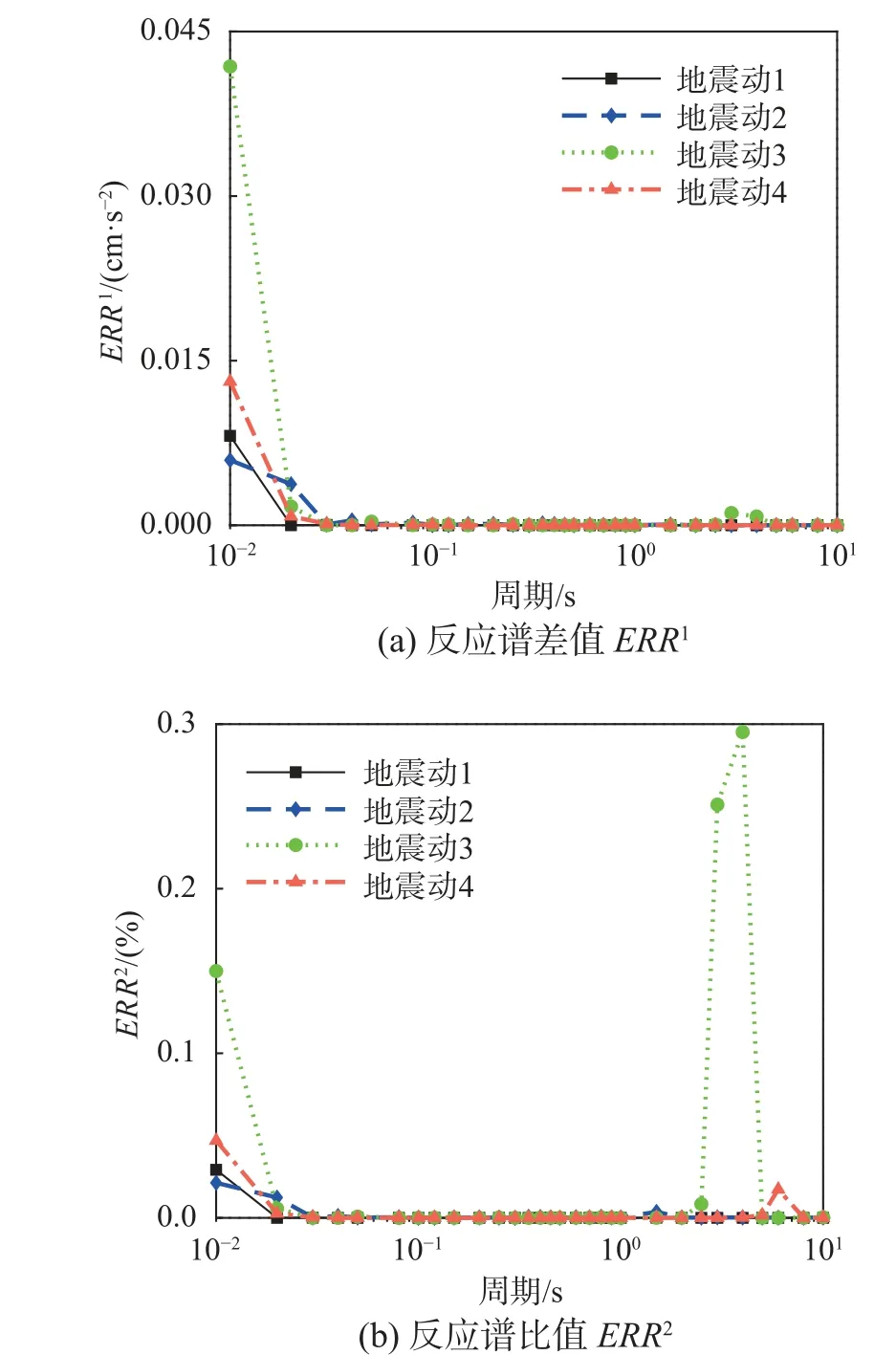
圖7 合成地震動的匹配誤差Fig. 7 Matching error of the synthetic ground motion

如圖8 所示，初始地震動和合成地震動的加速度和速度時程非常相似，兩者的位移時程基本相同，且最大位移相差不大；從圖9 可以看出初始地震動和合成地震動的歸一化Arias 強度曲線基本一致，且兩者的顯著持時D70和D90相差不超過0.024 s，故兩者的能量分布是一致的，因此這兩條地震動在時域上的特征基本沒有差別。

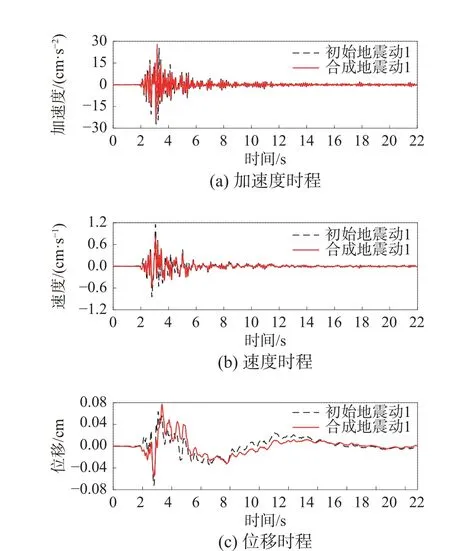
圖8 初始地震動和合成地震動的時程Fig. 8 Time history of initial and synthetic ground motion

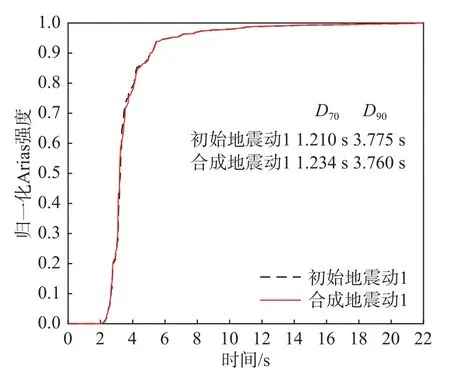
圖9 初始地震動和合成地震動的歸一化Arias 強度Fig. 9 Normalized Arias intensities for initial and synthetic ground motion

如圖10 所示，兩條地震動的傅里葉幅值譜基本一致。由于地震動是非平穩信號，因此還需要用短時傅里葉變換分析地震動的時頻特征。圖11分別是兩條地震動的時頻圖，與圖11(a)相比，圖11(b)在2 s～5 s 處存在2 Hz～8 Hz 的低頻成分減少、在3 s 附近存在大于10 Hz 的高頻成分增加的現象，這是由于種子地震動在不同周期下達到加速度峰值的時間ti基本在2 s～5 s，使得疊加小波后這一段時程的改變較大，但從整體上可以看出兩條地震動的時頻特征基本相同，因此兩者在頻域上的特征基本沒有差別。

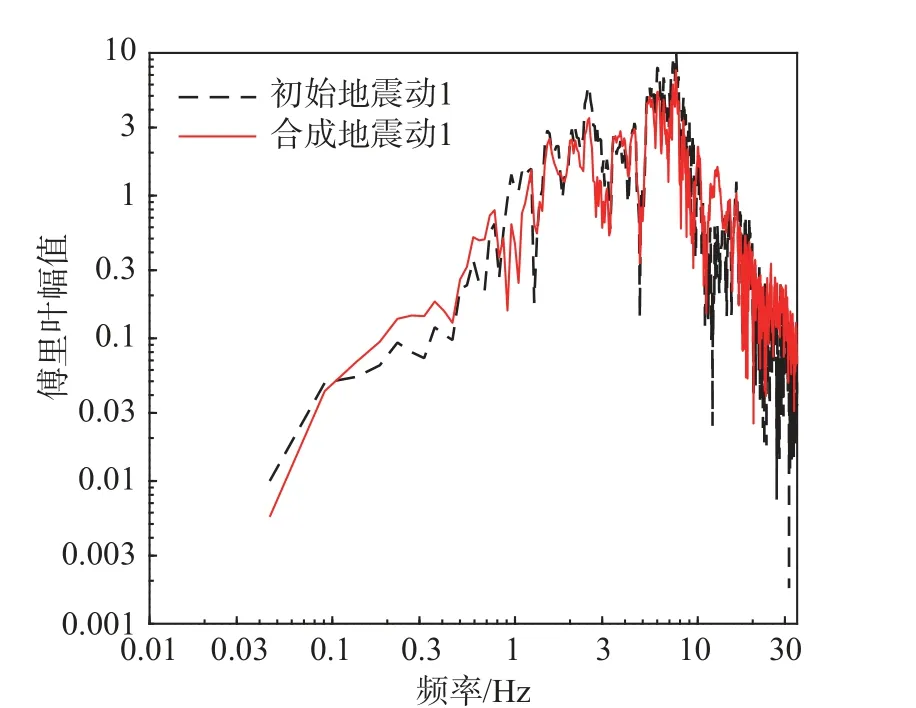
圖10 初始地震動和合成地震動的傅里葉幅值譜Fig. 10 Fourier amplitude spectra of initial and synthetic ground motion

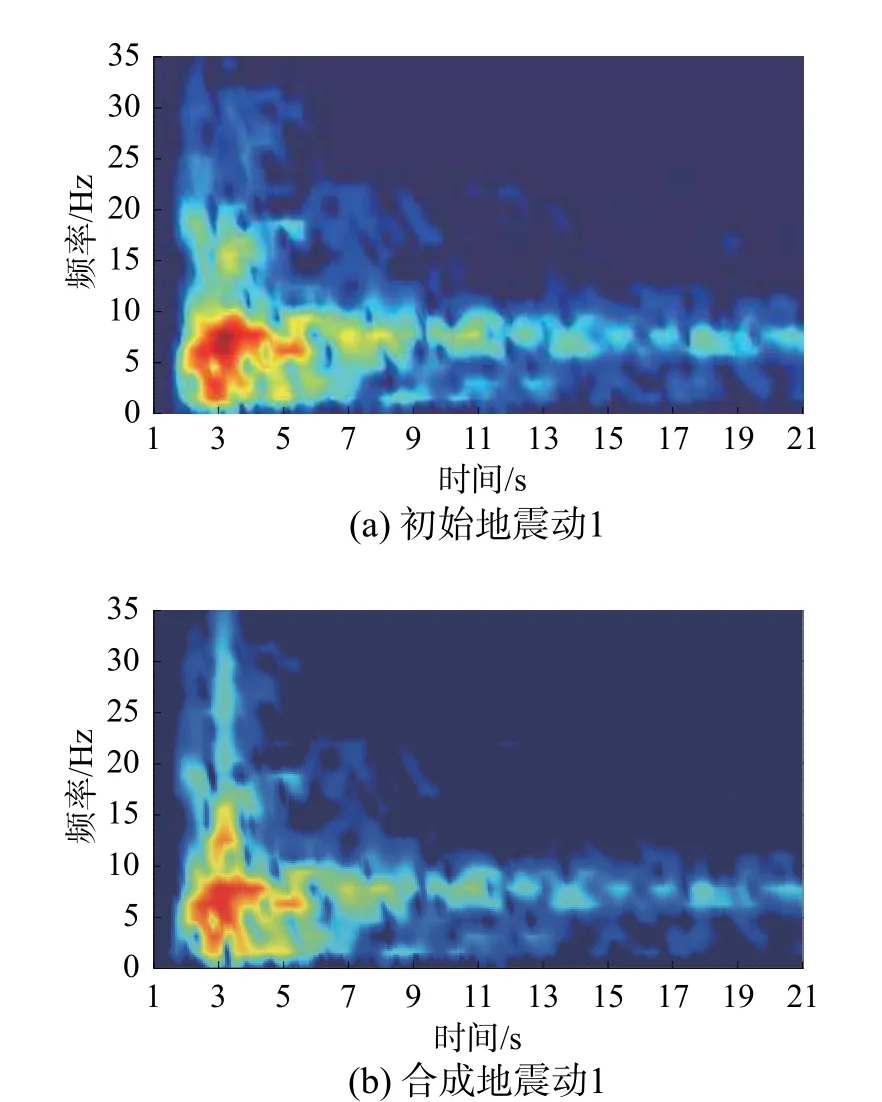
圖11 初始地震動和合成地震動的時頻圖Fig. 11 Time-frequency diagrams of initial and synthetic ground motion

本節從時域和頻域上對合成地震動和初始地震動進行比較，得出兩者的相關特征基本相同的結論，而初始地震動保留了種子地震動中的區域特征，因此合成地震動也具有設定區域的地震動特征，同時其反應譜與目標譜一致，所以用本文合成方法得到的地震動模擬目標區域可能產生的地震是合理的。

4 結論與討論

本文基于實際地震動記錄并結合機器學習算法得到具有區域特征且與目標譜一致的合成地震動，本文的主要結論如下：

(1)提出了一種時域上合成地震動的方法，該方法先由PCA 算法獲得包含目標區域地震動特征的種子地震動，再根據PSO 算法優化的反應譜匹配方法調整種子地震動，使其反應譜與目標譜一致，最終得到可用于模擬目標區域地震的地震動。

(2)與現有的方法相比，用PCA 算法降維處理地震動數據時不僅降低了地震動的不確定性，同時保留了地震動的區域特征，因此相對于選擇實際地震動記錄或是人工地震動，用種子地震動模擬目標區域地震更為合理。

(3)用PSO 算法對目前已有的時域上反應譜匹配方法優化，從而在每次反應譜匹配過程中獲取用于約束小波函數的最優縮放系數γ，此方法大幅提高了反應譜匹配過程中的迭代效率和匹配精度，并使地震動高精度匹配目標譜成為可能。

由于獲取實際地震動特征需要目標區域實際地震動記錄，對于強震數據不豐富的地區可從地震地質背景相似地區的地震動記錄中提取種子地震動。本文考慮區域實際地震動特征的構建方法為解決面向區域的地震動場構建提供了參考。