基于空間特性的臺風風災害評估

任賀賀，柯世堂，楊 杰

(南京航空航天大學土木與機場工程系，南京 210016)

隨著氣候變化，臺風發生頻次和致災程度均呈增強趨勢[1?3]，沿海和海上基礎設施受到不同程度破壞[4?8]。臺風造成的結構破壞程度最初是由風速相關變量表征，1 min 或10 min 最大持續風速[9]、陣風風速[10]等。但是，研究表明，使用單一與強度相關的變量往往不能準確表征臺風破壞潛力[11?14]。

MAHENDRAN[11]首先指出臺風破壞指標應該基于除最大持續風速之外的變量進行表征，并指出具體需要考慮臺風最大風速半徑、移動速度、中心氣壓等。已有研究除最大持續風速之外，其他臺風災害指標包括累計臺風能量[15]、臺風外圍和內圈強度[16?17]、湍動能耗散[18]和能量[2]等。現階段，考慮單因素衡量臺風破壞潛力仍占主導地位。

2005 年全球發生了多次災難性臺風事件，尤其是針對臺風Katrina, Saffir-Simpson(SS)風力等級在描述風災害破壞潛力方面表現出明顯缺陷。學者進一步研究得出，現有考量臺風破壞的指標不能夠準確表征風災害程度。按照SS 風力等級，在同一登陸點，臺風Katrina 登陸時強度等級為3 級，而臺風Camille 登陸時強度等級為5 級，但是臺風Katrina 破壞程度遠大于臺風Camille[13]；同樣的情況發生在2011 年臺風Irene 和2012 年臺風Isaac 與Sandy 之間[19]。這引發了臺風風災害研究由單因素向多因素考慮的轉變。

KANTHA[12]率先開展了非單因素表征風災害程度的探討，其考慮了臺風尺寸并提出臺風危害指數。POWELL 和REINHOLD[13]指出，需要同時考慮臺風強度和尺寸特征，將單位體積內10 m高度處動能在整個臺風區域范圍內進行積分，提出積分動能指標作為臺風破壞力表征。該方法被美國國家颶風研究中心(NHC)實時颶風分析系統采用[20]。后續相關學者也基于此方法開展了諸如積分動能方法在實際預報應用中置信度[21]、隨時間發展歷程積分動能過程[19]等相關研究。IRISH 和RESIO[14]考慮臺風強度和尺寸的同時，進一步考慮風暴前進方向和角度。ZHAI 和JIANG[22]指出使用最大風速和臺風尺寸來表征在美國海岸登陸臺風造成的經濟損失要好于單獨使用二者之一。BAKKENSEN 和MENDELSOHN[23]通過近50 年全球臺風災害數據指出，作為指標參數，最小中心氣壓要優于最大風速。與之類似，KLOTZBACH等[24]研究指出，最小中心氣壓是比最大風速能夠更精確測量的物理量，認為其是評估臺風對結構潛在損害的理想變量。PILKINGTON 和MAHMOUD[25]采用多輸入(最大風速、最小中心氣壓、降水等)人工神經網絡模型預測臺風對經濟的影響。WALKER 等[26]提出Kuykendall 等級，該等級將臺風產生的風暴潮高度和速度通過三維循環模型進行建模，并與多種不同損失方法建立聯系。盡管所有這些研究中建議的變量都有特定應用，但其中一些變量不能準確表征臺風整體風災害，亦或很難在實際工程中應用。具體舉例：KANTHA[12]提出的臺風危害指數，雖是連續量，但其是無界的，且該指標未包含小于臺風強度的風速；POWELL和REINHOLD[13]提出的積分動能表征，對于尺寸小但強度大和尺寸大但強度小的臺風仍具有挑戰，而且實際臺風中不易獲得三維空間風場資料。

筆者前期研究也發現，單獨依據最大持續風速作為臺風風災害評估指標有一定的誤導性[27]，提出基于臺風10 m 高度平均持續風速與結構災害損失百分比函數關系式，作為新的臺風風災害評估指標。在此基礎上，本文針對臺風風災害破壞潛力科學問題，綜合考慮臺風空間特性和強度進行研究。這里需要說明的是，臺風災害涉及風、風暴潮、降雨、洪水和波浪等[28]，本文僅限于結構風災害部分。

1 數值模擬方法及算例

基于可能生成臺風的海表溫度范圍，本文開展4 種不同海表溫度(sea surface temperature, SST)工況臺風模擬研究，分別為26℃、27℃、28℃和29℃，即SST-26、SST-27、SST-28 和SST-29。臺風數值模擬采用WRF-LES 方法[29]，進行6 層雙向嵌套模擬。為了分析不同嵌套層模擬結果的差異性，本文還對各外層區域進行了無嵌套模擬；因此，不同嵌套層結果相互獨立。各嵌套層區域具體為D01、D02、D03、D04、D05 和D06，最外層區域D01 水平網格尺度為15 km，以1∶3 比例向內層嵌套，最內層區域D06 水平網格尺度約為62 m；各嵌套層豎向網格數均為87 層，具體見圖1。D01～D03 采用行星邊界層方案，這是因為水平網格尺度遠大于豎向網格尺度，動量通量的水平成分和豎向成分應分開考慮；D04～D06 采用三維大渦模擬方案，此時水平網格尺度與豎向網格尺度相當，湍流具有三維各向同性特性。具體模擬參數設置如表1 所示。

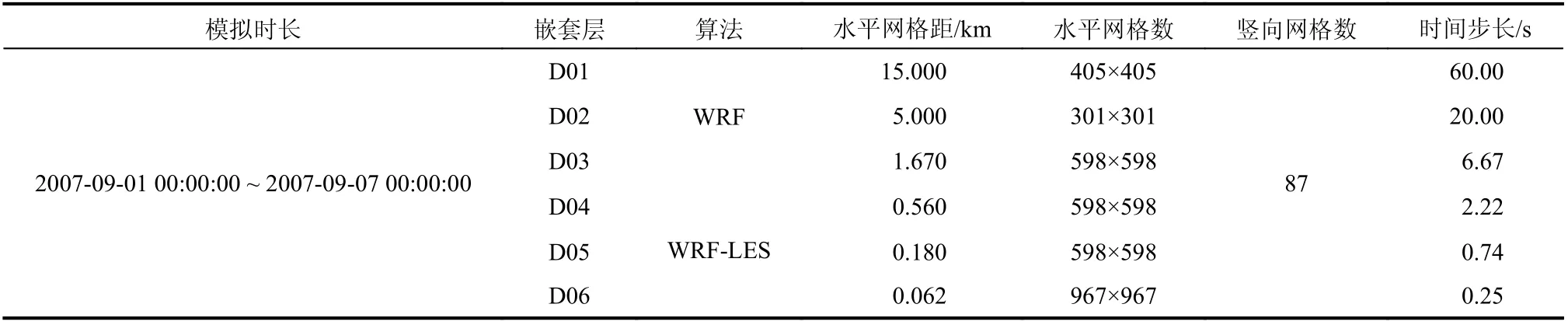
表1 WRF 數值模擬參數設置Table 1 WRF numerical simulation parameter setting

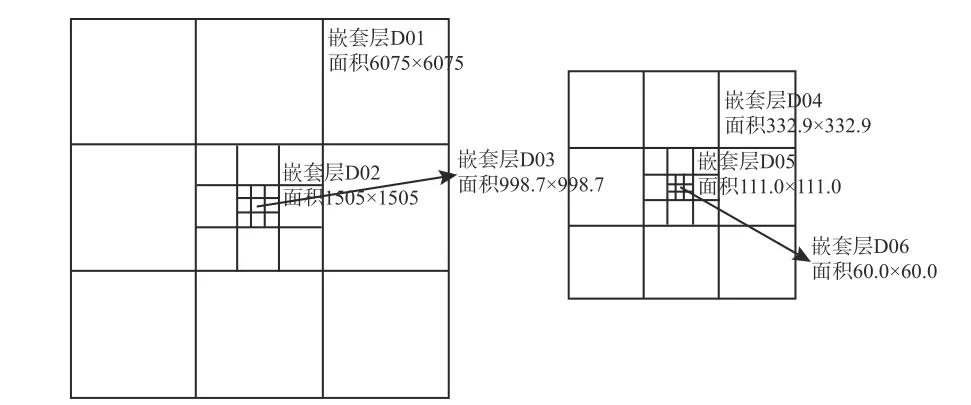
圖1 各嵌套層劃分示意圖及區域面積 /kmFig. 1 Each nesting domain schematic diagram and area

WRF-LES 模擬基本物理參數化方案設置為：行星邊界層方案采用YSU 方案[30]；微物理方案采用WSM6 方案[31]；表層參數化方案為修正的MM5 Monin-Obukhov 方案[32]；模型中熱力學狀態通過在熱力學方程中加入一項時間常數松弛項來維持；同時，大氣長波、短波輻射也利用松弛項進行表征[27,33]。另外，Donelan 摩擦阻力方法與恒定焓粗糙度長度之和被用來表示海氣熱交換和動量交換[34]。需要注意的是，本文研究以方法為主要創新點，具體到陸上或者不同海陸比情況該方法均適用，但是陸上情況會更復雜些[35?37]，將開展進一步研究。

模擬初始速度場為熱帶風暴型軸對稱渦旋，模型最低層最大風速為15 m/s，最大風速半徑為82.5 km，零風速半徑為412.5 km[38]。假定科里奧利參數在整個計算域內均勻分布，選取緯度為20°，對應Coriolis 系數為5×10?5s?1。

2 風災害評估指標因子

根據不同沿海地域建筑結構抗風等級和地區發展程度，前期研究中基于平均持續風速與結構災害損失百分比之間函數關系提出了3 種不同風災害評估指標因子[27]。

2.1 風災害指標因子公式

適用于不同抗風等級結構風災害分析的三種風災害評估指標因子公式具體如下：

式中：D為結構災害損失百分比；U為10 m 高度平均持續風速。

式(1)～式(3)的物理意義可以理解為：分別對應發達、欠發達、發展中沿海地區建筑結構，亦或是分別對應抗風等級高、低、中的建筑結構。其中，三個公式在風速達到60 m/s 時，結構災害損失百分比均達到100%；區別在于，結構災害損失百分比為1%時，風速分別對應40 m/s、20 m/s和30 m/s。本文首先研究不同水平網格精度、不同海表溫度對該風災害評估指標因子的影響；然后基于風災害指標因子，結合考慮臺風空間特性，探究如何更好表征臺風對結構產生的風災害科學問題。

2.2 災害評估指標因子影響因素

從式(1)～式(3)中可以看出，災害評估指標因子與10 m 高度平均持續風速有關。因此，影響10 m高度處平均持續風速的因素，即為災害評估指標因子影響因素。本小節通過不同網格精度和不同海表溫度兩方面分析10 m 高度平均持續風速變化，揭示災害評估指標因子變化規律特征。

2.2.1 不同網格精度對臺風風災害評估指標因子影響

10 m 高度處最大平均持續風速隨不同水平計算網格精度變化規律如圖2 所示。需要指出，不同算例不同嵌套層不同時刻最大平均風速所在位置不同，但均位于臺風眼壁區范圍。此外，因計算資源需求較大，本文首先開展D01～D03 嵌套層模擬，當D03 達到穩態后，再依次開啟D04、D05 和D06 嵌套層模擬。圖2 為D03 達到穩態至模擬結束時各嵌套層10 m 高度處最大平均持續風速隨時間變化過程。D03 (1.67 km)最大平均持續風速明顯小于D04 (555 m)、D05 (185 m)和D06(62 m)，說明千米量級以下網格計算的必要性。對于SST-26，平均風速在D05 和D06 區域趨于一致；其余三個算例，在D04、D05 和D06 區域趨于一致；驗證了本文模擬的網格無關性。上述分析表明，該評估指標因子采用水平計算網格尺度為185 m甚至555 m 時模擬結果即可表征臺風風災害。

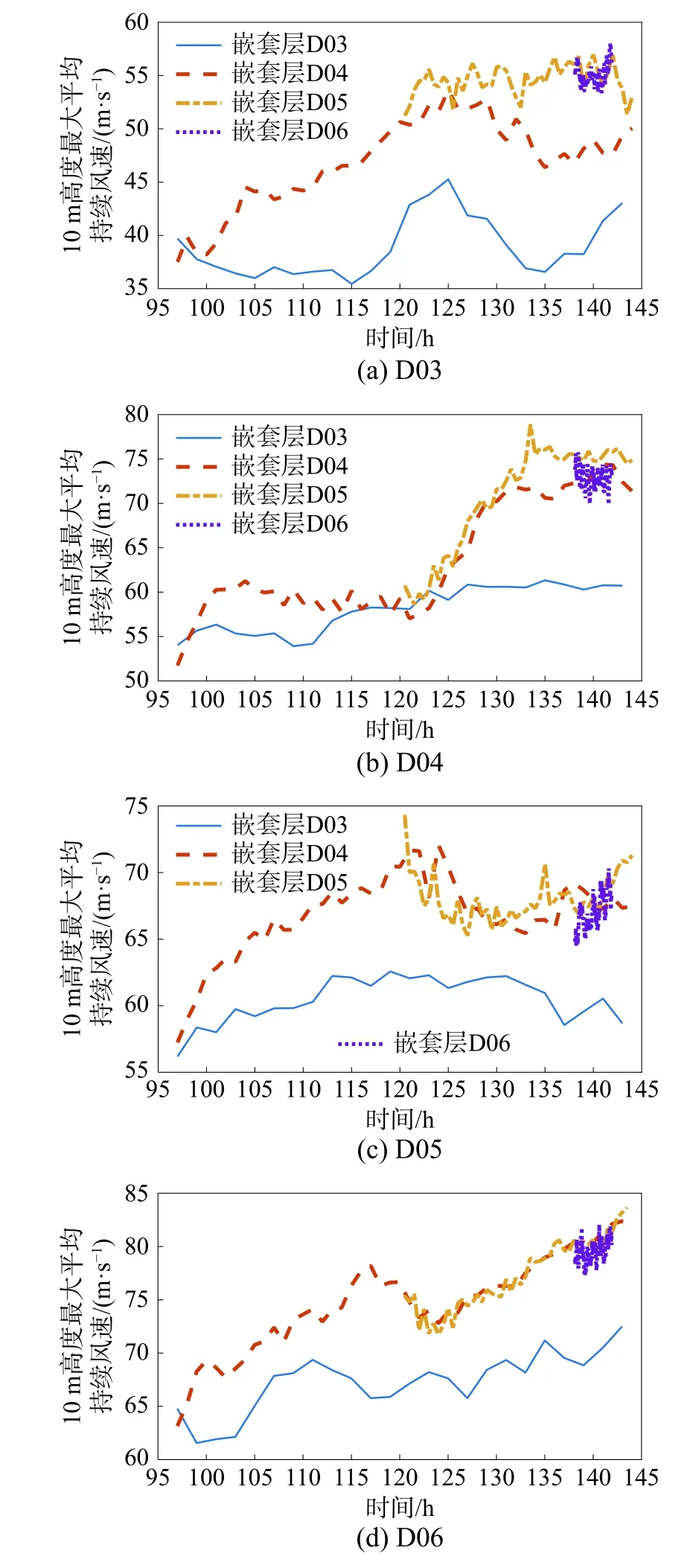
圖2 10 m 高度處最大平均持續風速Fig. 2 The maximum mean sustained wind speed at a height of 10 m

2.2.2 不同海表溫度對臺風風災害評估因子指標影響

本文開展了4 種不同海表溫度下理想臺風數值模擬，不同海表溫度下各嵌套層10 m 高度處最大平均持續風速分布如圖3 所示。隨著海表溫度升高，最大平均持續風速整體呈現增加趨勢。需要注意的現象是最大平均持續風速在SST-27 和SST-28 之間存在“交叉”現象(SST-27 最大平均持續風速穩態時刻大于SST-28)；按照傳統的單一采用最大持續風速來表征臺風強度和災害的原則，即得出SST-27 臺風強度和風災害程度均大于SST-28。

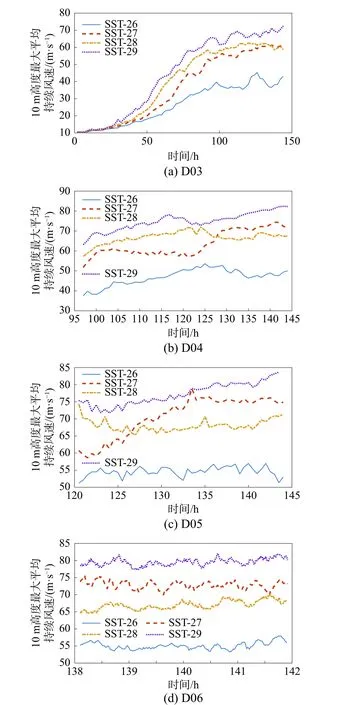
圖3 10 m 高度處最大平均持續風速Fig. 3 The maximum mean sustained wind speed at a height of 10 m

為探究SST-27 與SST-28 臺風風災害實際強弱程度，本文首先依據POWELL 和REINHOLD[13]提出的積分動能指標來計算不同算例不同嵌套層全臺風空間風災害程度，具體見圖4。結果表明：SST-28 相比SST-27，臺風風災害程度在各嵌套層均更強。這是因為積分動能指標同時考慮臺風強度和空間尺寸，雖然SST-28 最大平均持續風速小于SST-27，但是SST-28 具有更大范圍的較大風速區間。依據積分動能指標，隨著海表溫度升高，臺風風災害呈現增加趨勢，說明考慮臺風空間尺寸后，臺風風災害程度隨海表溫度增加而增加。另外，對于積分動能指標，各算例嵌套層D04、D05和D06 趨于一致。

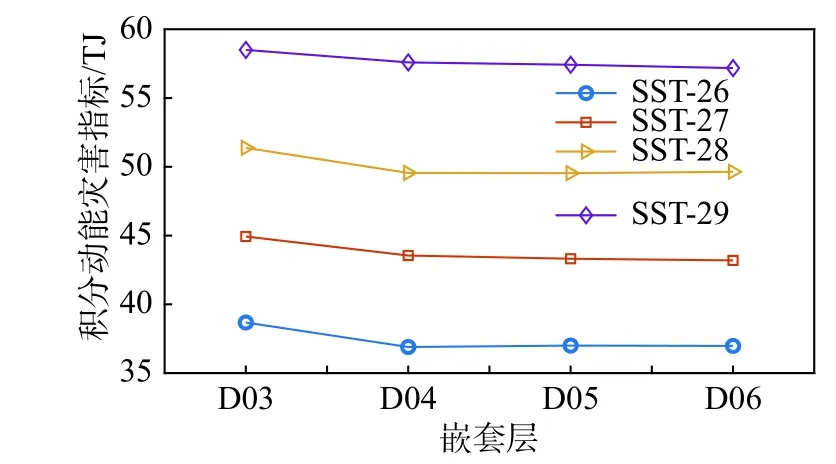
圖4 各算例各嵌套層積分動能災害指標表征( IKE>0TJ)Fig. 4 Integral kinetic energy disaster index characterization for each nesting level of each case ( IKE>0TJ)

本小節分析得出，單獨考慮風速大小評估臺風風災害程度存在一定的誤導作用，而考慮臺風空間尺寸能夠更加真實地表征臺風風災害程度。因此，接下來的研究中將重點探究如何考慮空間尺寸來表征臺風風災害。

3 面積積分方法

基于空間特性最直觀想法即是考慮整個臺風覆蓋范圍，將災害評估指標因子按照面積進行積分，這個思想與POWELL 和REINHOLD[13]提出的積分動能概念相同。對風災害評估指標因子D進行面積積分的方法為基于面積的風災害評估方法，得到的指標定義為Darea，其物理意義是當Darea等于1010% m2時，相當于10 km×10 km 區域內結構發生100%損壞或者在100 km×100 km 區域內結構發生1%損壞，因此，Darea代表的是相對代價或成本。通過對比不同臺風Darea大小，可以說明不同臺風在同一區域產生的風災害強弱程度。圖5 和圖6 為不同工況不同嵌套層在10 m 高度處基于面積積分風災害Darea評估結果。其中，圖5 對應積分面積大小為D06 區域，圖6 對應積分面積大小為D03 區域。本文分別采用基于D03和D06 區域進行分析是為說明臺風外圍小風速區域占比情況以及對風災害評估的影響程度。

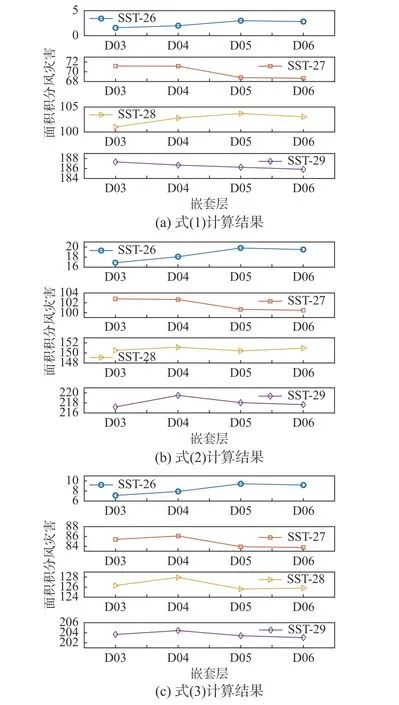
圖5 基于D06 面積積分的風災害評估結果 /( × 109)Fig. 5 Wind disaster assessment results based on D06 area integral

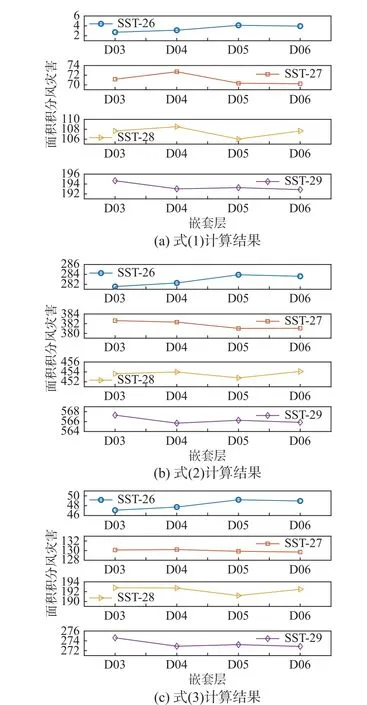
圖6 基于D03 面積積分的風災害評估結果 /( × 109)Fig. 6 Wind disaster assessment results based on D03 area integral

對于SST-27、SST-28 和SST-29 算例，無論D03、D04、D05 還是D06，平均持續風速均達到了60 m/s (如圖2 所示)，各嵌套層基于面積的風災害評估結果大小相似，可分別見圖5 和圖6。而對于SST-26 算例，因各嵌套層平均風速未達到60 m/s，風災害隨網格尺度減小呈現增大趨勢。因此，這里通過分析SST-26 算例在不同嵌套層風災害評估結果進行基于面積積分方法探究，具體的，對于式(1)，以D06 區域空間為積分面積各嵌套層之間增加比率依次為：20.63% (D04 相對D03，下同)、33.35% (D05 相對D04，下同)、0% (D06相對D05，下同) (圖5(a))；以D03 區域空間為積分面積各嵌套層之間增加比率依次為：12.64%、23.82%、0% (圖6(a))。對于式(2)，以D06 區域空間為積分面積各嵌套層之間增加比率依次為：6.39%、8.75%、0% (圖5(b))；以D03 區域空間為積分面積各嵌套層之間增加比率依次為：0.18%、0.54%、0%(圖6(b)))。對于式(3)，以D06 區域空間為積分面積各嵌套層之間增加比率依次為：9.73%、16.12%、0% (圖5(c))；以D03 區域空間為積分面積各嵌套層之間增加比率依次為：1.23%、2.91%、0% (圖6(c))。從中可以得出，以D03 區域空間為積分面積各嵌套層之間增加比率小于以D06 區域空間為積分面積各嵌套層之間增加比率。原因是D03 區域包含大范圍的小風速區間，而小風速對臺風風災害貢獻較小，因此對臺風風災害存在高估現象。具體而言，對于式(1)，高估8%～10%；對于式(2)，高估6%～8%；對于式(3)，高估8%～13%。以此說明，全臺風空間尺寸風災害評估存在一定的高估；同理可知，POWELL 和REINHOLD (2007)[13]提出的積分動能指標也存在相同問題。

上述分析對象是同一積分面積區域同一公式不同嵌套層風災害評估。這里進一步開展同一嵌套層同一公式下不同積分面積區域的風災害評估分析，具體為分別對比每個嵌套層區域在基于D03 和D06 面積積分風災害結果(圖5 和圖6)。式(1)結果在兩種區域空間標準下相差不大，說明臺風外圍小風速區域對式(1)計算結果影響較小；對于式(2)和式(3)，臺風外圍小風速區域對風災害計算結果影響較大。具體地，對于式(2)，SST-27、SST-28 和SST-29 算例D03 和D06 結果相差2.6 倍～3 倍；SST-26 算例結果相差17 倍。同樣，對于式(3), SST-27、SST-28 和SST-29 算例D03和D06 結果相差1.3 倍～1.5 倍；SST-26 算例結果7 倍。可得出小風速區間風災害在中等和強臺風占比最高可達61.5%～67.7%，弱臺風最高可達85.7%～94.1%。已有研究結果表明，臺風眼壁區是最具破壞區域，而外圍區域對結構破壞程度較小。對比區域D03 和D06 風災害結果可以看出，式(1)對區域尺寸敏感性最低，也即主要破壞集中在D06區域，符合物理認知。因此，以符合建筑結構設計規范的沿海或海上結構為對象，則式(1)在三個公式中物理意義最明確，最貼近實際自然情況，也最能表征臺風引起的結構風災害程度。但是，如若一些地區基礎設施抗風能力弱，式(2)或者式(3)可能會更適用。

4 引入切入風速的面積積分方法

上節分析發現，基于面積積分風災害評估方法對于風速小但尺寸大和風速大但尺寸小臺風風災害程度仍不能準確評估。因此，針對這兩種臺風工況，本文提出一種風災害評估解決方案，即引入切入風速概念，在基于面積積分風災害評估方法中僅將大于切入風速的風場部分用于風災害評估分析。

POWELL 和REINHOLD (2007)[13]將臺風風災害根據風速大小分為3 個級別，輕度風災害：平均風速在25 m/s～41 m/s；中度風災害：平均風速41 m/s～55 m/s；重度風災害：平均風速大于55 m/s。此外，工程結構如風力機正常工作運行風速范圍一般為3 m/s～25 m/s，當風速更大時風力機會開啟保護模式，也即停止運轉、葉片變漿，以減小風阻避免發生結構性損壞。基于上述原因，選取25 m/s 作為切入風速進行風速小但尺寸大和風速大但尺寸小臺風風災害評估應該是合理的，但基于本文提出的風災害評估指標因子D分析結果得出以25 m/s 作為切入風速時仍存在高估現象。這里不列出具體分析過程，僅給出結論：① 以同一積分面積區域同一公式進行不同嵌套層風災害評估，對于式(1)，高估2%～3%；對于式(2)，高估2%～4%；對于式(3)，高估3%～4%。② 以同一嵌套層同一公式進行不同積分面積區域風災害評估，式(1)結果在兩種區域空間標準下基本一致；對于式(2)，SST-27、SST-28 和SST-29 算例D03和D06 結果相差1.17 倍～1.29 倍；SST-26 算例結果相差1.50 倍。對于式(3)，SST-27、SST-28 和SST-29 算例D03 和D06 結果相差1.07 倍～1.14 倍；SST-26 算例結果1.38 倍。可以得出相較于未引入切入風速工況已顯著改善，但仍存在一定的高估現象。

為進一步改善風災害評估效果，本文認為達到臺風風速才會使得結構破壞，也即選擇32 m/s作為切入風速進行風速小但尺寸大和風速大但尺寸小臺風風災害評估，具體分析結果如圖7 和圖8所示，分別對應積分面積為D03 區域和D06 區域。

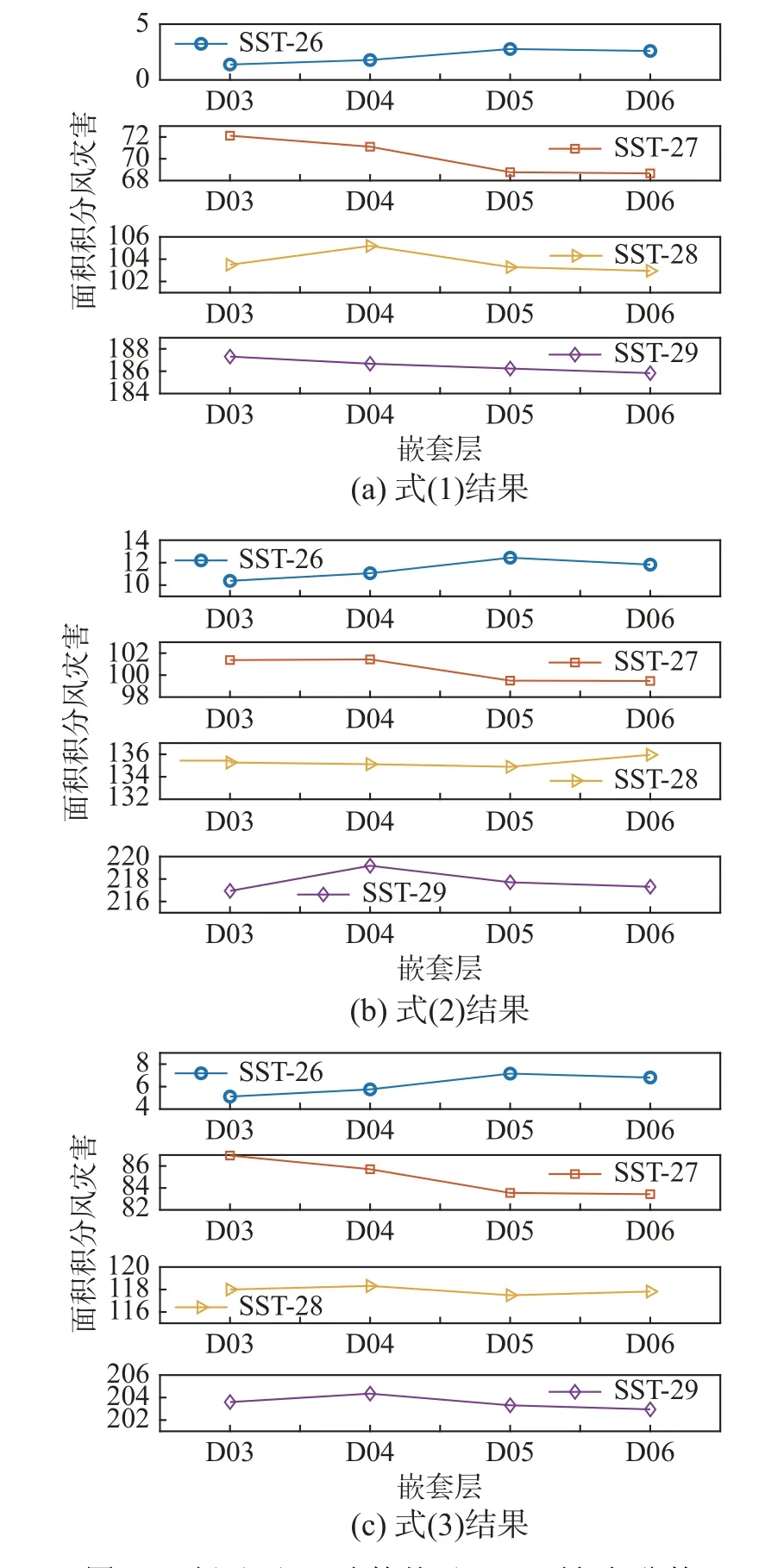
圖7 引入切入風速的基于D06 面積積分的風災害評估結果 /( ×109)Fig. 7 Wind disaster assessment results based on D06 area integral with cut-in wind speed

首先，引入切入風速后，對于式(1)，以D06區域空間為積分面積各嵌套層之間增加比率依次為：22.58%、35.56%、0% (圖7(a)；以D03 區域空間為積分面積各嵌套層之間增加比率依次為：23.27%、35.07%、0% (圖8(a))。對于式(2)，以D06 區域空間為積分面積各嵌套層之間增加比率依次為：6.12%、11.11%、0% (圖7(b))；以D03區域空間為積分面積各嵌套層之間增加比率依次為：9.30%、8.70%、0% (圖8(b))。對于式(3)，以D06 區域空間為積分面積各嵌套層之間增加比率依次為：11.11%、19.61%、0% (圖7(c))；以D03 區域空間為積分面積各嵌套層之間增加比率依次為：13.14%、18.11%、0% (圖8(c))。與前述未引入切入風速對比分析可得，引入切入風速對以D06 空間為積分面積結果影響不大，對D03 影響較大，可得出引入切入風速后以D03 區域空間為積分面積各嵌套層之間增加比率與以D06 區域空間為積分面積各嵌套層之間增加比率的相差比率顯著減小。這是因為，引入切入風速后，D03區域包含的小風速區間對風災害貢獻存在一定程度降低，以D03 空間為積分面積的風災害高估現象得到解決。

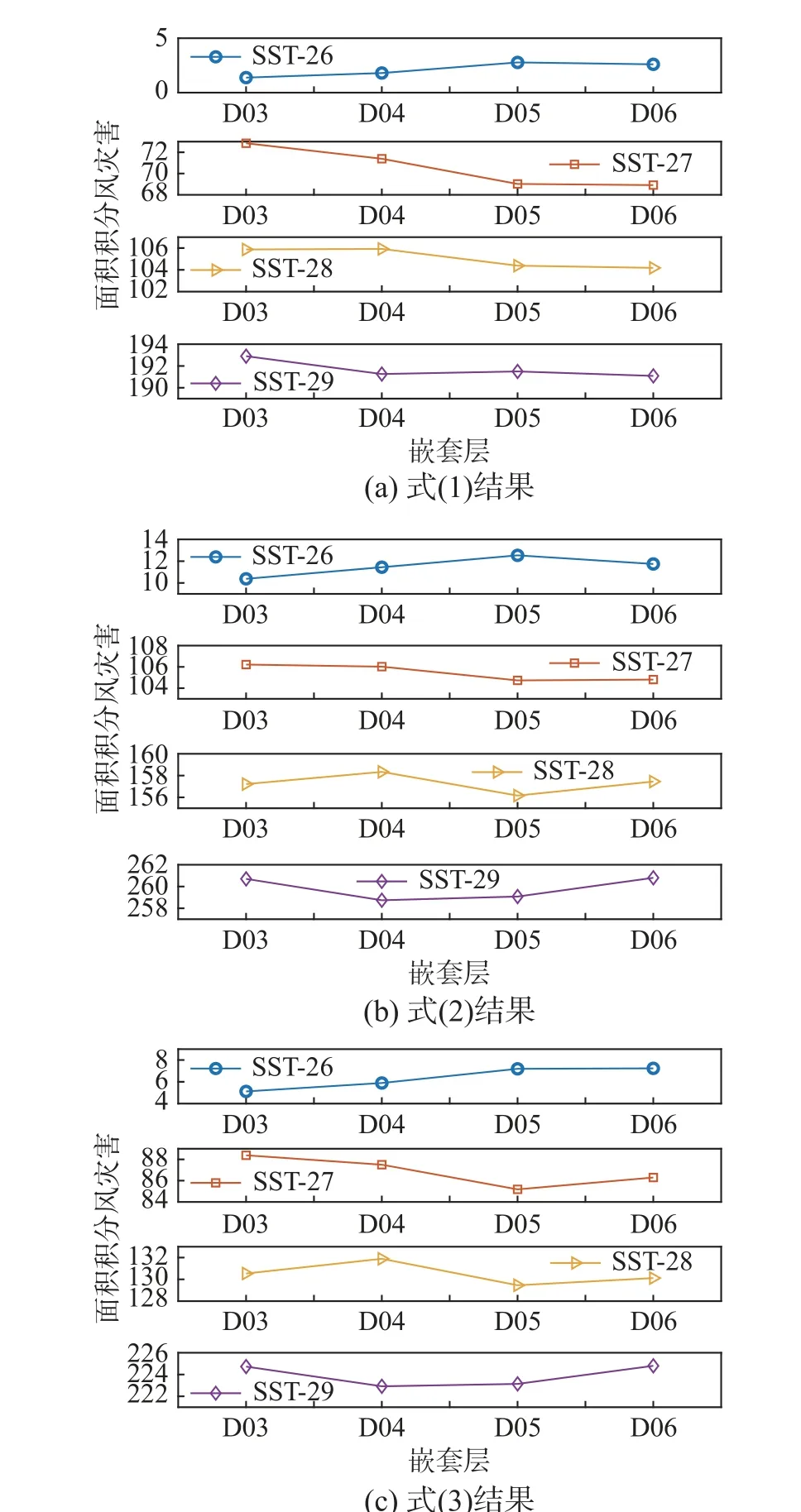
圖8 引入切入風速的基于D03 面積積分的風災害評估結果 /( ×109)Fig. 8 Wind disaster assessment results based on D03 area integral with cut-in wind speed

另外，對比分析引入切入風速后各嵌套層在基于D03 和D06 區域風災害面積積分結果(圖7和圖8)。同樣地，在兩種區域空間標準下式(1)結果相對式(2)和式(3)相差仍較小，最能真實反映臺風引起的結構風災害程度。具體的，對于式(1)，各算例D03 和D06 結果與上述未引入切入風速基本相同。對于式(2)，SST-27、SST-28 和SST-29算例D03 和D06 結果相差1.05 倍～1.19 倍；SST-26算例結果相差1.04 倍。同樣，對于式(3)，SST-27、SST-28 和SST-29 算例D03 和D06 結果相差1.02 倍～1.10 倍；SST-26 算 例 結 果1.02 倍。因此，引入切入風速后，三個公式在兩種區域空間的差距相對未引入切入風速結果顯著降低；小風速區間風災害在中等和強臺風占比最高為9.09%～16.0%，弱臺風最高為1.96%～3.85%。

綜上可知，引入切入風速概念，能夠很好地避免小風速區間占比過大但又對結構無實質損傷現象的發生。因此，通過引入切入風速概念，采用合適的切入風速可解決風速小但尺寸大和風速大但尺寸小的臺風工況風災害評估問題。也即，若采用基于面積積分臺風風災害評估方法，需要引入適當的切入速度，而非全風速空間。

5 結論

本文為探究基于空間特性的臺風風災害評估方法，開展了表征不同強度等級的四種不同海表溫度下理想臺風數值模擬研究。通過分析臺風風災害影響因子、基于面積積分風災害評估方法，以及尺度大強度小和尺度小強度大臺風風災害評估解決方法，得出以下主要結論：

(1) 不同網格精度和海表溫度是影響風災害評估指標因子的兩個因素。網格越精細風災害評估指標因子越大，且水平計算網格尺度為185 m 甚至555 m 時模擬結果即可表征臺風風災害。海表溫度越高風災害評估指標因子也越大，但是SST-27 和SST-28“交叉”現象說明僅考慮臺風強度表征風災害有誤導性。這促使開展基于空間特性風災害指標因子探究，并提出基于面積積分臺風風災害評估方法。

(2) 基于面積積分臺風風災害評估方法，能夠很好地解決僅考慮臺風強度出現的風災害“交叉”現象，SST-27 風災害在各嵌套層均小于SST-28。另外，得出千米量級以下網格尺度數值計算和雷達、衛星等監測設備精度的必要性。

(3) 但基于面積積分臺風風災害評估方法因對建筑結構破壞不起作用的小風速區間較敏感，不能較好地表征臺風強度大但尺寸小、強度小但尺寸大的風災害問題。針對此問題，本文提出的解決方法是設置適當的切入風速，從而使風災害高估現象得到有效解決。具體地，引入切入風速前，對于式(1)，高估8%～10%；對于式(2)，高估6%～8%；對于式(3)，高估8%～13%；引入臺風強度作為切入風速后，各公式基本無高估現象。

但從實際工程應用角度考慮，三維臺風空間風場不易捕獲。而臺風氣象實測資料中包含監測的最大風速、最大風速半徑、10 級風圈等特征量。因此，筆者正在進行的研究中將通過沿徑向臺風風速分布，對實際自然界結構破壞臺風風災害進行評估。

同時，針對如何將本文提出的風災害評估指標因子應用于工程實踐中，初步想法包含兩個層面：第一，與50 年一遇風速進行結構抗風設防一致，根據文中提出的風災害評估指標因子公式計算得出50 年一遇風災害指標因子大小；第二，依據本文創新點-考慮臺風空間特性進行風災害評估，結合歷史臺風數據和氣象數值模擬的多個臺風數據，進而獲得風災害指標因子空間分布圖，以此提出類似地震領域“烈度”概念，為區域風場災害程度提供合理依據。