函數思想在高中數學中的應用
安徽 石 舢
函數是高中數學中的一大主線,函數思想在非函數章節中有著廣泛的應用,利用函數思想解決相關問題有時會輕松很多.本文介紹了函數思想在高中數學中部分內容上的應用,以期幫助學生巧妙地解決相關數學問題.
1.在不等式中的應用
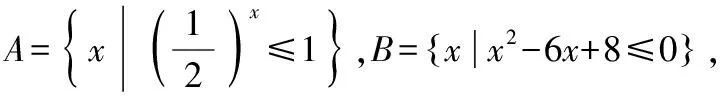
函數思想在不等式中有著廣泛的應用,除了在求不等式解集上的應用外,在不等式恒成立問題中也有著重要體現,而恒成立問題一般是求參數的取值范圍,在試題中分兩種情況存在:在R上求參數取值范圍和在給定區間上求參數取值范圍,不妨先分析前一種情況,如例1.
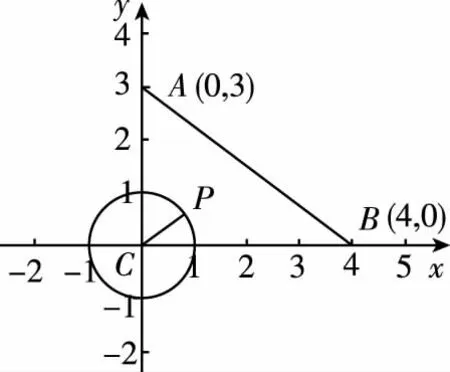
【例1】若不等式kx2+kx-1<0對一切實數x恒成立,則k的取值范圍為.
【分析】我們不妨令f(x)=kx2+kx-1,那么問題轉化為對?x∈R,都有f(x)<0,求k的取值范圍.此時,函數f(x)較為簡單,學生并不陌生,可直接對f(x)進行考查,這時我們需要對k進行分類討論,易知當k=0時滿足題意,當k≠0時,不等式中的恒成立問題便是直接對二次函數進行考查了,我們只需要確保二次函數圖象開口向下且與x軸沒有交點即可,像這樣的不等式恒成立問題,我們利用到了分類討論思想、函數思想和數形結合思想很容易求解.

【分析】有時我們考查的函數較為復雜,亦或是由于含有參數的原因,需要分類討論的情況較多,這時直接構造函數進行分析時可能較為煩瑣,如果參數可分離,將剩余部分看成一個整體,設成相應函數,再進行分析,可能會有意想不到的效果.下面看看用該方法解例1.

(1)當x2+x=0時,k∈R.



【分析】在例1中,我們發現方法2比方法1較為煩瑣,其原因在于x2+x的符號需要進行討論,倘若對于kf(x)>a(a≠0),知道f(x)的符號,那么采用方法2較為容易,而這種情況在給定區間上求參數取值范圍較為常見,因為區間給定,f(x)的取值范圍就知道了,不妨看看例2.

【解析】由(a-a2)x2+x-a+a2≤0?(a-a2)(x2-1)≤-x,

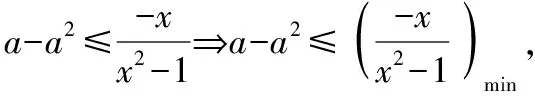

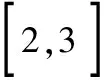
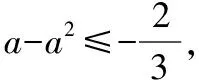
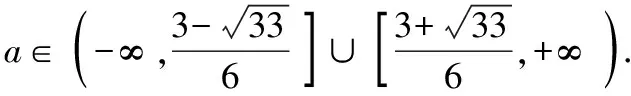

像上述不等式的問題,我們很容易聯想到函數,利用函數解決問題.
2.在比較大小中的應用
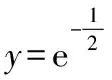
【例3】已知實數a,b,c滿足b+c=6-4a+3a2,c-b=4-4a+a2,則a,b,c大小關系是( )
A.c≥b>aB.a>c≥b
C.c>b>aD.a>c>b
【分析】兩個實數大小的比較,可用作差法或是作商法.通過觀察發現b+c和c-b都是關于a的表達式,易聯想到作差法比較a,b,c的大小,且若b和c能夠表示成a的表達式,則可將a-b或b-a,c-b或b-c,a-c或c-a看成是關于a的函數,然后進行分析.
【解析】由題意可知,b+c=6-4a+3a2①;c-b=4-4a+a2②.
①-②得,b=a2+1,故b-a=a2-a+1(將b-a看成是關于a的二次函數,易知函數開口向上,且Δ=1-4<0),故b-a>0,即b>a.
c-b=4-4a+a2=a2-4a+4(將c-b看成是關于a的二次函數,易知開口向上,且Δ=16-16=0),故c-b≥0,即c≥b.
故c≥b>a,故選A.
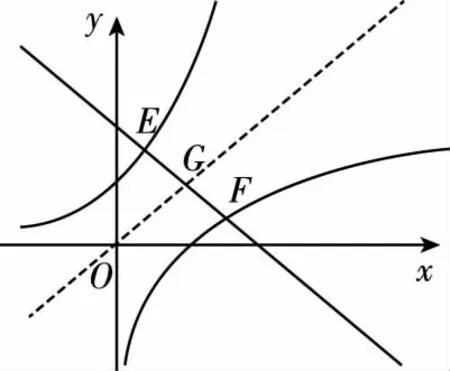
【例4】已知a,b是實數,且e 在比較兩個實數大小中涉及函數思想問題,有時不易直接看出需要構造的函數,這時還需解題者具備一定的觀察能力、分析能力,通過化歸與轉化思想,然后構造出相應函數,從而解決問題. 方程與函數有著密不可分的聯系,在人教版必修第一冊(A版)中將一元二次函數、方程和不等式放在一起作為第二章內容,正是因為他們有著密切聯系,對解題有幫助,且對學生日后解決復雜方程問題提供重要的數學思想——函數思想.在方程中,經常遇到方程有根問題、零點問題,均可構造相應函數,通過考查函數的性態解決問題,如例5. 【例5】方程ex+3x=0實數解的個數是( ) A.0 B.1 C.2 D.3 【分析】直接解方程ex+3x=0顯得十分困難,或是當下無法求解,若利用化歸與轉化思想,將題目改成函數f(x)=ex+3x有幾個零點問題,即函數f(x)=ex+3x與x軸有幾個交點的問題,將方程問題轉化成函數問題,可能會有意想不到的收獲. 【解析】設f(x)=ex+3x,則f′(x)=ex+3>0,故f(x)在(-∞,+∞)上單調遞增,又因為當x→-∞時,f(x)<0,當x→+∞時,f(x)>0,所以f(x)在(-∞,+∞)上有且僅有一個零點,則方程ex+3x=0在R上有且僅有一個實數根,故選B. 函數在方程中的體現除了利用函數本身的特性解相關方程問題之外,函數的圖象也是一種十分重要的工具,有時我們需要借助函數的圖象來解方程問題,在試題中也是常見的,如例6. 【例6】設a,b分別是方程lnx+x-2=0和ex+x-2=0的根,則a+b的值為. 【分析】直接求出a,b的值顯然是無法辦到的,觀察發現兩個方程均有x-2這個式子,那么將兩個方程通過變形,得到lnx=2-x和ex=2-x,我們可構造三個函數:y=lnx,y=ex,y=2-x,并將它們的圖象畫出來,從圖象上分析問題是否會發現“新大陸”? 從例6中可以看出,函數圖象在解題中的重要作用,從圖象上分析問題、解決問題就比較輕松,在例5中,我們也可將題目轉化為函數y=ex與y=-3x有幾個交點?畫出草圖后,發現只有一個交點. 在向量中,經常遇到求最大值、最小值以及取值范圍的問題,有關最值或是取值范圍問題一定是題目中存在某一量在變動,顯然是直接對函數進行考查.在向量中能夠發現函數的影子,無非是將有關向量知識點融入到函數中對學生進行考查,其本質還是函數問題. A.[-5,3] B.[-3,5] C.[-6,4] D.[-4,6]
3.在方程中的應用

4.在向量中的應用