雙二體幾何切面法及天梯地月轉移軌道分析*

童科偉，程炳琳，汪小衛

(1. 中國運載火箭技術研究院 研究發展部， 北京 100076; 2. 中國運載火箭技術研究院， 北京 100076)

雙二體軌道拼接設計方法在月球探測軌道設計中具有基礎性作用，國內外學者以雙二體軌道拼接法為基礎對月球探測軌道設計方法進行了大量的研究[1-8]。

在基于雙二體問題求解地月轉移軌道時，Battin、郗曉寧、黃文德、賀波勇等都不約而同地以入口點月心經緯度作為中間變量來拼接地球影響球內飛行軌道和月球影響球內飛行軌道[1-2,4-5,8]。這種基于月球影響球球坐標來描述入口點位置的方法比較直觀，但是沒有充分利用轉移軌道的物理意義。

對于著陸地點已知的奔月任務，賀波勇推導了一種類解析的改進雙二體模型，該方法與傳統的從地球計算到月球不同，在計算窗口時針對已知的月心軌道六根數逆向計算地月轉移軌道六根數，計算量極小[9]。

對于工程約束不明、具體探測地點不定的地月轉移軌道窗口計算問題，還需要按照傳統的計算量較大的搜索方法，進而得到一些運動特性。與常規的以入口點月心經緯度作為中間變量的雙二體拼接方法不同，本文提出一種直接基于軌道特征的地月轉移飛行軌道的幾何方法，物理意義明確，求解地月軌道更加直觀，通過兩次降維解耦操作，降低問題求解維數，進一步提升計算效率。

考慮到目前大多數計算機都是多核中央處理器(central processing unit, CPU)，最簡單的提高算力的途徑是采用并行計算，充分利用各核的計算能力，并行計算技術在國內外受到高度重視。并行程序設計編程語言通常基于消息傳遞接口標準(message passing interface, MPI)、OpenMP等，二者甚至已經分別形成了集群并行和單機多核并行領域的事實標準[10-13]。

本文以Java相關的多核并行編程技術為基礎[13]，設計了一種地月轉移軌道的多核并行計算方法，并應用于天梯地月轉移軌道計算與特性分析。按照國際天梯協會(international space elevator consortium, ISEC)的定義，天梯是一種把有效載荷從地球表面提升到空間的系統，該系統是一個長10萬千米的繩系，質心在地球靜止軌道(geostationary orbit, GEO)，并固定于地表的某個錨點。隨著爬升高度的變化，天梯攀爬器在電能作用下抬升高度并獲得地球自轉帶來的圓速度，從而使有效載荷獲得勢能和動能[14]。由于天梯位于赤道上空，軌道傾角受限，與常規月球轉移軌道設計有一定區別。本文以一種幾何切面法雙二體模型來分析天梯發射航天器進入月球轉移軌道的特性。

1 雙二體幾何切面法

雙二體假設下的地月轉移軌道計算也稱為圓錐曲線拼接法。本質上是以月球影響球為邊界, 將軌道分成多段來拼接：進入影響球前, 飛行軌跡為地心圓錐曲線(一般為橢圓)；在影響球內，飛行軌跡為月心圓錐曲線(一般為雙曲線)。對于自由返回軌道等任務，還需考慮飛出影響球后的飛行軌跡，其為地心圓錐曲線(一般也為橢圓)。在進入和離開影響球的兩個邊界點(一般稱為入口點和出口點)，將這幾段圓錐曲線拼接成完整的運動軌跡。

圓錐曲線拼接法的設計參數通常以月球影響球入口點/出口點在月心白道坐標系下的經緯度作為獨立變量，通過該經緯度來描述入口點/出口點的空間位置[1-2,4-6,8]。

采用傳統的圓錐曲線拼接法的設計參數計算轉移窗口時問題待求解參數的維度大，計算轉移窗口時的計算時間過長。對于在天梯系統出發這一類地月轉移軌道設計問題，由于出發軌道的傾角已知、升交點赤經(right ascension of ascending node, RAAN)也可求出，本文借助空間幾何關系把原始問題降維，從而大大降低求解問題的規模。其基本思想是：基于轉移軌道面和月球影響球的幾何關系來描述空間位置關系，地月/月地轉移軌道面與月球影響球必須相交(否則一定不可能被月球捕獲)。通過轉移軌道面切割月球影響球形成的幾何關系就可以描述地月/月地轉移軌道，結合Lambert原理就可以求解出所需的轉移軌道參數。這樣就把原來的三維球面搜索算法降維成了二維平面內切割月球影響球形成的圓上的搜索算法。另外本文的描述方式把地月轉移軌道求解問題解耦成平面內轉移軌道形狀計算問題以及轉移軌道空間定向問題，從而大大降低了問題求解維度。

1.1 轉移三角形形狀計算問題

對于從天梯出發的奔月任務來說，為了擴大任務窗口，可以適當允許出發轉移軌道有小傾角，以盡可能節約推進劑，比如要求i∈[-0.5°,0.5°]。由于天梯質心位于地球定點位置，相應的升交點赤經為：

Ω=Ω0+ωEt

其中，Ω0為初始點降交點赤經，ωE為地球自轉角速度，t為據初始點時刻。

如圖1所示，定義地心為E，月心為L，軌道面與月球影響球切割形成圓的圓心為O。轉移軌道在地球近地點出發，該點定義為P，到達月球影響球的入口點A。

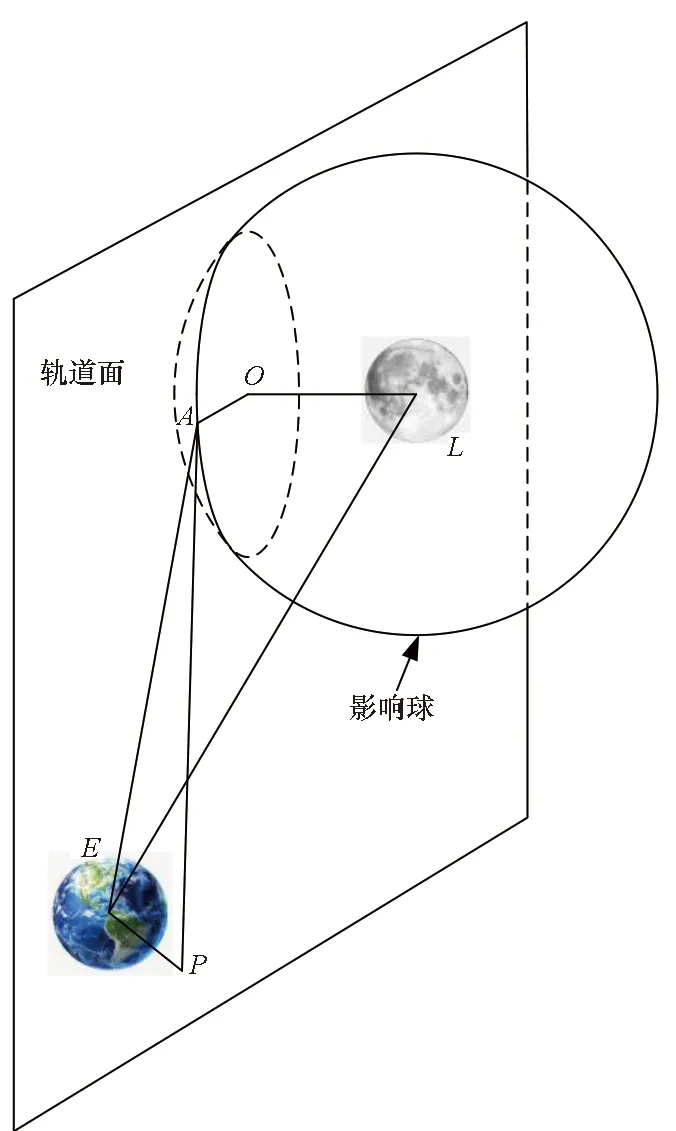
圖1 軌道面與月球影響球的切割示意圖Fig.1 Demonstration of section of orbital plane and the sphere of influence of moon

轉移軌道面與月球影響球切割的交線必然形成一個圓，該圓上各點到月心的距離等于影響球半徑rs，rs=66 200 km。轉移軌道面法方向或軌道動量矩方向nOL為：

nOL=[sinisinΩ,-sinicosΩ,cosi]T

(1)

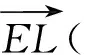
cos∠OLE|nOL·rL|/rL

(2)

其中，rL為地月距離。

由圖(1)所示的幾何關系可知，順行軌道(i,Ω)和逆行軌道(π-i,Ω+π)都滿足以上幾何關系(二者軌道面法向相差180°)，相應的式(2)取絕對值，可根據工程實際約束來選取。

l=rLcos∠OLE

(3)

地月轉移軌道面與月球影響球必須相交，否則轉移軌道與月球影響球沒有交點，就無法形成環月軌道。對應的數學約束條件就是：

l≤rs

(4)

發射窗口搜索時間區間出現在滿足式(4)的時間段，該約束條件可以極大地節約轉移窗口的計算量。

軌道面與影響球切割而成的圓半徑OA的大小r0為：

(5)

(6)

k-r0≤rEA≤k+r0

(7)

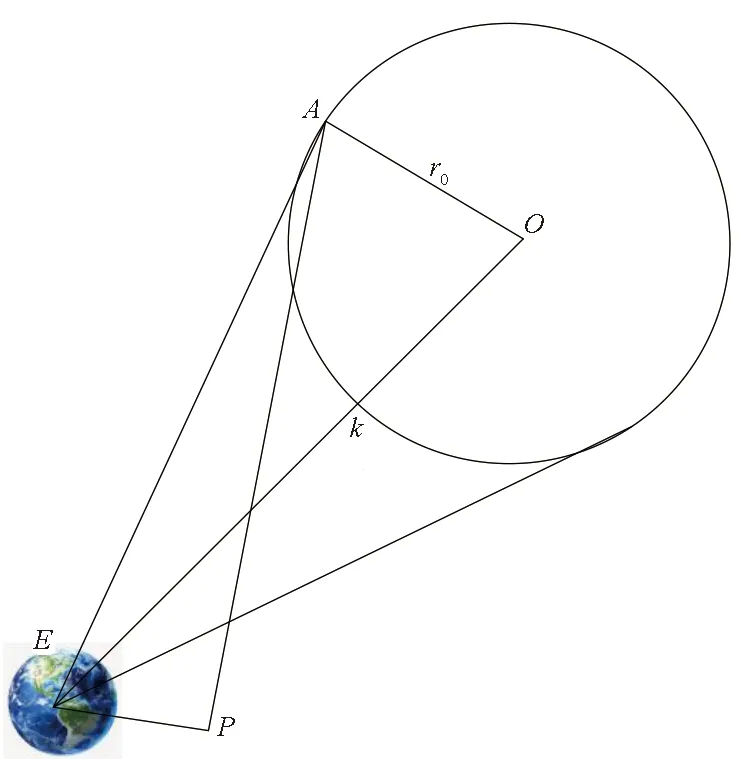
圖2 軌道面與月球影響球的截面平面示意圖Fig.2 Section plane of orbital plane and the sphere of influence of moon

由地月幾何關系，rEA取值范圍可擴大為：

rL-rs≤k-r0≤rEA≤k+r0≤rL+rs

(8)

已知地月平均距離為384 400 km，因此地月距離rL考慮一定余量就可以得到rEA的取值范圍，如取余量Δ=0.1可得：

(rL-rs)(1-Δ)≤rEA≤(rL+rs)(1+Δ)

即

286 380 km≤rEA≤495 660 km

(9)

在給定時間tPA內，從近地出發點P運行到入口點A的地月轉移軌道構成了一個Lambert問題。根據Lambert定理，地月轉移出發點P到入口點A的飛行時間tPA僅與軌道半長軸、兩點與地心距離之和rPE+rEA以及弦長rPA有關。又由余弦定理，給定rPE和rEA，則弦長rPA和真近點角θPA一一對應。因此地月轉移軌道問題轉化為已知tPA求θPA的問題。E、P、A確定了一個與轉移軌道相關的三角形，稱為轉移三角形。

賀波勇推導了tPA和θPA的導數關系。將tPA作為設計變量，用牛頓迭代法求解θPA[9]。本文的算例測試發現，該方法對初值較敏感，收斂性一般，計算量較大，且計算精度也不太高，為此改用Brent法求解。

Brent法在20世紀60年代，由阿姆斯特丹數學中心的Van Wijngaarden和Dekker等研究成功，并在1973年由Brent進行了改進。該方法特別適合于求解一維非線性方程的根，而無須提供函數的導數。該方法具有超線性收斂特性，又能夠保證二分法的收斂確定性。具體算法參見文獻[15]。

按照Brent算法，選擇tPA作為設計變量，求解θPA，二者的求解關系如下：

地月轉移軌道由近地點出發，存在如下關系：

rEA=p/(1+ecosθPA)

p=rEP(1+e)

可得到：

(10)

(11)

其中：p為半通徑；e為偏心率；a為半長軸。

至此由θPA、a、e不難求得轉移軌道飛行時間tPA，可以將求得的tPA與給定的轉移軌道飛行時間tPA0之差作為待求的一維非線性目標函數，對應的未知量θPA可由Brent法求解。

轉移三角形形狀求解問題在整個搜索過程中重復出現，但由本文模型的描述方式可知，該三角形與軌道傾角、升交點赤經和近地點幅角無關，因此該求解問題與整體窗口搜索算法解耦，可以把轉移三角形所有可能的軌道組合提前求解出來，在接下來的窗口搜索中就只需要匹配這些已知的轉移三角形，從而大大降低問題的搜索維度，節省計算量。此外轉移三角形形狀求解問題也從原來的三維影響球的球面經緯度搜索問題降維成為平面內圓上點的搜索問題，進一步節省了計算量。

1.2 轉移三角形的空間定向問題

1)對于如近地軌道空間站出發的地月轉移軌道，i和初始Ω0一般已知，則當時的Ω可由到達入口點時刻和飛行時間來決定，未知量為近地點幅角ω；

2)對于天梯奔月任務來說，天梯位于赤道上方，ω等于0°(順行軌道)或者180°(逆行軌道)，未知量為i。

以上兩種情況均可由Brent算法求解。

由地心慣性系到軌道系的坐標旋轉矩陣為：

其中：Lx(?)表示繞x軸旋轉?角度的坐標旋轉矩陣；Lz(?)表示繞z軸旋轉?角度的坐標旋轉矩陣；u=ω+θ為緯度幅角，其中θ為真近點角。

地心慣性系下的入口點位置矢量rEA為：

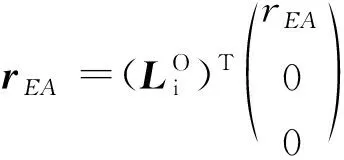
(12)

由圖1可知，rEA與月球位置矢量rL(由星歷計算)及入口點到月心的矢量rLA滿足如下幾何關系：

rLA=rEA-rL

而rLA的大小等于月球影響球半徑rs，則：

|rEA-rL|-rs=0

(13)

因此根據未知的ω或者i，由Brent算法預先判斷所求區間是否有解，再求解式(13)對應的一維非線性方程的根，就可以得到滿足條件的未知的ω或者i[15]。即：

1)對于i給定的轉移軌道，ω∈[0°,360°]，由式(12)和式(13)，根據已知的五個軌道根數，由Brent算法求解ω；

2)對于天梯任務，i∈[-0.5°,0°]和i∈[0°,0.5°]對應的逆行和順行軌道，同樣由式(12)和式(13)，根據已知的其他五個軌道根數，由Brent算法求解i。

然后根據式(1)～(6)計算轉移三角形數據庫中待評估的轉移三角形是否滿足式(7)。

以上求解軌道面參數的過程稱為轉移三角形的空間定向問題。

以上求解出了地月轉移段軌道六個軌道根數，還需要進一步判斷該軌道進入月球影響球被月球捕獲以后形成的環月軌道是否滿足給定條件。此時需把地心慣性系下的入口點處的矢量rLA和vLA轉換到月心白道系下[2]：

M=Lz(uL+π)Lx(iL)Lz(ΩL)

其中：M為地心慣性系到月心瞬時白道系的旋轉矩陣。上式中的上標L表示月球相關的參數。

基于上式求得的月心系下的位置和速度，就可以求得月心段繞月軌道參數，之后可以判斷是否滿足需要的環月軌道條件，比如環月軌道高度約束等。

以上是普通地月轉移軌道的求解流程。對于載人航天任務常用的自由返回軌道，可基于對稱性原理，進一步求得月地轉移段軌道參數，再判斷是否滿足載人航天任務常用的自由返回軌道約束條件，如返回地球時的近地點高度、再入角等。本文只計算一般的地月轉移軌道，自由返回軌道求解的具體流程可參考Battin[1]、黃文德[4-5]、賀波勇[8]等的報道。

2 天梯奔月解法

2.1 CPU并行計算技術簡介

當前CPU主頻的提升已經明顯遇到了瓶頸，計算機硬件界主要關注如何發展多核CPU。目前民用CPU已經擁有十多個核心。針對CPU核心數越來越多的現狀，科學計算必須考慮并行/并發程序設計，避免浪費計算資源。

并行計算一般可分為計算密集型、數據密集型、網絡密集型[10]，本文主要關注計算密集型計算。1994年誕生的MPI已經成為集群并行程序設計事實上的標準。1997年誕生的OpenMP已經成為單機多核并行事實上的標準[10]。本文的并行程序主要針對單機多核并行架構，而單機多核圖形處理器(graphics processing unit, GPU)加速并行架構和多機多核并行架構不在本文考慮。常用的并行分解技術有兩種：遞歸分解和數據分解[11-12]。本文著重關注單機CPU并行程序設計，并主要采用數據分解的方式來設計并行程序。

本文綜合考慮到可移植性、編程方便性、程序穩健性等，避免采用復雜的MPI，而是采用Java語言，并行計算程序設計基于Parallel Java 2 Library(PJ2庫)[13]。

PJ2庫是RIT(Rochester Institute of Technology)的Kaminsky教授開發的Java語言的并行計算調度庫，并應用于RIT計算機學院的超級計算機集群上。其主要設計思想是簡化并行計算程序設計的難度，特別是避免使用復雜的MPI，能夠極好地適用于單機CPU、GPU并行以及分布式集群異構并行計算。PJ2庫有五種CPU核心并行調度機制：Fixed、Leapfrog、Dynamic、Proportional、Guided。后四種調度機制代表了當前常見的先進并行調度機制，具體介紹參見文獻[13]。本文選擇Dynamic調度機制作為示例。

2.2 天梯地月轉移軌道窗口計算并行設計

天梯系統的基本組成如圖3所示，主要包括天梯繩索、地球表面節點、GEO節點、頂點錨、繩索攀爬器、地球表面運輸系統和運營中心[14]。

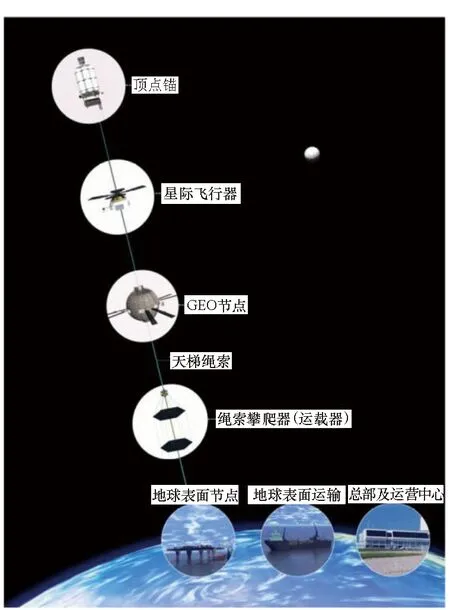
圖3 天梯系統組成示意圖[15]Fig.3 Composition of space elevator system[15]

天梯繩索是天梯最重要的組成部分，其主要功能為向攀爬器提供依附的途徑，使攀爬器能夠沿著纜繩從地表節點進入空間，同時其還要平衡整個天梯的重力與系統繞地球轉動形成的離心力；攀爬器為運輸有效載荷進入空間的運載器，其沿著繩索爬升，進入軌道預定位置后將有效載荷釋放；地球表面節點和頂點錨分別位于繩索的兩端，起到固定繩索位置、調整繩索姿態的功能。整個天梯的質心設置在GEO節點位置，這樣整個天梯系統就以地球的自轉速度圍繞地球旋轉，從而保證天梯與地面相對靜止[14,16]。

由于天梯從地表一直延伸到GEO更遠端，在執行行星際發射任務時，在天梯不同的高度釋放可以獲得不同的能量。比如，在天梯遠端頂點錨處(距離地心100 000 km)釋放甚至無須施加速度增量就可以飛往火星[16]。本文設計的從天梯飛往月球的轉移軌道算法，重點解決在天梯哪一高度釋放才能以最小的代價飛往月球。

本文假定天梯初始位于升交點赤經60°赤道上空。轉移軌道約束地月轉移軌道真近點角差θPA<π，近月點軌道高度為50 km≤rH≤1 000 km。考慮到2025年3月白道面與赤道面相對夾角達到最大值，約為28.72°，本文窗口計算的時間段取為2025年3月。

本文采用基于數據分解的并行方式，主要設計兩級并行算法：轉移三角形形狀并行計算問題和轉移三角形的空間定向并行計算問題。具體流程如圖4所示。

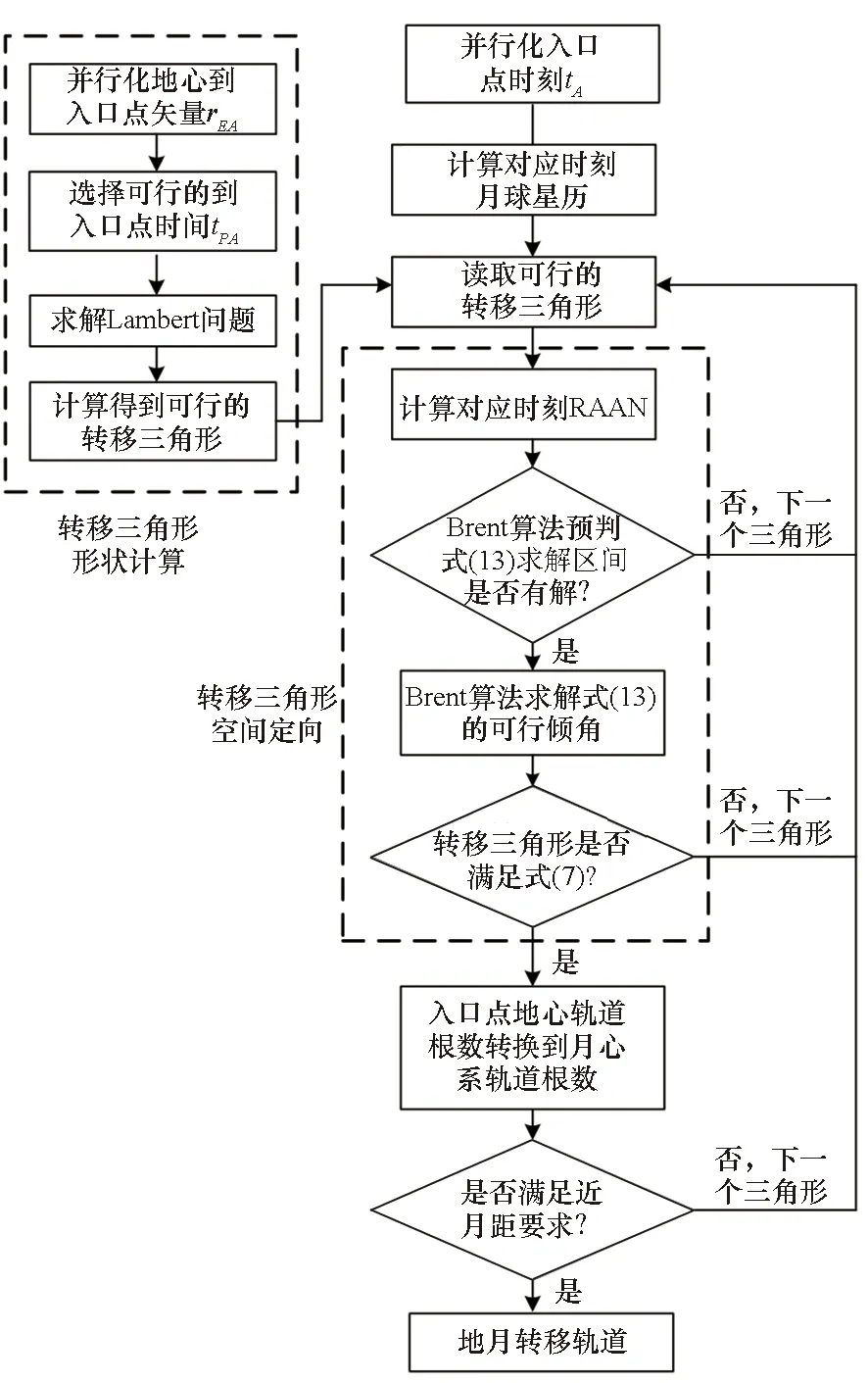
圖4 軌道設計流程Fig.4 Flow chart of trajectory design

第一個問題是轉移三角形形狀計算問題并行化：在初估轉移軌道特性時，rEA根據式(9)均勻選擇若干個點作為并行化設計參數，從近地點出發飛行到入口點的飛行時間tPA取30～170 h，基于Brent算法求解轉移三角形的真近點角，求得的結果存儲下來用于下一個子問題的搜索。

第二個問題是轉移三角形的空間定向問題并行化：天梯地月轉移軌道窗口計算時，以到達入口點時刻tA作為劃分并行顆粒度的設計變量，計算1個月的時間周期。以到達入口點時刻作為并行顆粒度劃分的主要好處是可以在并行計算之前計算好tA時刻的月球星歷。在計算空間定向時，軌道傾角i∈[-0.5°,0.5°]。在前一問題中求得的滿足約束的轉移三角形數據庫中，求解滿足式(13)的Brent子問題，從而求解出對應的轉移軌道空間定向參數軌道傾角。然后判斷所求得的軌道是否滿足地月轉移軌道條件，如果滿足則找到一條可行的轉移軌道。

2.3 天梯奔月窗口計算結果

下面分別計算GEO點釋放和天梯遠端頂點錨處釋放奔月的計算結果，分別如圖5和圖6所示。本文的算例中，采用一臺Windows 10系統的電腦(AMD 3700X八核十六線程CPU，主頻3.6 GHz，內存8G)，rEA取500個點，tPA間隔取0.2 h，tA間隔取10 min，并行計算在天梯GEO點釋放時1個月的奔月窗口需要437.57 s，串行計算需要3 040.32 s，并行加速比為6.95。

由圖5和圖6的計算結果表明，從天梯奔月每月內存在兩次窗口，每次窗口持續4～6天。對于奔月任務，天梯頂點錨處釋放所需的速度增量反而比在GEO節點直接奔月所需的速度增量大，這主要是由于在遠端頂點錨處釋放的地月轉移軌道獲得了過多的能量，此能量甚至能飛行到火星，但不適合用于月球軌道轉移。為了詳細計算窗口，還需要把rEA、tPA和tA的間隔取得更密集一些，但這里用于了解轉移軌道的特性已經足夠。

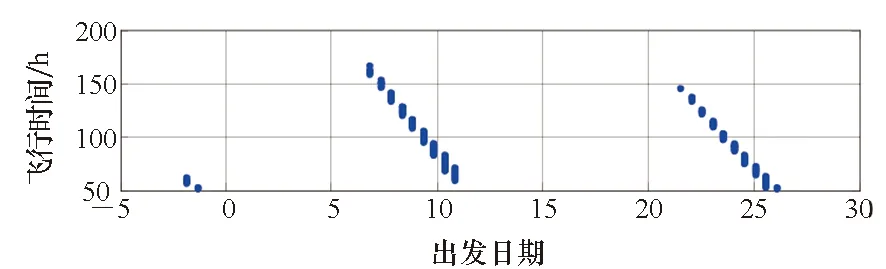
(a) 飛行時間結果(a) Results of flight time

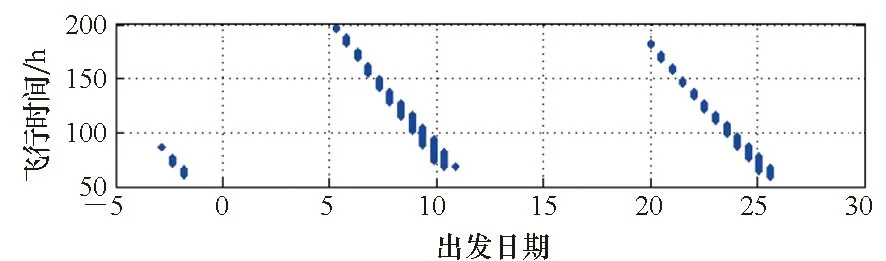
(a) 飛行時間結果(a) Results of flight time

為尋找到底在何處釋放可以以較小代價飛往月球，計算了天梯不同軌道高度釋放的奔月窗口，計算結果表明：在天梯距地心51 000 km處釋放進入地月轉移軌道，所需要的速度增量較小，所需速度增量如圖7所示。在此處釋放飛行器獲得的相對地心慣性系的線速度為3.719 km/s。

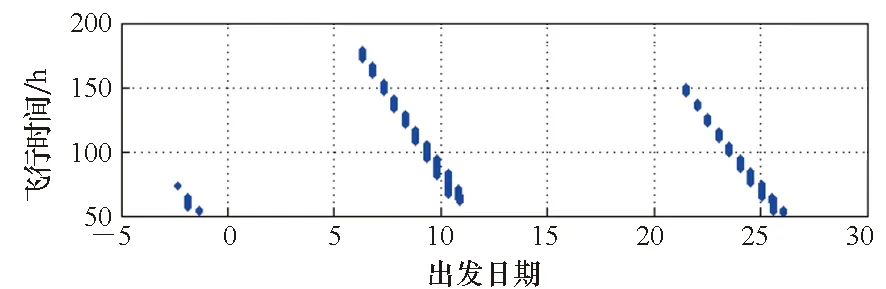
(a) 飛行時間結果(a) Results of flight time

為詳細研究從地心距51 000 km處釋放的地月轉移軌道特性，rEA取2 000個點，tPA間隔取0.1 h，tA間隔取1 min，并行計算天梯在GEO點釋放時1個月的奔月窗口需要30 220.12 s(合503.7 min)。

如圖8所示，在距地心51 000 km處的天梯奔月環月軌道傾角分布在10°～170°之間。

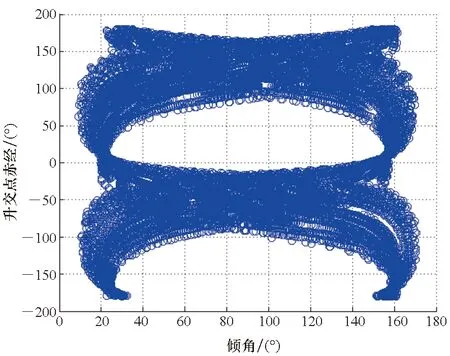
圖8 月球軌道傾角與升交點赤經Fig.8 Inclination and RAAN of Moon orbit

天梯地月轉移軌道的月球影響球入口點如圖9所示，在月球影響球上西半球，在南、北緯度均有分布。

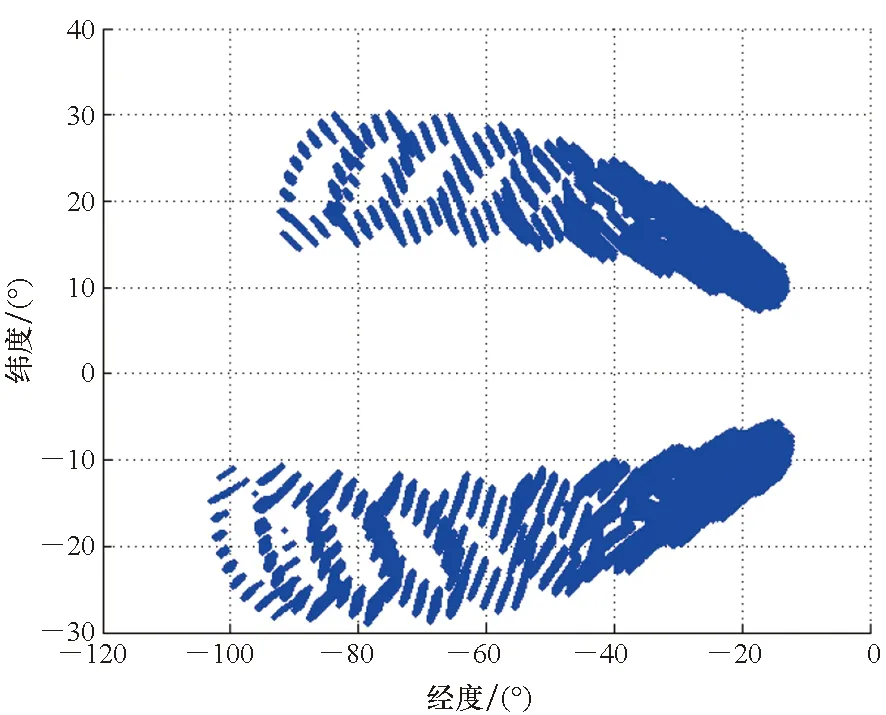
圖9 入口點經緯度分布Fig.9 Latitude and longitude of entry point

以尋找到的速度增量最小的轉移軌道為例，輸入STK進行驗證，計算得到的轉移軌道根數如表1所示，到入口點飛行時間111.9 h，入口點對應歷書時儒略日(對應STK的JED時間)為2 460 747.973 611 11，求得的最小速度增量為0.855 m/s，近月點高度為517.040 km。

表1 地月轉移軌道入口點根數

基于商業軟件STK的Astrogator模塊進行驗證，STK/Astrogator在地球段和月球段軌道預報器分別選地球點質量和月球點質量模型，STK計算得到的近月點高度為517.645 km。本文計算結果與之接近，顯示了本文算法的正確性。設計結果如圖10所示。

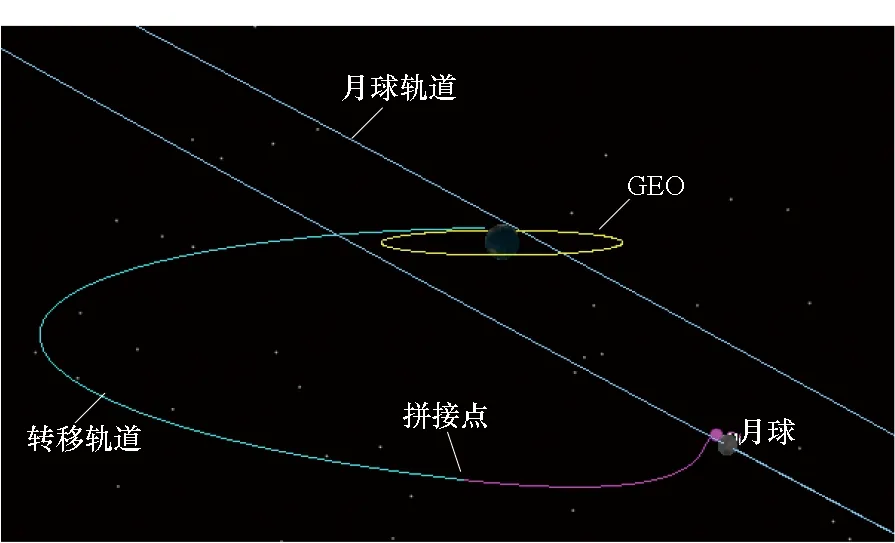
圖10 天梯地月轉移軌道Fig.9 Earth-Moon transfer orbit from space elevator

3 結論

本文提出一種基于飛行軌道面參數描述地月轉移軌道的雙二體模型表達方式，避免采用傳統的基于月球影響球入口點經緯度的描述方式，該表達方式由軌道定義出發，通過地月幾何關系來表述，更加明確直觀。通過表述方式的轉換把原來的三維球面搜索算法降維成為二維平面內圓上的搜索算法，結合一維非線性方程求根算法Brent算法和Lambert原理，可以高效地求解地月轉移軌道的形狀參數。

通過合理的解耦分解，將原始的軌道窗口多變量搜索問題進一步分解為兩個子問題：一個為轉移三角形形狀計算問題，通過轉移軌道形成的三角形幾何關系，結合Lambert原理求解出轉移軌道的形狀參數(半長軸、偏心率及真近點角)；另一個為轉移三角形的空間定向問題，基于已求得的轉移軌道形狀數據匹配搜索可行的轉移軌道，確定剩余的三個軌道面相關參數。最后為了加速窗口搜索過程，充分發揮多核計算機算力，形成一種轉移三角形形狀計算問題和空間定向問題的兩級并行算法。

基于本文的并行圓錐曲線幾何切面法，計算了天梯不同高度進行奔月任務的軌道窗口，結果表明：

1)在天梯遠端釋放執行奔月任務效果甚至不如在GEO點直接釋放的效果。

2)在距地心51 000 km左右釋放執行奔月任務所需的速度增量極小。

3)天梯出發的奔月環月軌道軌道傾角分布在10°～170°之間。入口點在月球影響球上西半球，在南、北緯度均有分布。

4)計算天梯奔月1個月的發射窗口，本文的兩級并行算法加速比達6.95。