車載多接入邊緣網絡中聯合資源分配和動態任務卸載方案*
薛建彬,安 悅,關向瑞,安亞寧
(蘭州理工大學 計算機與通信學院, 甘肅 蘭州 730050)
隨著移動網絡和物聯網技術的快速發展,專家預測:至2022年,汽車產業年銷量將達到600萬輛,全球汽車電子市場規模達3 800億美元,繼續呈加速增長態勢,智能網聯車熱潮已經襲來[1]。車輛激增涌現出了越來越多的時延敏感型和計算密集型的新型應用,例如自動駕駛、車輛社交網絡[2]和交互式游戲[3],為了應對不斷激增的數據流量和海量的設備連接,5G將滲透在未來生活的各個領域。車聯網技術與5G的落地應用,將為未來無人駕駛汽車提供可靠的技術支持,并將車聯網帶入一個新時代——無人駕駛時代。但是,這些新型應用給人們的生活帶來巨大便利的同時,大量的計算密集型應用會消耗更多的能量,給車載終端造成巨大的壓力[4]。此外,由于移動車載終端的計算資源有限,會增加消息處理的時延[5],這對車聯網技術的研究產生了巨大的挑戰。
面對這些挑戰,提出了支持多接入邊緣計算(multi-access edge computating,MEC)[6]的車載網絡架構。MEC服務器有強大的計算和存儲能力[7],基于MEC的解決方案,可以提供低時延、高帶寬并切合各應用場景的計算處理能力,具有很強的適用性,在這種協作架構下,車輛產生的任務可以卸載至路邊基礎設施單元(rode side unit,RSU)上的MEC服務器執行或者卸載至通信范圍內的其他車輛上處理,從而節省了傳輸時延和處理能耗,解決了車輛自身計算資源不足的問題[8]。
針對車輛計算資源不足的問題,建議將車輛任務卸載到其通信范圍內的其他車輛執行,考慮到車輛的移動性,在動態網絡下定義了一個風險函數來評估任務卸載失敗的可能性,并聯合系統風險提出了卸載效用函數。
1 相關工作
隨著以大數據為主要特征的各種先進技術在交通領域的應用,車聯網成為必然的發展趨勢。然而現今的車載設備有限的計算和存儲能力難以滿足大量高計算需求和低時延的限制,因此如何平衡應用時延高要求和車載終端計算能力,成為近些年研究的重點。多接入邊緣計算作為5G演進的關鍵技術,有助于克服車聯網領域中的發展瓶頸,為其發展提供有力支持。
針對車輛自身資源不足的問題,Hou等[9]提議將道路空閑車輛作為基礎設施,讓這些車輛提供卸載所需的計算資源。此外,文獻[10]引入了M/M/1排隊模型,設計了一種基于MEC負載狀態的預測性卸載策略,通過車與車通信方式進行任務卸載。文獻[11]不僅考慮將車輛產生的任務卸載至邊緣服務器,還進一步把任務劃分為可分割和不可分割,再分別進行卸載,以減少系統能耗。
前期研究任務卸載的目的是為了優化終端設備的能耗或者節省任務處理時延,但隨著研究的深入,在計算卸載過程中,除了上述優化目標外,還有許多學者研究了卸載過程中的無線電資源分配和計算資源分配[12]。例如,Wang等[13]在考慮系統總收入的條件下,聯合優化卸載決策和資源分配,以提高無線網絡的性能。此外,車聯網絡的服務質量和網絡成本也值得重點關注。文獻[14]提出了一種時延預測的組合方式,將任務自適應地卸載到MEC服務器,節省了計算成本。Si等[15]將車輛視為邊緣節點,利用車輛的潛在資源,減輕了網絡中的數據擁塞問題,提升了用戶的服務質量。
總的來說,大部分已有研究將任務卸載處理可以節省成本[16],或提高用戶的卸載效用[17],能夠彌補車輛自身資源匱乏的缺點。但這些方案都有一些局限性,以上研究都假設系統是準靜態的,并沒有考慮到車輛速度過快導致車與車或者車與基礎設施通信過程中連接中斷的問題[18]。一旦在任務卸載期間車輛或是MEC服務器與產生任務的終端車輛斷開連接,將會增大網絡時延和能耗成本。因此,為了提高網絡性能,在車輛卸載過程中,應考慮到車輛的移動性對系統的影響。
2 系統模型

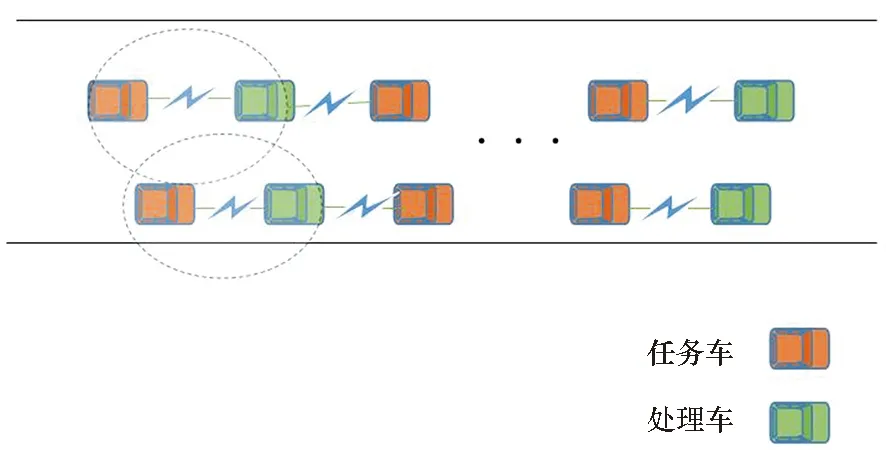
圖1 基于V2V通信的計算任務卸載Fig.1 Computing task offloading based on V2V communication
2.1 本地計算任務模型
(1)
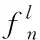
(2)
其中,ε為能量系數,它的值取決于芯片結構。
2.2 任務卸載模型
任務節點n卸載它的任務Kn到其中一個處理車輛j,產生的延遲由三部分組成:傳輸延遲,在處理節點的計算延遲,輸出結果回傳延遲。但是,由于輸出數據遠小于輸入數據,因此,第三部分的延遲經常可以忽略。
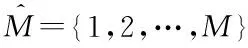
(3)
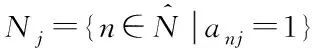
(4)
其中,hnj為任務車輛n和處理車輛j之間的信道增益,pn為任務車輛n的發射功率,σ2為背景噪聲方差。
則上行鏈路發送任務Kn的時間為:
(5)
任務在處理車輛處花費的時間為:
(6)
(7)
則卸載的總時延為:
(8)
上行鏈路的能量消耗為:
(9)
2.3 卸載風險模型
定義當卸載時間大于車輛之間連接時間為風險。設計一個風險評估模型來估計車輛卸載失敗的可能性,風險被公式化為卸載時間與車輛連接時間的比例。
(10)
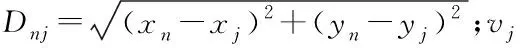
2.4 卸載效用模型
定義卸載效用函數為:
(11)
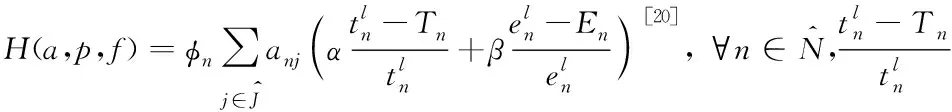
3 問題建模和解耦
3.1 問題建模
對于給定的卸載決策和資源分配,定義系統的卸載效用為所有用戶卸載效用的加權和。本節將優化問題公式化為混合整數非線性規劃(mixed integer nonlinear programming, MINLP),目標函數為:
(12)
(13)
(14)
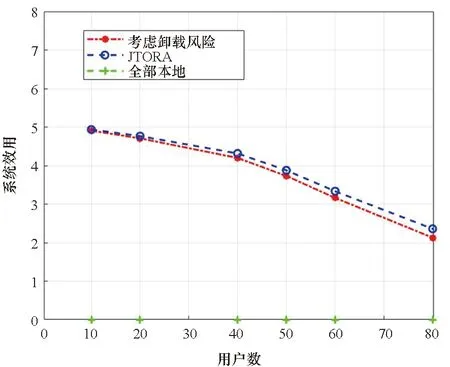
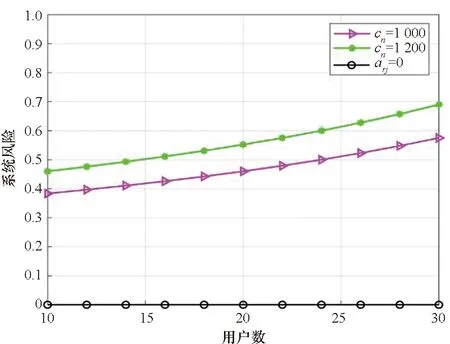
0 (15) (16) (17) 約束式 (13)是一個二進制卸載變量,表示任務可以在本地計算,也可以卸載到處理車輛執行。式(14)表示一個任務至多卸載至一個處理車輛執行,式(15)表示傳輸功率約束,式(16)表示每個卸載任務都應該分配計算資源,式(17)表示分配的總的計算資源應該在處理車輛的服務能力之內。 給定一個滿足約束式(13)、式(14)的任務卸載決策,整理可將目標函數重寫為: (18) 對于給定的卸載決策,式(18)中的第一項為常數。 其中 (19) 所以目標變成了 (20) 根據式(8)、式(9)、式(19)。可以得到 (21) 3.2.1 功率分配問題 s.t. 0 (22) s.t. 0 (23) 引理1達到最優值v*的條件是,當且僅當 =0 (24) 該定理的證明可在文獻[21]中得到。 上述定理表示問題P1可以通過它的等價問題式 (24)得到。此外,由于v*一般是未知的,故用v代替[22],如算法1所示。 問題式(23)可以改成以下形式: 0 (25) 為了解決P2,注意到問題P2為凸函數和線性函數的加權和,同時約束條件為凸條件,因此問題P2為凸函數[23]。 該問題滿足斯萊特條件,可以使用拉格朗日對偶分解和梯度下降法來解決[24]。 利用拉格朗日乘子法可將問題轉化為: (26) 該問題可以通過一個主問題和多個子問題的迭代來解決[24]。 子問題為: (27) 拉格朗日函數為: (28) 其中,k=(k1,k2,…,kNoff)≥0。通過KKT(Karush-Kuhn-Tucker)條件,求函數L(p,k)對于pn的微分,可以獲得每個用戶的最優傳輸功率分配。 (29) 算法1 迭代功率分配解決P1 主問題通過拉格朗日乘子來解決,利用梯度下降法更新拉格朗日乘子,k的表達式為: (30) 3.2.2 計算資源分配問題 (31) (32) (33) 注意到式(32)~(33)兩個約束條件都是凸條件,將目標函數P3用Υ(,Α)來表示。Υ(,Α)關于fnj的二階導數為: (34) 因此P3是一個凸優化問題,可以用KKT來解決。 (35) Υ( (36) 證明:問題P3的拉格朗日函數為: (37) γ=(γ1,…,γj)是拉格朗日乘子,對fnj求一階導數,可得: (38) 令式(38)等于0 ,求解出fnj,然后可得到最優的計算資源分配。 (39) (40) (41) 把式(41)代入式(39)可得: (42) 最后,目標函數P3可表示為: Υ( (43) 3.2.3 聯合任務卸載調度和資源分配 在上述分析中,對于一個給定的卸載決策,獲得了功率分配和計算資源分配,根據式(18)、式(21)和式(36)可得: (44) (45) (46) 其中,p*可以通過算法1 獲得,F*可以通過式(35)得到。 原始問題可重寫為: (47) 解決問題式(38)的一個直接方法是窮舉所有可能的卸載決策,進而得到最優的卸載決策,但此種方法復雜度為Ο(2n),其中n=N×J,顯然,使用窮舉法是不切實際的,因此提出一種次優卸載決策的方法來降低復雜度[25]。程序初始時,假設卸載集合=?,找到效用最大的集合,如果存在一個決策anj∈,將它刪除后集合的效用比刪除之前的集合效用大,那么執行刪除操作,從集合中刪除這個決策,直到再也找不出這樣的決策就停止刪除操作;如果存在一個決策anj∈Q/,將該決策加入集合中,使得系統效用的值變大,那么執行交換操作,直到再也找不出這樣的決策,程序結束。最后,找到了使系統效用最好的卸載決策集合,具體步驟如算法3所示。 圖2(a)~(c)所展示的是用戶數和系統效用之間的關系,將用戶數逐步增加,并在三種不同工作負載的情況下進行比較。從圖2(a)~(c)可以看出,隨著任務量的增加,所有方案的性能也顯著增加。這是因為,當任務需要更多的計算資源時,用戶將從把任務卸載到處理車輛中獲益更多。還發現,隨著用戶數的增加,系統效用也在增加。這是因為,當有許多用戶競爭無線資源和計算資源來卸載他們的任務時,發送任務和在處理車輛上執行任務的開銷會更高,從而降低了卸載效用。從圖中還可以看出,在用戶數相同的情況下,本文所提JDTORA方案與聯合任務卸載和資源分配(joint task offloading and resource allocation, JTORA)方案的系統效用性能極其接近,差值趨于0 。這說明在考慮卸載風險的情況下,即對影響系統卸載的因素考慮更為全面時,系統效用依舊可以趨于不考慮風險的優解,驗證了所提方案的有效性。與傳統的全部本地計算方案進行了比較,本地計算時的卸載效用值為0,因此,當用戶數相同的情況下,本文所提方案的效用大于本地卸載方案的效用。 (a) cn=1 000 圖3(a)~(b)表示當用戶對時間的偏好因子從0.1到0.9變化時,用戶的平均時間消耗和能量消耗變化趨勢。從圖中可以看出,當用戶對時間的偏好α增加時,平均時間消耗降低,相反,平均能量消耗隨之增加。此外,圖中顯示當用戶數更多時,用戶會經歷更大的時間消耗和能量消耗,這是因為當爭奪有限資源的用戶數更多時,用戶從卸載的任務中獲益的機會更小。 (a) 平均時間消耗(a) Average time consumption 圖4顯示的是用戶數與系統風險之間的關系。本文的風險是由于任務卸載引起的,從圖中可以直觀地看出,當任務不進行卸載時(anj=0),系統風險為0;而當用戶數增加時,系統的風險也隨之增大。這是因為當更多的用戶卸載它們的任務時,增大了系統的卸載風險。 圖4 不同工作負載情況下,針對不同用戶數的系統風險比較Fig.4 Comparison of system risks with different numbers of users under different workloads 通過卸載決策和資源分配的聯合優化,設計了邊緣車聯網系統中基于考慮卸載風險的效用最大化問題。優化問題被表述為混合整數非線性規劃問題,此問題是難以解決的,因此將原始問題解耦成兩個子問題,分別使用凸優化技術和分式規劃技術解決。最后,聯合兩個子問題的解在多項式時間內求出了最優的卸載決策。仿真結果表明所提方案在有大量用戶車輛的實際環境中是有效的。 與其他研究不同的是,本文考慮到車輛的移動性,設計了聯合資源分配的動態任務卸載方案,建模了一個風險函數來評估車輛連接中斷的風險。本文的主要貢獻如下: 1)設計了一個邊緣車輛網絡中的動態卸載模型,為了在動態網絡中成功卸載任務,定義了一個風險函數來評估任務卸載失敗的可能性。 2)聯合系統風險定義了一個新的卸載效用函數,并將此問題建模為任務卸載決策、功率分配和計算資源分配的聯合優化問題,以最大化系統的總效用。 3)混合整數非線性規劃問題是難以解決的,通過計算發現,可以將問題解耦成資源分配問題和具有特定解的卸載決策問題。進一步地,將資源分配問題分解為功率分配和計算資源分配,分別使用分式規劃和凸優化技術進行求解。 4)仿真結果表明所提動態卸載方案能夠得到近似最優解,這證明了該方案的有效性。3.2 問題分解
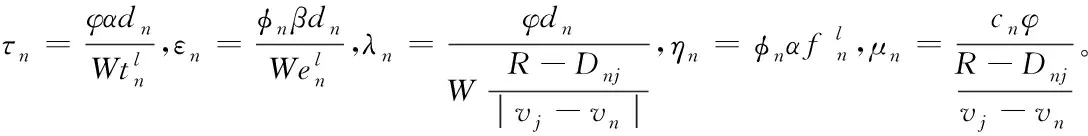
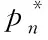
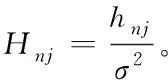
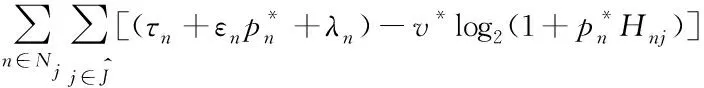
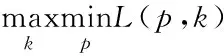
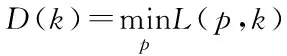



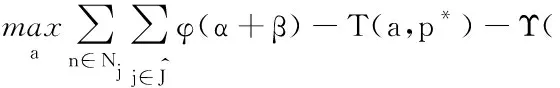

4 仿真分析

5 結論

